一种基于Edwards椭圆曲线的RFID标签芯片加密处理器设计

吴 诚，王俊宇

(复旦大学 专用集成电路与系统国家重点实验室，上海 201203)

一种基于Edwards椭圆曲线的RFID标签芯片加密处理器设计

吴 诚，王俊宇

(复旦大学 专用集成电路与系统国家重点实验室，上海 201203)

本文提出了一款基于二进制Edwards椭圆曲线的高能效椭圆曲线加密处理器．该处理器采用163位密钥，被设计用于无源射频识别(RFID)标签．为了保证椭圆曲线加密(ECC)处理器运算的安全性，处理器使用了二进制Edwards曲线作为加密曲线．ECC处理器中的逻辑运算模块所使用的有限域乘法器基于K-O分治算法进行了优化和设计．验证结果显示，该ECC处理器需要14200个等效门面积，加密过程中完成一次标量乘法需要23023个时钟周期和0.93μJ的能量．该ECC处理器可以满足RFID标签所需要的能耗、时间和面积要求．

射频识别； 椭圆曲线； 二进制Edwards曲线； Karatsuba-Ofman分治算法

射频识别(Radio Frequency Identification, RFID)是一种非接触的自动识别技术．RFID标签具有识别速度快、可嵌入各类非导体包装材质和使用寿命长的特点，已经被广泛用于物流管理、生产管理和电子收费等领域．但随着RFID标签的广泛使用，其安全问题也日益凸显．将RFID标签与非对称密码算法相结合具有加密强度高、难以复制、密钥管理简单等优势．椭圆曲线加密(Elliptic Curve Cryptography, ECC)算法由Miller和Koblitz在1985年第一次提出[1]．同样作为非对称加密算法，ECC相较于传统的RSA加密算法有安全性高和密钥长度短的特点[2]，将其和RFID领域结合有着巨大的应用前景．然而，出于功耗和速度的需求，现存的设计方案需要进行优化才能够被RFID系统所使用．

传统的Weierstrass椭圆曲线被用于加密处理器时存在安全上的问题，如不能抵抗边信道攻击[3]．因此，为了提高系统的稳定性，Edwards椭圆曲线和Hessian椭圆曲线开始被用于加密处理器系统设计[4，5]．本文采用了二进制Edwards椭圆曲线来实现ECC处理器硬件系统，标量乘法采用Montgomery阶梯算法；本设计优化了Karatsuba-Ofman(K-O)算法，将其用于逻辑运算单元(Arithmetic Logic Unit, ALU)有限域乘法运算，从而提高处理器的运算速度．处理器的综合和仿真结果中包括了完成一次标量乘法所需要的时钟数、平均功耗和综合面积．本设计完成了既定的设计指标，证明了在RFID系统中使用Edwards椭圆曲线的可能性．本文还提供了采用4种不同算法的乘法器的仿真结果，可以作为未来研究有限域运算工作的参考．

1 系统分析

1.1 需求分析

一个无源超高频(Ultra High Frequency, UHF)RFID标签是一个工作在860～960MHz的超低功耗设备．无源RFID标签可以通过天线从电磁载波中得到其运行所需要的能量，并通过反向散射的方式与读写器进行通信．无源UHF RFID系统中标签和读写器的距离可以长达30m，在本设计中，我们考虑将该ECC处理器用于物品的快速认证，因此读写器和标签之间的距离不大于20cm．在900MHz的工作频率下，20cm处于近场和远场的过渡区域，我们采用近场模型来模拟标签所能够获得的能量，标签所能获得的能量通过式(1)表示：

Pchip=PreaderρCτ，

(1)

其中的相关参数通过式(2)和式(3)表示[6]：

(2)

(3)

对于900MHz、20cm的应用环境，我们希望标签可以获得至少1mW的能量，1W的读写器可以很容易地提供这样大小的能量．然而考虑到小读写器和标签的情况，我们对实际的环境作保守的估计，假设标签的敏感度是-12dBm，它从1mW的能量中可以得到63μW，如果是符合Gen2协议的标签在没有安全模块的前提下需要大约10μW的能量才能正常工作[7]．因此，加密过程所消耗的能量必须小于53μW．

本设计主要考虑ECC处理器的设计方法，在加密的速度上尽量达到最快，其余部分会着重探讨改善ECC处理器中的有限域乘法器模块，从而达到适合RFID系统的最佳速度．由于面积和乘法器的复杂度呈正相关，也需要尽量降低系统的复杂度，暂定面积小于20000个等效门．我们考虑在面积和功耗符合要求的情况下尽量提高速度的设计方案，最终达到三者的一个平衡．

1.2 曲线选择

Weierstrass椭圆曲线在ECC处理器的设计中早已被广泛使用[8]．然而，Weierstrass曲线存在一些安全问题： (1) 对Weierstrass曲线上的两个数P和Q做加法运算，如果P、Q或者P+Q在无穷远点上，会造成加法运算失败，这被称为不完整性；(2) ECC处理器硬件实现会受到边信道攻击的威胁，因为在Weierstrass曲线上进行的运算是非对称的，通过观察加密过程中的功耗变化，可以用统计的方式得到加密密钥[4]．基于二进制基底的Edwards椭圆曲线可以克服上述缺陷，因为Edwards曲线上的有限域点加和点乘运算具有完备性和统一的计算表达形式，从而给算法本身提供安全保证．

仿射坐标系下的一般Edwards曲线可以用式(4)表示[5]：

E：x2+y2=1+dx2y2.

(4)

如果E(2m)的域由阶2m定义，假设d1和d2是有限域中的元素，并且满足那么Edwards椭圆曲线可以由式(5)来确定[4]：

E：d1(x+y)+d2(x2+y2)=xy+xy(x+y)+x2y2.

(5)

所有Edwards曲线都是非超奇异曲线，且式(5)的曲线与Weierstrass曲线具有双曲线等价性，从而使得Edwards曲线也具有和Weierstrass曲线类型的投影性质．

对于Edwards曲线E(2m)上的点P(x1,y1)和Q(x2,y2)，点加运算P+Q=(x3,y3)满足式(6)：

(6)

从式(6)中可以看出，在该椭圆曲线上，当分母不为0时，相加后的点仍然位于曲线上．并且椭圆曲线上的点加和倍点运算被统一了起来，即当P=Q时式(6)仍然适用，这种性质对于抵抗边信道攻击至关重要．

1.3 算法分析

ω-mix坐标系在数据的存储过程中使用了投影坐标，在计算阶段使用了仿射坐标，这样可以得到简洁的算法实现，在运算过程中节约一次乘法操作的开销．

一种基于二进制Edwards椭圆曲线的简化版Montgomery阶梯算法步骤如下：

1) 输入信号：W1,W2,Z1,Z2；

2) 输出信号：W1,W2,Z1,Z2；

3) 初始化：

4)计算步骤：

Montgomery阶梯算法中进行一次点加和倍点需要6次有限域加法(A)，6次有限域乘法(M)和4次有限域平方(S)运算．因为加法和平方运算仅需要消耗一个时钟周期，可以暂时忽略这两个运算对整体时间消耗的影响，计算时间花费约为6M．这种算法相对于在Weierstrass曲线上进行的运算增加了20%的计算时间(3A+5M+4S)[8]，但是对密码算法来说，安全性的优先级更高．在时间代价下换来的是安全性的提高，因为它可以克服Weierstrass曲线在RFID系统中受到边信道攻击的安全隐患，而Edwards曲线的设计在硬件层面上不会增加太多的面积开销．

1.4 相关工作

表1列出了不同ECC算法和实现的比较结果．这些结果按照曲线的分类、标量乘法方法、坐标系不同等给出了各个方案的优劣总结．为了得到系统性能和消耗之间的平衡，我们选用K-O分治算法来设计系统，并给出不同实现版本之间的比较结果，最后给出系统级仿真结果和性能的比较．

表1 不同椭圆曲线算法的比较

1.5 ECC处理器系统架构

ECC处理器系统架构如图1所示．ECC处理器包括3个主要模块： 有限状态机(Finite State Machine, FSM)模块、ALU模块和寄存器组模块．FSM模块是基于Montgomery算法实现的，按照算法的运算顺序从寄存器组中获得操作数并送入ALU模块进行计算，计算结束后将结果保存起来；ALU模块包括3个基本的有限域运算模块： 加法模块、平方模块和乘法模块．这些有限域运算模块会根据相应的算法完成对应的运算操作，其中的乘法器模块是本设计优化的主要目标，该模块由Alu_in_Mux模块控制，根据状态机来控制ALU模块的输入与输出，使之与正确的寄存器相连；寄存器组模块有5个163位的寄存器构成，负责保存中间的计算结果并在标量乘法完成之后将结果输出给上层的控制模块．下一节会对乘法器模块的实现做具体的分析和讨论．

2 电路实现

该部分主要讨论有限域乘法器的优化实现．除了乘法器以外的加法器、平方器和取模运算由于实现方式简单，可以在文献[18]中找到，本文不再赘述．本设计中的ECC处理器采用的不可约多项式为f(x)=x163+x7+x6+x3+1，在下文的讨论中，用符号(+)来代替异或运算．

乘法操作中假设两个操作数分别为A和B，具体计算方法为： 将A与B的一部分数进行相乘，然后通过移位将B的下一部分进行迭代运算直到结束．对B的移位顺序采用从最高位向最低位进行，也称为最高有效位(Most Significant Bit, MSB)，这样的运算顺序可以加快计算速度[8]．如果在计算过程中，每轮都从B中取出4位与A进行乘法运算直至163位B都计算完毕，这样的串行运算方法会限制ECC处理器的速度．因此，为了达到高速和低功耗的设计要求，可以考虑使用K-O分治算法[17]．当两个处理器拥有相同的运算速度，由K-O分治算法设计的乘法器的功耗增加不及增加相同面积的MSB乘法器的功耗增加，也就是说K-O分治算法乘法器对面积的使用效率更高，这有利于低功耗RFID系统的设计．

K-O算法的分治粒度由一个系数决定，如果系数为2，表示将一个数分成两个部分并送入两个小乘法器分别计算，再将两个结果进行合并处理以得到最终的运算结果．二分治的计算表达式可以用式7表示：

A(z)B(z)= (A1zl+A0)(B1zl+B0)

=A1B1z2l+[(A1+A0)(B1+B0)+A1B1+A0B0]zl+A0B0，

(7)

如果椭圆曲线的不可约多项式为f(x)=x163+x7+x6+x3+1，为了实现对齐，将乘数补为164位，也就是说每个乘法器的位数为82位，这样的分治算法相当于同时有3个82×82的乘法器在进行运算．这样的计算流程需要21个时钟周期来完成一次标量乘法，但最大运算频率将会下降，因为在关键路径上额外增加了3个异或门的延时．二分治乘法器的硬件实现如图2(见第794页)所示．

分治系数为3的模型如图3所示[17]，这需要对两个异或运算模块进行略微修改，且使用了6个55位的乘法器模块．163位向量乘以163位向量的标量乘法可以被分为4个82位乘82位的小乘法器，而每一个82位的乘法器面积约为原来乘法器的面积的一半．所以，最终完成乘法所需要的时钟数减半，而面积会增加两倍．而在K-O算法中，只需要3个82位乘法器，最终造成了1.5倍的面积增长．而如果分治系数设定为3，由于分治算法所产生的系统优势理论上会更大．但是如果电路的复杂度增加，各个模块间的协调和互联所需要的外围电路面积也会成倍的增加．如果将乘法器运算结果进行合并的部分也考虑入系统面积的损耗，实际结果并没有理论上那么大的优势，面积会大于1.5倍的理论值，但仍然小于没有使用分治算法的实现方案．基于以上的分析，分治的系数不能太大，因为需要考虑互联的组合逻辑会随着分治系数的增大而呈现指数增长的趋势．相关研究中已经证明，分治的系数不应该超过4[17]．

为了减少更多功耗，本设计实现了一款二分治的双周期锁存的乘法器模块．如图4所示，这个实现是基于使用面积来减少功耗的想法．这个实现中的能耗主要来源于寄存器的锁存周期，所以如果降低将数据存入寄存器的频率，应该就可以起到减少功耗的作用．该乘法器分为奇偶两个部分，奇偶部分不会同时工作．在一个特定的时钟周期内，该电路只有一半会参与运算过程，因此理论上来说，这样的设计能将功耗减半．下一部分会对以上几种乘法器架构设计给出一个验证结果．

3 系统验证

该部分验证4种类型的乘法器设计．综合工具为Synopsys公司的Design Complier，综合频率为1MHz．结果如表2所示，比较对象是没有进行任何分治的系统，也就是分治系数为1的乘法器设计方案．根据表2绘制的数据关系图如图5所示，图中将数据进行了归一化处理，也就是将所有的数据都转换到0～70的数字范围内，从而可以在一张图中看出各组数据之间的关系．

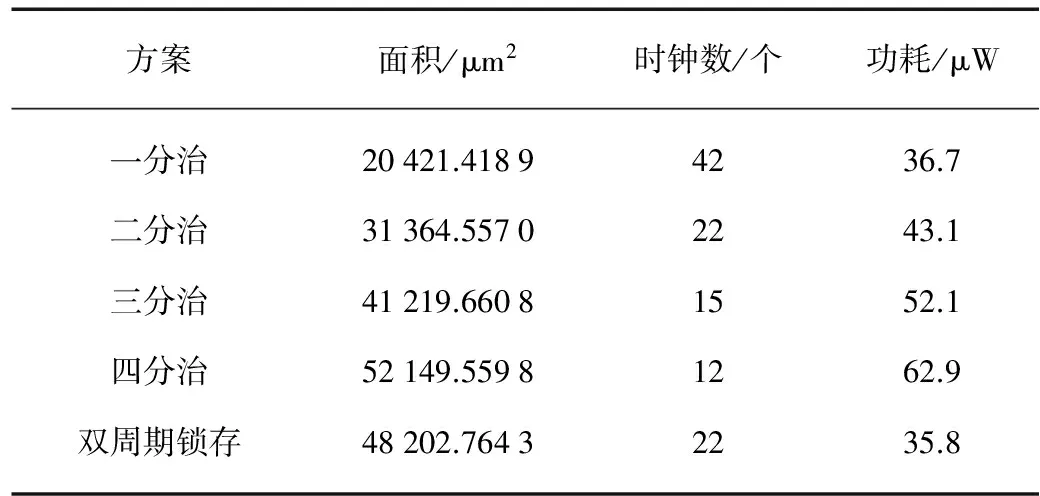
方案面积/μm2时钟数/个功耗/μW一分治20421．41894236．7二分治31364．55702243．1三分治41219．66081552．1四分治52149．55981262．9双周期锁存48202．76432235．8

从表2可以看出，当分治系数变为原来的k倍时，所需要的周期数也按照k倍降低．面积的计算方式如式8所示：

(8)

式中m代表了理论上的面积大小，n是分治系数，从中可以看出m与n基本成线性关系．然而功耗增长的速度远远大于分治系数增长的幅度，这主要是由于组合逻辑电路面积随分治系数增大快速增长的原因．从中可以看出对应于RFID应用，分治系数为2～4是比较合理的．

另外，双周期锁存实际上的优化效果并不是很明显，虽然功耗有一定的下降，但是面积存在大幅增长，对比二分治算法，面积增大了53%．这需要我们考虑这种折中权衡的合理性，当然如果对面积的要求并不严格，或者能更好地简化双周期锁存中的逻辑运算操作，该方案或许有一定的可行性．最终的乘法器和ECC处理器验证结果如图6所示．

对于Edwards椭圆曲线来说，二分治的版本加密一位需要的时钟数为6×22+4×1+4×1+2×1=142，所以对于m位的密钥需要142×m的时钟数来完成标量乘法；如果分治系数为3，需要的时钟数为T=(6×15+4×1+4×1+2×1)×(m-1)+28≈100×m．分治算法对于提高运算速度有着显著的效果．如果时钟频率设为1MHz，二分治系统需要22.86ms来完成一次ECC标量乘法操作，三分治仅需要16.1ms来完成．这样的运算速度与文献[8]中说明的系统指标相适应．

考虑到我们设计的系统功耗不宜太大，且需要将面积控制在一定范围以内，二分治乘法器构成的系统应该是最适合RFID应用的．二分治的系统综合结果如表3所示．从表中可以看出，乘法器所占的面积和功耗都是整个ECC处理器中最大的，所以设计目标着重点放在乘法器上是合理的．另一方面，也说明了双周期锁存设计存在一定的合理性，也就说用更大的面积换取功耗的降低，在面积不是主要考虑因素的场合是可以考虑使用的．如果想要进一步减少面积从而达到节约成本的效果，可以考虑增加乘法器的复用，即仅使用一组小乘法器进行计算，而将中间的计算结果保存在寄存器中，然后进行第二部分运算，待两部分运算结束之后，再计算最终结果．这样的方法是用速度来换取面积，可以在面积是约束条件的设计要求中使用．此外，寄存器模块虽然面积比较大，但是功耗却比较小的原因是我们采用了门控时钟和操作数隔离的方法使得运算过程中只有在需要数据被存回寄存器模块时该模块的时钟才会接通，不工作时处于关断状态，尽最大可能减少了静态功耗．

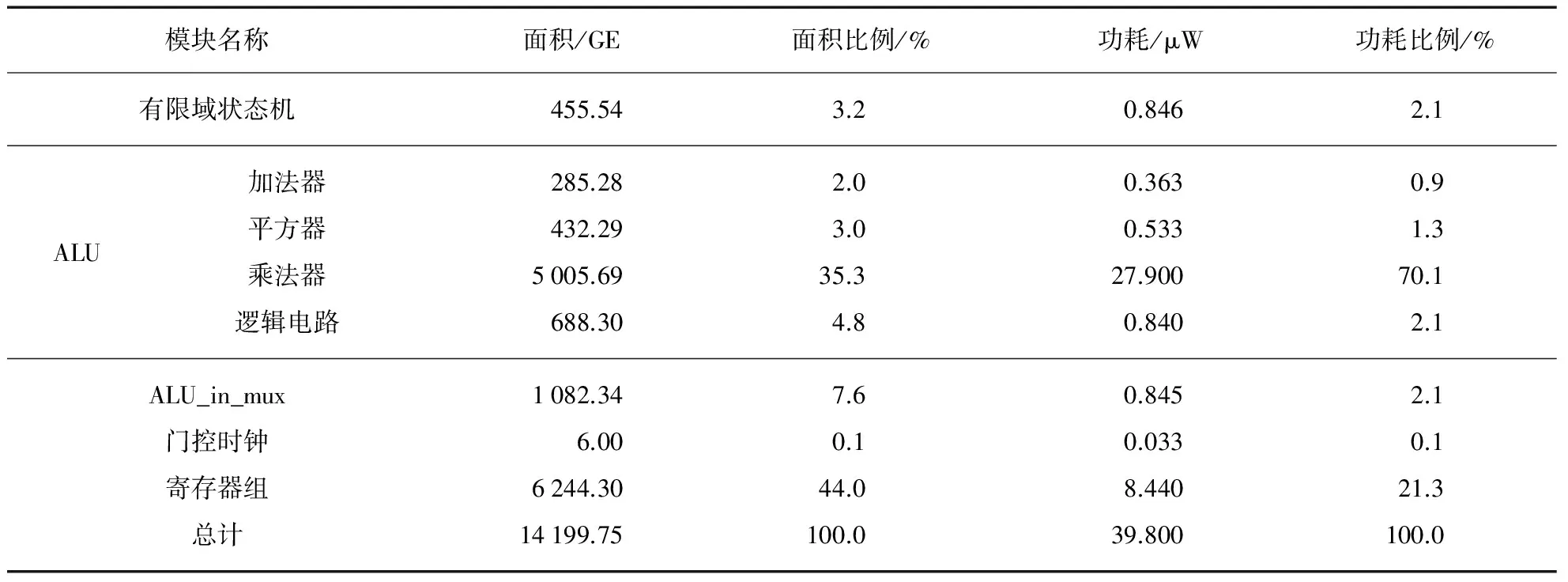
表3 二分治乘法器ECC处理器综合结果

包含二分治乘法器的ECC处理器与其他文献的对比结果如表4所示．

表4 基于Edwards椭圆曲线ECC处理器性能比较

由于参考文献中的设计是在不同的工艺和频率下综合实现的，为了进行公平的比较，本文考虑采用在加密一次所需要的能量，也就是在能效的尺度上进行比较．各个椭圆曲线加密处理器可以通过比较能量利用率而不是加密的时间或者加密的功耗来避免时间和综合频率不同所造成的差别．从表中可以看出我们的设计面积稍大，但由于使用了K-O算法，所消耗的能量远远小于其他的设计，功耗的大小也符合我们在第1节需求分析中所规定的指标，这使得该设计可以被用于RFID的实际应用中去．

4 结 语

本文提出了一款基于二进制Edwards椭圆曲线的高性能ECC处理器．处理器实现过程中使用了K-O分治算法，用于实现标量乘法中的有限域乘法运算．本设计的面积为14200个等效门，在1MHz的工作频率下，完成一次标量乘法需要0.93μJ，所需要的时间为22.86ms，该ECC处理器的设计是面积、速度和功耗的权衡取舍，最终的硬件实现方案能满足RFID的应用需求．

[1] MILLER V S. Use of elliptic curves in cryptography[C]∥Advances in Cryptology-CRYPTO’85 Proceedings. Berlin-Heidelberg： Springer, 1985： 417-426.

[2] HEIN D, WOLKERSTORFER J, FELBER N. ECC is Ready for RFID-A Proof in Silicon[C]∥Selected Areas in Cryptography. Berlin-Heidelberg： Springer, 2008： 401-413.

[3] IZU T, TAKAGI T. Exceptional procedure attack on elliptic curve cryptosystems[M]∥Public Key Cryptography-PKC 2003. Berlin-Heidelberg： Springer, 2003： 224-239.

[4] BERNSTEIN D J, LANGE T, FARASHAHI R R. Binary edwards curves[M]∥Cryptographic Hardware and Embedded Systems-CHES 2008. Berlin-Heidelberg： Springer, 2008： 244-265.

[5] QI Y, XU M, TANG C. A class of elliptic curves in edwards form[C]∥Conference Anthology, IEEE. Shanghai, China, IEEE press, 2013： 1-4.

[6] NIKITIN P V, RAO K V S, LAZAR S. An overview of near field UHF RFID[C]∥IEEE international Conference on RFID, 2007: 167.

[7] ZHOU F, CHEN C, JIN D,etal. Evaluating and optimizing power consumption of anti-collision protocols for applications in RFID systems[C]∥Proceedings of the 2004 international symposium on Low power electronics and design. Newport Beach, CA, USA, 2004： 357-362.

[8] LEE Y K, SAKIYAMA K, BATINA L,etal. Elliptic-curve-based security processor for RFID[J].IEEETransactionsonComputers, 2008,57(11)： 1514-1527.

[9] AL-DAOUD E, MAHMOD R, RUSHDAN M,etal. A new addition formula for elliptic curves over GF (2n)[J]. IEEE Transactions on Computers, 2002,51(8)： 972-975.

[10] LIM C H, LEE P J. More flexible exponentiation with precomputation[C]∥Advances in cryptology-CRYPTO’94. Berlin-Heidelberg： Springer, 1994： 95-107.

[11] LONGA P, MIRI A. New composite operations and precomputation scheme for elliptic curve cryptosystems over prime fields[M]∥Public Key Cryptography-PKC 2008. Berlin-Heidelberg： Springer, 2008： 229-247.

[12] DIMITROV V, IMBERT L, MISHRA P. The double-base number system and its application to elliptic curve cryptography[J].MathematicsofComputation, 2008,77(262)： 1075-1104.

[13] MENEZES A J, VAN OORSCHOT P C, VANSTONE S A. Handbook of applied cryptography[M]. FL Boca Raton, USA： CRC press, 1996.

[14] KOCHER P C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems[C]∥Advances in Cryptology-CRYPTO’96. Berlin-Heidelberg： Springer, 1996： 104-113.

[15] AZARDERAKHSH R, REYHANI-MASOLEH A. Parallel and high-speed computations of elliptic curve cryptography using hybrid-double multipliers[J].IEEETransactionsonParallelandDistributedSystems, 2015,26(6)： 1668-1677.

[16] KIM C H, HONG C P, KWON S. A digit-serial multiplier for finite field GF (2m)[J].IEEETransactionsonVeryLargeScaleIntegrationSystems, 2005,13(4)： 476-483.

[17] KARATSUBA A A. The complexity of computations[J].ProceedingsoftheSteklovInstituteofMathematics-InterperiodicaTranslation, 1995,211： 169-183.

[18] KOCABAS Ü, FAN J, VERBAUWHEDE I. Implementation of binary Edwards curves for very-constrained devices[C]∥21st IEEE International Conference on Application-specific Systems Architectures and Processors (ASAP), 2010. Rennes, FRANCE： IEEE Press, 2010： 185-191.

[19] LIU D, LIU Z, YONG Z,etal. Design and Implementation of An ECC-Based Digital Baseband Controller for RFID Tag Chip[J].IEEETransactionsonIndustrialElectronics, 2015,62(7)： 4365-4373.

An ECC Processor Based on Edwards Curve for RFID Tag

WU Cheng, Wang Junyu

(StateKeyLaboratoryofASIC&Systems,FudanUniversity,Shanghai201203,China)

In this paper, we propose an energy-efficient 163-bit elliptic curve cryptographic(ECC) crypto processor for passive radio frequency identification(RFID) tags. The encryption curve used for this processor is binary Edwards curve. The multiplication of arithmetic logic unit(ALU) in ECC processor is optimized and implemented with the Karatsuba-Ofman conquer and rule algorithm. According to the verification results, the ECC processor requires 14200 equivalent gates area and 23023 cycles with 0.93J energy consumption for one scalar multiplication encryption process. The ECC processor can meet the power, area and timing requirements of RFID applications.

Radio Frequency Identification(RFID); Elliptical Curve Cryptography(ECC); binary Edwards curve; Karatsuba-Ofman algorithm

0427-7104(2016)06-0790-09

2016-05-30

国家科学技术支柱计划(2015BAK36B01)；国家自然科学基金(61076022, 61211140046)

吴 诚(1989—)，男，硕士研究生；王俊宇，男，教授，通讯联系人，E-mail： junyuwang@fudan.edu.cn.

TN 4

A