矩阵的体积及其在积分变换中的应用
张磊
(1.安徽师范大学 数学与计算机学院,安徽 芜湖 241003;2.阜南会龙中心校,安徽 阜阳 236300)
矩阵的体积及其在积分变换中的应用
张磊
(1.安徽师范大学 数学与计算机学院,安徽 芜湖 241003;2.阜南会龙中心校,安徽 阜阳 236300)
本文首先给出了一般矩阵体积的概念和性质并用一些例子具体介绍矩阵体积的求法,重点探讨了矩阵体积在定积分、重积分、曲线积分和曲面积分中的应用。
长方矩阵;矩阵体积;雅可比矩阵;积分
在介绍本文之前,先介绍一些知识
Qr×n={I={i1,i2,…,ir}:1≤i1<i2<…<ir≤n}表示{1,2,…,n}中依次增加的r个数的集合
I(A)={I∈Qrxn:rank(AI*)=r}表示A中最大的线性无关的行指标数
J(A)={J∈Qr×m:rank(A*J)=r}表示A中最大的线性无关的列指标数
N(A)={(I,J)∈Qr×n×Qr×m:rank(A)=r}表示A中最大的非退化矩阵的集合的行与列指标数,则N(A)=I(A)×J(A),可以简写为I×J=N

1 矩阵的体积
对于任一n阶方阵A,可以定义其行列式detA=|A|,但对于长方矩阵不能定义其行列式,为此引出新的概念——矩阵的体积。
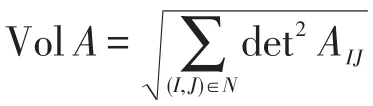
性质1[4]:A∈Rn×m,r>0,A的一个满秩分解A=BD,(B∈,D∈),则

性质2[4]:若A∈,r>0,且r≤n,A是列满秩的矩阵,则。
性质3[4]:若A∈,r>0,且r≤m,A是行满秩的矩阵,则。
以下用几个例子来熟悉矩阵体积的计算:

2 积分体积在积分变换中的应用
设u,v∈Rn,Φ:u→v连续可微的函数,并且f是v上的可积的函数,则有
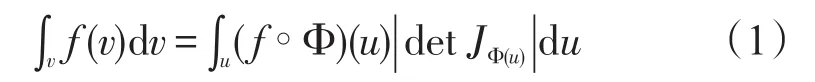
则称JΦ(u)为雅可比矩阵,|detJΦ(u)|雅可比行列式(即雅可比矩阵的体积)。从上面(1)式知,数学分析中在求定积分,重积分,曲线积分与曲面积分中,有时经过变换Φ,使得在解决问题时过程简单,计算方便,在这简化运算时,通过雅可比矩阵来实现的。
以下分别从定积分,重积分,曲线积分和曲面积分来考察矩阵的体积在积分变换中的应用。
2.1 矩阵体积在定积分中的应用
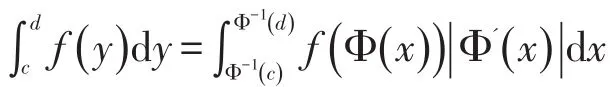
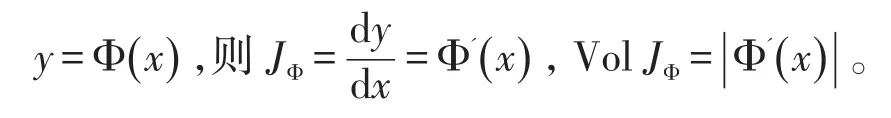
例3设y=,2≤y≤3,变换成x的积分并且求出体积。
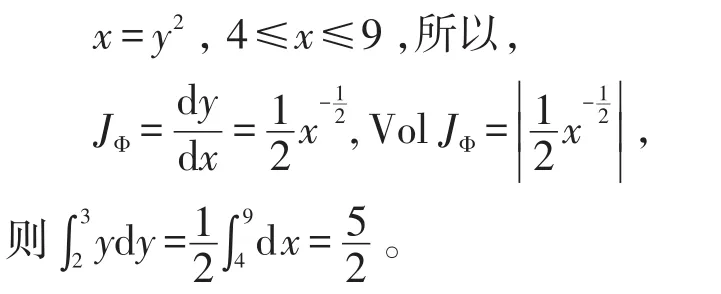
解由题意得2.2 矩阵体积在重积分中的应用

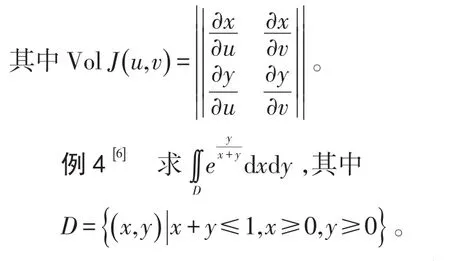


同时,D变成了D'={(u,v)|0≤v≤1,0≤u≤v},如图2。
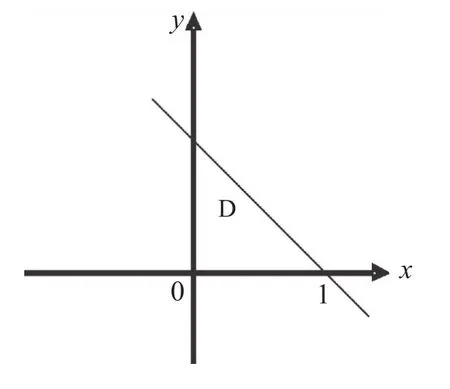
图1 例4中的区域D

图2 例4中的区域D'

2.3 矩阵体积在曲线积分中的应用


2.4 矩阵体积在曲面积分中的应用
定理4设有光滑曲面S:z=z(x,y),(x,y)∈D,f(x,y,z)为S上的连续函数,



图3 例7中的区域D
解由题意得


3 结论
矩阵的体积是矩阵行列式的推广,本文根据矩阵的秩与行(或列)数来介绍矩阵体积的求法,并通过例题来说明矩阵的体积在定积分,重积分,曲线积分,曲面积分等积分变换中的应用。
[1]陈荣群,张锦州,金秀玲.矩阵体积的一个基本性质[J].闽江学院学报,2008,29(5):5-8.
[2]李 明,方 宜.矩阵的体积及其应用.[J]西北师范大学学报(自然科学版),2005,41(6):86-90.
[3]陈绍木,陈清华,王华雄,等.高等代数[M].2版.福州:福州教育出版社,1992.
[4]陈荣群,张锦州.矩阵的体积与初等变换.三明学院学报[J].2011,28,2,23-27。
[5]华东师范大学数学系.数学分析第三版[M].4版.北京:高等教育出版社,2003.
[6]钱吉林等.数学分析题解精粹第二版[M].湖北长江出版集团,武汉,第一版,2006年.
[7]陈纪修,於崇华.数学分析第二版[M].2版.北京:高等教育出版社,2004.
[8]裴礼文.数学分析中的典型问题与方法[M].2版.北京:高等教育出版社,2002.
[9]Ben-Israel and N.E.Greville.Generalized Inverse:Theory and Applications[M].second Edition,New York, springer velag.2003
[10]Ben-Israel.A volume associated with mn matrices[J]. LinearAlgebra and itsApplication.167(1992),87-111
The volume of the matrix and its application in integral transformation
ZHANG Lei
(1.School of Mathematics and Computer,Anhui Normal University,Wuhu Anhui241003,China;2.Huilong Center School of Funan,Fuyang Anhui236300,China)
In this paper,the concept and properties of the general matrices’volume were first given,then some examples are introduced to calculate the matrix volume.The applications of the matrices’volume in definite integral,heavy integral, curve integral and surface integral are discussed in details.
matrix;volume of matrix;Jacobi determinant;integral
O175.12
:A
:1004-4329(2016)04-019-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)04-019-04
2016-09-20
张 磊(1972- ),男,硕士生,研究方向:中小学数学教育。

