要素误置给中国农业带来多大损失？——基于超越对数生产函数的随机前沿模型

程丽雯，徐 晔，陶长琪

（江西财经大学统计学院，江西南昌330013）

要素误置给中国农业带来多大损失？
——基于超越对数生产函数的随机前沿模型

程丽雯，徐 晔，陶长琪

（江西财经大学统计学院，江西南昌330013）

在Aoki（2012）的理论框架上纳入了农业最主要的投入要素——土地，同时建立超越对数生产函数的随机前沿模型进行系数估计，通过对产出变动的再分解，从理论和实证两个方面验证了要素误置对农业生产的抑制作用，弥补了C-D生产函数无法考虑要素间扭曲相互作用的不足。结果表明：第一，农业要素存在误置现象。对比各要素间的扭曲程度，土地要素扭曲最为严重；对比各地区间的要素误置程度，中部地区农业要素误置最为严重。第二，农业要素误置带来产出损失。通过对要素扭曲效应再分解，发现各要素间价格扭曲相互作用带来的产出损失大于要素自身价格扭曲带来的产出损失。实证研究表明，用超越对数生产函数替代C-D生产函数进行要素误置的分析更加合理。

农业投入；资源错配；农业经济；价格扭曲；超越对数生产函数

引言

“三农”问题一直是我国社会主义现代化建设的关键问题。虽然近年来农业比重在下降、农村人口在减少，但农业在国民经济中的基础地位仍旧没有改变。现阶段，实现全面建成小康社会宏伟目标，农业农村发展越来越重要。农业农村的发展不仅取决于农业技术水平的提高，而且取决于农业要素的优化配置及利用效率的提高，正如Johnson（1997）［1］曾指出的，对于中国这样的发展中国家而言，农业全要素生产率（TFP）的增长是国民财富增长的核心。

中国农业投入要素及其配置与农业产出问题一直受到学者的广泛关注。国外学者Wiens（1982）［2］、McMillan（1989）［3］、Fan（1991）［4］、Lin（1992）［5］等最早对中国农业全要素生产率进行了研究，他们普遍认为我国农业全要素生产率在改革开放初期具有较高增速，而在计划经济时期处于停滞状态。我国学者杨刚（2013）［6］、彭代彦（2013）［7］、潘丹（2013）［8］、应瑞瑶（2012）［9］等用不同方法对农业全要素生产率进行分析，考察了基于不同视角农业全要素生产率的变化趋势和空间相关性。

直到2009年，Hsieh&Klenow［10］发现，由于要素价格扭曲的存在，资源配置无法达到最优。同时，他们的研究表明，若对中国的劳动及资本进行重新配置，TFP将提高25%～40%。于是，要素价格扭曲对产出影响的研究逐渐引起人们的重视。例如，Aoki（2012）［11］、陈永伟（2011）［12］通过对产出变动进行分解，从理论和实证角度讨论了要素价格扭曲对制造业产出的影响，发现要素错配对制造业的影响主要体现在中间投入品价格扭曲上；曹东坡（2014）［13］则对服务业要素错配现象进行研究，发现服务业要素错配对服务业的影响逐年增大且存在较大地区差异，错配的要素主要为劳动价格扭曲。

对农业要素错配进行讨论的文献并不多见。朱喜（2011）［14］在未考虑土地投入要素的情况下通过构建C-D产出函数，讨论了要素配置扭曲程度及其与TFP之间的关系，发现农业要素误置存在严重的地区差异。但由于模型限制，他无法量化资本和劳动错配程度对产出变动的影响。而Assuncao（2003）［15］、李谷成（2009）［16］和Adamopoulos（2013）［17］则仅对土地投入要素扭曲对产出的影响进行讨论，未对劳动和资本的扭曲问题展开研究。他们认为土地规模变化会造成农业生产效率损失，而发展中国家的政策干预是土地规模扭曲的主要原因。

可以看出，现有文献对农业要素误置方面的研究仍旧存在很大缺陷。基于此，本文将要素错配定义为要素边际产出在各经济个体层面上不相等的现象，并通过“价格税”对农业生产中的三大主要投入要素——资本、土地、劳动力的误置进行量化研究，构建不再具有产出弹性固定强假设的超越对数生产函数，结合中国农业要素价格扭曲现状和Aoki（2012）［11］的带有扭曲的竞争均衡模型，在测算相对扭曲系数的基础上对产出变动进行分解，讨论产出变动和再分解后要素扭曲效应的影响因素。结果表明：通过要素扭曲效应反映的要素误置对农业产出有负效应；经再分解表明：要素间相互作用对要素价格扭曲的影响不容忽视，各要素间价格扭曲相互作用带来的产出损失大于要素自身价格扭曲带来的产出损失。

本文在综合考虑已有研究的基础上做出以下改进：第一，纳入农业主要投入要素——土地，探讨土地要素误置对中国农业要素市场扭曲的影响问题；第二，用超越对数生产函数替代C-D生产函数，探讨要素价格扭曲相互作用对产出影响的不可忽视性，弥补C-D生产函数无法考虑要素间扭曲相互作用的不足，保证结果的准确性和合理性；第三，用超越对数生产函数的随机前沿模型实现产出的分解，探讨技术进步对产出贡献的可分解性。

一、理论模型

（一）N个地区的竞争均衡

假设有N个地区生产同样的农产品，且产品市场是完全竞争的，所有农户都是农产品价格的接受者，所有农户都投入三种要素进行生产：劳动L、资本K和土地M。基于农业无特定行业划分的特殊性和农户个体数据的不可得性，假定同一地区所有农户的生产函数均相同，因此可以用一个农户的生产函数来代表该地区的生产函数。区别于发达国家的诱导型经济体制，中国的政府主导型经济体制主要依赖国家政策促进经济发展，造成了严重的要素价格非市场化现象。畸形的要素比价关系必然扭曲要素投入结构，故用假设要素规模报酬不变来测算出的各投入要素的产出弹性难免被高估。基于以上考虑，与Aoki（2012）［11］、陈永伟（2011）［12］、朱喜（2011）［14］采用C-D生产函数研究要素误置问题不同，本文采用易估计和包容性很强的超越对数生产函数进行研究。一方面，它允许替代弹性随要素密集度变化而变化，另一方面，它能有效反映多要素投入下的最小投入需求以及任意要素间的相互作用关系，因而更适合多要素投入下的要素产出弹性的全局动态分析。考虑i个地区的农业投入要素——劳动、资本和土地，可以得到第i个地区的生产函数表达式如下：

为了使每个地区达到竞争均衡，首先构建地区i的利润函数

根据利润最大化目标，得到一阶最优条件：

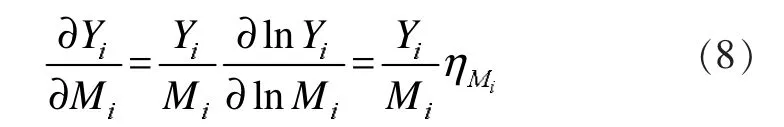
其次，对i个地区（作为经济体S）的加总生产函数进行定义，假设该加总生产函数规模报酬不变（CRS），且满足

根据欧拉定理，有

最后，假定整个经济体S各项投入要素的供给总量是外生给定的，由此可以构建资源约束条件：

结合式（1）至式（13），我们可以定义该经济总体在要素市场价格扭曲下的竞争均衡。如同Aoki（2012）的研究一样，给定全要素生产率（AI）、投入要素的“价格税”和投入要素的供给总量（K、L、 M），在满足式（1）至式（13）的条件下，可以得到一个由组成的竞争均衡。

利用这个竞争均衡，我们可以导出用“价格税”表示的地区i的各项要素投入量Ki、Li、Mi。联立式（2）、式（6）、式（10）和式（11），得到Ki的表达式

同时，根据Hsieh&Klenow（2009）［10］研究中关于相对扭曲系数和绝对扭曲系数的定义，我们记资本的绝对扭曲系数为

记资本的相对扭曲系数为

联立式（14）、式（15）和式（17），可以得到

式（17）至式（20）揭示了扭曲的“价格税”对投入要素（资本、劳动和土地）配置所产生的影响。

首先，从式（18）和式（19）可以看出，“价格税”主要通过相对扭曲系数影响各经济个体的要素配置，同时也可以通过各地区产出的市场份额作用于要素配置。值得注意的是，此处要素产出弹性［见式（5）］不但包括C-D生产函数中生产要素对经济增长的直接效应，而且还包含了各要素相互作用引起的产出外溢效应。要素配置的另一个重要影响因素——要素溢出效应的提出，说明超越对数生产函数中的要素产出弹性放松了C-D生产函数形式中要素相互作用无产出贡献这一强假设。因此“价格税”也可以通过要素之间的溢出效应作用于要素配置，这是以往各类研究从未涉及的。

其次，由式（17）可知，相对扭曲系数是地区i在要素误置条件下所获得回报 （即高于无扭曲时的价格的部分，也有可能是亏损）的倒数与所有N个地区在相同条件下所获得回报的加权平均值的倒数形成的比率关系，它体现了地区i相对于总体平均值的资源扭曲情况。当N个地区的“价格税”相同时，所有个体同种要素的相对扭曲系数均相同，这意味着在这个经济体S中，任意地区i不存在要素价格扭曲即要素误置情况。当N个地区间的“价格税”分布情况不同，如（地区i的“价格税”小于N个地区的平均“价格税”）且每个地区产出的市场份额差异不大、要素溢出效应不明显时，地区i的资本要素投入会大于不存在要素误置的情形。若考虑“价格税”不同使得每个地区产出的市场份额分布和要素溢出效应各不相同的情形，则要通过它们之间作用大小的对比来分析要素误置。

最后，式（20）反映了相对扭曲系数的另一层含义，即它还是要素市场扭曲条件下地区i的要素配置与要素对产出的贡献率所构成的比率关系，这说明了要素市场扭曲状况是基于地区间“价格税”分布各不相同而产生且相对于整个经济体的平均水平而言的，验证了用相对扭曲系数而非直接采用绝对扭曲系数的必要性。另外，若相对扭曲系数大于1，表明要素成本过高，地区i“价格税”主要通过要素市场相对扭曲系数影响要素配置；若相对扭曲系数接近于0，则表明要素成本过低，“价格税”主要通过产出的市场份额分布和要素溢出效应影响要素配置。

（二）产出变动的分解

为了研究不同时期的产出变动情况，将时间趋势纳入生产函数，建立资本、劳动和土地三要素的超越对数生产函数的随机前沿模型［18-19］，则式（1）变为

对时间t求偏导，根据中值定理，由t时刻到t+1时刻的产出变动（为了简便，省略it脚标）为

根据式（18）、式（19）、式（21）和式（22），可得产出变动表达式（仅省略i脚标）如下：

由式（23）可知，产出变动分成五部分：

第一部分是技术进步（TP），它反映了在投入要素不变的情况下，产出随时间变化的变化率。它由中性技术进步贡献率（TP中的前两项）和偏向性技术进步率（TP中的后三项）两部分组成，其中偏向性技术进步率是随时间和要素禀赋变化的配置效率因子。当TP>0时，表示技术进步；当TP<0时，表示技术退步；当TP=0时，表示技术保持不变。

第二部分是技术效率的变化（TE）。根据随机前沿函数可知，是相对于时间的变化率。TE>0，表示技术效率提高；TE<0，表示技术效率降低；TE=0，表示技术效率不变。

第三部分是地区市场份额在不同时期的变化对产出变动的贡献，记作SS。其中，反映了规模报酬变化情况，，表明从第t年到第t+1年该地区呈规模报酬递增，分别反映规模报酬递减和规模报酬不变。

第四部分是要素扭曲效应（DE），表示要素投入在不同时期的配置结构变化对产出变动产生的影响。通过该指标可以分析要素价格扭曲对产出变化的贡献。这里验证了式（18）和式（19）的正确性，“价格税”主要通过相对扭曲系数影响各地区的要素配置，而DE进一步反映了这种影响机制对产量变动的影响。

第五部分是要素贡献加权比率的变化 （CE）。在C-D生产函数中，不同时期的要素贡献值往往是固定值，而在放宽了假设条件的超越对数生产函数中，要素贡献值随着时间和地域的变化而变化。要素贡献加权比率的变化不仅可以衡量在要素误置下的要素贡献率对产出的影响，而且可以通过具体数据对放宽C-D生产函数假设的必要性进行论证。

（三）要素扭曲效应（DE）的影响因素分析

为了深入了解要素误置对产出的影响，本文重点考虑的分解项是要素扭曲效应（DE）。

由式（23），可把要素配置效应再分解为各个投入要素配置对产出的影响，如下式所示：

其中DEK、DEL和DEM分别为投入要素资本、劳动和土地所产生的市场扭曲程度变动对产出变动的影响。

由于加入了时间变量，根据式（21），投入要素K的产出弹性变为

可以看出，投入要素K的产出弹性与C-D生产函数中的固定性强假设不同，它不仅包含了生产要素对经济增长的直接效应，而且还包含了K与L、K与技术进步之间相互作用以及K自身对产出增加的溢出效应。因此，DEK主要取决于相对扭曲系数，同时还受投入要素K的产出弹性影响，而这种影响包括直接效应和溢出效应两方面的作用。这再一次验证了式（18）和式（19）的正确性，反映了扭曲的“价格税”通过要素产出弹性的直接效应和溢出效应对投入要素（资本、劳动和土地）配置所产生的影响，而对DE再分解进一步反映了这种影响机制对产量变动的影响，如下式所示：

其中DDEK表示直接效应下资本要素价格扭曲对产出变动的影响，ODEK表示溢出效应下资本要素价格扭曲对产出变动的影响。

目前大多数研究都是围绕直接效应下的要素误置展开的，但单个经济变量的要素误置情况的变化会带来其他经济变量的相应变化，特别是在要素投入中，一种要素投入的减少往往伴随着另一种要素投入的增加，以保证成本最小化下的经济持续增长。所以本文借助超越对数成本函数的随机前沿模型对要素误置下的产出变动进行分解，相比以往的研究，这种方法更加合理和严谨。

类似式（26），可以导出劳动和土地这两种投入要素误置对产出变动的影响，如下式所示：

二、模型估计与检验

根据理论模型，为了测算各地区的相对扭曲系数，本小节将运用最大似然回归对构建的超越对数生产函数的随机前沿模型即表达式（21）中的投入要素产出弹性进行估计，并从模型的设定检验和稳健性检验两方面验证模型和实证结果的可靠性。

（一）数据说明

本文讨论的是30个省、自治区、直辖市2000—2012年的农业生产过程（由于西藏自治区数据缺失过多，故做剔除处理）。需要说明的是，为了保证与农业投入（劳动力、资本、土地）统计口径相一致，本文不考虑存在相关副业的农业，只考虑包括农林牧渔四大产业的农业。这与李谷成（2009）［20］、郭军华（2010）［21］等的处理方式是一致的。

根据数据的可得性和合理性，刻画各变量的指标选择如下：

第一，资本投入量。本文用永续盘存法（PLA）估算的农业资本存量表示资本要素。

计算农业资本存量，涉及基期资本存量、各期资本投入增量、资产价格指数和资本折旧率等数据。以2000年为基期，借鉴Young（2000）［22］所采取的折旧-贴现法确定基年资本存量，选取折旧率δ=6%，将基年投资除以投资平均增长率与折旧率之和得到的商作为基期资本存量。根据李宾（2011）［23］的研究，采取各地固定资产形成额或全社会固定资产投资额作为各期资本投入增量，二者所计算的资本存量差距不大，所以，本文把从《中国统计年鉴》和《中国固定资产投资统计年鉴》中得到的农林牧渔业固定资产投资总额作为2000—2012年的资本投入增量，单位为亿元。由于各期资本投入增量是以当年价格计算的，为了平减为2000年不变价格，与蔡晓陈（2009）［24］一样，本文用各省固定资产投资价格指数（也需要换算为2000年不变价格）作为资产价格平减指数，使固定资产投资总额变为2000年不变价格，数据来自《中国城市生活与价格年鉴》和《中国统计摘要2013》。综上所述，资本存量的计算公式如下：

利用式（29），可以计算得到农业的资本存量。

第二，劳动力投入量。用第一产业就业人员数量表示农业劳动力要素［7-8］，单位为万人。

2000—2009年数据可以从《中国统计年鉴》中得到，而2010—2012年数据来自各省统计年鉴。针对黑龙江省2011年和2012年数据缺失的情况，本文采用相似省份数据补充的方式，以甘肃省2011年和2012年的数据代替。

第三，土地投入量。在狭义农业的定义下，土地投入即农作物播种面积［8，9，25］。本文所讨论的农业包括农林牧渔四大产业，土地投入不仅包括用作耕地的土地，还包括非用作耕地的土地。根据数据的可得性，我们采用农作物播种面积、造林面积和水产养殖面积的加总来表示土地投入量，单位为千公顷。其中，农作物播种面积和造林面积可直接在《中国农业统计年鉴》中得到，水产养殖面积用淡水养殖面积（或内陆养殖面积）与海水养殖面积加总得到。

第四，农业产出量。以农林牧渔业产出增加值表示［13］，单位为亿元，数据来自《中国农业统计年鉴》。由于农业产出增加值均是按当年价格计算的，所以用GDP价格指数平减为2000年不变价格，以保证数据的准确性和合理性。

（二）模型估计及结果分析

根据理论模型，为了测算各地区的要素误置情况，这一部分要对随机前沿模型式（21）进行参数估计。

最早对随机前沿模型进行参数估计的方法是两步回归法，但是这种方法要加入两个假设条件：第一，假定无关效率项的外生解释变量与投入要素间不存在相关性；第二，用来解释技术变量的外生变量往往在第一步回归时被假定为与技术效率无关的变量。显然，这些假定条件造成了第一步回归和第二步回归的内在冲突，违背了无效率部分同分布假定。所以，经过对模型进行改进，Battese（1995）［26］提出了可以对随机前沿模型参数采用一步极大似然法进行估计。这种方法放宽了两步回归法中的同分布假定，克服了两步回归法的理论矛盾，目前，它的可靠性和优越性已经得到了学者们的证实。因此，本文使用Frontier4.1对生产函数表达式（21）采用一步回归法进行估计。为了对生产效率方程进行解释，加入表示地区差异的地区虚拟变量作为生产效率方程中的外生解释变量，得到生产效率方程。其中：

采用一步回归法估计的结果见表1。

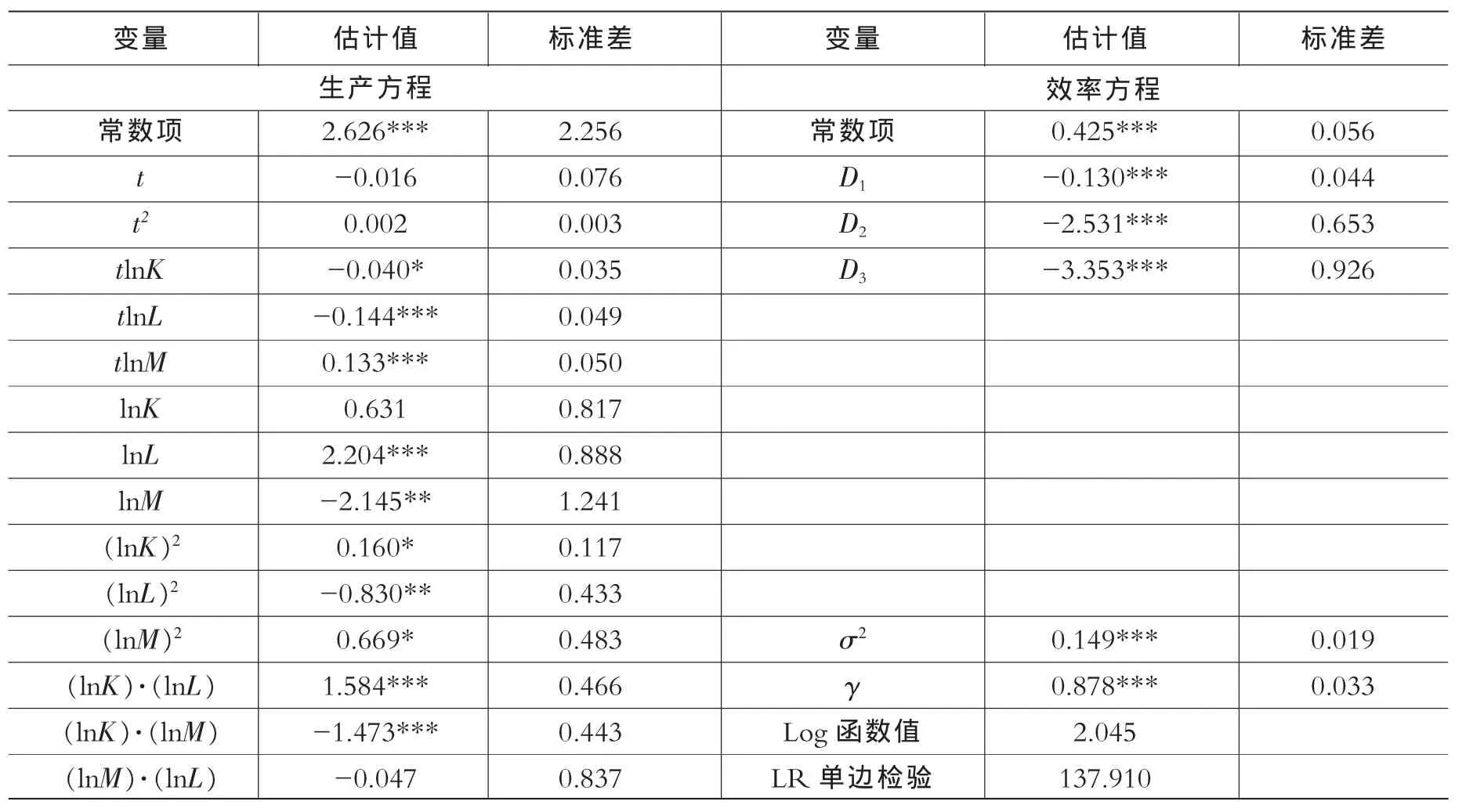
表1 随机前沿超越对数模型生产方程与效率方程

由表1中的t项系数分析可知，时间变量t和t2的系数为-0.016与0.002，接近于0且不显著，这反映出我国农业产出在2000—2012年间处于技术进步停滞状态，甚至技术增长速度略有放缓。同时，各参数设置的影响生产效率的指标——D1、D2、D3都比较显著，表明采用一步法进行参数估计即考虑生产效率方程是合理的。

通过计算（受篇幅所限，每年各地区对应的要素产出弹性未逐一列出）得到的资本平均产出弹性为-0.085，劳动平均产出弹性为2.569，土地平均产出弹性为-2.552。可见：

第一，土地投入对农业产值有较大的负向影响。这表明（同时也印证了）中国农业是以土地为主要投入要素的农业，而最有可能产生要素资源浪费与误置问题的也是土地这一投入要素。在土地质量未能有效提高的情况下，盲目地扩大种植规模并未带来增产，增加农业基础设施投入、提高农业科技水平才是使我国农业增产的根本途径。

第二，资本投入对农业产值有较弱的负面影响。这说明农业生产中资本投入已开始出现过剩现象，政府对农民的直接补贴和扶持将不再发挥更多效用，应该更多地转向对新技术、新工艺、新材料的投入。

第三，增加劳动力投入有利于农业生产效率的提高。目前中国已经由农业大国成功转变为工业大国，工业化进程导致大量的农业劳动力转移至非农产业，农业生产中的劳动力趋向于不饱和状态。

（三）模型设定检验

假设2：H0，说明超越对数生产函数的设定比C-D生产函数更加合理，印证了本文理论部分的严谨和可靠性。

另外，在生产函数估计中，资本、劳动、土地及所有二次项均比较显著，再次说明采用超越对数生产函数的合理性。

（四）模型稳健性检验

1.平稳性检验

如果变量是非平稳面板序列，易发生“伪回归”现象，因此先采用LLC检验（Levin-Lin-Chu）和Fisher-ADF检验对式（21）中所有变量的面板数据进行单位根检验 （时间趋势变量显然是平稳序列，故不进行检验）。从表2的结果可以看出，各变量面板序列的LLC统计量和ADF统计量均表现为显著拒绝原假设，这意味着所有变量序列都不存在单位根，为平稳序列。。若该假设成立，则可用C-D生产函数代替超越对数生产函数进行分析。构建似然比统计量

表2 面板数据的单位根检验及结论

2.变量内生性检验

下面针对这些平稳序列进行Granger因果检验。要素投入的变化对农业产出增长产生影响，同时农业产出的变化也将诱导要素配置的调整。如果农业产出和各要素投入之间存在变量的内生性，将会使上述回归结果受到质疑。因此，本文对式（21）中各变量进行面板Granger因果检验，也就是把解释变量作为被解释变量考察原被解释变量滞后期对原解释变量的影响。限于篇幅，本文仅报告滞后三期的因变量为lnK、lnL和lnM的Granger因果检验结果（见表3）。

表3 Granger因果检验结果

可以看出，检验结果显示劳动力、土地和资本三个投入要素与农业产出间不存在明显的双向因果关系，其他变量与农业产出间也不存在因果关系，所以变量间不存在内生性。可见表1中的回归结果是可信的。

3.变量替代性检验

由表1发现资本要素投入对农业产出的影响不显著，而且从表3资本和农业产出的Granger因果检验中发现资本与农业产出可能存在一定的双向因果关系。因此，我们对资本进行变量替代，以检验回归结果的稳健性。关于资本投入量的选取，国内外文献也有用平减后的固定资产投资总额作为衡量指标的，故我们用固定资产投资总额代替资本存量进行回归检验。用固定资产投资总额代替资本存量进行回归，结果如表4所示。可以看出，表4与表1中结果的符号和显著性基本保持不变，说明分析结果具有一定的稳健性。

三、基于产出变动分解的分析

在本节，将先对相对扭曲系数进行测算和分析，初步了解中国要素扭曲的地域特点和各要素“价格税”的影响，然后通过式（23）对农业产出变动进行分解，并将农业产出各分解项对产出的贡献程度进行比较分析，了解造成农业产出变动的影响机制。

（一）相对扭曲系数的计算

根据式（20）可以得到每个地区各要素的相对扭曲系数，受篇幅所限，这里仅列出2000—2012年四大地区（东部、西部、中部和东北部地区）各要素相对扭曲系数的平均值，如表5所示。

表4 资本变量替代后的随机前沿超越对数模型生产方程与效率方程

表5 要素相对扭曲系数

总体看来，不同地区中国农业的要素价格扭曲程度均不相同，具体如下：

第一，资本投入呈现出极强的地域差异，尤其是东部地区。中国农业存在技术投入不足和金融支持不充分的状况。技术投入不足导致资本要素价格扭曲严重，要素分配不合理，农业生产效率低下；金融支持不充分使得资本“价格税”过高，农民贷款困难。这些问题都在一定程度上抑制中国农业的发展。

第二，劳动要素相对扭曲系数均接近于0，符合中国劳动成本较低、农业劳动力投入尚未饱和的现状。这种情况表明劳动力投入增加将成为提高农业生产效率的主要方式，同时也表明中国农业劳动力“价格税”主要通过产出的市场份额分布和劳动力溢出效应（K与L、L自身、L与M、L与技术进步之间相互作用对产出增加的溢出效应）影响要素配置。

第三，土地要素相对扭曲系数均大于1，表明地区i“价格税”主要通过土地市场相对扭曲系数影响要素配置，土地要素价格扭曲问题是中国农业产业化发展中不容忽视的重要问题。农业生产过程中土地价格逐步上涨和我国土地密集型农业经济增长方式相冲突，这是导致农产品生产效率低下的主要原因。

（二）产出变动的分解

这一小节将根据式（23）来考察2000—2012年主要年份区间的技术进步（TP）、技术效率的变化（TE）、市场份额变化（SS）、要素扭曲效应（DE）和要素贡献率的变化（CE）对各地区农业产出变动的贡献程度。具体分解情况如表6所示。从表6可以看出：

第一，农业产出增长主要由技术效率的变化（TE）带来，技术效率高的地区农业产出增长相应也较快。这表明历来学者针对技术效率的研究是有意义的，这是提高中国农业产出水平的主要途径。同时，各年度TE值基本维持在75%，这或许是要素扭曲限制技术效率提高对农业增产的贡献“止步不前”的表现。

第二，要素贡献率的变动（CE）对农业增产的贡献位居第二，要素产出弹性越大，要素贡献率变动对农业产出变动的影响就越大。这进一步从具体数据证明了放宽C-D生产函数假设的必要性。另外，每一时期要素产出弹性占比的不同决定了对产出变动影响的方向。因此，这一项反映了各要素贡献率的时变值。

第三，市场份额变动的贡献（SS）接近于0，这与Aoki（2012）［11］的看法一致。这意味着市场份额变动对产出的影响可以忽视。同时，计算结果对所有年度均成立，这表明中国农业已经进入了规模报酬递减阶段，生产中要素投入难以得到有效配置和协调，要素扭曲现象较严重。这进一步说明了运用C-D生产函数进行研究的不合理性。

第四，技术进步（TP）的贡献较小，且基本为负值，这表明中国农业存在严重的技术退步现象。从2006年起，虽然中性技术进步贡献率不断增长，但其增速始终未超过偏向性技术进步率降低的速度。负的偏向性技术进步率是技术进步带来产出损失的直接原因，反映了要素市场扭曲条件下我国农业技术进步呈现出偏向性，而且这种技术进步偏向性始终对产出产生负向影响［27］。这同时也印证了通过超越对数生产函数进行模型构建的必要性和合理性。

第五，要素扭曲效应的贡献（DE）加总均为负，这是产出负增长的主要来源，是中国农业未实现资源有效配置的有力证据，也体现了“价格税”主要通过相对扭曲系数影响各地区的要素配置。另外，土地要素扭曲问题最严重（DEM占比最大）。随着“房地产泡沫”的发展，越来越多的土地价格提高（这等同于土地要素“价格税”增加），造成了土地要素扭曲，用于农业用途的土地面积减少，土地投入一直未能达到饱和，直接导致农业减产。关于这一效应的具体分析见下一小节。

（三）要素价格扭曲效应的再分解

上一小节对产出变动的分解说明，要素扭曲效应（DE）是“价格税”对要素配置的作用，反映了这种作用对农业产量变动的影响。本节将对这一效应进行再分解，研究各要素“价格税”对农业产出变动的传导机制是如何具体展开的。

根据式（26）、式（27）和式（28），可以得到各年30个省、自治区、直辖市要素市场扭曲带来的产出变动情况。为了节约版面，这里仅列出四大地区各要素价格扭曲带来的平均产出变动情况，具体见表7。

表6 产出变动分解

表7 四大地区DE分解

从表7可以看出：

第一，总体来说，要素扭曲效应DE的贡献基本为负，印证了要素误置会带来农业产出损失的事实。

第二，从四大地区的要素扭曲效应DE的贡献情况看，总体要素扭曲程度最高的是中部地区。现阶段，经济发展较落后的中部地区是主要的农业生产地域，由于技术落后，机械化水平较低，中部地区的农业主要靠资本、劳动、土地投入实现增产，这必将带来要素成本的增加，进而抑制经济增长。

第三，对比三种投入要素的要素价格扭曲效应，与表5显示的一样，土地要素存在最严重的扭曲现象。因此，要促进农业发展，提高农业生产效率，实现各地区要素的合理有效配置，应首先从土地要素入手，改变土地资源的供求关系，为农民创造更好的生产环境。

第四，观察直接效应和溢出效应下的要素扭曲贡献，发现直接效应下的要素价格扭曲对农业增产的贡献基本大于外溢效应下要素价格扭曲对农业增产的贡献程度。这表明虽然直接效应下的要素扭曲贡献是要素价格扭曲效应的主要来源，但是不同要素价格扭曲相互作用带来的产出损失大于单个要素自身价格扭曲带来的产出损失。以资本要素为例，如果资本价格上涨而其他要素价格处于无扭曲状态，那么其他要素价格相对于资本价格是下跌的，在这种情况下，增加其他要素的投入量即可带来增产；如果资本价格上涨的同时其他要素价格也在上涨，那么整个要素市场成本过高，农户将面临无法有效进行要素搭配以获得最大利润的状况。很显然，各投入要素价格扭曲现象是相关联的。关于要素价格扭曲效应的分解验证了用超越对数生产函数替代C-D生产函数进行要素误置的分析是合理的，也进一步说明要根本解决农业生产中的要素价格扭曲问题，需对投入要素之间的配置进行整体治理，把握要素间价格扭曲的相互作用。

四、结论和政策建议

本文在Aoki（2012）［11］的理论框架基础上纳入了农业最主要的投入要素——土地，同时建立了更具有说服力和灵活性的超越对数生产函数的随机前沿模型进行系数估计，通过对产出变动的再分解，从理论和实证两个方面验证和分析了要素误置抑制农业产出的作用机制，弥补了C-D生产函数无法考虑要素间扭曲相互作用的不足，分析了“价格税”对农业产出损失的影响机制。

首先，通过对要素扭曲程度的测度，发现劳动、资本、土地三大要素的扭曲程度各不相同。其中，土地要素的扭曲程度最严重，而资本要素的扭曲存在极强的地区差异。其次，在测度要素扭曲程度的基础上对产出变动进行分解，发现中国农业已经进入规模报酬递减阶段，生产中要素投入难以得到有效配置和协调，要素扭曲现象较严重。其中，产出负增长的主要来源“要素扭曲效应”是中国农业未实现资源有效配置的有力证据，也体现了“价格税”造成产出损失的传导机制主要通过相对扭曲系数影响各地区的要素配置，形成要素扭曲效应（DE），进而导致产出损失。最后，再分解产出变动中的“要素扭曲效应”（DE），观察直接效应和溢出效应下的要素扭曲贡献，发现直接效应下的要素价格扭曲对农业增产的贡献大于外溢效应下要素价格扭曲对农业增产的贡献程度，要素间价格扭曲相互作用对农业产出的影响不可忽视。

本文强调了改善要素间价格扭曲相互作用对于稳定中国农业生产的重要实践意义，这也是中国农业发展的又一大挑战。由于要素误置比较严重，仅仅通过引进先进技术和加强基础设施建设来改善农业产出并不能完全消除农业生产效率低下的状况。本文传导机制的研究表明，只有从改革价格机制出发，在考虑要素自身价格扭曲的同时关注要素间价格扭曲的相互作用，从自身扭曲水平和扭曲发散程度两个方面同时改善要素配置情况，才能真正实现长期的要素有效配置帕累托状态。

总体看来，要提升中国农业的生产效率，一方面要靠技术的提升，另一方面则是靠要素的有效配置。虽然靠技术提升带来的农业生产效率的提高程度是巨大的（表现为“自增长效应”贡献最大），但要素价格扭曲逐渐积累带来的产出损失不容忽视。因此，只有在引入技术的同时优化各要素间的配置，实现各地区间要素的合理分配，从整体治理入手，达到资源利用效率的帕累托最优状态，才能保证中国农业的长期、稳定发展。

［1］JOHNSON D G.Agriculture and the wealth of nations［J］. American economic review,1997,87（2）:1-12.

［2］WIENS T B.Technological change［M］//BARKER R. The Chinese agricultural economy.Boulder CO:Westview press,1982：67-86.

［3］MCMILLAN J,WHALLEY J,ZHU L J.The impact of China’seconomic reformson agriculturalproductivity growth［J］.The journal of political economy,1989,97（4）: 781-807.

［4］FAN S G.Effects of technological change and institutional reform on production growth in Chinese agriculture［J］. American journal of agricultural economics,1991,73（2）: 266-275.

［5］LIN J Y.Rural reforms and agricultural growth in China［J］.The american economic review,1992,82（1）:34-51.

［6］杨刚,杨孟禹.中国农业全要素生产率的空间关联效应——基于静态与动态空间面板模型的实证研究［J］.经济地理,2013（11）:122-129.

［7］彭代彦,吴翔.中国农业技术效率与全要素生产率研究——基于农村劳动力结构变化的视角［J］.经济学家, 2013（9）:68-76.

［8］潘丹,应瑞瑶.资源环境约束下的中国农业全要素生产率增长研究［J］.资源科学,2013（7）:1329-1338.

［9］应瑞瑶,潘丹.中国农业全要素生产率测算结果的差异性研究——基于Meta回归分析方法 ［J］.农业技术经济, 2012（3）:47-54.

［10］HSIEH C,KLENOW P.Misallocation and manufacturing TFP in Chinaand India［J］.Quarterly journalof economics,2009,124（4）:1403-1448.

［11］AOKI S.A simple accounting framework for the effect of resource misallocation on aggregate productivity［J］.Journal of the Japanese and international economics,2012,26（4）: 473-494.

［12］陈永伟,胡伟民.价格扭曲、要素错配和效率损失：理论和应用［J］.经济学（季刊）,2011（7）:1401-1422.

［13］曹东坡,王树华.要素错配与中国服务业产出损失［J］.财经论丛,2014（10）:10-16.

［14］朱喜,史清华,盖庆恩.要素配置扭曲与农业全要素生产率［J］.经济研究,2011（5）:86-98.

［15］JULIANOJ,ASSUNCAO,MAITREESHG.Canunobserved hete rogeneity in farmerability explain the inverse relationship between farm sizeand productivity［J］. Economics letters,2003,80（2）:189-194.

［16］李谷成,冯中朝,范丽霞.小农户真的更加具有效率吗？——来自湖北省的经验证据［J］.经济学（季刊）,2010（1）: 95-124.

［17］TASSO A,DIEGO R.The size distribution of farms and international productivity differences［R］.Working papers tecipa-480,University ofToronto,Departmentof economics.2013.

［18］BATTESE G E,COELLI T J.Frontier production functions, technical efficiency and panel data:with application to paddy farmers in India［J］.Journal of productivity analysis, 1992,（3）：153-169.

［19］孙昊.小麦生产技术效率的随机前沿分析——基于超越对数生产函数［J］.中国人口·资源与环境,2014（1）:42-49.

［20］李谷成.技术效率、技术进步与中国农业生产率增长［J］.经济评论,2009（1）:60-68.

［21］郭军华,倪明,李帮义.基于三阶段DEA模型的农业生产效率研究［J］.数量经济技术经济研究,2010（12）:27-38.

［22］YOUNG A.Gold into base metals:productivity growth in the People’s Republic of China during the reform period［R］.NBRE working paper,2000,（7856）:38-52.

［23］李宾.我国资本存量估计的比较分析［J］.数量经济技术经济研究,2011（12）:21-36.

［24］蔡晓陈.中国资本投入：1978—2007——基于年龄-效率剖面的测量［J］.管理世界,2009（11）:11-20.

［25］王志平.生产效率的区域特征与生产率增长的分解——基于主成分分析与随机前沿超越对数生产函数的方法［J］.数量经济技术经济研究,2010（1）:33-43.

［26］BATTESE E,COELLI T.A model of technical inefficiency effects in stochastic frontier production for panel data［J］. Empirical economics,1995,（20）:325-336.

［27］董直庆,陈锐.技术进步偏向性变动对全要素生产率增长的影响［J］.管理学报,2014（8）:1199-1207.

【责任编辑 王建增张跃胜】

The Loss Caused by Factor Misallocation to the Agricultural in China: Based on a Stochastic Frontier Trans-log Production Function Model

CHENG Liwen,XU Ye,TAO Changqi
（School of Statistics,Jiangxi University of Finance and Economics,Nanchang,Jiangxi,330013）

This paper incorporated land,the most important input factor of agriculture,based on the theoretical framework of Aoki (2012),and,meanwhile,set a stochastic frontier trans-log production function model to estimate the parameter.It both theoretically and empirically verifies the inhibition of the factor misallocation on the agricultural production via a re-decomposition of the output changes and makes up the shortfall of C-D production function,which does not consider the interaction of the factor distortions.It shows that:First of all,there exists the factor misallocation in agriculture.The land distortion is the most serious one compared with other factors;and the misallocation in central region was the most serious one compared with those in other regions.What's more,the misallocation of agricultural factors leads to the output loss.With the re-decomposition of the distorting effects,we find that the output loss resulting from the interaction of the price distortions of the factors is greater than the output loss resulting from the price distortions itself.The empirical study shows that the analysis based on the trans-log production function is more reasonable than the one based on the C-D production function.

Agricultural Input,Misallocation of Resources,Agricultural Economy,Price Distortion,Trans-log Production Function

F323

A

1674-6511（2016）01-0024-11

2015-11-05

国家自然科学基金(71273122、71473109、41461025)；教育部人文社会科学研究一般项目(15YJA630079)；江西省社会科学“十二五”（2015年）规划项目(15YJ26)。

程丽雯（1989-），女，江西于都人，江西财经大学统计学院博士研究生。研究方向：数量经济学。徐晔（1962-），女，江西南昌人，江西财经大学统计学院教授，博士生导师。研究方向：数量经济学。陶长琪（1967-），男，江西临川人，江西财经大学统计学院教授，博士生导师。研究方向：数量经济学。