关于加权Voronoi图离散构造法的正确性研究

李璟莹, 王斌君

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

关于加权Voronoi图离散构造法的正确性研究

李璟莹, 王斌君

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

针对加权Voronoi图离散构造法的正确性问题，系统研究了Voronoi图的原始定义和性质，并对照加权Voronoi图的逐点扫描算法，发现离散构造法是一个粗略的算法，在生成具有多个离散区域的加权Voronoi图时，该算法不正确；通过实验也证实了离散构造法的错误。通过分析离散构造法的算法，发现其扩展终止条件有错误，提出了相应的改进算法，保证了算法结果的正确性。

加权Voronoi图； 分区加权Voronoi图； 离散构造法； 逐点扫描法

0 引言

Voronoi图解决了平面上离散生成元的空间划分问题，是描述空间邻近关系的一种基础数据结构，适用于解决几何重构、覆盖模拟、路径规划、空间分析等问题，在气象学、地理学、晶体学、信息科学、机器人路径规划等领域应用广泛[1]。

最初的Voronoi图是基于最短距离的空间剖分[2]，考虑的因素比较理想化，但在实际应用中生成元往往具有不同的“影响力”，于是又扩展出加权Voronoi图[2]、分区加权Voronoi图[3]、线段加权Voronoi图[4]等各种加权Voronoi图。

对于生成元被加权的Voronoi图，生成算法包括矢量算法和栅格算法。矢量算法结果精确但计算复杂，栅格算法相对简单但精度受栅格大小影响。在栅格算法中，常用的有离散构造法和逐点扫描法。1980年， B.N.Boots提出的模拟生长模型(Growth Simulation Model)奠定了离散构造法的基本思路，即通过模拟母点的动态生长过程来生成Voronoi图[2]。1996年，Watanabe T等人按照模拟生长的思想，提出了用于生成Voronoi图的离散构造法[5]。随后，离散构造法被不断完善，适用于加权Voronoi图[6]、分区加权Voronoi图[3]、线段加权Voronoi图[4]等。离散构造法不涉及复杂运算，实现简单，适用于各类生长元。

逐点扫描法是计算每个栅格与所有生成元的距离(欧氏距离、棋盘距离、街区距离等)来确定最近生成元。1998年张有会提出了逐点扫描法生成Voronoi图[7]，该方法是按照定义来计算距离，结果准确。

1 基本概念及性质

1.1 相关概念

下面分别给出Voronoi图、加权Voronoi图和分区加权Voronoi图的定义。

定义1 Voronoi图

设S={p1,p2,…,pn}是二维欧氏空间上的一个点(也称生成元)集合，称

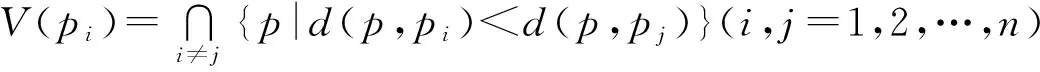
定义2 加权Voronoi图

设S={p1,p2,…,pn}为二维欧氏空间上的一个点集合，对每个点pi赋予正实数权重

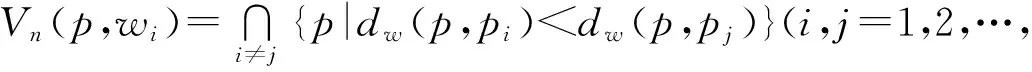
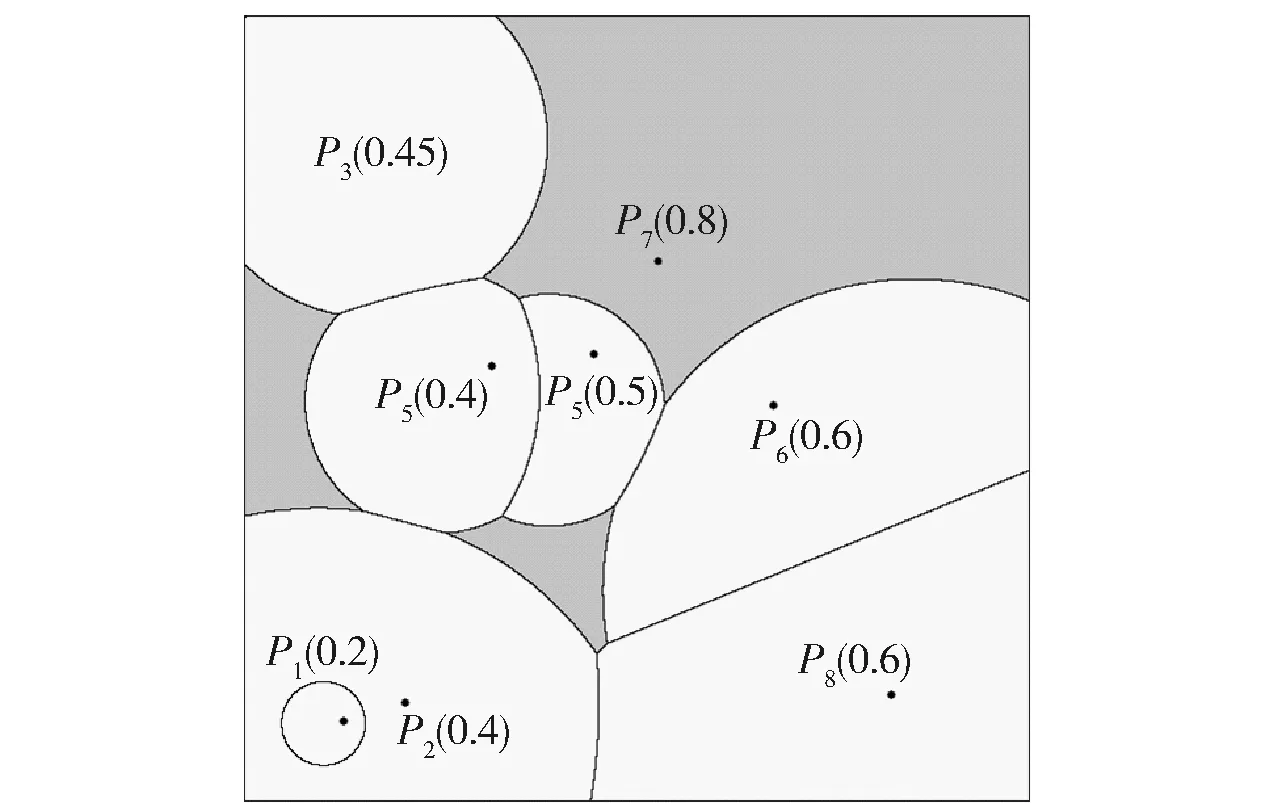
图1 加权Voronoi图

定义3 分区加权Voronoi图

设S={p1,p2,…,pn}为二维欧氏空间上的一个点集合，对每个生成元pi，以pi为原点、水平向右为坐标轴的正向，建立极坐标系，将生成元pi周围区域分成mi个扇区，以θ=αik(k=1,2,…,mi)为扇区分界线，其中，0<αi1<αi2<…<αimi<2π，并给每个扇区赋予权重wik(k=1,2,…,mi)，称

为点pi在第k扇区的权重为wik的Voronoi区域，或称点pi的第k加权扇区[3]。

1.2 相关性质

凡是生成元被加权的Voronoi图都具有以下典型性质[2-3]：

(1)相邻两个生成元pi和pj之间的边界是一条直线(当wi=wj，i≠j)或阿波罗尼圆(当wi≠wj，i≠j)。在图1中，p6与p8的权重大小一样，两者的分界线是直线，而其他生成元之间的边界线都是圆弧。

(2)“洞”的存在。当一个生成元权重与相邻生成元权重相比足够小时，该生成元的加权Voronoi区域可能完全被另一个生成元的加权Voronoi区域包围，如图1所示，p1的覆盖区域完全被p2的覆盖区域包围。

(3)越区覆盖。某个生成元的加权Voronoi区域可能由若干块不连续的区域组成，即某个生成元的加权Voronoi区域可能跨越其他生成元的加权Voronoi区域。如图1所示，p7的权重最大，它的加权Voronoi区域跨越了p4和p5的加权Voronoi区域。

由于难以直观判断一个生成元是否存在越区覆盖，所以前人虽然提出过该性质，但在设计生成算法时往往会忽略该性质。越区覆盖作为加权类的Voronoi图的一种性质，虽然有时会出现这种情况，但它反映了权重分布的不均衡，在实际应用中能帮助发现和分析问题，例如基站、变电站等设备的功率设定过大和覆盖盲区等问题。

2 离散构造法的正确性分析

在对比离散构造法和逐点扫描法的性能时，两种算法在大多数情况下结果一致，但在生成加权类的Voronoi图时，部分结果存在明显差异。下面从实验证实和理论分析两个方面分别进行阐述。

2.1 实验证实

实验1：加权Voronoi图实验。

图2和图3是分别使用两种生成算法得到的关于12个生成元的加权Voronoi图。比较发现，图2中的p7仅覆盖了①区域，而图3中的p7却覆盖了①、②、③三块不连续的区域，其余部分的空间划分是一致的。

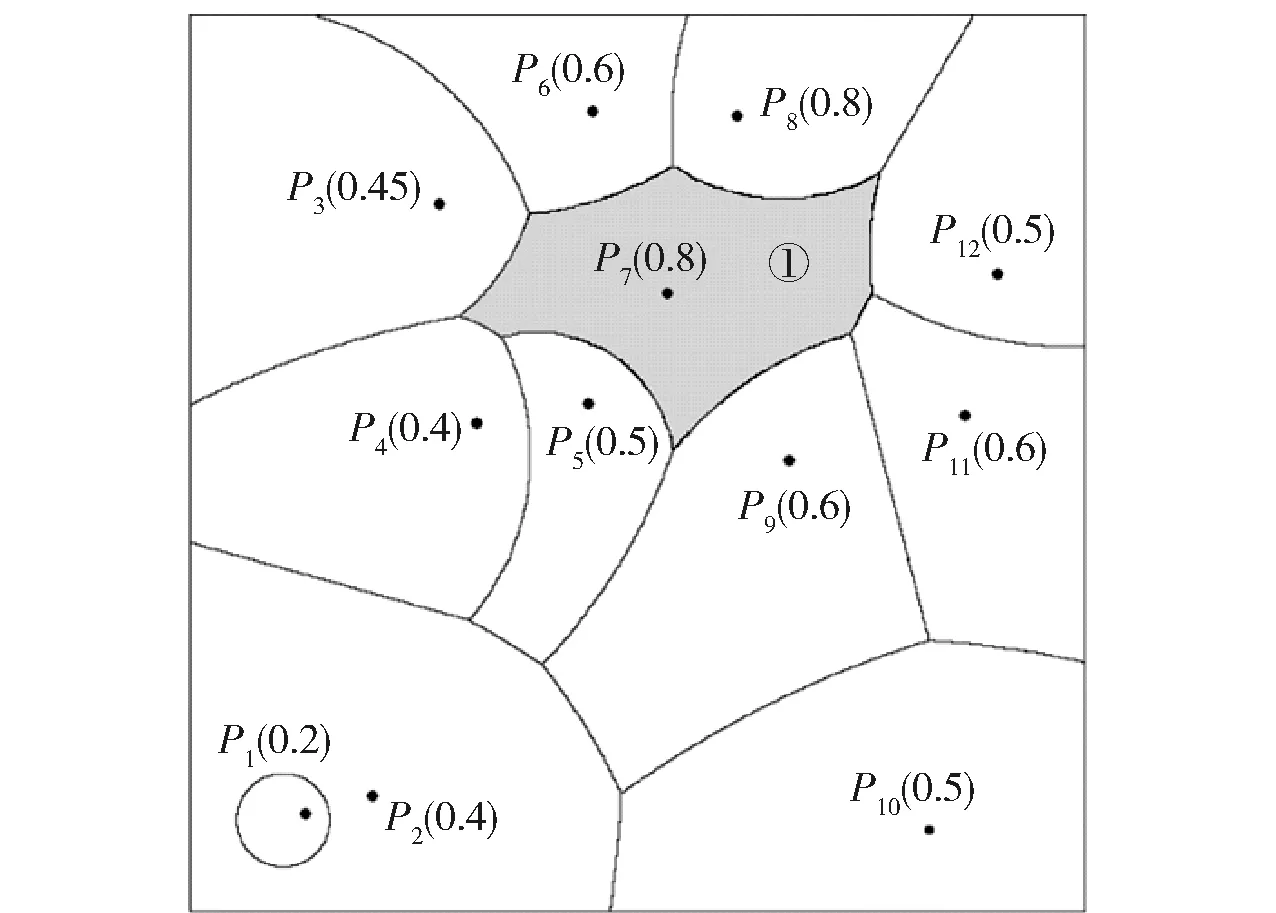
图2 加权离散构造法的结果

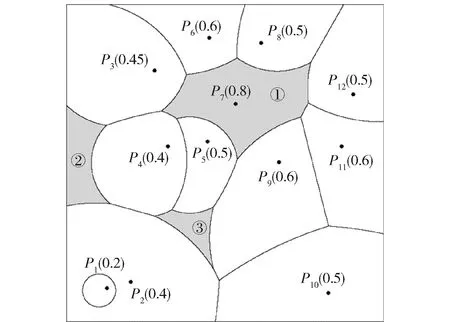
图3 加权逐点扫描法的结果

实验2：分区加权Voronoi图实验。

图4和图5分别是使用两种生成算法得到的关于10个生成元的分区加权Voronoi图。比较发现，图4中p6的第二加权扇区仅覆盖了①区域，而图5中p6的第二加权扇区却覆盖了①、②、③三块不连续区域。

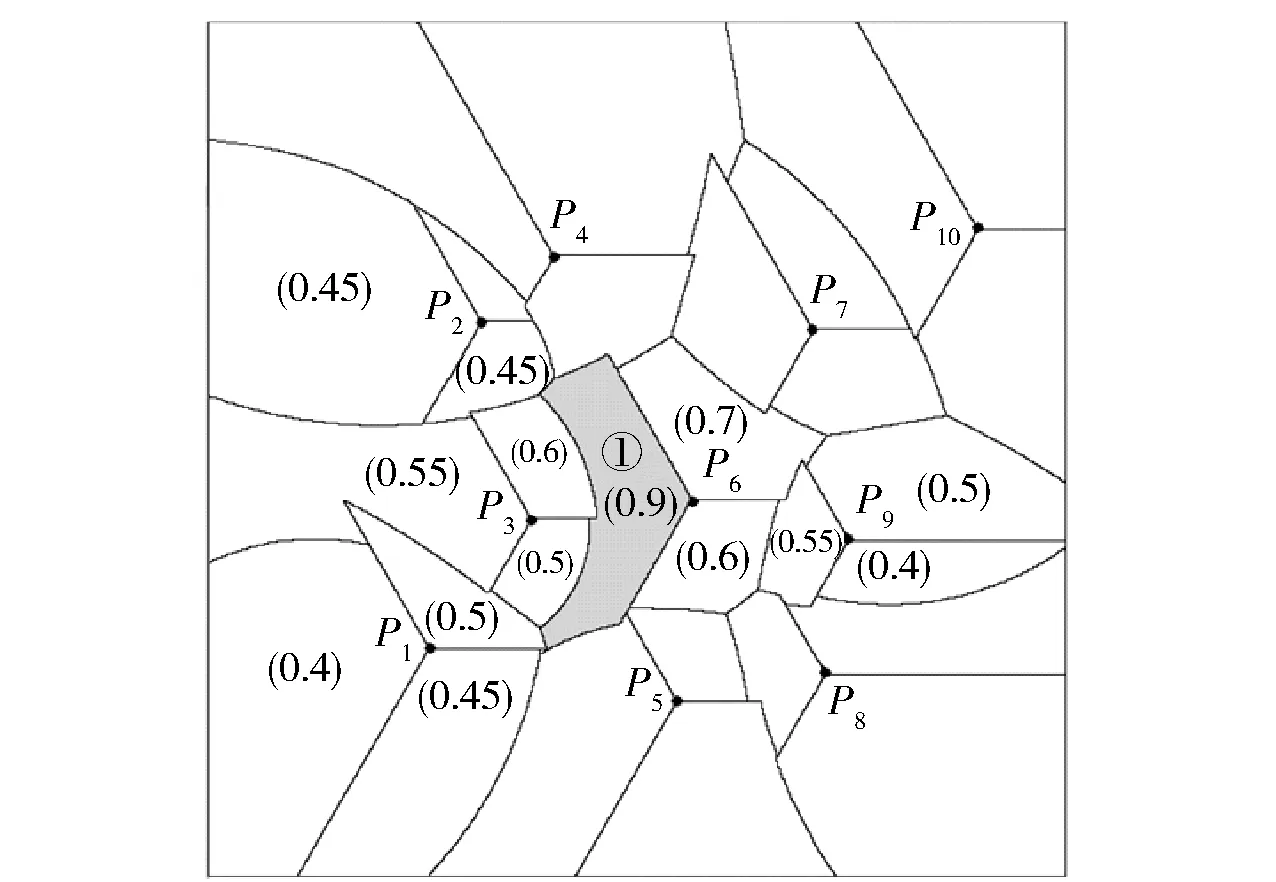
图4 分区加权离散构造法的结果

图5 分区加权逐点扫描法的结果

实验结果显示，对于同一生成元，离散构造法得到的覆盖区域是一块、连续的，而逐点扫描法得到的覆盖区域是多块、不连续的。

2.2 理论分析

按照定义，所有Voronoi图都是按照最邻近原则进行空间划分，加权类Voronoi图的衡量标准是加权的欧氏距离。逐点扫描法通过计算加权距离得到每个像素点的最近生长元，思路与定义一致，所以结果是准确的。

那么，离散构造法为什么会出现与逐点扫描法不同的结果呢？

从WatanabeT提出离散构造法到后来人们不断扩展其应用，离散构造法都遵循与算法1同样的算法思路[3-6]。

算法1：原离散构造法。

(1)初始化，建立集合S，用于存放所有待扩张的生成元。

(2)S中的生成元(扇形)依次一层层向外扩张画圆(弧)，每次画圆(弧)的半径与权重成正比，所有生成元(扇区)填涂的颜色互不相同，扩张过程中只填涂空白栅格。

(3)扩张终止条件：在画某一层圆周时，如果该层圆周上的栅格都已被填涂，则判断该生成元的Voronoi区域(加权Voronoi区域)生成完毕，就将该生成元从S集合中删去。直到S集合中没有生成元，画图结束。

(4)扫描全屏幕，提取边界。

按照离散构造法的终止条件，当算法扩张到某个时刻，如果某个生成元的扩张空间被其他生成元完全包围，该生成元就会从S中删除，即不再扩展，如图6中的P7。这意味着在该判定条件下任何生成元都不可能生成多块、不连续的覆盖区域。

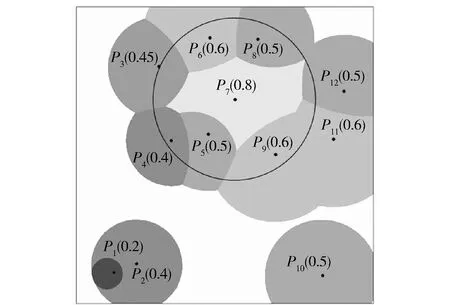
图6 加权Voronoi图的离散构造法过程

3 改进的算法

通过以上分析，在遵循B.N.Boots模拟生长模型的基础上，为了确保所有生成元能正确地按照权重正比例扩张，需要将WatanabeT提出的离散构造法终止条件设为“某层扩张圆周的全部栅格都超出屏幕边界”。

下面以加权Voronoi图的生成为例，给出改进的算法，如算法2所示。

算法2：改进的离散构造法。

输入：生成元集合S={p1,p2,…,pn}，生成元权重的集合W={w1,w2,…,wn}。

输出：以S为生成元集、W为权重的加权Voronoi图。

Step1：建立集合L，用于存放待扩张的生成元数据，L=S，扩展半径r=1。

Step2：给每个生成元赋予各不相同的颜色，使得相邻加权Voronoi区域可以区分开。

Step3：当L不为空时，执行如下循环：

{

对L中的每个元素pi，执行如下循环：

{

f=0；∥用于判断某层扩张圆周的栅格是否都超出边界；

对生成元pi在扩展半径为r*wi的圆周上的每个点，执行以下循环：

{

如果没有超出整个区域的边界，则f=f+1，并将空白栅格填涂为所设的颜色；

}

圆周扫描结束后，如果f=0，则表明该圆周上的所有栅格都超出边界，将该生成元从L中删除。

}

r++；

}

Step4：依次横向和纵向扫描屏幕，将与后继栅格颜色不同的栅格设置为黑色。

Step5：横向扫描全屏幕，将非黑色栅格置为白色，提取加权Voronoi图的边界。

经实验比对，改进算法与逐点扫描法的生成结果一致，保证了正确性，但是改进算法相比原离散构造法需要扫描更多次数，时间复杂度更高。

4 结束语

模拟生长模型提出了一种Voronoi图的生成方法，后人提出的离散构造法是该模型的一种具体实现。本文通过对比试验和理论分析，找出了离散构造法存在的问题，并提出了一种改进算法，在继承原有算法思想的基础上，保证了算法的正确性。但不足之处是，改进算法的效率较低，未来还需要仔细研究越区覆盖的特征和规律，就如何降低时间复杂度开展进一步研究。

[1] MU L. Polygon Characterization With the Multiplicatively Weighted Voronoi Diagram?[J]. The Professional Geographer，2004，56(2)：223-239.

[2] BOOTS B N. Weighting thiessen polygons[J]. Economic Geography，1980，56(3)：248-259.

[3] 马立玲. 分区加权Voronoi图的生成及其面积计算[D]. 石家庄：河北师范大学, 2004.

[4] 董蕊, 张有会, 刘淑娟,等. 线段加权Voronoi图的离散生成算法的研究与实现[J]. 计算机应用与软件, 2009, 26(7):245-247.

[5] WATANABE T，MURASHIMA S. A method to construct a Voronoi diagram on 2-D digitized space in O (1) computing time[J]. IEICE Trans. DI，1996，79：114-122.

[6] 赵志辉, 李平, 黄晓芹. 加权Voronoi图的离散生成[J]. 计算机应用与软件, 2007, 24(1):135-136.

[7] 张有会.关于加权Voronoi图的研究[D].北京：北京航空航天大学,1998.

(责任编辑 于瑞华)

李璟莹(1992—)，女，湖南怀化人，2014级在读硕士研究生。研究方向为网络安全执法技术、公安信息化。

O18