基于局域交互和全局广播的创新传播模型研究

于明亮，韩景倜，林坚洪，刘建国(.上海财经大学信息管理与工程学院，上海 200433；2.上海理工大学 a.经济管理实验中心，b.复杂系统科学研究中心，上海 200093)

基于局域交互和全局广播的创新传播模型研究

于明亮1,2a，韩景倜1，林坚洪2b，刘建国2b
(1.上海财经大学信息管理与工程学院，上海 200433；2.上海理工大学 a.经济管理实验中心，b.复杂系统科学研究中心，上海 200093)

考虑公共媒体对创新传播的影响，本文提出基于网络局域交互和全局广播的创新传播模型，该模型既考虑了创新传播过程中邻居节点之间的交互作用，也考虑了公共媒体对创新传播的影响。实证网络数据集上的仿真结果表明在公共媒体宣传力度有限的情况下，局域交互特性对创新传播具有重要影响。进一步的分析表明，结合网络结构和创新传播机制的节点影响力评价指标可以准确地对创新传播中的节点影响力进行排序，相对于度、紧密度等方法，该方法的Kendall's Tau可以提高39.19%，35.61%和33.03%。

创新传播；局域交互；全局广播；节点影响力

0 引言

创新传播主要指某种创新(思想) 通过一些特定的渠道，在社会系统中传播的过程[1]。网络科学的兴起为定量地分析创新传播模型与网络结构的关系提供了契机[2]。黄伟强等[3]基于ER随机图模型建立创新扩散网络，研究了创新潜在采纳主体行为、网络结构和性质对创新扩散的影响。段文琦等[4]基于复杂网络理论框架研究了扩散系统中采用网络和扩散初始条件对扩散模式的影响。张晓军等[5]基于随机阈值模型, 研究了社会关系网络密度对创新扩散的影响。周琪萍等[6]基于Agent的建模思想和方法, 研究了创新扩散在无标度网络和小世界网络的差异性。Pegoretti[7]研究了网络结构和信息机制设计对创新扩散的影响。罗晓光等[8]研究了网络密度和初始创新者数目与扩散绩效的关系。随着在线社交媒体越来越引起人们的关注，除了公共媒体之外，局域交互作用在创新传播过程中扮演着越来越重要的角色[9-12]。本文考虑公共媒体对创新传播的影响, 提出基于局域交互和全局广播的创新传播模型, 与经典的(Susceptible-Infected,SI)模型[13]相比，该模型既考虑传播过程中邻居节点间的交互作用, 也考虑到公共媒体宣传力度的影响。当不存在公共媒体影响时，本文的创新传播模型将退化为SI模型。通过对创新传播中的节点传播能力分析发现，在公共媒体宣传力度有限的情况下，网络初始节点选择的差异性对创新传播有着显著的影响。随着互联网的快速发展，社交网络逐渐在广告、营销中扮演着重要的角色[14]。如何找出有影响力的节点作为传播源，对创新传播具有重要的意义。创新传播中节点影响力不仅取决于网络的拓扑结构也受到创新传播机制的影响[15-17]。本文结合网络拓扑结构和创新传播过程，计算了各节点创新传播范围的期望值，进而对节点影响力进行排序，实证网络数据集上的仿真结果仿真表明：本文提出的方法可以准确地刻画创新传播网络中节点的影响力，且相对于度[18]、紧密度[19]K-核分解方法[20]，该方法可以更加准确地对创新传播中的节点影响力进行排序。本文的研究对网络中初始传播节点的选择具有非常重要的借鉴意义。

1 创新传播模型的构造

评价节点i在创新传播中的影响力时，其创新传播过程主要包过两个阶段，即创新传播初始阶段和创新传播阶段。具体如下：

1)在创新传播初始阶段，即t=0时，假设网络中节点i为初始采纳者，状态记为1，其它节点为未采纳者，状态记为0；

经过一定的时间步长T，网络中采纳者的数量为节点i的创新传播范围，定义为该节点的影响力。当时间步长T足够大时，网络中所有的节点都将变为采纳者，此时无法区分各个节点的影响力，为此只观察特定步长T下，网络中节点i的创新传播范围，本文设T=5或T=10，T的大小取决于网络的规模。评价节点在创新传播中的影响力时，独立重复此节点创新传播3×104次。

2 节点影响力评价指标

对于特定网络结构，传播源的选择对于创新传播具有重要的意义。随着社交网络的发展，如何找出有影响力的节点作为初始采纳者将有助于扩大创新传播效果。目前主要的节点影响力指标有基于网络局部属性的度指标[18]，基于网络全局属性的紧密度指标[19]和基于网络位置的K-核分解方法[20]。节点i的度定义为节点的邻居数量，表示为

(1)

其中，n为网络节点数，aij为网络邻接矩阵A的元素。度指标刻画了一个节点的直接影响力，认为节点邻居数目越多，在网络中就越重要。度指标只考虑到节点的局部拓扑结构信息，因此很多情况下并不能精确度量节点的影响力。

紧密度指标[19]考虑节点在网络的全局信息，认为节点越居于网络中心就越重要。节点i的紧密度可以表示为

(2)

其中，n为网络节点数，dij为节点i到节点j的最短距离。

Kitsak等[20]认为，网络中节点的影响力取决于节点在网络中的位置，提出了K-核分解方法，该方法层层删去网络中外围的节点，处于内层的节点具有较高的影响力。具体分解方法如下[20]: 网络中如果存在度为1的节点，将这些节点删去，删掉后的网络如果还存在度为1的节点，再将这些节点删去。重复操作，直到网络中没有度为1的节点为止。删去的这些点组成一个层，这一层所有节点的K-核值为1。对于一个节点而言，剥掉一层后，网络中剩下的节点的度称为该节点的剩余度。继续剥核，去掉网络中剩余度为2的点，直到网络中所有节点被删除为止。

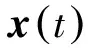
(3)

(4)

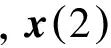
(5)

(6)

……

(7)

由数学归纳法可知式(4)成立。因此在t时刻网络中各节点变为采纳者的累积概率为

(8)

(9)

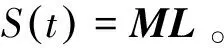
3 节点影响力评价指标

表1 网络属性

Tab.1 Network features

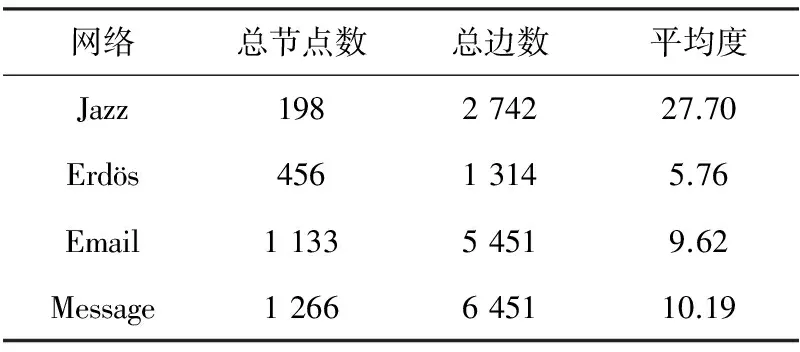
网络总节点数总边数平均度Jazz198274227．70Erdös45613145．76Email113354519．62Message1266645110．19

3.1 实验数据及网络属性

本文实验数据采用了4个实证网络，分别是：Jazz[21]、Erdös、Email[23]和Message网络，Jazz网络是一个Jazz音乐家合作网络，点代表Jazz音乐家，边表示两个音乐家之间在同一家乐队里有合作关系。Erdös网络为科研合作网络，点代表科学家，边表示两个科学家曾经合作过。Email网络的点代表西班牙罗维拉·维尔吉利大学的研究人员、学生或者管理者等，边表示成员之间有过email交流。Message网络是一个在线社交网络，每个点代表加利福尼亚大学的学生，边代表两个学生之间有过信息交流。

3.2 初始节点选择差异性对创新传播的影响

采用创新传播模型分析不同公共媒体宣传力度p下，初始节点选择对创新传播的影响。对于小规模网络Jazz网络实验步长取T=5，另外3个网络取T=10。图1给出了公共媒体宣传力度p为0.000 5，0.001 0和0.002 0时，分别以网络中度大的节点作为传播源和随机选择节点作为传播源创新传播范围的差异性。横坐标是创新传播网络内部传播率q，纵坐标是创新传播范围提高率ρ，其中，wmax为以网络中度最大的节点作为传播源时的创新传播范围，wr为以网络中随机选择节点作为传播源的创新传播范围。ρ值越大，说明网络传播源选择的差异性对创新传播影响越大。从图1可知，在相同传播率q下，随着公共媒体宣传力度q逐渐变小，创新传播范围的差异性逐渐变大。当q=0.000 5时，初始采纳者的选择对创新传播范围影响最大。从中可以得出：当公用媒体宣传力度有限时，选择有影响力的节点作为传播源，将更有助于扩大创新传播范围。

(10)

3.3 节点影响力评价指标与节点创新传播能力的相关性分析

本文采用Kendall's Tauτ[24]系数来度量各节点影响力指标和节点创新传播能力之间的相关性。Kendall's Tau τ系数是用来计算两个序列之间排序的相关性，该值介于-1和1之间，Kendall's Tau τ系数越接近于1说明两个序列一致性越高，则该指标越能准确地对创新传播网络中的节点传播能力进行评价。具体计算为

(11)

图3给出了新指标相对于其它节点影响力评价指标度量节点创新传播能力的Kendall's tau提高率η，具体定义如下

(12)

其中，τs为新指标的Kendall's tau τ。τ0分别为度、紧密度和K-核分解方法的Kendall's tauτ。τ>0表明新指标可以更加准确地识别创新传播中节点的影响力。从图中可以发现所有的η都大于0，说明新的指标相对于其它指标可以更加准确地识别创新传播网络中的节点影响力。相对于度，紧密度和K-和分解方法，当内部传播率q分别为0.050，0.050和0.015时，提高率η可以达到39.19%，35.61%和33.03%。

4 总结与展望

本文提出基于网络局域交互和全局广播的创新传播模型，该模型既考虑创新传播过程中邻居节点之间的相互作用，也考虑公共媒体宣传力度的影响。实验结果表明选择网络中有影响力的节点作为传播源将有助于扩大创新传播范围，且随着公共媒体宣传力度的减小，初始节点选择的差异性对创新传播效果的影响也更加明显。因此在公共媒体宣传力度有限的情况下，对网络中节点的影响力进行评价对创新传播具有非常重要的意义。本文结合网络结构和创新传播过程，提出新的评价指标。该指标通过计算网络中各节点创新传播范围的期望值评价各节点的影响力，实验结果表明本文提出的节点影响力评价指标的Kendall's tau τ介于0.941和0.985之间，说明结合网络拓扑结构和创新传播机制的节点影响力评价指标可以准确地度量节点的创新传播能力。且相对于度、紧密度和K-核分解方法，该方法的Kendall's tau τ可以提高39.19%，35.61%和33.03%。

[1]Rogers E M. Diffusion of innovations[M]. New York：Free Press， 1995.

[2]李翔,刘宗华, 汪秉宏.网络传播动力学[J]. 复杂系统与复杂性科学, 2010,7(2):33-37. Li Xiang, Liu Zonghua, Wang Binghong. On spreading dynamics on networks[J]. Complex Systems and Complexity Science,2010,7(2):33-37.

[3]黄玮强, 庄新田.基于随机网络的创新扩散研究[J]. 管理学报, 2007,4(5):622-628. Huang Weiqiang, Zhuang Xintian. Study of innovation diffusion by using stochastic network[J]. Chinese Journal of Management,2007,4(5):622-628.

[4]段文琦,陈忠, 惠淑敏.基于复杂网络的网络市场新产品扩散:采用网络和初始条件的作用[J]. 系统工程, 2007,25(5):15-19. Duan Wenqi,Chen Zhong, Hui Shumin. Diffusion of new products in network markets based on complex networks:the role of adoption network and initial conditions[J]. Systems Engineering,2007,25(5):15-19.

[5]张晓军, 李仕明, 何铮.社会网络关系密度对创新扩散的影响[J]. 系统工程, 2009,27(1):92-97. Zhang Xiaojun，Li Shiming, He Zheng. Impact of social network density on innovation diffusion[J].Systems Engineering,2009,27(1):92-97.

[6]周琪萍, 徐迪, 杨芳.基于Agent的创新扩散研究[J]. 软科学, 2014,28(1):6-10. Zhou Qiping, Xu Di,Yang Fang. Study of the agent-based mechanism of innovation diffusion[J]. Soft Science,2014,28(1):6-10.

[7]Pegoretti G, Rentocchini F, Marzetti G V. An agent-based model of innovation diffusion: network structure and coexistence under different information regimes[J]. Journal of Economic Interaction and Coordination, 2012,7(2):145-165.

[8]罗晓光, 孙艳凤.创新扩散网络结构与创新扩散绩效关系研究[J]. 科技进步与对策, 2015,32(1):2. Luo Xiaoguang, Sun Yanfeng. On the relationship between the structure of innovation diffusion network and the innovation diffusion performance[J]. Science Technology Progress and Policy,2015,32(1):2.

[9]Hou L,Pan X, Liu J G, et al.Memory effect of the online user preference[J]. Scientific Reports, 2014,4:6562.

[10] Guo Q,Shao F, Hu Z L, et al.Statistical properties of the personal social network in the Facebook[J]. Europhysics Letters, 2013,104(2):28004.

[11] Wu Y, Zhou C, Xiao J, et al. Evidence for a bimodal distribution in human communication[J]. Proc Natl Acad Sci， 2010,107(44):18803-18808.

[12] 刘咏梅, 彭琳, 赵振军. 基于小世界网络的微博谣言传播演进研究[J]. 复杂系统与复杂性科学, 2014,11(4):54-60. LiuYongmei, Peng lin,Zhao Zhenjun. The evolution of rumor spread on microblog based on small-world network[J]. Complex Systems and Complexity Science, 2014,11(4):54-60.

[13] Barthélemy M, Barrat A, Pastor-Satorras R, et al. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks[J].Physical Review Letters,2004,92(17):178701.

[14] 熊熙,胡勇. 基于社交网络的观点传播动力学研究[J]. 物理学报, 2012,61(15):104-110. Xiong Xi, Hu Yong.Research on the dynamics of opinion spread based on social network services [J]. Acta Phys Sin,2012,61(15):104-110.

[15] Klemm K, Serrano M á, Eguíluz V M, et al. A measure of individual role in collective dynamics[J]. Scientific reports, 2012,2(2)：292.

[16] Lin J H, Guo Q, Liu J G, et al. Locating influential nodes via dynamics-sensitive centrality[J].Scientific Reports，2016，6(3)：032812.

[17] Liu Y, Tang M, Zhou T, et al. Improving the accuracy of the k-shell method by removing redundant links-from aperspective of spreading dynamics[DB/OL].[2015-03-20].http：//www.nature.com/articles/srep13172.

[18] 刘建国, 任卓明, 郭强, 等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013,62(17):178901-178901. Liu Jianguo, Ren Zhuoming, Guo Qiang, et al. Node importance ranking of complex networks[J]. Acta Phys Sin,2013,62(17):178901-178901.

[19] Freeman L C. Centrality in social networks conceptual clarification[J]. Social networks, 1979,1(3):215-239.

[20] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010,6(11):888-893.

[21] 任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014,59:1175-1197. Ren XiaoLong, Lü LinYuan. Review of ranking nodes in complex networks[J]. Chin Sci Bull, 2014,59:1175-1197.

[22] Gleiser P M, Danon L. Community structure in jazz[J]. Advances in Complex Systems, 2003,6(4):565-573.

[23] Guimera R, Danon L, Diaz-Guilera A, et al. Self-similar community structure in a network of human interactions[J]. Physical review E, 2003,68(6):065103.

[24] Kendall M G. A new measure of rank correlation[J]. Biometrika, 1938:81-93.

(责任编辑 耿金花)

Innovation Diffusion Model Based on the Local Interaction and Global Broadcasting

YU Mingliang1,2a，HAN Jingti1，LIN Jianhong2b，LIU Jianguo2b

(1.School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai 200433,China；2. a.Labs of Economics and Management, b. Research Center of Complex Systems Science,
University of Shanghai for Science and Technology, Shanghai 200093,China)

In this paper, we present an innovation diffusion model based on the local interaction and global broadcasting, which considers both the interaction between each node and the influence of the public media during the innovation spreading process. The experimental results show that as the effect of the global broadcasting is limited, the local interaction relationships would play an important role in the innovation diffusion. Furthermore, the simulation results on for real networks show that under the limited influence of public media, the improved method which integrates the network structure and innovation diffusion process can evaluate the node influence in innovation diffusion accurately. Comparing with degree, closeness and K-shell method, the largest improved ratio could reach 39.19%, 35.61% and 33.03% respectively.

innovation diffusion; local interaction; global broadcasting; node influence

10.13306/j.1672-3813.2016.04.012

2015-09-08；

2016-05-20

国家自然科学基金(71171136，71271126，61374177)； 高校博士点基金(20120078110002)；上海市东方学者特聘教授项目和上海市曙光学者项目(14SG42)。

于明亮(1979-)，男，山东青岛人，博士研究生，主要研究方向为在线社会网络创新传播。

N941

A