基于节点动态连接度的网络社团划分算法

贾 珺，胡晓峰，贺筱媛(国防大学 .信息作战与指挥训练教研部; .研究生院，北京 100091)

基于节点动态连接度的网络社团划分算法

贾 珺a,b，胡晓峰a，贺筱媛b
(国防大学 a.信息作战与指挥训练教研部; b.研究生院，北京 100091)

首先定义了节点动态连接度这一概念，然后介绍了基于节点动态连接度的网络社团划分算法，之后再对其中相关参数的取值范围和社团划分结果之间的关系进行了分析，并以Zachary网络为例验证了分析结论。在此基础上，以dolphins、polbooks和football 3个实际网络为对象，进行了社团划分实验，证明了本算法可通过动态调整参数实现对不同网络的社团划分。最后将实验结果与其他几种常见的社团划分算法结果进行了比较，证明了算法的优势，并对算法中需要注意的一些问题进行了说明。

节点动态连接度；社团结构；社团划分

0 引言

网络中的社团结构指的是网络中的节点形成的多个团体，这些团体内部之间连接紧密，而团体之间的连接则相对松散[1-2]，具体结构如图1所示。很多现实中存在的网络，都表现出拥有较明显的社团结构。对于网络社团结构，特别是划分算法的研究，不但在网络科学研究方面有重要的理论意义，而且在社会学、计算机学、生物学等领域也都有实际的应用价值。

从划分后的结果来说，网络社团划分算法主要包括非重叠社团和重叠社团两大类[3]，其中非重叠社团划分算法是研究最早也是应用最广的一类算法。这一类算法主要包括最早的试探性算法Kernighan-Lin，它是通过设置一个增益函数，利用贪婪算法的原理逐步将网络划分成大小已知的两个社团的[4]；还包括基于网络特定矩阵的谱分析法，其中最典型的是利用图的拉普拉斯矩阵[5]或标准矩阵[6]进行计算，这一类算法的基本原理是在这类矩阵中，同一社团节点对应的特征分量都近似相等，利用这一原理可以较快速和准确地找到社团[7]。除了以上两类算法外，在非重叠社团划分算法中应用最广泛的一类是基于模块度(Q)的优化算法，其中主要包括凝聚、分裂两种。其中凝聚算法主要是利用自底向上，逐步聚合的思想，让每次的聚合都向着模块度增大最大的方向，直至所有边都合成一个社团为止，过程中最大Q值对应的即为社团结构。其中最典型的有Newman快速算法[8]和CNM算法[9]等；分裂算法与凝聚算法的思路相反，它是自顶向下进行的，通过不断移除网络中的边，向着模块度减小最大的方向，最终将网络中所有点都划分成独立社团，过程中最大Q值对应的即为社团结构。其中最典型的有Newman最早提出的GN算法[10]以及后来在其上的多种改进和延伸[2，11-12]等。近年来，又出现了几种其他类型的社团划分算法。其中一类搜索算法是从网络的某些特定节点开始，以相应的标准进行计算，将节点划分到不同的网络中，这一类算法有一个共同点就是计算复杂度相对较小，例如利用经典的节点相似性指标以及其他一些自定义指标进行计算的[13-16]；还有一类算法是将模拟退火[17]、遗传算法[18]等智能优化算法引入社团划分算法中，通过设定目标函数，最终得到最优或者较优的社团划分结果。

从计算复杂度角度来说，以上这些算法中利用局部节点信息的复杂度总体上要明显小于利用网络全局信息的。但传统的利用局部节点信息的算法一般没有考虑高阶邻居对网络社团划分结果的影响，导致一些社团结构无法划分出来；同时原有算法中的划分标准一般相对固定，对于不同类型的网络产生的划分效果也并不完全相同，算法的通用性方面受到了制约。

为了解决上述问题，本文首先提出了节点动态连接度这一概念，根据节点的动态连接度对网络进行社团结构的划分，同时针对不同网络动态调整节点连接度中的参数，以期得到最佳的网络社团结构划分结果。实验结果证明，这一网络社团划分算法复杂度较低，并且在多种不同类型的网络中都能得到较好的社团结构划分结果。

1 算法介绍

本算法的核心思想是采用定量化的方式，计算节点与已有社团之间的关系，通过这一关系的数量值与设定的阈值进行比较，来确定节点是否属于该社团，最终将所有节点划分到不同的社团中去，以实现对网络的社团结构划分。其中节点与社团之间的定量化关系即为本算法中定义的节点动态连接度，在节点动态连接度中还设置了一个可变参数，以适应不同网络在划分中可能产生的差异。

1.1 基本概念与定义

对于一个无向无权网络G(V,E)，其中V=[v1,v2,…,vN]为网络的节点集，E=[e1,e2,…,eM]为网络的链路集。假设网络中某已知社团为Cm，则可定义网络中的任意节点vi对于社团Cm的动态连接度为：

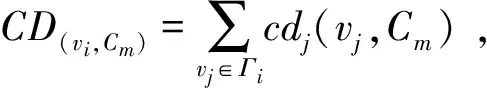
其中nvj,Cm为vj与Cm中的节点之间存在连边的个数；kvj为节点vj的度；α即为节点连接度中的可变参数。情况1)指的是若节点vi的邻居vj属于社团Cm，则这个邻居对于vi节点动态连接度的贡献值为正1；情况2)指的是若节点vi的邻居vj不属于社团Cm，但是由于其只与vi相连，因此它也不可能属于其他社团，则vj对vi节点动态连接度的贡献值同样也为1；情况3)指的是若vj不属于社团Cm，同时其度不等于1，则vj对vi节点连接度的贡献值要看它与社团Cm的连接情况，若其没有连接，则vj的贡献度为负1。而对于连接情况则主要是通过连接比率与可变参数α来确定，因此这里设可变参数的取值范围为α≥0。

通过定义1中的公式，就可以计算出任意节点与任意社团之间的连接度。在进行社团划分时，通过与设定的阈值相比较，就可以将节点划分到不同网络中。

对于网络社团的划分情况，本算法中采用模块度Q来衡量划分的质量[11]。对于模块度Q的计算，首先要假设网络被划分成k个社团，则在此基础上构建一个k×k维的对称矩阵e=(eij)，其中元素eij表示第i个社团和第j个社团之间的边在所有边中所占的比率，则模块度为

1.2 算法流程

本算法首先是通过设定一个固定的α值，然后选择起始节点并进行节点动态连接度计算和社团划分，划分完毕后计算在此α值下得到的社团划分模块度，之后再多次改变α值，最后最大的模块度所对应的即为最佳的网络社团划分结果。在固定的α值下，具体的一次社团划分算法主要是从某一个选定的节点出发，首先确定一个社团(一般选取网络中度最大的点与其邻居构成)。然后以这个社团为起点，计算所有相关邻居节点的节点连接度，若大于阈值0，则加入社团，否则不加入，重复这一过程直到没有节点能再加入这一社团为止。然后将划分好的这一社团从原有网络中剔除，再重新选取已有度最大的节点及其邻居节点构成初始社团，重复以上步骤直到所有节点都划分完毕为止。在固定的α值下，具体的一次社团划分算法可用如下几步表示：

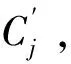
步骤3：计算每个新添加节点的所有邻居对于社团Cj的节点连接度，若大于阈值0，则将这一节点添加到社团Cj中。

步骤4：重复步骤3直到没有任何节点可以添加为止，这时的社团Cj即为网络G(V,E)中的一个社团。

步骤5：从网络G(V,E)中剔除社团Cj相关所有节点与边，形成一个新的网络G′(V′,E′)。

步骤6：以新网络G′(V′,E′)为初始网络，重复步骤1～步骤5，直到新网络G′(V′,E′)没有节点为止。这个过程中生成的所有社团集合C=[C1,C2,…,CN]即是网络G(V,E)进行社团划分后的结果。

通过以上步骤就可以得到一个固定α值下的网络社团划分结果。对于不同的α值，分别进行划分并记录下其模块度，最大的模块度所对应的既是理论上认为的最佳网络社团划分结果。

同时需要说明的是，通过定义1中的情况2)，本算法已经将可能出现的孤立节点划分到了相关社团中。因此经过Step5剔除掉相关节点和边之后，不会出现未划入社团的孤立节点。但是有可能出现孤立的节点群，而这些孤立的节点群，就是其他还未划分出来的社团结构。通过算法还可以看到，如果选取的起始节点不同或者设定的阈值不同，本算法可能会遇到的情况是在社团交界处的某些节点可能会同时属于不同社团。这一问题属于重叠社团划分中的情况，传统的重叠社团处理中，一般都是将交界处节点同时划分到不同社团中去。本算法的处理方式是将这种交界处的节点划归到先划出的社团，因此节点只会属于一个社团。

1.3 算法分析

本算法的主要特点是设置了可调节的参数α，因此α的取值范围和可能出现的结果就成为了算法设计的关键部分。根据节点连接度的定义，对于任意一个节点vi和Cm，其中vi的度为kvi，假设vi的邻居集合Γi中属于Cm的比率为x，则不属于的为1-x。又由定义可知0≤nvj,Cm/kvj≤1，设不属于Cm的节点其cdj(vj,Cm)的平均取值为β，其可能的取值范围为β≥-1。则可得到任意节点的节点连接度取值范围为

CD(vi,Cm)=kvi×x+kvi×(1-x)×β=kvi×(x+β-x·β)

(1)

由式(1)可以得到，节点连接度的正负完全由x+β-x·β确定，其中0≤x≤1。则可设：

z=x+β-x·β

(2)

由式(2)可以看出，当β≥0时，恒有z≥0。又根据节点连接度的定义，可变参数α与β之间的关系可表示为

β=m×(y+(1-y)(-1+D×α))

(3)

其中，m=kvi×(1-x)，D为nvj,Cm/kvj的平均值，y为度为1的节点在所有不属于Cm的节点中所占的比率。根据式(3)可以看出，当D×α≥1时，恒有β≥0。但是对于网络划分来说，只有当β值不是恒大于0时，才可能将网络中的节点分配到不同社团中去。因此对于本算法来说，在数学分析的基础上可以得到如下结论：即通过改变α的值，可得到不同的网络结构划分结果，而且可以看到，当α值过大时，网络会被划分成单一社团。

本文以Zachary网络[19]为实例验证以上结论。分别为α取不同的值，然后在不同的α值下依据前面介绍的算法对Zachary网络进行划分，可以分别得到如下结果：

图2中从左到右α的取值依次为0，1，2，3，每个α的对应的模块度如表1所示：

通过图2表1可以看出，对应于不同的α值，网络的划分结果是完全不相同的。而且对于过大的α值，网络最终会被划分为同一社团。这一实例证明了以上数学分析的结论。同时，这一结论也从另一个侧面说明，对于不同的网络，改变α值可以得到相对最优的划分结果，这种设置可变参数的动态划分算法是合理的。

同时在算法复杂度方面，假设网络中有n个节点和m条边，对于本论文提出的在固定的α值下具体的一次社团划分算法，其时间复杂度约为O(n2)，在稀疏网络下约等于O(mn)，可以看出这一复杂度明显优于传统的GN算法等。

2 实验

为了验证算法的有效性，本论文选取了3个实际网络数据集，这3个是在网络社团划分实验中最具有代表性的。通过改变α值，分别找到了3个网络相对最优的划分结果，并对相关实验结果进行了综合分析。

2.1 实验结果

本论文选取的数据集dolphins最早是由Lusseau博士在其2003年的文章中使用的，主要通过宽吻海豚相互间的声音研究了其社团情况[20]；数据集polbooks主要记录的是2004年美国大选期间，在Amazon上与政治相关书籍的售卖情况，其中点为书籍，边代表了两个书籍被同一人购买过，这其中的社团主要表现的是购买行为的分类；数据集football最早则是由M. Girvan 和M. Newman在其2002年文章中使用过，主要描述的是美国大学生足球在2000年秋天整个赛季的比赛情况，其中节点表示不同的队伍，而边表示的则是不同队伍之间的比赛，其中的社团代表的是不同的联盟[10]。以上这些数据集的基本参数如表2所示。

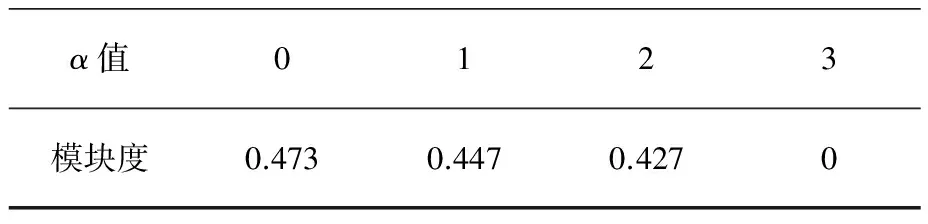
表1 不同α值下Zachary网络社团划分模块度Tab.1 different modularity of Zachary in different α

表2 网络数据集基本参数Tab.2 the basic parameters’ value of the three networks

在本次实验中α的取值从0开始，每次增加0.5，记录下每次划分结果的模块度值，直到网络被划分为一个社团、模块度降为0为止。通过多次实验，这3个数据集的社团数量划分数量和模块度值的结果如图3～5所示。

由图3可以看到，本算法对应的社团划分数量随着α值的增大，是呈阶梯状单调递减的，这是由算法本身的性质决定的。而相对应的模块度结果如图4所示：

由图4可以看到，模块度的变化却并非是单调递减的。这个结果也可由模块度计算公式推导而出，即并非社团数量越多，模块度越高。综合以上的实验结果数据可以得到：数据集dolphins最大模块度为0.584，对应的α值为{0.5,1.0}，社团数量为4；数据集polbooks最大模块度为0.563，对应的α值为{0}，社团数量为5；数据集football最大模块度为0.644，对应的α值为{2.5,3.0}，社团数量为11；具体的社团划分结果如图5所示。

从理论上来说，可以认为图5中表示的是3个网络的最优社团划分结果。

2.2 结果分析

在利用本算法进行实际的网络社团划分时，一般是通过改变算法中可变参数α的值，来获得尽量贴近于预期的社团划分结果和相对更高的模块度值，以这种方式实现算法对不同网络的最优划分。因此α值的确定方式就成为了提高算法有效性和效率的关键因素之一。由之前实验结果的图3中可以看到，随着α值的增大，网络社团的划分数量是单调递减的，但同时从图4中又可以看出，社团结果的模块度却不是单调递减，例如dolphins的最大模块度对应的α值为{0.5,1.0}，football的最大模块度对应的α值为{2.5,3.0}。而且随着网络节点规模的增大，网络最大模块度对应的α值可能会越来越大。因此本算法在实际网络的应用中，对于α值的确定，可以利用折半查找等策略，快速搜索到可能的最大模块度对应的α值，以提高算法的整体效率。同时如果在进行社团划分前已知网络的社团数量，就可以利用社团数量和α值快速找到相对应的最大模块度，这时对应的就是理论上最佳的社团划分结果。

GN算法Newman快速算法LPA算法文献[16]算法本文算法dolphins0．5190．4890．5110．550．584polbooks0．5160．5020．515-0．535football0．5990．5770．5970．5690．636

在算法的有效性方面，以算法划分网络后所求得的最大模块度值来说，本算法与其他经典算法的结果比较如表3所示。

由表3可以看到，本算法对于不同网络所能求得的最大模块度明显优于传统的经典算法。这是由于通过α值的变化，可以使算法更加适应目标网络，从而求得更好的社团划分结果。同时从前面的分析也可以看出，本算法的时间复杂度约为O(n2)，这在所有的社团划分算法中也属于较低层次，因此本算法从效率上来说也适用于大规模网络。

但同时也应该看到，本算法在计算过程中还需要特别注意的是算法中阈值的设定会影响到最终划分结果。以前面算法分析中用到的Zachary网络为例：当α=1时，与已知的实际社团结果相比，若算法中的阈值设定为0，则可得到的最优社团划分结果将节点3错误划分到了另一个社团；但是如果将算法中的阈值设定为大于0并小于1的任意值，本算法就可以找到与实际情况完全一致的社团划分结果(即可将节点3划分到正确的社团中去)，如图6所示。

因此对于不同的网络，可以在现有算法的基础上给阈值增加一个微小的扰动，以期获得最优的划分结果。同时还应该看到，本算法在利用经典的模块度进行社团划分结果的选择时，是存在一定局限性的。即最大的模块度对应的社团划分结果与实际已知的社团结构之间存在差异。例如dolphins实际应为两个社团，但是当社团数量为2时，对应的模块度并非最大，这是由于模块度本身的局限以及数据可能存在的缺陷导致的。在运用算法进行社团划分时，必须要注意这一问题。

3 结论

本算法在传统局部信息算法基础上，考虑了二阶邻居对于社团划分结果的影响，提高了算法的精度；通过设置动态可调整的参数，改变了传统算法难以适应不同网络的问题，提高了算法的动态可适应性；同时这一算法与很多传统算法相比，计算复杂度也属于较低范围，因此可应用于大规模网络的社团划分计算中。

下一步可以通过大量实验，研究参数α与模块度之间可能存在的逻辑关系，为更好地设定参数提供依据；或者可以研究在算法中引入回馈机制，将计算结果与算法中设置的动态参数以及阈值之间建立对应关系，利用机器学习等智能算法在进行社团划分时自动快速收敛到最佳结果区间，进一步提高算法的计算效率和结果。

[1]Wasserman S, Faust K. Social Network Analysis: Methods and Applications [M]. Cambridge：Cambridge University Press, 1994.

[2]Radicchi F, Castellano C, Cecconi F, et al, Defining and identifying communities in networks [J]. Proc Natl Acad Sci,2004,101(9):2658-2663.

[3]骆志刚,丁凡,蒋晓舟,等.复杂网络社团发现算法研究新进展[J].国防科技大学学报, 2011,33(1):47-52. Luo Zhigang, Ding Fan, Jiang Xiaozhou, et al. New progress on community detection in complex networks [J]. Journal of National University of Defense Technology, 2011, 33(1): 47-52.

[4]Kernighan B W, Lin S. An efficient heuristic procedure for partitioning graphs[J]. Bell system technical journal, 1970, 49(2): 291-307.

[5]Pothen A, Simon H D, Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J]. SIAM Journal on Matrix Analysis and Applications, 1990, 11(3): 430-452.

[6]Capocci A, Servedio V D P, Caldarelli G, et al. Detecting communities in large networks[J]. Physica A: Statistical Mechanics and Its Applications, 2005, 352(2): 669-676.

[7]Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E, 2006, 74(3): 036104.

[8]Newman M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133.

[9]Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6): 066111.

[10] Girvan M, Newman M E J. Community structure in social and biological networks [J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826.

[11] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113.

[12] Fortunato S, Latora V, Marchiori M. Method to find community structures based on information centrality[J]. Phys Rev E, 2004, 70(5): 056104.

[13] Pan Y, Li D H, Liu J G, et al. Detecting community structure in complex networks via node similarity [J]. Physica A: Statistical Mechanics and Its Applications, 2010, 389(14): 2849-2857.

[14] 袁超, 柴毅. 基于簇相似度的网络社团结构探测算法[J]. 物理学报, 2012, 61(21): 539-547. Yuan Chao, Chai Yi. Group similarity based algorithm for network community structure detection [J]. Acta Phys Sin, 2012,61(21):539-547.

[15] 王兴元,赵仲祥.基于节点间依赖度的社团结构划分方法[J].物理学报， 2014， 63(17): 178901. Wang Xingyuan, Zhao Zhongxiang. Partitioning community structure in complex network based on node dependent degree [J]. Acta Phys Sin,2014,63(17): 178901.

(责任编辑 耿金花)

订 正

本刊2016年第13卷第1期第64页页脚基金项目中“国家统计科学研究项目(2015LZ497)”更正为“国家统计科学研究项目(2015LZ49)”；2016年第13卷第3期第33页页脚基金项目中“国家统计科学研究项目(2015LZ249)”更正为“国家统计科学研究项目(2015LZ49)”。

Finding Community Structure in Networks Using Node’s Dynamic Connection Degree

JIA Jun, HU Xiaofeng, HE Xiaoyuan

(a.The Department of Information Operation Command Training,b.The Department of Graduate,National Defense University,Beijing 100091,China)

This paper gives the definition of node’s dynamic connection degree at first, and then introduces the algorithm of finding the community structure by the node’s dynamic connection degree. After that, it analyzes the range of parameter’s value in node’s connection degree and proves it by experimenting on the Zachary network. On this basis, it experiments on three real networks which are dolphins, polbooks and football. The result proves that this algorithm can find different network’s community structure correctly by adjust its parameter’s value. At last, it compares the result with some other common algorithms’ and illustrates some matters that need attention.

node′s dynamic connection degree； community structure； finding community

10.13306/j.1672-3813.2016.04.008

2015-07-06;

2015-09-23

国家自然科学基金(U1435218, 61174035, 61273189, 61374179)

贾珺(1981-)，男，陕西西安人，博士研究生，助理研究员，主要研究方向为军事运筹学。

TP391.9

A