网络化分布式协作系统的最大同步

王付永，杨洪勇(鲁东大学信息与电气工程学院，山东 烟台 264025)

网络化分布式协作系统的最大同步

王付永，杨洪勇
(鲁东大学信息与电气工程学院，山东 烟台 264025)

基于网络化系统的拓扑结构特性，研究了分布式系统的最大同步问题。提出了一种应用个体局部信息的线性分布式控制协议。运用现代控制理论、代数图论和SIA等理论工具，对控制算法进行了稳定性分析，得到了网络化系统的最大同步收敛条件。最后应用仿真实验验证了所得结论的正确性。

网络化系统；最大同步；分布式控制；有向图；联合连通

0 引言

近年来，分布式多智能体协同控制系统在移动机器人编队、无人航天器的协同控制、卫星定位调姿和智能电网调度等军事和民用领域得到了广泛应用，逐渐成为控制理论、应用数学、计算机科学等领域研究的热点问题。分布式协作问题是多智能体或多机器人基于动态网络通过协调控制使其状态取得决策值，例如多智能体通过相互协调使得运动速度或运动方向趋于同步，或者到达同一集合点等。

网络化系统的一致性问题是分布式协同控制的一个重要研究方向[1-4]。所谓一致性是指随着时间的演化，自主体通过相互作用、相互协调使得系统运动达到同步。文献[5]研究了联合连通条件下一阶时滞多智能体系统的一致性问题，并采用Lyapunov-Krasovskii 泛函和矛盾分析法对系统进行了收敛性分析。在系统同时具有变时延和系统不确定性的情况下，文献[6]研究了一阶多智能体系统的鲁棒一致性问题。文献[7]研究了有向网络中固定拓扑和切换拓扑两种情况下一阶时滞多智能体系统的一致性问题，提出了具有不确定拓扑的平均一致性控制算法。文献[8]研究了具有时延和不确定拓扑的二阶多智能体系统的平均一致性问题，在通信拓扑为联合连通的情况下，利用Lyapunov-Krasovskii方法，以线性矩阵不等式的形式给出了系统达到平均一致性的充分条件。文献[9]研究了二阶连续多智能体系统的一致性问题，利用离散化和状态变换的方法，将一致性问题转化为了一系列矩阵的Schur稳定性问题，并得到了一致性成立的充要条件。文献[10]研究了具有通讯时延的分数阶多智能体系统的一致性问题，应用分数阶系统的Laplace变换和频域理对系统进行了收敛性分析。

在某些实际应用中，如最小时间交会、最优目标跟踪、寻找最优路径等，一类特殊的一致性问题，即最大一致性问题，引起了人们的关注。在这种情况下，如果系统中所有成员最终都能达到同一状态且为初始最大状态，则称系统能够实现最大一致性。文献[11]针对动态多智能体系统的一致性问题，提出了一族单参数的有界分布式一致性算法，其算法包含了平均一致性和最小一致性两种特殊的一致性算法。文献[12]针对离散时间多智能体系统的一致性问题，提出了最大一致性控制算法，并利用max-plus代数的方法分析了算法的收敛性。文献[13-14]分别研究了时间相关和状态相关的多智能体系统的一致性问题，提出了一种结合平均一致性和最大一致性的广义一致性控制算法。本文研究有向拓扑下网络化系统的最大同步问题，本文与前面文献不同之处在于提出了一种基于个体局部信息的分布式动态控制算法，应用代数图论和SIA等理论工具，分析了有向网络拓扑下分布式多智能体系统的最大一致性算法的收敛问题。

1 数学描述

设G=(V,E,A)是n个结点的权重有向图，V={v1,v2,…,vn}为一个顶点(或结点)集合，E⊆V×V为一个边的集合，A=[aij]为权重邻接矩阵，其中eij=(vi,vj)∈E，vi,vj∈V；对于∀i,j∈I={1,2,…,n}:i≠j,aij≥0；对于∀i∈I,aii=0。结点vi的邻接集合定义为Ni={j∈I:aij≥0}。定义D=diag{d1,d2,…,dn}∈Rn×n为图G的度矩阵，其中di=∑j∈Niaij，i=1,2,…,n。权重图G的Laplacian矩阵定义为

L=D-A∈Rn×n

(1)

由定义可知，1n是L零特征根的一个右特征向量。图G的一条长度为N的道路是一个不同顶点{v1,v2,…,vN+1}的有序集合，且∀i∈[1,N],(vi,vi+1)∈E。一个有向图G称为是强连通的，当且仅当图G的任意两个不同的顶点之间有一条有向通道。进一步，如果G为强连通的，则rank(L)=n-1[15]。

设x=(x1,x2,…,xn)表示所有结点的状态，且满足下面微分方程：

(2)

假设χ:Rn→R为x的函数，其值y=χ(x)称为决策值，其中最大同步决策值满足

χ(x)=Max(x)=Max{x1,x2,…,xn}

(3)

图的所有结点在有限时间T>0关于χ取得了协同一致，当且仅当所有结点两两满足xi(T)=χ(x(0)),∀i∈I。

定义1[16]树为一种特殊的图，除了根结点外，每个结点仅有一个父结点。如果一个图的生成子图是树，称该子图为生成树。

定义2[17]令Mn(R)表示所有n阶实方阵的集合，如果矩阵A∈Mn(R)的所有元素均非负，则称矩阵A为非负矩阵，记为A≥0。一个非负矩阵，如果其行和为+1，称其为(行)随机矩阵。一个随机矩阵P，如果满足limn→∞Pn=1nyΤ，其中y为某个列向量，1n=(1,1,…,1)Τ，则称随机矩阵P为非周期不可分的(SIA)。

定义3[18]设拓扑图Tri=0与联合图G=G1∪G2∪…∪Gm具有相同的顶点集V；联合图G的边集为所有图G1,G2,…,Gm边集的并，边的连接权重是对应的链接权重之和。如果它们的联合图G是连通的，则称G1,G2,…,Gm为联合连通的。

2 分布式网络化系统的最大同步

基于有向网络拓扑，考虑一个由n个智能体构成的一阶网络化系统，其动态方程描述为

(4)

其中xi(t)∈R,ui(t)∈R分别为第i个智能体的状态和控制输入。本文研究一阶网络化系统的最大同步问题，假设其控制协议为

(5)

其中，αij(选择系数)的取值满足如下定义：

(6)

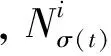
引理1[17]如果一个有向图的集合{Gt1,Gt2,…,Gtm}的并存在一棵生成树，则矩阵积e-LtmΔtm…e-Lt2Δt2e-Lt1Δt1为SIA的，其中Ltd为对应于每个有向拓扑图Gtd的Laplacian矩阵，Δtd>0,d∈{1,2,…,m}。

引理3连续时间网络化系统(4)-(5)当t→∞时取得渐近同步，当且仅当

(7)

其中，I表示单位矩阵，1n表示分量均为1的n×1列向量，y为一个n×1常向量，Φ(t,0)表示系统转移矩阵，-L(σ1),-L(σ2),…表示系统在σ1,σ2…时的系数矩阵。

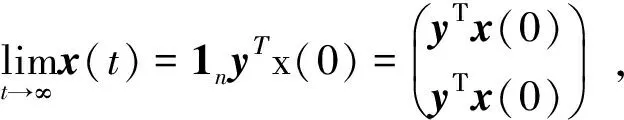
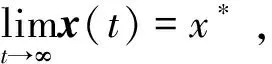
分析：本文研究具有固定拓扑的网络化系统，由于控制协议中参数αij的动态变化，造成了系统局部拓扑结构的动态变化，这样就不能保证有向网络为时不变的。为了更好地解决这一问题，我们引入了联合连通的概念及其相关理论。

证明：根据上述分析，可知在有限个不重叠的时间间隔[tr,tr+1)内的通信拓扑结构保持不变。令σ(t)[0,∞)→{1,2,…,m}是一个切换信号，m为总拓扑数. 记系统通信拓扑图为Gσ(tr)，且Gσ(tr)相应的Laplacian矩阵用Lσ(tr)表示。

系统在时间段[tr,tr+1)内的动态方程可表示为

(8)

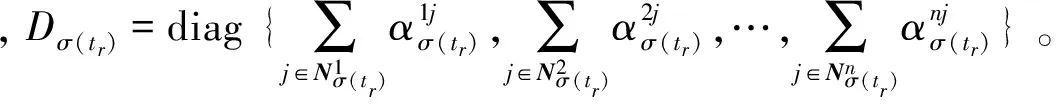
x(1)=e-Lσ(t1)Δt1x(0)，x(2)=e-Lσ(t2)Δt2x(1),…,x(m)=e-Lσ(tm)Δtmx(m-1)

(9)

即有：

x(m)=e-Lσ(tm)Δtm…e-Lσ(t2)Δt2e-Lσ(t1)Δt1x(0)

(10)

其中，Δtd=td+1-td,d=1,…,m。

下面讨论各智能个体与其邻接成员关系的不同情形，并定性分析各种情况下各智能个体的动态特性：

1)当智能体i的邻域内任意智能体j的状态xj均不大于其状态xi时，由αij的定义可知αij=0，则有

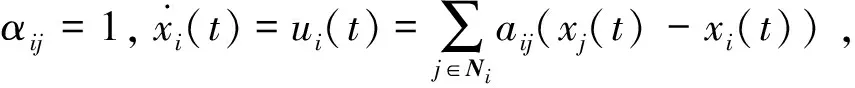
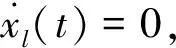
注1：状态转移矩阵具有性质Φ(tm,t0)=Φ(tm,tm-1)Φ(tm-1,tm-2)…Φ(t1,t0)，Φ(tr+1,tr)=e-Lσ(tr)Δtr，

注2：本文结论是基于强连通的有向网络，对于一般的有向网络该结论并不一定成立。尽管基于有向拓扑的所有智能体组成的通信拓扑图集合的并存在一颗生成树，并不能保证其生成树的根节点为网络化系统的全局最大状态，即不能保证所有智能体取得全局最大同步。 假定有向网络为强连通的，则能够使网络化系统的全局最大状态作为生成树的根节点，也就保证了所有智能体取得了全局最大同步。

注3：基于有向切换网络，由若干智能体构成的连续时间网络化系统取得最大同步的充分条件为系统拓扑图的集合在整个有限时间区间内为联合强连通的。

推论1设t1,t2,…,tm为一个有限的时间序列，拓扑图G(t)、权重因子aij(t)和选择系数αij(t)在时间序列t1,t2,…,tm这些时间点切换。如果存在一个一致有界、不相重叠的时间区间的有限序列[tr,tr+1),r=0,1,…,m，t0为初始时刻，且有向图的集合{Gi1,Gi2,…,Gim}⊂G在区间[t0,tm]联合强连通，则基于动态切换网络的连续时间网络化系统取得最大渐近同步。

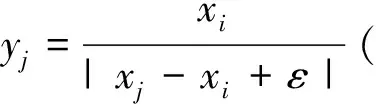
3 实例分析

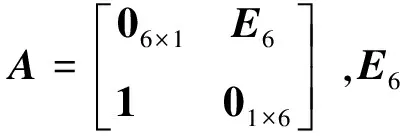
针对动态切换拓扑，考虑如下互连拓扑图。图3的4个互连图均为非连通的，均不存在生成树，但它们的并为强连通的，且存在着一棵生成树。系统的拓扑在图3中的4个子拓扑下切换，各智能体的初始状态取为x(0)=[54 686.57]。假定互连拓扑图在时刻t=kT,k=0,1,…,在图4集合中随机地切换，T取为0.5秒。图5为系统在15秒计算机仿真时间内的运动轨迹，其中采样间隔为0.1s。可见基于有向切换网络，各智能体的状态渐近收敛到了其状态最大值，即取得了全局最大同步。

4 结论

本文提出了一种应用个体局部信息的分布式控制算法，在控制器中引入了动态参数，有效地解决了有向网络的全局最大同步问题。基于固定拓扑的强连通有向网络，具有动态参数的控制协议保证了分布式系统的全局最大同步。有向拓扑网络化系统的强连通性及控制器动态参数的设计是系统实现收敛性的关键。二阶系统及时滞拓扑情形有待进一步研究。

[1]Dai P P, Liu C L, Liu F. Consensus problem of heterogeneous multi-agent systems with time delay under fixed and switching topologies[J]. International Journal of Automation and Computing, 2014, 11(3): 340-346.

[2]Diao M, Duan Z S, Wen G H. Consensus tracking of linear multi-agent systems under networked observability conditions[J]. International Journal of Control, 2014, 87(8): 1478-1486.

[3]Jiang Y L, Liu J C, Wang S Q. Cooperative output feedback tracking control for multi-agent consensus with time-varying delays and switching topology[J]. Transactions of the Institute of Measurement and Control, 2015, 37(4): 550-559.

[4]Sakurama K, Nakano K. Necessary and sufficient condition for average consensus of networked multi-agent systems with heterogeneous time delays[J]. International Journal of Systems Science, 2015, 46(5): 818-830.

[5]Lin P, Jia Y. Multi-agent consensus with diverse time-delays and jointly-connected topologies[J]. Automatica, 2011, 47(4): 848-856.

[6]曾耀武，冯伟. 具有时滞和不确定性多智能体鲁棒一致性研究[J]. 复杂系统与复杂性科学，2013，10(3)：75-80. Zeng Yaowu, Feng Wei. Robust consensus analysis of milti-agent systems with both time-delay and uncertainty[J]. Complex System and Complexity Science, 2013, 10(3), 75-80.

[7]Shang Y. Average consensus in multi-agent systems with uncertain topologies and multiple time-varying delays[J]. Linear Algebra and Its Applications, 2014, 459: 411-429.

[8]宋莉，伍清河. 具有时延和不确定拓扑的二阶多智能体系统的平均一致性[J]. 控制理论与应用，2013，30(8)：1047-1052. Song Li, Wu Qinghe. Average consensus of second-order multi-agent systems with time-delays and uncertain topologies[J]. Control Theory & Applications, 2013, 30(8): 1047-1052.

[9]高彦平，姜同强，王雯,等. 二阶多智能体系统的一致性分析[J]. 复杂系统与复杂性科学，2014，11(4)：87-91. Gao Yanping, Jiang Tongqiang, Wang Wen, et al. Consensus analysis of second-order multi-agent systems[J]. Complex System and Complexity Science, 2014, 11(4), 87-91.

[10] 杨洪勇，徐邦海，刘飞,等. 分数阶多智能体系统的时延一致性[J]. 复杂系统与复杂性科学，2013，10(3)：81-85. Yang Hongyong, Xu Banghai, Liu Fei, et al. Consensus of fractional-order multi-agent systems with communication delay[J]. Complex System and Complexity Science, 2013, 10(3), 81-85.

[11] Tahbaz-Salehi A, Jadbabaie A. A one-parameter family of distributed consensus algorithms with boundary: From shortest paths to mean hitting times[C]∥ 2006 45th IEEE Conference on Decision and Control, San Dlego,CA,VSA. 2006: 4664-4669.

[12] Nejad B M, Attia S A, Raisch J. Max-consensus in a maxplus algebraic setting: The case of fixed communication topologies[C]. Int Symposium on Information, Communication and Automation Technologies, Sarajevo,Bosnia and Herzegovina.2009:1-7.

[13] Shi G, Johansson K H. Convergence of distributed averaging and maximizing algorithms part I: time-dependent graphs[C]. 2013 American Control Conference (ACC) Washington, DC, USA,2013.

[14] Shi G, Johansson K H. Convergence of distributed averaging and maximizing algorithms part II: state-dependent graphs[C]. 2013 American Control Conference (ACC) Washington, DC, USA, 2013.

[15] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9):1520-1533.

[16] Godsil C D, Royle G, Godsil C D. Algebraic Graph Theory[M]. New York: Springer, 2001.

[17] Ren W, Beard R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.

[18] 王芳，陈鑫，何勇，等. 联合连通条件下的二阶多智能体系统有限时间一致性控制[J]. 控制理论与应用，2014，31(7)：981-986. Wang Fang, Chen Xin, He Yong, et al. Finite-time consensus control of second-order multi-agent systems with jointly-connected topologies[J]. Control Theory & Applications, 2014, 31(7): 981-986.

(责任编辑 李进)

Maximum Synchronization of Networked Systems with Distributed Collaboration

WANG Fuyong, YANG Hongyong

(School of Information and Electrical Engineering, Ludong University, Yantai 264025,China)

Based on the topology feature of networked systems, maximum synchronization of distributed systems is studied. A distributed control protocol with individual′s local information is proposed. By using theoretical tools of modern control theory, algebraic graph theory and SIA, the stability of control algorithm is analyzed. The convergence condition of the maximum synchronization for networked systems is achieved. Finally, simulation examples are given to verify the correctness of the conclusion.

networked systems; maximum synchronization; distributed control protocol; directed graph; jointly-connected

10.13306/j.1672-3813.2016.04.009

2015-01-28；

2015-09-17

国家自然科学基金(61273152,61304052,51407088)；山东省自然科学基金(BS2015DX018)

王付永(1990-)，男，山东济南人，硕士研究生，主要研究领域为复杂网络、多智能体编队控制。

杨洪勇(1967-)，男，山东德州人，博士，教授，主要研究领域为网络应用技术、多智能体编队控制、复杂网络控制、非线性系统控制等。

TP27

A