基于关联分布函数的相互依赖网络脆弱性分析

金伟新，宋 凭，刘国柱(.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 47003；2.国防大学信息作战与指挥训练教研部，北京 0009； 3.西安通信学院军事通信指挥系，西安 7006)

基于关联分布函数的相互依赖网络脆弱性分析

金伟新1,2，宋 凭1,3，刘国柱1
(1.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003；2.国防大学信息作战与指挥训练教研部，北京 100091； 3.西安通信学院军事通信指挥系，西安 710106)

首先综述了国内外互依网络级联脆性的研究现状，分析目前研究取得的成果与问题，而后在此基础上，针对目前研究的薄弱环节——互依网络之间的关联机制与关联机理进行了深入分析与重点研究，构建了基于关联分布函数的相互依赖网络脆弱性分析模型，并给出了互依网络脆弱性评估的六类判据。最后，给出了研究结论与建议。

互依网络；级联失效；脆弱性；模型

0 引言

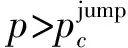
由此可见，对于互相依赖网络的脆弱性分析，其主要研究内容包括：1)互依网络各构成网络自身拓扑结构及其动力学特性；2)互依网络相互依赖关联结构及其动力学特性；3)互相依赖“网络的网络”的拓扑特征及其动力学特性。

我们认为，对互依网络脆弱性的研究，相对于其他部分研究而言，互依网络之间依赖、关联关系拓扑结构及其动力学性质的分析、研究最为关键。而比较而言，综述目前的研究进展，这一部分的研究也是极其薄弱的部分。

鉴于此，论文重点对互依网络相互依赖、关联的网络间的连接、依赖结构的拓扑模型及其动力学特性进行建模分析，尝试推进目前互依网络脆弱性研究局限于耦合强度、一对一连接等过于简化的、与现实互依网络差异较大的“衡同”依赖等均质化假设，构建与实际依赖、连接多样化关系一致的多样化连接、依赖网络模型；在此基础上，形成脆弱性分析结果与结论。

1 基于关联分布函数的相互依赖网络脆弱性建模

为了描述互依网络的关联特征，用图1给出3个互依网络A、B、C的内部连接与外部依赖关系。由图1可以看出，互相依赖网络节点之间的关系包含两类：同网络内部节点之间的连接关系与不同网络节点之间的依赖关系。依赖关系是有向的。两个网络可以互相依赖，比如因特网与电力网。

由此可见，互依网络节点之间的关联关系至少存在两种不同类别，采用传统单一变量度分布函数很难给出准确描述。如何做到既能表现网内之间的连接，又能描述不同网络之间的依赖关系，联合概率分布函数模型可能是互依网络脆弱性分析建模的首选模型。但这一点，在过去的研究中并没有获得很好的关注和重视。

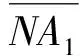
网络A节点i与网络B节点j各类连接、依赖关系如图2。

假设由A网络与B网络共同构成的互相依赖的大网络为Q网络，其节点i的度概率分布函数为pQ(x，y，z)，其中x是同网络内部连接度、y是各网络指向其他网络的出度(被依赖连接)、z是其他网络指向它的连接入度(依赖连接)。Q网络节点集合分别为N，该集合节点总数为n。

基于上述假设，可得：

N=NA∪NB

(1)

n=nA+nB

(2)

(3)

(4)

(5)

(6)

至此，可以给出节点i的度概率分布函数pQ(x,y,z)的计算模型。

对于网络A，不同节点集度联合概率分布函数分别为

(7)

(8)

(9)

(10)

同理，对于网络B，不同节点集度联合概率分布函数分别为

(11)

(12)

(13)

(14)

基于网络与概率理论，不难推得式(15)：

(15)

在得到连接、依赖关联的度联合概率分布函数后，可以运用生成函数方法对互依网络因故障或遭攻击后其最大互联组件，即分裂后的最大互联子网络)的规模和分裂组件(分裂的互联子网络)的平均规模及其临界阈值条件进行建模，并作出分析，获取有价值的结论。

对于网络A，其各集合节点对应的联合度概率分布生成函数分别为

(16)

(17)

(18)

(19)

同理，对于网络B，其各集合节点对应的联合度概率分布生成函数分别为

(20)

(21)

(22)

(23)

从而，在相依网络的A网络(或B网络)任选一条边，该边将会是如下3种不同类别的边之一：A网络(或B网络)内部节点互连的边；A网络(或B网络)指向B网络(或A网络)的边(B依赖A的边)；B网络(或A网络)指向A网络(或B网络)的边(A依赖B的边)。这3种不同的边抵达节点的度概率分布生成函数分别为

对于A网络，

(24)

(25)

(26)

同理，对于B网络，

(27)

(28)

(29)

基于此，可以推导互依网络A或B某一节点因故障或攻击失效后，因为连接、依赖级联引发连锁失效，进入稳定态后，Q最大互联组件(族)规模S及破碎组件的平均规模〈s〉。

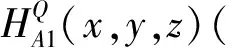
(30)

(31)

(32)

(33)

(34)

(35)

(36)

由此得，攻击A网络节点或A网络节点发生故障后，网络裂解后互联组件的平均规模〈s1〉为

(37)

再由(30)可得：

(38)

所以，有式(39)成立：

(39)

同理，由(31)、(32)可以推得：

(40)

(41)

将(16)～(19)、(39)～(41)式代入式(37)，得：

(42)

同理可得，攻击B网络节点或B网络节点发生故障后，网络裂解后互联组件的平均规模〈s2〉为

(43)

由此可见，只要以下条件任何一项得到满足，式(42)、(43)就会发散，由A、B网络构成的互依网络就会瘫痪，这说明互依网络较之于单一网络，其脆弱性表现更加多样化，倘是这些脆弱点遭遇攻击，都可能致整体网络失能。

这些条件是：

(44)

(45)

(46)

(47)

(48)

(49)

但上述条件达成，是针对互依网络的不同区域进行的：(44)、(47)主要针对互依网络各网络自身连接，而(45)、(48)重点在于依赖连接关系，(46)、(49)重点在被依赖关系。实际运用时，可以视攻击或防御的成本、难度单独或综合实施，提高或加强互依网络的攻击或防御效果。

2 基于关联分布函数的相互依赖网络脆弱性模型分析

当将式(24)～(29)分别代入式(44)～(49)，可以获得更清晰的互依网络脆弱性分析判据。

当将式(24)、(27)分别代入式(44)、(47)时，分别获得以下判据：

(50)

(51)

这就是我们在单一网络脆弱性分析时获得的判据，此时A、B网络各自已经瘫痪。

当分别将(25)、(26)、(28)、(29)代入(45)、(46)、(48)、(49)时，便得到了互依网络相互依赖的脆弱性判据，而这一点在单一网络的脆弱性分析时是不能获取的。这些判据为

(52)

(53)

(54)

(55)

尽管推导过程复杂，但上述判据的形式是简洁的。上述判据表明，互依网络的脆弱性主要取决于互依网络度关联分布函数的一阶矩与二阶矩，这为我们采用何种关联结构设计以利于改善互相依赖网络的鲁棒性提供了理论指导和数据支持。

3 实例分析

为了探索不同关联分布函数对互依网络脆弱性的影响，在复杂系统仿真平台Netlogo上开发了由指控网络、情报网络、作战网络和通信网络4类互相依赖网络构成的体系网络脆弱性分析软件，对不同关联分布函数对体系网络的脆弱性影响进行了建模与仿真分析。军事上，体系网络是通过通信网络将其构建、连接为一个可动态组构的整体。我们设计的关联分布函数为幂律分布与波松分布混合的复合分布函数，这符合大多现实网络的实际。

(56)

其中，α、x、y、z分别表示两类分布的混合比、通信节点网内连接度与网间连接出度和连接入度。当α= 0时，表示关联分布为幂律分布；当α= 1时，表示关联分布为波松分布。

对于波松分布，由于

(57)

(58)

(59)

(60)

其中，λ1、λ2、λ3分别为通信节点网内连接平均度与网间连接平均出度和平均入度，其仿真生成使用ER算法。

对于幂律分布，由于

(61)

(62)

(63)

(64)

其中，m1、m2、m3分别为通信节点网内连接最小度与网间连接最小出度和最小入度，γ1、γ2、γ3分别为通信节点网内连接度分布与网间连接出度和入度分布标度指数，其仿真生成使用BA算法。

运用已开发的基于关联分布函数互相依赖的体系网络脆弱性分析仿真平台，对α= 1、α= 0、α= 0.5三种不同混合比的体系网络，分别使用基于关联分布函数的度优先攻击与基于常规指控、传感节点优先攻击方法，对体系网络进行攻击，获得了下列仿真结果。

当α= 1时，攻击前、后体系网络拓扑演化如图3所示，基于关联分布函数的度优先攻击与基于常规指控、传感节点优先攻击失联连边与失联节点数值曲线如图4所示。

当α= 0时，攻击前、后体系网络拓扑演化如图5所示，基于关联分布函数的度优先攻击与基于常规指控、传感节点优先攻击失联连边与失联节点数值曲线如图6所示。

当α= 0.5时，攻击前、后体系网络拓扑演化如图7所示，基于关联分布函数的度优先攻击与基于常规指控、传感节点优先攻击失联连边与失联节点数值曲线如图8所示。

由以上仿真结果比对分析不难发现，无论α= 1、α= 0或α= 0.5何种情形，较之基于非关联分布函数的攻击方法，基于关联分布函数的度优先攻击对相互依赖的体系网络的毁伤效果都极为显著，其中α= 0最显著，其次α= 0.5，再次α= 1。

4 结果与结论

论文提出了基于关联分布函数的互依网络脆弱性建模与分析方法，并理论推导了基于关联分布函数的互依网络脆弱性判定的临界条件；通过仿真实验，基于关联分布函数的度优先攻击相比较于非关联分布函数的攻击方法，攻击效果更显著。对于由幂律、波松分布构成的混合关联分布函数，在混合比α= 0时，互依网络最脆弱，其次α= 0.5，再次α= 1。

上述研究给我们提供的启示是：对于互相依赖网络的脆弱性研究，我们需要重点关注互相依赖、互相关联连接的内部结构的精细分析。在两个互相依赖网络的互相依赖、交互的毗连区、关联部位可能发现和揭示互依网络的关联机制、结构脆性与动力学特征。我们下一步工作将结合不同关联分布函数的设计，研究互相依赖网络在不同攻击策略下的级联动力学脆弱性的传播模式和机理。

[1]Helbing D. Globally networked risks and how to respond[J]. Nature , 2013,497:51-59.

[2]Vespignani A. The fragility of interdependency[J]. Nature ,2010,464:984-985.

[3]Buldyrev S V, Parshani R ,Paul G,et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010 ,464:1025-1028.

[4]Parshani R, Buldyrev S V, Havlin S.Interdependent networks:reducing the coupling strength leads to a change from a first to second order percolation transition[J]. Physical Review Letters, 2010,105(4): 048701.

[5]Bashan A, Parshani R, Havlin S. Percolation in networks composed of connectivity and dependency links[J]. Physical Review E ,2011,83(5):051127.

[6]Shao J, Buldyrev S V, Havlin S,et al. Cascade of failures in coupled network systems with multiple support-dependence relations[J]. Physical Review E,2011,83(3):036116.

[7]Schneider C M,André A,Andrade M S,et al. Mitigation of malicious attacks on networks[J]. PNAS ,2011,108(10) :3838-3841.

[8]Gao J, Buldyrev S V, Stanley H E ,et al. Networks formed from interdependent networks[J]. Nature Physics,2012,8:40-48. http: // www.nature.com/naturephysics.

[9]Li W, Bashan A, Buldyrev S V,et al. Cascading failures in interdependent lattice networks:the critical role of the length of dependency links[J]. Physical Review Letters,2012,108(22):228702.

[10] Gao J, Buldyrev S V, Havlin S,et al. Robustness of a network formed by n interdependent networks with a one-to-one correspondence of dependent nodes[J]. Physical Review E,2012, 85(6):066134.

[11] Dong G, Gao J, Jin R,et al. Robustness of network of networks under targeted attack[J]. Physical Review E ,2013,87: 052804.

[12] Zhou D, Gao J, Stanley H E ,et al. Percolation of partially interdependent scale-free networks[J]. Physical Review E ,2013,87(5):052812.

[13] Hu Y, Zhou D,Zhang R,et al. Percolation of interdependent networks with intersimilarity[J]. Physical Review E, 2013,88(5):052805.

(责任编辑 耿金花)

The Analysis for the Vulnerability of the Interdependent and Interconnected Network of Networks Based on the Correlation Degree Distribution Functions

JIN Weixin1,2，SONG Ping1,3，LIU Guozhu1

(1.The State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System(CEMEE),Luoyang 471003, China;2.The Information Operations and Command Training Department, National Defense University,Beijing 100091,China;3.The Military Communication Comand Department, Xi’an Communication Institute,Xi’an 710106,China)

In this paper, research status quo on the cascading vulnerability of interdependent networks is reviewed firstly. Secondly,its progress and unsolved problem are analyzed.Based on this,the blind area of the present interdependent networks vulnerability research—correlation mechanism and correlation principle of interdependent networks are deeply analyzed and studied,and the vulnerability analysis models which based on the correlation degree distribution functions are built,at the same time,six criteria of interdependent networks vulnerability evaluation are summed up.Lastly,the conclusion and proposal are put forward.

interdependent and interconnected networks;cascade failure; vulnerability; model

10.13306/j.1672-3813.2016.04.002

2014-05-30；

2014-09-13

CEMEE国家实验室开放课题基金(CEMEE2014K0201A)；国家自然科学基金(60974080)

金伟新(1963-),男，河南光山人，副教授，大校，主要研究方向为相互关联与相互依赖网络脆弱性、复杂系统建模与仿真。

N94

A