网络的安全域方法及与抗毁性的对比验证

肖 峻, 苏步芸, 李 鑫, 王成山 (.天津大学智能电网教育部重点实验室，天津 0007；.中国能源建设集团广东省电力设计研究院有限公司，广州 5066；.国网四川省电力公司电力科学研究院，成都 6007)

网络的安全域方法及与抗毁性的对比验证

肖 峻1, 苏步芸2, 李 鑫3, 王成山1
(1.天津大学智能电网教育部重点实验室，天津 300072；2.中国能源建设集团广东省电力设计研究院有限公司，广州 510663；3.国网四川省电力公司电力科学研究院，成都 610072)

为网络遭受外部攻击或内部失效后的安全性分析和预防措施研究提供了新方法，该方法描述网络在N-1安全约束下的安全运行区域，并通过工作点到域边界的距离反映出安全或不安全的程度，为下一步控制措施指示了方向和强度。本文将安全域的方法应用在不同规模的一般网络、通信网和电网中，验证了方法的普适性和有效性；并与抗毁性对比，结果表明本文方法与抗毁性具有较高一致性，且计算速度更快，适合于在线安全监视与控制，以提前消除隐患。

安全域；N-1 边界；安全距离；抗毁性

0 引言

安全、可靠和高效是系统追求的目标。各种现实中的网络[1-3]在因外部随机扰动或恶意攻击导致某些元件失效时，都需要保持一定的功能。抗毁性是评价这种功能的一个典型方法和指标，近十年来得到了广泛的研究和应用。

抗毁性的研究始于战略通信网，后因2000年Albert等人在《Nature》杂志发表论文[4]后，迅速成为网络可靠性研究的一个重要分支。网络抗毁性指在网络元件发生失效时网络维持其功能的能力[5]，其在社交网[6]、Internet[7]、通信网[8]、电力网[9]都得到了应用，特别是由多种网络组成的相依网络抗毁性[10-11]研究，成为近年来复杂网络研究的一个热点。抗毁性的研究经历了由纯拓扑的静态抗毁性[4]到级联失效动态抗毁性[12]的过程，在负载重分配方式[13]、权值分配[14]、节点重要度[15]研究方面逐步完善，对优化网络增强其鲁棒性[16]有很大应用潜力。

抗毁性作为一个评价网络可靠性的重要指标，反映了网络承受攻击的能力，同时在现实中，人们在网络元件失效后，往往对这种承受能力有一定的要求，例如电网普遍采用了N-1安全准则，即一个元件失效(N-1)后应对除故障段外其它所有负荷持续供电[17]。本文发现，若明确N-1后的要求，则可以事先得到一个运行区域，只要在域内运行，发生元件失效后一定能达到预设要求，称该区域为“网络的安全域”。安全域在整个状态空间中描述了网络可安全运行的区域。若能得到安全域边界，运行人员就能在系统状态位于边界外时提前采取措施，避免故障发生后网络大面积出现问题，而且能在保持一定裕度下将系统运行到接近边界的位置，最大限度地发挥系统效率。

安全域源自电力系统，最早于1975年出现在E.Hnyilicza和S.T.Y.Lee等对电力网静态安全性的研究中[18]。近二十年来，以中国余贻鑫院士为代表的研究者在输电网安全域领域取得了一系列重要成果，包括安全域模型[19]和安全域方法学[20]，并在国内外实际电网的安全预警、 控制与风险分析中得到了成功应用[21-22]，被认为是未来避免电网大规模停电很有希望的一项技术。

目前安全域理论除在电力系统外并未真正推广至其它领域。有学者尝试将其应用到轨道交通系统，给出了交通系统安全域初步的思路[23]，但仅仅局限于框架性的研究。通信网的容量域运用了域的思想确定网络容量[24]，但并未涉及元件失效问题。电力系统的安全域未推广的主要原因源自输电系统的复杂性。输电系统除考虑网络一般特征外，还需要考虑各种复杂的稳定问题[20]，导致其模型描述非常复杂，涉及到大量非线性微分方程，模型通用性较差，阻碍了该理论在其它领域中的应用。

近年来在配电自动化背景下[25]，配电网安全域(Distribution System Security Region，DSSR)的提出为安全域推广到电网外提供了可能。文[26]仿真发现安全和不安全工作点的分界现象，研究了DSSR边界的拓扑性质[26], 文[27]提出了DSSR的定义和模型。DSSR正成为智能配电网运行的核心技术[28]。配电网更接近一般网络，本文在其基础上针对计及容量流量的网络模型，提出安全域的定义及解析模型，分别在小型网络和大规模网络上进行了验证，并与抗毁性结果对比，体现了安全域其独特的优势以及在评价网络可靠性上与抗毁性的一致。

1 安全域的定义

网络用无向连通图G=(V,E)表示，节点数为M=|V|，边条数为N=|E|，V={vl,v2,v3，…,vM}为节点集合，E={el,e2,e3，…,eN}为边的集合，V中每条边都有E中一对节点对应。(vi,vj)表示由vi到vj的一条边。本文研究是基于边失效，视节点容量为无穷大，边的容量cij定义为可通过边的最大允许流量值，边的流量fij表示边上的实际流量值，也称为边的负载。

1.1 负载重分配策略

当网络中一个元件失效后，负载需要重新分配[12]，重分配策略描述了N-1后网络的工作过程，是N-1安全分析的基础。不同网络传递对象不同，所以再分配策略也可能不同。通信网常采用多径路由策略[29]，即一条边失效后会有多条可分配路径，见图1a。所有路径故障前都处在运行状态，存在备用冗余容量。电力网常采用最近邻负载重分配策略[12]，如图1b所示，即边失效后，负载根据与之直接相连接节点度的信息以一定的比例分配到最近邻的边上，实现负载的重分配。

1.2 N-1安全性定义

定义1网络的工作点(简称工作点)：表示在某一时刻或状态下，网络所有边的状态向量及运行方式。最典型的状态向量是流量，包括边的流量以及全网的总流量。运行方式指网络中节点和边的连通状态，例如网络中开关量的状态。

网络的工作点用边流量组成的N维欧式空间向量表示，N为边的个数，i和j为节点，定义如式(1)。

(1)

Z中元素是网络中所有边的流量值，共有N个元素，元素没有限定的排列顺序。

定义2单条边的N-1安全性：当在某个工作点运行时，移去某条边，网络能通过负载重分配以保持预设规定的流量传送，此时所有边的流量不超过其容量(不过载)。则网络在该工作点下，对该边是N-1安全的，否则是不安全的。以此类推，可定义元件集乃至网络的N-1安全性。

定义3网络的N-1安全性：当在某个工作点运行时，移去网络中的任意一条边，网络都能通过负载重分配以保持预设规定的流量传送，此时所有边的流量不超过其容量(不过载)。若在某个工作点满足上述条件，则称为网络在该工作点下是N-1安全的，否则是不安全的。

例如，对于电力网，N-1之后需要维持负荷点能够正常得到能源的网络功能，表现为负荷能够正常被供电；对于通信网，必须维持信息能够无差错正常传输的网络功能，需要存在迂回路径，表现为通信不中断。

同样地，还可以定义网络的N-X安全性，即同时移去网络中的多条边或节点的情况。

1.3 安全域的定义

域来源于数学中约束集的思想，域的元素可以是空间中的点、向量或者矩阵等[30]。例如在优化设计中，域为满足不等式约束方程的设计变量的集合[31]；通信系统的容量域为全体速率组所组成集合的凸闭包(即线性组合)[24]；域在输电力系统中表现为满足潮流方程和其它约束的工作点集合[20]。而本文中的安全域是网络满足N-1安全约束工作点的集合。

定义4网络的安全域(Secure Region，SR)：拓扑和容量确定的网络在运行过程中，满足网络N-1或N-X安全约束的工作点的集合。该集合在状态空间中具有唯一确定的边界，位于边界内和边界上的所有工作点都是安全的；位于边界外的所有工作点都是不安全的。

需要指出，该定义包括了N-X，但后文的模型和算法仅限于N-1这种最基本的情况，也未计及N-1后可能引起的级联失效。原因有二：1)同时多个元件失效的N-X，其发生概率相对很小，可在N-1基础上扩展；2)至于N-1后可能引起的级联失效，很多网络采取过载控制措施避免级联失效的产生，如电网的切负荷控制[32]、交通网的拥塞控制[33]、通信网的拥塞控制[34]等。因此本文选择首先解决N-1的问题。

2 安全域的模型

2.1 模型的适用范围与假设条件

模型适用于有容量和流量的无向网络，模型假设：

1)基于边的容量和边失效，未考虑节点的容量约束，因为节点失效后相邻边都不可用，所以节点失效等效为边失效的N-X。

2)对随机失效和故意攻击两种失效模式都适用，失效后的负载重分配策略见3.1节。

3)网络流量分布满足一定的自然规律，本文假设流量传输方程是线性的，即流量分配可进行简单加减运算。

4)实际网络存在流量损耗。本文为突出主要问题，近似认为是无损传输的。

2.2 模型的一般形式

用W(fij)≤0表示N-1安全约束，安全域是满足N-1安全约束的所有工作点的集合，其模型的一般形式为

(2)

其中，Z是式(1)定义的工作点；V为边的集合。式(2)安全域既可通过解析方法得到，也可以通过搜索工作点进行N-1仿真寻找域边界，以下采用解析方法。

2.3 模型的解析形式

将N-1安全约束具体化为要求N-1后网络不损失流量。在正常工作时各边流量应小于容量，得到N个约束；断开任意一条边(N-1)后进行一次负载重分配，分配后仍要求各边流量小于容量，又得到N个约束，共2N个约束条件，于是安全域的表达式为

(3)

其中，Bij表示fij失效后负载重分配涉及到的路径。对于通信网等信息类网络，Bij指失效边上负载重分配所经过迂回路由上所有边的集合。对于电力网等能源网，Bij指负载重分配引起流量改变边的集合。hmn是一个小于等于1的数，表示负载fij分配到边(vm,vn)上的比例，若重分配路径只有一条，则hmn=1。

域边界是描述域的关键，本文通过解析方式描述安全域的边界方程：

(4)

式(4)为一组边界，其围成区域是安全域。若网络流量传输方程是线性或近似线性的，则边界可以用超平面表示，将大大简化域的计算。因此本文边界用超平面来表示。

定义5边的安全距离：工作点到安全边界即各超平面的距离。即为

(5)

若式(5)中Dij大于等于0，说明边(vi,vj)发生N-1故障后，重分配可以保证所涉及的边集合Bij中的所有边仍能正常传输，没有流量损失，否则不能保持正常的传输。若所有的Dij值均大于0，说明全网N-1之后能够保持网络功能，若存在Dij小于0，说明在N-1条件下会有一部分流量损失，甚至导致网络崩溃。Dij反映了边流量安全或者不安全的程度，所以此模型不但可以用来判断工作点是否安全，还可以通过安全距离反映安全裕量，使网络在遭受打击的情况下不丢失或尽可能少丢失负载，从而提高网络的强健性。

为描述全网N-1安全程度，定义全网平均安全距离D和负的安全距离加权值DF分别为

(6)

(7)

其中，p为Dij值为负边的条数，N为边的总数。D反映了全网的平均安全裕量；DF是所有负的安全距离的加权平均，反映全网边的失效情况，当没有边失效时DF为0。

综上，式(4)描述安全域边界，式(5)描述边的安全裕量，式(6)和(7)进一步对安全性进行整体评价。

3 实验分析

3.1 小规模通信网络

以一个五节点的小规模通信网[35]为例，其拓扑及容量配置如图2所示。其中边(通信网称链路)的流量值是计及所有节点之间的业务传递要求之后，业务量在边上的标量叠加[35]，本文中采用无量纲的表示形式。该通信网的负载重分配采用多径路由模型[29]，其迂回路由如表1。

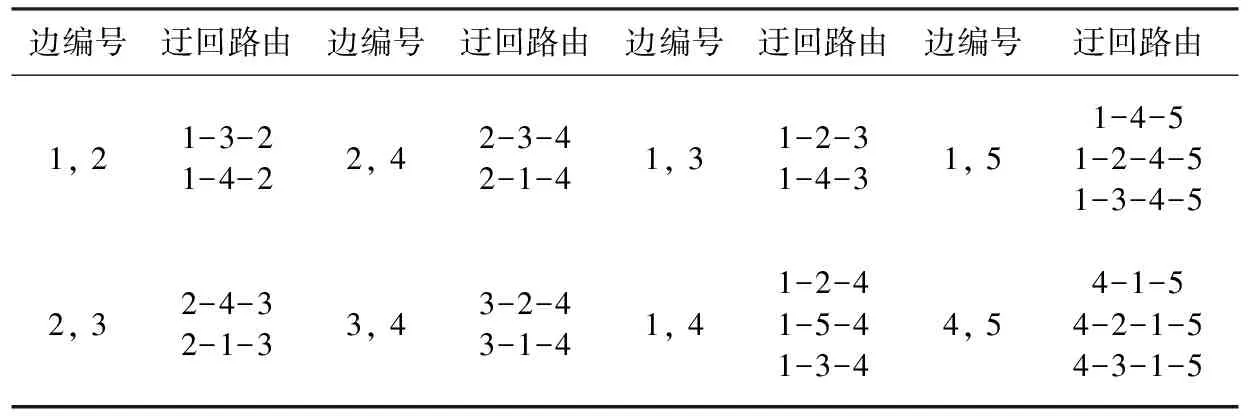
边编号迂回路由边编号迂回路由边编号迂回路由边编号迂回路由1，21-3-21-4-22，42-3-42-1-41，31-2-31-4-31，51-4-51-2-4-51-3-4-52，32-4-32-1-33，43-2-43-1-41，41-2-41-5-41-3-44，54-1-54-2-1-54-3-1-5

边失效后其负载在表1中的迂回路由上重分配，依据式(4)写出该算例的安全边界表达式(8)。式(4)中的Bij指表1中(vi,vj)边对应的迂回路由上边的集合，hmn为各迂回路由的权值所占比例，负载将按比例hmn分配，权值取迂回路由容量，等于路由中最小边的容量。

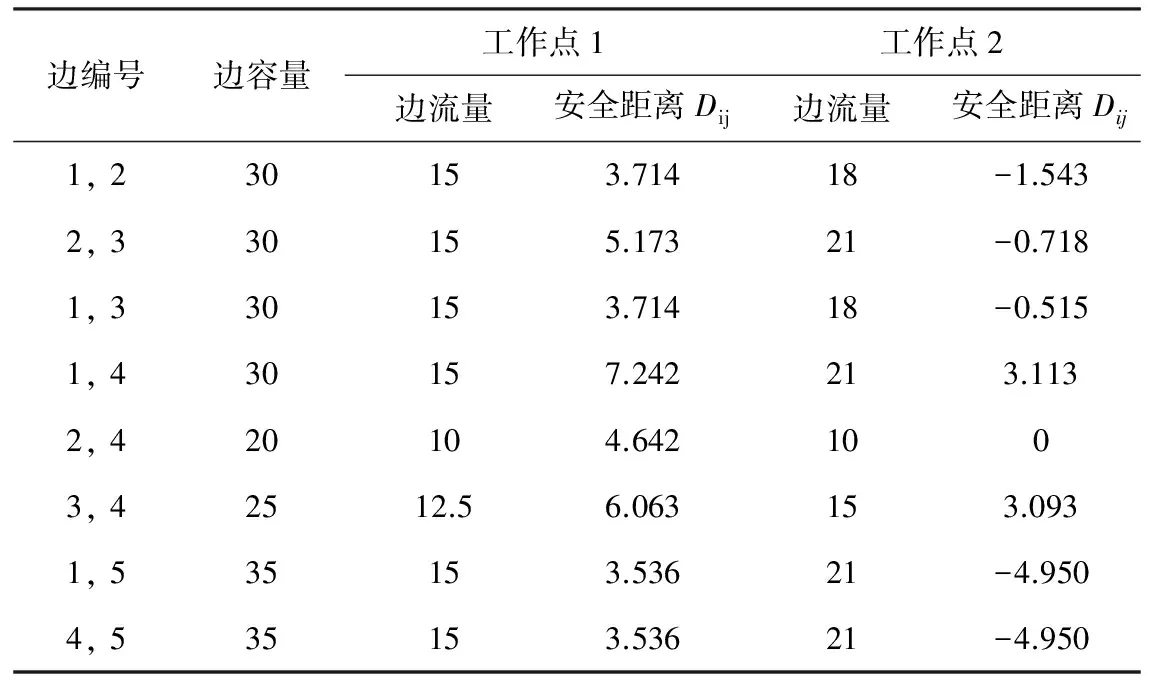
(8)

式(8)表示的是每条边流量、容量与其他边的关系，其所决定的超平面围成的区域就是这个网路的安全域。分别取两个工作点：工作点1流量和为112.5，工作点2流量和为145，每个边的流量及根据式(5)计算出的边的安全距离Dij见表2。

从表2看出，工作点1的安全距离Dij都大于0，经计算平均安全距离D为4.702，负的安全距离加权值DF为0，所以该工作点是N-1安全的。为证实该结论，对所有边逐条做N-1仿真，校验结果表明都能满足安全约束。工作点2有5个Dij为负值，D为-0.809，DF为-2.535，因此是N-1不安全的。这5个Dij为负边发生N-1时均引起失效。可见，Dij体现了网络在N-1后的安全或不安全的程度，D体现了全网的安全水平，DF的值反映N-1不安全的边的情况。

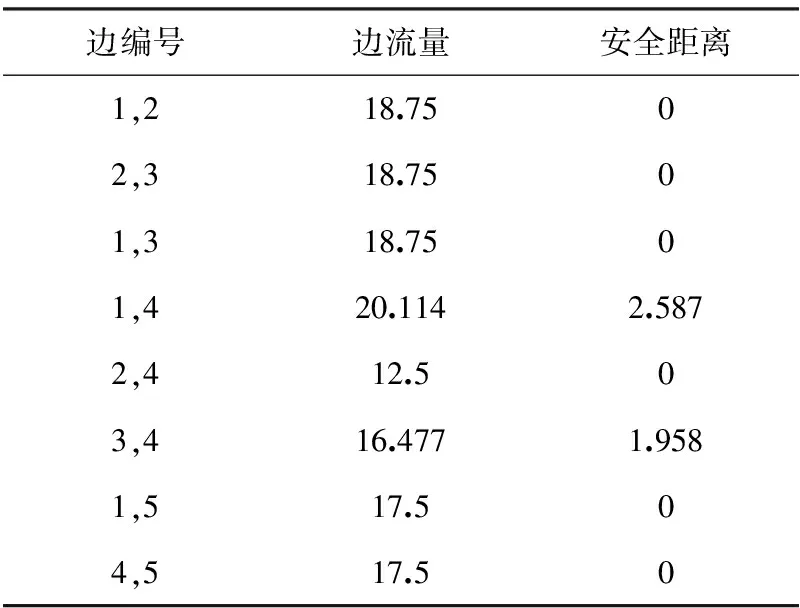
表3 临界安全的工作点3的安全距离

工作点3是临界通过N-1安全约束的点，总流量140.341，各条边流量及安全距离见表3。

观察工作点3看出，有6条边的安全距离Dij均为0，其它几条边Dij虽然大于0，但这些边流量的稍微增加就会引起其他边的N-1不安全，所以工作点3是临界安全的工作点。

对于不安全的工作点，还能够利用安全域方法进行调整，使之变为安全的工作点。观察工作点2的超平面情况可知，为负的安全距离Dij是由f23、f45和f15的负载重分配引起的，以式(8)为约束条件，f23、f45和f15减少量之和最小为目标函数，得到调整策略为：f23减小1.8，f45和f15均减小3.5，流量调整为17.5，经计算，调整之后工作点安全距离全部变为非负值。对安全域可视化可更形象显示调整前后的变化。以f45和f15为自变量，其它边流量保持工作点2值不变，可以得到图3中f15、f45的二维关系图。

图3中工作点只要在灰色边界内部变化，网络都是N-1安全的；灰色边界是临界安全工作点集合，即为安全边界；边界外部是不安全点的集合。可以看出，根据安全域所设计的调整措施将边界外不安全运行的工作点拉回到域内，提高了系统的安全性水平，能够通过预防性的负载调整防止N-1不安全现象的发生。

3.2 较大规模一般网络

采用Pajek工具[4]生成的有着M= 500 个节点和N= 1 000 条边的较大规模随机网络, 边的流量fij=(kikj)θ,fij=αijCij,αij为边的负载率,Cij为边的容量, 负载重分配策略为最近邻重分配策略[12], 通过软件计算将本文方法应用于此人工网络。安全运行边界可表示为(此网络边和节点较多, 简化表示安全运行边界如下： 其中，fi,i=1,2，…，N表示流量ci,i=1,2，…，N表示容量。3.3中也按此种方法表示)

(9)

式(9)中完整的不等式约束共1 000个, 每条边的约束不等式个数依据相连边的个数而定。安全域由不等式对应的超平面所确定。给定工作点后, 通过式(5)、(9)得到各条边的安全距离。以边f976和f828以及f827为例,将其他边的流量值固定在临界安全工作点上, 分别作安全域可视化的二维图和三维图如图4所示。

3.3 大规模电力网络

以有M= 4 941 个节点和N= 6 594 条边的美国西部电网为例。边的流量fij=(kikj)θ，fij=αijcij，αij为边的负载率，cij为边的容量，负载重分配策略是最近邻重分配策略[12]，每条边的不等式约束个数依据重分配时近邻边的个数而定，Bij是与失效边近邻边的集合，分配比例hmn由近邻各边权值所占比重得到[12]。例如f1失效后近邻边有两条，所以约束有2个，分配比例分别是0.143和0.857。通过软件计算将本文方法应用于此网络，安全域的边界表达式为(此网络边和节点较多，简化表示安全边界如下：其中fi，i=1,2，…，N表示流量；ci，i=1,2，…，N表示容量。)

(10)

式(10)中不等式约束共6 594组，给定工作点后，通过式(5)、(10)可以得到各条边的安全距离以及全网的D和DF值。同样可以通过程序得到边的二维图或三维图，以此实现安全域中工作点的可视化。以边f1和f2以及f3为例，将其它边的流量值固定在临界安全的工作点上，得到安全域可视化如图5所示。

4 与抗毁性的对比验证

给定一个工作点，既可以计算其抗毁性，也可以计算工作点到安全边界的距离，这两个数据都反映了网络对抗元件失效的能力。将二者对比，以校验安全域方法的正确性并归纳其特点。抗毁性计算采用基于最近邻重分配准则的级联失效抗毁性计算方法[12]。计算公式为

Rij=Nij/N

(11)

(12)

其中，Rij为边(vi，vj)的抗毁性值，R为全网每条边Rij平均值，本文用失效后网络的最大连通片尺寸与网络尺寸之比来度量网络的抗毁性。N表示N-1前网络中边的数目，Nij表示N-1后边(vi,vj)最大连通尺寸中边的数目。

4.1 对比验证步骤

设计对比验证方案，并编制程序，步骤如图6所示。

由图6主程序可得到多个工作点下的安全距离D、DF和抗毁性R。g为工作点的组数；安全距离计算子程序得到工作点到各边的安全距离；抗毁性计算子程序得到单条边失效的抗毁性值Rij。在5.2的各组验证中只需根据需求改变主程序中边的流量的初值即得到各组数据，用Matlab画出相应的对比图像见图7、图8和图9。

4.2 对比验证结果

4.2.1 不同负载水平下的对比

在西部电网算例中，取全网各条边的αi值相同均为α，α从0.5取到1，得到21组流量的初值，根据图6的步骤，对比一系列流量分布相同负载水平不同的工作点的抗毁性值和安全距离值，结果如图7所示(θ=1)。

从图7可看出，随着边的负载率α的增加，负安全距离加权值DF在α值为0.68附近时开始从0下降，说明有N-1不安全边的出现，此时抗毁性R也开始明显下降，DF和R相一致，这些现象符合目前研究网络呈现的特性[12,36]，即随着整体流量强度的增加网络承受打击的能力呈规律性减弱。平均安全距离D呈下降趋势，也能够很好反映负载水平逐渐增长过程中网络安全性的逐步降低。不同的是平均安全距离D能给出安全或不安全的裕量值，各工作点的D值均不同，D能够更好地区分各个工作点的差异。各个工作点的Di值还可以更具体地反映各边的N-1安全程度。

4.2.2 总流量固定不同分布下的对比

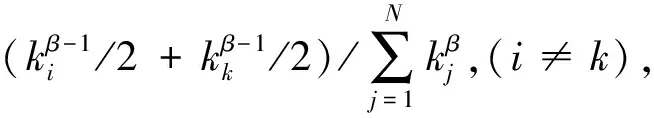
从图8中可以看出，随着β值的调整即全网流量分布的变化，安全距离和抗毁性的变化是完全一致的。当β值在-2到3之间时，网络的安全性能最好，R值为1，Di没有负值出现，DF为0。β值向两侧变化时网络的安全性降低，β正向变化时R、D和DF出现突然性的下降，β负向变化时三者降低比较缓慢，但趋势都是相同的。可见，β为负值时，网络的安全可靠性较好[36]，故可以在整体流量不丢失的情况下调整β，优化分布，得到安全距离和抗毁性值大的较安全的工作点。

4.2.3 逐步增加流量时的对比

从图9看出，当流量从临界安全点开始逐步增大时，R、D、DF均呈相同的下降趋势，表现为越来越不安全；当边的流量值从临界安全点减小时，网络是N-1安全的，R和DF的值分别保持1和0不变，平均安全距离D呈逐步上升，更好地区分了各工作点。

以上三项对比在4.1的算例中也得到了相同的结论。综上，安全距离和抗毁性在网络可靠性评价上具有很高的一致性，DF和R的趋势相同，平均安全距离D值能更好区分工作点安全时的裕量。

4.3 计算速度与时间复杂度对比

在4.2.1中的对比中，取20个工作点，对于M= 4 941和N= 6 594的大规模电网，安全距离计算时间是23.77s，抗毁性计算时间是99 132.12s，两者比值是1/4 170；对M=500和N= 1 000的ER人工网络，安全距离计算时间是5.18s，抗毁性计算时间是4 672.14s，两者的比值是1/902。

为证明普遍性，对两者的时间复杂度进行比较。需要指出的是，安全距离的计算过程中并不需要进行重分配，但是重分配所决定的超平面个数会影响到安全距离的计算的复杂度。例如基于最近邻原则，重分配后根据式(5)需要对近邻的每条边的安全距离进行计算，每条边涉及到的超平面个数由相邻节点的度决定。设计算全网安全距离D的时间复杂度为T1(N)，节点i的度为ki，则

(13)

对于均匀的NW网络，有全网节点度的平均值〈k〉=2N/M，〈k〉/〈k2〉≈1/〈k〉[12],所以有：

T1(N)=M〈k2〉-2N≈M〈k〉2-2N=4N2/M-2N<4N2/M=o(N2/M)

(14)

而对于非均匀网络，如BA网络，〈k2〉=m2ln(M),(m≤m0)[12]，m0是网络生长的初始规模[37]，是一个不大的常数，所以有：

(15)

而对于抗毁性，由式(11)、(12)和4.1中计算R值的步骤可知，无论对哪种网络，每计算一条边的Rij值，都要经过r((1

安全域方法更快，这是由于对于给定网络，安全边界可预先计算得到，只要网络不变对不同工作点可反复使用，安全分析时只需要计算工作点到边界距离。安全距离计算不需迭代。而每一条边的抗毁性计算都需要1至N步级联迭代得到，计算的步数r在1和N之间，所以特别是网络的规模变大时，时间复杂度呈平方增长，其计算会远慢于安全距离的计算。综上，安全距离计算速度远快于抗毁性，更适合在线安全分析。

5 结论

本文提出了适用于一般网络的安全域概念，并给出N-1安全边界的解析算法，定义的安全距离可以对网络的安全性、强健性做出评估。在不同规模和类型网络中验证了本文方法的有效性，与抗毁性方法结果有很高的一致性。

本文方法为网络遭受外部攻击或内部失效后的安全性分析和预防措施研究提供了新方法，具有如下特点：1)可不经仿真，未知流量负载仅根据拓扑及容量配置给出安全运行的区域；2)对工作点可以很好区分，通过距离边界的安全距离给出安全或者不安全的程度；3)域边界可预先离线计算，能快速判断工作点安全性，时间复杂度明显低于抗毁性计算，更适合在线安全分析；4)安全距离还指示了控制措施的方向和强度，是安全控制的基础。

需要指出，安全域不是抗毁性方法的替代，而是从另一种角度对网络的健壮性与运行可靠性进行了描述。此外，本文仅给出N-1的解析方法，对于同时多个元件失效的N-X，其发生概率相对很小，尚未涉及，在后续研究可以在N-1基础上扩展。

[1]Wen H, Lin C, Ren F, et al. Retransmission or redundancy: transmission reliability in wireless sensor networks[J]. Sci China Ser F, 2012, 55(4): 737-746.

[2]Chen Y Z, Li N, He D R. A study on some urban bus transport networks[J]. Physica A: Statistical Mechanics and its Applications, 2007, 376(1): 747-754.

[3]Min Y, Jin X, Chen M, et al. Pathway knockout and redundancy in metabolic networks[J]. J Theor Biol, 2011, 270(1): 63-69.

[4]Albert R, Jeong H, Barabási A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378-382.

[5]谭跃进, 吕欣, 吴俊, 等. 复杂网络抗毁性研究若干问题的思考[J]. 系统工程理论与实践, 2008(增刊): 116-120. Tan Yuejin, Lu Xin, Wu Jun, et al. On the invulnerability research of complex networks[J]. System Engineering Theory & Practice, 2008( Suppl): 116-120.

[6]Borgatti S P, Mehra A, Brass D, et al. Network analysis in the social sciences[J]. Science, 2009, 323(5916): 892-895.

[7]Cohen R, Erez K, Ben-Avraham D, et al. Breakdown of the Internet under intentional attack[J]. Phys Rev Lett, 2001, 86(16): 3682.

[8]Liu H R, Dong M R, Yin R R, et al. Cascading failure in the wireless sensor scale-free networks[J]. Chin Phys B， 2015, 24(5): 050506.

[9]Ouyang M. Comparisons of purely topological model, betweenness based model and direct current power flow model to analyze power grid vulnerability[J]. Chaos, 2013, 23(23):023114.

[10] Bashan A, Berezin Y, Buldyrev S V, et al. The extreme vulnerability of interdependent spatially embedded networks[J]. Nature Physics, 2013, 9(10): 667-672.

[11] Buldyrev S V, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028.

[12] Wang W X, Chen G R. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E, 2008, 77(2): 20-28.

[13] 段立东, 武小悦. 基于可调负载重分配的无标度网络连锁效应分析[J]. 物理学报, 2014, 63(3): 030501. Duan LiDong, Wu Xiaoyue. Cascading failure of scale-free networks based on a tunable load redistribution model[J]. Acta Phys Sin, 2014, 63(3): 030501.

[14] 戴存礼, 吴威, 赵艳艳, 等. 权重分布对加权局域世界网络动力学同步的影响[J]. 物理学报, 2013, 62(10): 108903. Dai Cunli, Wu Wei, Zhao Yanyan, et al. Effect of weight distribution on the synchronization of weighted generalized local-world networks [J]. Acta Phys Sin, 2013, 62(10): 108903.

[15] 张喜平, 李永树, 刘刚, 等. 节点重要度贡献的复杂网络借点重要度评估方法[J]. 复杂系统与复杂性科学, 2014, 11(3): 26-32. Zhang Xiping, Li Yongshu, Liu Gang,et al. evaluation method of importance for nodes in complex networks based on importance contribution[J]. Complex Systems and Complex Science, 2014, 11(3): 26-32.

[16] Wang L W. Origin of the stronger robustness against cascading failure of complex networks: a mitigation strategy perspective[J]. Mod Phys Lett, 2013, 27(3): 1350023.

[17] Lakervi E, Holmes E J, et al. Electricity distribution network design [J].Lee Review， 1990, 36(4):340.

[18] Hnyilicza E, Lee S T Y, Schweppe F C. Steady-state security regions: the set-theoretic approach [J]. Proceedings of the PICA Conference, 1975:347-355.

[19] Ding T, Guo Q L, Bo R, et al. A static voltage security region for centralized wind power integratio —part I concept and method [J]. Energies, 2014, 7(1): 420-443.

[20] 余贻鑫. 电力系统安全域方法研究述评[J]. 天津大学学报, 2008, 41(6): 635-646. Yu Yixing. Review of study on methodology of security regions of power system[J]. J Tianjin Univ,2008, 41(6): 635-646.

[21] Liu F, Wei W, Mei S W. On expansion of estimated stability region: theory, methodology, and application to power systems[J]. Sci China Ser E, 2011, 54(6): 1394-1406.

[22] Liu Y L, Yu Y Y. Probabilistic steady-state and dynamic security assessment of power transmission system[J]. Sci China Ser E, 2013, 56(5): 1198-1207.

[23] 秦勇, 史婧轩, 张媛,等. 基于安全域估计的轨道车辆服役状态安全评估方法[J]. 中南大学学报(自然科学版), 2013(s1):195-200. Qin Yong, Shi Jingxuan, Zhang Yuan, et al. Research on method framework of security region estimation in rail transit system operation safety assessment[J]. J Central South Univ (Sci Technol), 2013(s1):195-200.

[24] Goldsmith A. Capacity limits of MIMO channels [J]. IEEE Journal on Selected Areas in Communications, 2003, 21(5): 684-704.

[25] 余贻鑫, 栾文鹏. 智能电网述评[J]. 中国电机工程学报, 2009(34), 29: 1-8. Yu Yixin, Luan WenPeng. Smart grid and its implementations[J]. Proceedings of CSEE, 2009, 29(34): 1-8.

[26] 肖峻, 贡晓旭, 王成山. 智能配电网N-1安全边界拓扑性质及边界算法[J]. 中国电机工程学报, 2014, 34(4): 545-554. Xiao Jun, Gong XiaoXu, Wang ChengShan. Topological properties ofN-1 security boundary for smart distribution network[J]. Proceedings of CSEE, 2014, 34(4): 545-554.

[27] Xiao J, Gu W Z, Wang C S. Distribution system security region: definition, model and security assessment[J]. IET Generation, Transmission & Distribution, 2012, 6(10): 1029-35.

[28] 肖峻, 贺琪博, 苏步芸. 基于安全域的智能配电网安全高效运行模式[J]. 电力系统自动化, 2014,38(19): 52-60. Xiao Jun, He Qibo, Su Buyun. A secure and efficient operation mode for smart distribution networks based on security region[J]. Automation of Electric Power Systems, 2014, 38(19): 52-60.

[29] Felemban E, Chang-Gun L, Ekici E. Multipath routing techniques in wireless sensor networks: a survey[J]. Wireless Pers Commun, 2013, 70(2): 807-829.

[30] 张景中. 数学辞海第五卷[M]. 北京: 中国科学技术出版社, 2002:10-11.

[31] 黄汉江. 建筑经济大辞典[M]. 上海: 上海社会科学出版社, 1990：230.

[32] Halpi N S M, Harley K A. Anticipatory load shedding for line overload alleviation using teaching learning based optimization[J]. IEEE Electrical Power and Energy Systems, 2014, 63(12): 862-877.

[33] Zhang A M H, Gao Z Y, Ren H L. Incident-based traffic congestion control strategy[J]. Sci China Ser E, 2011, 54(5): 1338-1344.

[34] Graham C, Robert P. Self-adaptive congestion control for multiclass intermittent connections in a communication network[J]. Queueing Syst, 2011, 69(3-4): 237-257.

[35] 陈建国. 网络分析与设计的抗毁性量度剖析[J]. 无线电工程, 1998(6), 28: 12-17. Chen Jianguo. Study on measure of invulnerability for network design and analyst[J]. Radio Engineering, 1998, 28(6): 12-17.

[36] 李勇, 邓宏钟. 不同流量的复杂保障网络抗毁性仿真分析[J]. 火力与指挥控制, 2010, 35(3): 9-13. Li Yong, Deng Hongzhong. Simulated analysis of complex networks with different flows[J]. Fire control & command control, 2010, 35(3): 9-13.

(责任编辑 耿金花)

Secure Region of Network and Comparison with Invulnerability

XIAO Jun1，SU Buyun2，LI Xin3，WANG Chengshan1

(1.Key Laboratory of Smart Grid of Ministry of Education, Tianjin University,Tianjin 300072，China2.Guangdong Electric Power Design Institute, CEEC, Gungzhou 510663，China；3.Sichuan Electric Power Research Institute, Chengdu 610072， China)

This paper presents a new method for security analysis and precautionary measures when attack or error occurs in networks. This method describes the operating region underN-1 constraint and presents the degree of security or insecurity by secure distance to indicate direction and intensity for next step. We put the method into effect in general networks, small communication network and large-scale power network to verify its correctness, and compare it with network invulnerability. It can be seen that secure distance index and invulnerability index are very consistent in judging the reliability of a system, meanwhile, the former can bring secure region information to eliminate hidden dangers in advance and be appropriate for online security surveillance and control based on faster calculation speed.

secure region；N-1 boundary； secure distance； network invulnerability

10.13306/j.1672-3813.2016.04.006

2015-06-28；

2015-10-09

国家自然科学基金(61273152,61304052,51407088)；山东省自然科学基金(BS2015DX018)

肖峻(1971-)，男，四川成都人，博士，教授，主要研究方向为配电网规划及安全可靠性研究。

N94

A