产生幂律等分布的一种机制

李鹤龄,王娟娟,杨 斌，2,沈宏君，2(.宁夏大学物理电气信息学院，银川 75002；2.宁夏沙漠信息智能感知重点实验室, 银川 75002)

产生幂律等分布的一种机制

李鹤龄1，2,王娟娟1,杨 斌1，2,沈宏君1，2
(1.宁夏大学物理电气信息学院，银川 750021；2.宁夏沙漠信息智能感知重点实验室, 银川 750021)

针对在复杂性系统研究中幂律分布扮演着越来越重要的角色而又不存在公认的合理导出的矛盾，基于复杂性系统的不可解性，在非完整统计的思想基础上，分别在归一化条件、统计平均和Shannon熵的方程中引入不同的指数因子，由最大熵原理推导出了指数函数、幂函数和幂函数与指数函数乘积形式的概率分布函数；展现了由Shannon熵和最大熵原理推导等概率假设的过程；同时也展现了可导出指数分布、幂律分布和幂函数与指数函数乘积形式分布的一种新机制，即最大熵原理。

复杂系统；非完整统计；Shannon熵；幂律分布

0 引言

由统计物理研究事物的性质与运动规律时，要确定所研究系统的概率分布函数，即统计分布函数。基于等概率原理(常称等概率假设)由统计物理的系综方法可导出统计分布的指数函数形式[1],如：正则分布、巨正则分布等；基于Shannon熵由最大熵原理不仅能导出概率分布的指数函数形式[2]，而且可导出等概率假设，因而最大熵原理可看成是基于指数分布的统计物理的基本出发点或基本假设。指数分布使得统计物理获得极大的成功已成为不争的事实，但近些年来，不仅物理学领域几乎每一种科研领域都遇到了幂律分布[3]，且以井喷之势发展。有关幂律分布的形成机制存在多种不同观点：增长与优先连接[4-5]、自组织临界[6-7]、HOT理论[8-9]、渗流模型[10-13]、随机过程[10,14-15]、指数组合[10,14,16]等。遵循幂函数与指数函数乘积形式的概率分布也很常见[17-18]，但遗憾的是直至目前仍然没有由Shannon熵导出幂律等分布的合理逻辑推导，而且指数、幂律等其它多种不同分布之间是否有联系等等疑问也尚无确定结论。本文尝试由Shannon熵及最大熵原理推导出指数和幂律等不同分布，以图揭示不同事物间的内在联系及形成指数、幂律和幂和指数函数乘积等不同形式分布的一种原因。

巴西物理学家Tsallis于1988年给出了非广延的Tsallis熵[19]；并基于Tsallis熵和最大熵原理，推导出了Tsallis形式的幂律分布[19-20]。Tsallis理论的闪光点在于将指数分布的统计物理带到了幂律分布，但该理论目前并未被科学界普遍接受。对Tsallis熵、Tsallis统计，从其提出开始，就一直存在激烈的争论。因而由普遍认可的Shannon熵推导出幂律分布就显得迫切和意义重大。

注意到Tsallis熵包含Shannon熵，即当Tsallis熵中的非广延参数趋于1时，Tsallis熵趋于Shannon熵。虽然由Tsallis熵能够推导出Tsallis形式的幂律分布，但按此逻辑关系，并不意味着由Shannon熵也能推导出幂律分布！因为Tsallis熵中的非广延参数趋于1的同时，Tsallis形式的幂律分布也趋于指数分布。因此必须设法由Shannon熵直接推导幂律等分布。

1 由Tsallis熵推出Tsallis型的幂律分布及Tsallis统计质疑的简单回顾

Tsallis熵为：

(1)

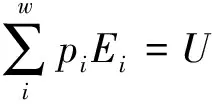
(2)

(3)

(4)

在q→1时，Tsallis熵趋于Shannon熵,Tsallis型的幂律分布趋于指数分布。

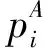
Sq(A∪B)=Sq(A)+Sq(B)+(1-q)Sq(A)Sq(B)/k

(5)

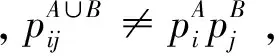
Tsallis统计在第1种约束下会出现不稳定、发散和不相容问题[20]；在第2种约束下会出现能量不守恒问题，如无相互作用子系统A与B 的“并系统”内能不等于它们的和[21-22]：

(6)

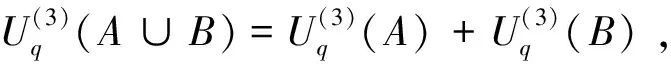
这样，虽然由 Tsallis熵可推导出幂律分布，但因Tsallis熵自身存在的以及其能导致能量不守恒等问题，使人们对Tsallis统计存有质疑。到目前为止，Tsallis理论并未被科学界所普遍接受。

2 “非完整”统计简述

(7)

这样，变量O的统计平均值可设为

(8)

以式(8)为基础的统计物理称为非完整统计。

Shannon熵为

(9)

式中的k为玻尔兹曼常数，式(9)也可写成

因此在非完整统计下的Shannon熵为[23-24]：

(10)

显然，当q=1时，式(10)过渡为通常的Shannon熵。

3 基于Shannon熵和最大熵原理的指数分布和等概率假设的推导

3.1 基于 Shannon熵和最大熵原理的指数分布

最大熵原理是Jaynes E.T.在1957年首先提出的[2]，可简述为：系统在一定外界环境或约束下所处的状态(或概率分布)，是系统处于该环境或约束条件下熵取最大值的状态(或概率分布)。

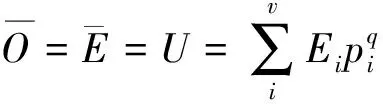
(11)

式(11)中的β和γ为Lagrangian乘子。根据最大熵原理，令L/pi= 0，得：

(12)

式中

(13)

这样得到了指数函数形式的统计分布。令q=1，就得到通常情况下的正则分布与正则配分函数。上述为Q.A.Wang所做工作[23-24]。

3.2 由Shannon熵和最大熵原理推导等概率假设[25]

等概率假设为：孤立系统的每个微观态的概率相同。对于孤立系统，粒子数、能量和体积都不变，此时只有归一化条件的限制。由最大熵原理，取Lagrange函数为(取完整统计):

(14)

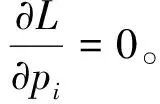
pi=e-1-γ

(15)

pi=e-1-γ=1/w

(16)

式(16)正是孤立系统的等概率假设。

4 基于Shannon熵和最大熵原理的幂律等分布

注意到复杂系统的不可解性，势必会出现信息的不完整，即：v≠w。由非完整统计的思想，且注意到式(7)、式(8)和式(10)是不同的和式，从数学角度，当选择了适当的q使式(1)成立时，同一个q不一定能使(8)和式(10)同时成立，因而3式中的q并不要求一定相等(非完整统计的引入者Q.A.Wang取3个q相等[23-24])，这里分别表示为a,b,c。当a=b=c=1时，对应于简单的v=w可解系统，概率分布为式(12)，(13)中q=1的指数函数分布；a,b,c越偏离1,说明系统的不可解性、复杂性程度越高，即非1的a,b,c反映了系统的不可解性和复杂性。此时式(7)、(8)和(10)如式(17)所示：

(17)

式(17)中Ei并不受限于能量，它可以是任意描述复杂系统性质的具有平均值的量。引入Lagrangian 函数

(18)

同样β和γ为Lagrangian乘子。求条件极值，得

(19)

显然，当式(19)中的a，b，c相等时，得指数分布函数式(12)；不等时，既解不出指数函数也解不出幂函数形式的分布函数。

为得到pi为Ei的显函数形式，又要与相关理论不矛盾，对参数a，b，c的取值作一些说明。

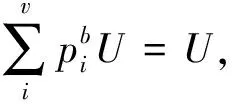
(20)

2) 在用于描述自然界与人类社会运动的各种变量中，除了像能量这类守恒量外，还有一些如“能力”以及与能力对应的“产量”等非守恒量,它们并不简单地满足如“1+1=2”的线性叠加关系，对于这类“非守恒变量”，不需要a=b的限制。

式(19),(20)中的a,b,c和γ与Ei，pi无关，为简单起见。令y=pi，x=βEi，则式(19),(20)变为

(19′)

(20′)

要从(19′)或(20′)解析地解出y(x)的显函数是做不到的。但根据前述3个参数相等时所得指数函数的显函数及这两式中存在变量y的幂函数、幂函数与对数函数乘积的特点，有理由认为y(x)的具体函数形式应在指数函数、幂函数和幂函数与指数函数乘积之间。考虑到实际得出幂律分布源于直接或间接实验或实测数据的逻辑推演，而实验或实测数据只能在有限时空中完成，即数据数量有限，本文采取对概率分布函数的自变量“分段”的数值求解方法。理由阐述如下：

1) 数值求解不仅是(19′)、(20′)无法解析求解的必然选择，也是实际复杂系统获取幂律等分布的途径。

3) 当所有可能事件个数为测度不为零的无穷大时，按pi=Ni/N获得的概率分布应是以最概然值为中心的有限半径范围内的一段分布。在统计物理中最典型的例子是：因平衡态对应的微观状态数占绝对多数，以至于最概然值等于平均值。仅以位置分布为例。等概率假设虽然认为所有粒子集中在某一边缘位置的概率与均匀分布中的一个任意状态的概率相等，但实验测得的结果一定是均匀分布，即最概然值。因为均匀分布对应的微观状态数是绝对多数。具体复杂性系统得出幂律分布的结论也是由直接或间接实验数据或实测数据的演绎结果，虽然一般不会像上述粒子位置分布这么极端，但有理由认为实验或实测数据描述的状态基本处于包含最概然值事件的邻域内。即便实验或实测中出现小概率事件，由于难于重复多次出现，也将被舍弃。对于不同具体问题只是“段”的位置和其长短的不同,即最概然值事件和其邻域半径的不同。

具体数值求解步骤为：

1) 将a,b,c和γ(γ都取10，对应未归一化的概率分布)取值并代入式(19′)、(20′)，由计算机做出y-x曲线图。

2) 调换x与y，即调换横纵坐标，得到x-y曲线图。

3) 在纵坐标y从1到6的变化范围内均匀地在曲线上取60个点，做“整体”拟合后，优选最佳函数。

4) 将60个点分为6段(每10个点为一段，称“短段”)，分段拟合后，优选最佳函数。

a,b,c分别取8种不同数值, 优选拟合出y-x关系，如表1所示。

表1 a,b,c分别取8种不同数值时整体拟合的优选函数及误差Tab.1 Optimal fit functions and errors for eight different value of a,b and c

再将每组数据的60个点平均细分为6段，每段仍用不同的函数拟合并优选出最佳结果，如表2至表9所示，前述几种函数也都有出现，且还会出现Tsallis形式的幂函数、负指数函数与负幂函数乘积、正指数函数与负幂函数乘积等形式，且拟合误差都小于10-4。

表2 a=b=0.96,c=0.98，分段(每段10个点)拟合结果Tab.2 Piece-wise fitting (a=b=0.96,c=0.98)

如表2所示，第1分段的最优拟合函数为Tsallis形式的幂函数y=1 623.778 49(1-0.028 53x)25.046 06；第2分段的最优拟合函数为负指数函数与幂函数的乘积y=251.541 2x2.570 53e-1.246 18x；第3段的最优拟合函数为负指数函数y=-0.101 29+3 171.412 9e-0.889 75x，当a，b,c取其它不同数值时的拟合结果可见表3至表9。

当a=b=0.97,c=1.02时，分段拟合结果如表3所示。

表3 a=b=0.97, c=1.02时，分段拟合结果Tab.3 Piece-wise fitting results (a=b=0.97,c=1.02)

当a=b=0.99,c=1.01时，分段拟合结果如表4所示。

表4 a=b=0.99, c=1.01时，分段拟合结果Tab.4 Piece-wise fitting results (a=b=0.99,c=1.01)

当a=b=1.50,c=2.04时，分段拟合结果如表5所示。

表5 a=b=1.50,c=2.04时，分段拟合结果Tab.5 Piece-wise fitting results (a=b=1.50,c=2.04)

当a=b=0.30,c=0.40时，分段拟合结果如表6所示。

表6 a=b=0.30,c=0.40时，分段拟合结果Tab.6 Piece-wise fitting results (a=b=0.30,c=0.40)

当a=0.90,b=1.15,c=1.25时，分段拟合结果如表7所示。

表7 a=0.90,b=1.15,c=1.25时，分段拟合结果Tab.7 Piece-wise fitting results (a=0.90,b=1.15,c=1.25)

当a=0.95,b=1.50,c=1.05时，分段拟合结果如表8所示。

表8 a=0.95,b=1.50,c=1.05时,分段拟合结果Tab.8 Piece-wise fitting results (a=0.95,b=1.50,c=1.05)

当a=1.25,b=0.98,c=0.95时，分段拟合结果如表9所示。

表9 a=1.25, b=0.98, c=0.95时，分段拟合结果Tab.9 Piece-wise fitting results (a=1.25,b=0.98,c=0.95)

5 结果与讨论

5.1 结果

针对复杂系统表现出遵循指数、幂律等分布，且幂律等分布不能像指数分布那样可由Shannon熵和最大熵原理导出的矛盾，我们做了如下工作：

1)展现了由Shannon熵和最大熵原理解析推导指数分布[式(6)，(7)]与等概率假设程。

2)注意到复杂系统的不可解性，以及反映复杂系统特征的随机变量的幂律等概率分布源于实验和实际测量，指出这样获得的概率分布实质是最概然值附近的一段，因而提出复杂系统的概率分布是按自变量分段的。

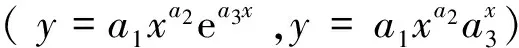
因为取a=b=c=1是获取传统指数函数形式“完整”正则分布的路径，所以本文中a、b和c的选取是以“1”为中心逐渐偏离的。又因幂律分布常出现于复杂性系统中，且本文并不涉及任何具体复杂性系统，所以理论上讲a，b，c越偏离“1”,系统的复杂性或非完整程度越高。

在具体推导过程中，我们发现：

1)每段的最优分布函数与指数因子a、b、c的具体数值有关，虽然a，b，c越偏离“1”, 系统的复杂性或非完整程度越高，但并不是每段的最优分布函数越背离指数函数。

2)在不同的区段或在自变量的不同变化范围内，最优分布函数会发生类型的转变，转变依指数因子a，b，c的具体数值有一定规律,但出现不同最优分布函数的具体形式不受限于a与b是否相等，也即出现幂律等分布与是否为守恒量无关。

3)分布函数的最优形式与分段的长短有关。如本文中的所谓“整体”相对于“分段”实质只是段长的不同，但选出的最优分布函数不同。这表明：复杂系统的概率分布函数会随自变量的取值区间不同而发生变化。这样的结果是与许多实际问题相吻合的。

4)当a=b=c=q时，分布函数可解析求出，为指数函数形式。

5.2 讨论

5.2.1 幂函数、幂函数与指数函数乘积等概率分布形式与Shannon熵

本文已展示可由Shannon熵和最大熵原理解析导出概率分布的指数函数形式，但对幂函数、幂函数与指数函数乘积形式，只能尝试用数值求解。

本文数值求解建立的基础是：复杂系统不可解性；复杂系统服从幂函数、幂函数与指数函数乘积形式的概率分布；幂函数、幂函数与指数函数乘积形式的概率分布是源于直接或间接的有限实验、实测数据得出。因而本文不涉及具体复杂系统的数值求解方法(也是普遍由具体复杂系统得出幂函数、幂函数与指数函数乘积形式的概率分布的方法)。故由基于Shannon熵和最大熵原理的数值求解方法得到幂函数、幂函数与指数函数乘积形式的概率分布可定性解释复杂系统出现这些概率分布形式的原因。

5.2.2 最大熵原理与等概率假设的关系

将Shannon熵和最大熵原理应用于孤立系统，可推导出等概率假设；反向推导也成立，即由等概率假设可推导出孤立系统的Shannon熵满足最大熵原理。但此结果仅限于孤立系统。虽然等概率假设在统计物理建立和发展过程中扮演了非常重要的角色，且目前仍是大多数统计物理教科书中得到概率分布的出发点,也是物理学家思想方法具体而闪光的体现,但同时它也被认为是人们无法确定微观态的概率的一种无奈的选择和假设。目前,用最大熵原理获取概率分布的文献也很多，如：Tsallis统计分布[19-20]、非完整统计分布[23-24]等。最大熵原理是比等概率假设更一般、包含内容更多、应用范围更广的基本原理。鉴于此，在统计物理中是否可用最大熵原理取代等概率假设以及等概率假设仅是最大熵原理的一个推论呢？这是可讨论的问题。

6 结论

指数分布以及复杂系统概率分布的幂函数、幂函数与指数函数乘积的形式可由基于Shannon熵的最大熵原理数值推导出来。也即说明最大熵原理是支配复杂系统运动的很重要的基本规律之一，不同形式的概率分布只是最大熵原理对不同形式复杂性系统的具体体现。

基于一些复杂性系统得出这几种概率分布是源于对有限直接或间接实验、实测数据按pi=Ni/N推理的结果，因而由基于Shannon熵的最大熵原理数值推导出来的幂函数、幂函数与指数函数乘积形式的概率分布，定性解释了出现这类概率分布的一种原因。

最大熵原理是比等概率原理包含内容更广的能反映自然与人类社会运动规律的基本原理，由其可推出等概率原理，因而等概率原理可看成是最大熵原理的一个推论。

[1]汪志诚.热力学·统计物理[M].第4版.北京：高等教育出版社, 2008.

[2]Jaynes E T. Information theory and statistical mechanics[J]. Phys Rev, 1957, 106(4)：620.

[3]胡海波，王林. 幂律分布研究简史[J]. 物理，2005，34(12)：989-996. Hu haibo,Wang Lin. A brief history of power law distributions [J]. Physics,2005,34(12):989-996.

[4]Albert R, Barabási A L. Emergence of scaling in random networks[J]. Science,1999,286:509.

[5]Barabási A L, Albert R. Mean-field theory for scale-free random networks[J]. Physica A,1999,272:173.

[6]Bak P, Tang C, Wiesenfeld K. Self-organised criticality:an explanation of 1/fnoise[J]. Phys Rev Lett,1987,59: 381.

[7]帕巴克.大自然如何工作[M].武汉:华中师范大学出版社, 2001.

[8]Carlson J M, Doyle J. Highly optimized tolerance: a mechanism for power laws in designed systems[J].Phys Rev E,1999,60:1412.

[9]Carlson J M, Doyle J. Highly optimized tolerance: robustness and design in complex systems[J].Phys Rev Lett,2000,84:2529.

[10] Newman M E J. Power laws, Pareto distributions and Zipf's law[J]. Contemporary Physics, 2004, 46(5):323-351.

[11] Broadbent S R, Hammersley J M. Percolation processes I crystals and mazes[J]. Proc Cambridge Philos Soc, 1957, 53:629.

[12] Hammersley J M. Percolation processes II the connective constant[J]. Proc Cambridge Philos Soc,1957, 53:642.

[13] Grimmett G. Percolation[M]. 2nd ed. Berlin: Springer-Verlag, 1999.

[14] Reed W J, Hughes B D. From gene families and genera to incomes and Internet file sizes: why power laws are so common in nature[J]. Phys Rev E, 2002, 66(6):067103.

[15] Mitzenmacher M. A brief history of generative models for power law and lognormal distributions[J]. Internet Mathematics, 2004, 1(2):226-251.

[16] Miller G A. Some effects of intermittent silence[J]. Amer J Psycho, 1957, 70:311-314.

[17] Fa K S. Continuous-time random walk: crossover from anomalous regime to normal regime[J]. Phys Rev E, 2010, 82(1)：012101.

[18] Boberski J, Shaebani M R, Wolf D E. Evolution of the force distributions in jammed packings of soft particles[J]. Phys Rev E, 2013, 88(6)：064201.

[19] Tsallis C. Possible generalization of Boltzmann-Gibbs statistics[J]. J Stat Phys, 1988, 52(1)：479-487.

[20] Tsallis C, Mendes R S, Plastino A R. The role of constraints within generalized nonextensive statistics[J]. Physica A, 1998, 261(3/4)：534-554.

[21] Li H L, XiongY, Li Y Y. The Tsallis statistical distribution in a completely open system[J]. Physica A, 2011, 390：2769-2775.

[22] 欧聪杰. 非广延统计物理中的四个基本问题与广义量子气体的热力学性质[D]. 厦门：厦门大学,2006. Ou Congjie. Four basic problems in nonextensive statistical physics and the ther modynamic properties of generalized quantum gases [D]. Xiamen: Xiamen Vniversity,2006.

[23] Wang Q A. Correlated electrons and generalized statistics[J]. Euro Phys J B, 2003, 31(1):75-79.

[24] Wang Q A. Extensive generalization of statistical mechanics based on incomplete information theory[J]. Entropy, 2000,5(2):220-232.

[25] 谭涛，李鹤龄. 统计力学基本假设的教学更新[J].大学物理，1997，16(1)：44-45. Tan Tao,Li Heling. Teaching renewal of basic hypothesis of statistical mechanics[J]. College Physics,1997,16(1):44-45.

(责任编辑 李进)

A Mechanism of Generating Power-Law and Other Distributions

LI Heling1,2,WANG Juanjuan1,YANG Bin1,2,SHEN Hongjun1,2

(1.School of Physics and Electrical Information Science, Ningxia University, Yinchuan 750021, China;2.Key Lab on Information Sensing and Intelligent Desert, Yinchuan 750021, China)

For resolving the contradiction between power-law distribution playing an increasingly important role in investigation of complex systems and it has not been derived out up to now, in this paper the maximal entropy principle and the idea of incomplete statistics were utilized. Firstly, the detail of deriving the equal probability hypothesis from Shannon entropy and maximum entropy principle was showed. Then three different exponential factors were introduced in equations about the normalization condition, statistical average and Shannon entropy respectively. Based on the Shannon entropy and maximum entropy principle, three different probability distribution functions, such as exponential function, power function and the product form consisting of power function and exponential function, were derived out. Which demonstrated the maximum entropy principle was a path which may lead to different distribution functions.

complex systems； incomplete statistics； Shannon entropy； power-law distribution

10.13306/j.1672-3813.2016.04.003

2015-01-20；

2015-11-16

国家自然科学基金(61167002) ；宁夏自然科学基金(NZ14055)

李鹤龄(1960-)，男，河北沧州人，硕士，教授，主要研究方向为复杂系统和反常统计物理。

杨斌(1974-)，男，山西运城人，硕士，副教授，主要研究复杂系统和理论物理。

N94

A