借题启智意在生智

江斌杰

[摘 要] 在笔纸化考评机制的大背景下，试卷是教师教学、学生学习的一种主要教学工具，工具的使用效果和效率都是我们需要不断优化和完善的，只有这样，我们才能真正提升试卷的价值，服务于学生的应试，更服务于学生能力的提升. 笔者结合试卷讲评这一环节，就如何优化试卷价值，提升讲评效果进行策略分享，欲以此抛砖引玉.

[关键词] 试卷；讲评；借题；课堂；智慧

俗话说“温故知新”，就是为了巩固学过的东西. 而为了了解学生对学过知识的掌握情况，便出现了各种检测试卷. 作为数学教师的笔者深知让学生从试卷中发现问题并分析错因，培养学生对试卷部分试题的解题方法、思想的归纳、提炼，让学生学会分享自己对部分试题的创新思维的重要性，所以试卷讲评的高效不仅可以让学生跳出“题海”，也切实提高了教学质量，同时也符合当下素质教育改革的形势. 下面，笔者就从如何引导学生主动参与数学试卷的讲评，以课堂为主阵地“借题释放”，以学生的试题为载体“借题发挥”等方面谈谈自己的一些做法，以供同行们参考.

以课堂为阵地“借题释放”

1. 尊重学生自尊，创设讲评氛围

学生是讲评的主体，教师是讲评的组织者、引导者、参与者，所以教师要“尊重学生的自尊心”，培养学生在试卷讲评课中积极向上的心理，以促进学生进步的内驱力，这是师生互动交流的基础. 著名的“皮格马利翁效应”告诉我们：说你行，不行也行；说你不行，你就不行，行也不行. 因为人的大脑是一个动态的“创造物”，只要善于开发就能启动“心理原子弹”的按钮，使得智慧迸发出绚丽的光彩，因此，教师在讲评前要尽量寻找、收集、捕捉学生试卷中的闪光点、创新点，作为讲评的情感资源，讲评时以不同的形式充分让学生展示独特的思维、思维的断点，并给以合适、积极的评价方式使得学生获取成功的喜悦、分享的快乐，从而促使每一位学生积极主动地参与讲评，让他们健康、快乐地成长.

2. 营造民主氛围，建立讲评信心

面向全体，以学生为主体的讲评告诉我们，必须营造民主的讲评氛围，从“教师讲，学生听”的单向信息传递转变为“教师与学生，学生与学生，学生与教师”的多渠道、多层面、全方位的信息传输和反馈，所以我们要鼓励学生敢于提问、善于提问、不动就问，并且将问题放到学习小组甚至全班进行合作交流，让学生从自己的“最近发展区”出发，在民主的学习氛围中获取成功的体验，并建立较强的自信心.

3. 引导学生互动，提升讲评能力

在每一次的答题中，学生的个性差异是客观存在的，所以教师要善于发现学生个性的答题、个性的讲评，在学生充分暴露思维的断点时作适时的点拨、引导；在参与小组、全班的交流时逐步让学生形成“兵教兵、兵帮兵”的学习方式，并养成学生勇于展示、乐于分享的良好的讲评习惯；优秀的学生在小组合作、全班交流的展示时，教师应给予肯定和鼓励，并关注学生题后反思学习习惯的养成，从而让学生在师生互动、生生互动中提升讲评能力.

4. 适时精讲细评，关注讲评细节

针对共性讲评资源，进行全班交流讨论时，教师得适时精讲细评. “适时”，即在学生想明白而不明白时、学生想说而又不能确切地说出时、学生的表述不够全面之时、学生的思维单一之时，此时就需要教师的耐心引导、入情入理的仔细的讲评和及时的鼓励与激励，同时精讲细评的起点应该始于学生的最近发展区，面向全体学生，与学生的思维合拍，从而产生共鸣，真诚、平等地与学生交流、合作，从而使学生的解题技巧得以提升，解题经验得以挖掘和积累，应试能力得以提升.

以试题为载体“借题发挥”

以试题为载体“借题”发挥应该是对学生可持续发展的终生教育，应该着力于学生良好习惯的养成；更应该促使学生辨别真伪慧眼的炼成、思维能力的提升、分析与解决问题能力的提高、解题技巧的提炼，形成健全的知识体系.

1. “以题”理知

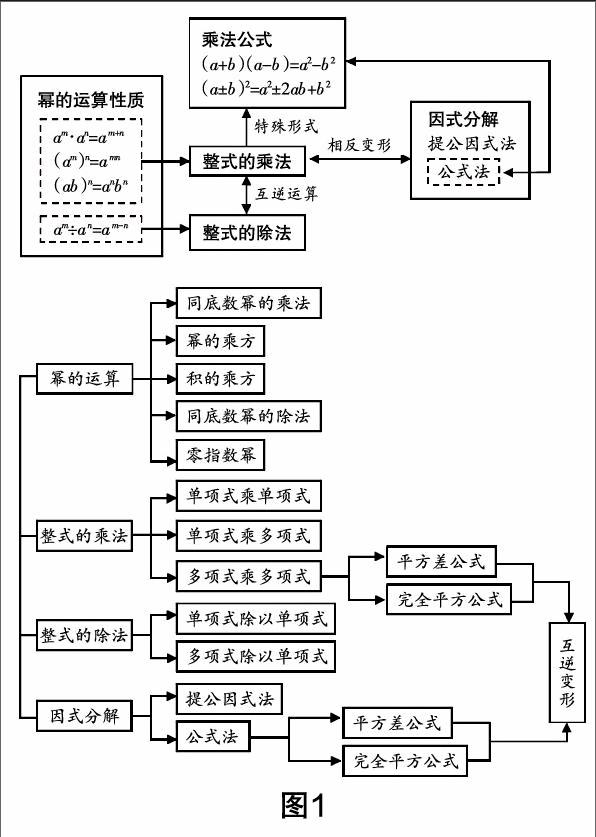
练习是为了对学生的知识掌握情况进行查漏，讲评是为了对学生的知识掌握情况进行补缺. 为此，教师不应只将数学概念、法则、定理等进行简单、枯燥地重复呈现，而应“借题”理知，在讲评时以试题为载体，让学生在具体的情境中引领学生对认识的模糊的概念重新建构，通过典型的例题呈现、分层问题的驱动，使得学生对理不透的定理、法则等作进一步的加深与理解. 当然，为了学生对所学知识有深入的掌握，我们必须让学生建立健全的知识体系，如图1，在“因式分解与整式乘法”复习试题讲评时，可以让学生合作完成形象、生动的知识网络图，使得知识点结构化、系统化，全方位地为学生展现数学学科表达的多元化，使得学生掌握本章内容的同时，有更广阔的思维空间. 同时，“借题”呈现、操作训练等能在帮助学生回忆知识的同时建立属于自己的知识网络、结构图，并养成定期梳理知识的习惯.

2. “借题”理法

为了让学生养成仔细阅读试题的好习惯，我们应该让学生学会圈画关键词，以正确获取试题的所有信息；为了让学生克服思维定式，养成全面思考问题的好习惯，我们应该以学生的“错题”为载体，精心设计讲评方案. 例如对试题“若（x+1）x+6=1，则x=______. ”的处理，首先应让学生呈现自己的思维. 学生A：因为1的任何次幂都是1，所以我的答案为x=0. 学生B：因为a0=1，那么x=-6. 此时笔者没有给予任何评价，而是随机提出问题：“若（x+3）x+6=1，则x=-6，为什么？”“若（x+6）x+6=1，则x=-5，为什么？”“若（x+3）x+6=1，则x=-4，为什么？”“若（x+3）x+8=1，则x=-4，为什么？”并追问：“在解决此题时，我们应该从哪几方面思考？有哪些注意点？”学生小组合作交流后获取了解决这个问题结果的同时，能让学生体验如何全面思考. 最后，笔者还适时进行了拓展思考：“若（x+6）x2-2x-15=1，那么x=______. ”

为了发挥试题的作用，我们要引导学生对错题的错因进行反思与方法提炼，例如：“已知点A（-3，y），B（-1，y），C（2，y）都在反比例函数y=（k>0）的图像上，那么y，y，y的大小关系为______. ”在讲评中，可以以试题为载体设置问题：①请说出你判断的依据和方法；②对于这类题，我们有效的思维方式有哪些？在学生通过反思明确自己错因的同时，能感悟数学的美，提高学生概括、归纳的能力. 随后笔者追问：“已知点A（1，y），B（2，y），C（-1，y）都在反比例函数y=的图像上，那么y，y，y的大小关系为______.”将同一类型的函数问题串联起来进行联想、类比、转化，不仅可以激发学生的兴趣，还能调动学生学习的积极性，同时，发展学生的数学思维，提高学生分析问题、解决问题的能力.

3. “变题”促能

数学教学的实质是数学思维的训练和养成，所以我们在讲评试题时应该充分暴露学生的思维，使得学生明确自己的思维断点或错误所在；同时，关注解决此类问题的解题思想和技巧，训练学生数学思维的发散与创新. 例如，“直线y=x-2与坐标轴围成的三角形的面积为______. ”讲评时，笔者设置了如下问题：①解决这个问题的关键是确定______；②解决这个问题的数学思想为______. 设置问题的目的是为了让学生明白解决此类问题的关键是“数形结合”，即画出符合题意的图形的同时，确定直线与坐标轴围成的三角形的直角边的长度.

变式1 已知直线y=x-b与坐标轴围成的三角形的面积为6，那么b=______.

变式2 已知直线y=kx-2与坐标轴围成的三角形的面积为6，那么k=______.

变式3 已知经过点（1，-1）的直线y=kx-b与坐标轴围成的三角形的面积为6，那么k=______，b=______.

变式训练让学生明白这组题的区别的同时，知道其根本的解题方法没变，于是共同归纳出：用字母表示直线与坐标轴围成的三角形的直角边的长度，并用方程（组）的方法解决此类问题. 如此通过设置易错题的“变题”的训练，使得学生分析问题、解决问题的能力得以提升.

4. “创题”升华

根据学生的错题，围绕考查知识点的基础问题、易错点等“创题”并适当拓展，其目的是教师及时了解试题讲评的效果，让学生获得成功体验，激发学生的学习兴趣. 操作时要注意：①“创新题”的设计要有层次感和针对性；②“创新题”要控制在学生10分钟左右当堂完成；③要注意对结果进行评价、反馈，对学生练习中有创见的地方要给予肯定，对暴露的问题要及时矫正，不要怕学生出错，要在学生明白了自身的知识不足后，对其中暴露的缺陷和不足尽量当堂矫正，引导学生纠正过来.

总之，在试题的讲评课堂中还要创设以自主探究为基础、以合作探究为过程、以全员对话为主体的学习活动，从而使学生的学习积极性得到有效调动，使生生、师生、生师之间的思维碰撞、知识融合、情感互通得到促进，实现高效的、理想的数学试卷讲评课堂.