例谈校本作业中开放题的设置策略

（连江文笔中学，福建福州350500）

例谈校本作业中开放题的设置策略

陈维乐

（连江文笔中学，福建福州350500）

在日常教学中，为更好地开拓学生思维的广阔性和发散性，培养学生的创新意识，需要教师在校本作业中设置一定量的数学开放题。本文通过若干个实例阐述了数学开放题在校本作业中设置策略，以及它在提升学生思维水平方面的作用。

数学开放题；校本作业；思维；案例

一、两个概念

1.数学开放题

戴再平对数学开放题给出了一个描述性的界定：数学开放题是指那些答案不唯一，并在设问方式上要求学生进行多方面、多角度、多层次探索的数学问题。

2.校本作业

所谓校本作业，是指教师从所在校的生源具体情况出发，结合学校师资的传统优势，所开发或者选编出来，能很好体现本校特色且适合学情的作业。

二、研究的意义

作业是教育活动的一个重要组成部分，它既是教师教学活动的一个重要环节，又是学生对所学知识进行巩固的有效途径。但目前数学作业长期被封闭题所霸占，鲜见开放题，这种单一的题目模式不利于学生创新意识的培养。而数学开放题具有“条件可以冗余或不足；答案不要求唯一确定，甚至可以无终极的答案；解题方法可以丰富多样”等特点，它能给学生提供广阔的平台，让他们充分发挥创造性。因而，数学开放题很好地弥补了现阶段校本作业中封闭有余、开放不足的缺憾，让校本作业在开拓学生思维的广阔性和发散性方面发挥更大的作用。

三、开放题设置策略

在校本作业中设置一定量的数学开放题是有意义的，我们该如何设置，在哪些环节设置？下面笔者着重从校本作业中常见的几个环节的设置策略和作用，结合实例予以阐述。

1.用在新课引入环节

通过设置开放问题，展开讨论，逐步引入新课课题，是新课引入常见的一种形式，但常常因为一些知识学习时间间隔过久而冷场，或因为问题的开放性较大，学生参与的“热情”过度，导致教师无法很好地掌控课堂教学进程，完成预定教学任务。针对这一问题，笔者在某些需要大量讨论的课尝试将引入环节前置，即在课前布置预习作业，以期更好地掌控课堂教学进程。例如在学习《正弦定理》前笔者以开放题的形式布置了一道预习作业：

【例1】一般地，把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。初中我们已经学习过关于三角形中这些元素的哪些关系？你能对此进行分类吗？

该设问类似于头脑风暴，若放在课堂上讨论，必将占用较多的时间。由于将引入环节前置，上课时笔者在学生汇报后，给予了简单点评，归纳出如下五个关系：①三角形内角和等于180°（对一般三角形中角与角关系的定量刻画）；②大边对大角，大角对大边（对一般三角形中边与角关系的定性刻画）；③两边之和大于第三边，两边之差小于第三边（对一般三角形中边与边关系的定性刻画）；④勾股定理及其逆定理（对特殊三角形中边与边关系的定量刻画）；⑤锐角的三角函数（对特殊三角形中边与角关系的定量刻画）。通过归纳，引导学生明确已做过的研究工作——特殊三角形中边与边、边与角的定量刻画，这时再提出“能否对任意三角形中边与角的关系进行定量刻画呢？”引入课题就显得水到渠成了。接着，在讨论锐角三角形和钝角三角形情形（未研究过的）时，可自然地通过作高将三角形化归为两个直角三角形（已研究过的）进行研究。

这样的处理，既保留了探究新定理所需要的观察、分析、类比、归纳、推理，又让课堂教学进程变得更加可控。

2.用在新知巩固环节

新学了一个知识点，需要一系列多层次的作业进行巩固，加深对新知的理解。对于定义、概念，我们需要对其辨析，弄清关键词；对于定理、公式，我们常常关注该定理或公式使用有何前提条件，适用于什么样的问题。在设置作业时，除了机械记忆，还应设置反例辨析（如判断题），或者应用小综合（如开放题），追求对新知本质的理解。笔者在《正弦定理》课后设置了这样一道开放题。

【例2】在△ABC中，给出如下条件：

①a=6；②c=3+1；③A=60°；④B=45°。

从上述条件中选择三个条件作为已知条件，利用正弦定理解三角形。

要解决本题，不仅要会用正弦定理，而且还要明确正弦定理所适用的情况：1.已知两角一边，解三角形；2.已知两边一对角，解三角形。从学生答题情况来看，大多数同学均能选择正确的方案，但只有一半的同学能通过判断，选择更易计算的方案①③④或②③④。这体现了不同思维层次的学生对问题思考深刻程度的不同，通过比较，让学生很好地感受到“只有多思才能少算”。多做这样的训练，学生在做题目时就会更愿意去思考，选择更优的解题途径，而不是盲目地下笔。

3.用在知识复习环节

在阶段学习后，如章末、期中、期末等时间点，我们要对所学知识与方法做一归纳小结，帮助学生进行梳理，形成知识网络，以达到融会贯通。下例是笔者针对必修四复习设计的一道开放题，意在引导学生对求角度问题做一梳理。

【例3】如图1所示，在正方形ABCD中，点E为边AB的中点，线段AC与DE交于点P，求∠APD的某个三角函数值。

本题背景熟悉，条件简洁明了，表达通俗易懂，有着“起点低，入口宽，多层次”的特点。以常见正方形为背景，让学生可以多角度使用平面几何知识来辅助解题；入口宽，让学生可以利用不同的方法刻画∠APD，从而求出某个三角函数值；不同的视角带来不同的计算量。在实际训练中，学生对本题的研究表现出很高的热情，提供了多种解法，笔者将它们归纳为如图2所示的几个思路：

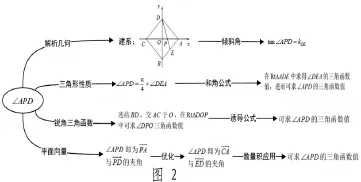
值得一提的是，在确定点P位置时，还呈现出利用△AEP∽△CDP、点P为△ABD重心、向量分解“算两次”、直线方程求交点等不同的精彩。在这些解法中，涉及了平面几何、解析几何、三角恒等变换、平面向量的应用等知识与方法，理顺了求角的几种常见思路。毋庸置疑，这样的复习必将对学生加深知识与方法的理解，乃至融会贯通起到积极的推动作用。

4.用在分层作业环节

让学生学有用的数学，让不同层次的学生都得到发展，是我们一直在追求的目标。如何在校本作业中设置分层作业，而不让学困生产生自卑心理，笔者做了一些有益的尝试，例如下题。

【例4】判断函数f(x)=log2x-的零点个数，并指出其零点所在的大致区间（所给区间长度短者为佳）。

本题在判断零点个数时，既可从“形”出发，通过观察函数y=x与y=的交点情况予以判断，也可从“数”出发，利用f(x)为增函数，借助零点存在性定理予以解决。对于零点所在的区间，能力较低的学生可以通过判断f(1)=0-1＜0，f(2)=1-＞0，推得零点x0ϵ(1,2)。能力中等的学生由二分法可知，可继续判断的符号，通过变形和放缩得到，推得零点能力高的学生以此类推，可继续判断，甚至更为精确。

本题解法不单一，随着零点所在区间长度的缩短，对函数值符号的判断难度增大，但各种水平的学生都有机会作出回答。这样的分层作业既考虑到学生学业水平层次的不同，又在相同的题目背景下让每个学生都能作答。

5.用在解题反思环节

美籍匈牙利数学家乔治·波利亚说过：“数学问题的解决仅仅只是一半，更重要的是解题之后的回顾。”只有学会解后反思，才能举一反三，触类旁通，从而脱离题海战术之苦。在必修3第一章学习程序框图设计时，“设计一个计算1+2+…+100的值算法”是课本上的一道例题，它是一类数列求和或求积问题的母题，它对学生深刻地理解算法思想和程序框图的设计起着非常重要的作用，教师有必要引导学生对该例题进行更为深刻地研究与反思。基于此，笔者在《程序框图的画法》这一节课后作业设计了如下一道开放题。

【例5】如图3的程序框图是计算1+2+…+100的值的一个算法，这是循环结构应用的一个重要实例，在此基础上进行微调即可解决一类求和、求积的问题。如只要将③处改为S=S+i2，该算法即可用于计算12+22+…1002的值。类似的有：

（1）将②处改为_____，③处改为_______，可用来计算1×2×…×99×100的值；

（2）请类比上述例子，改动如图3程序框图中的若干处（不超过三处），解决一个求和或求积问题。

该题以课本例题为母题，通过举例示范，演示循环结构在求和、求积问题中的应用，通过多层设问，引发学生进行解题反思，主动对一道题目进行适当的类比、引申、拓展。这不仅能让学生直击问题的核心，而且能激发学生的探究热情，提高他们的解题能力。

以上几个案例说明，数学开放题能给学生更多的思考空间，它有利于学生对知识的主动建构，获得认知结构的改造和重组。在校本作业中设置数学开放题，必将对开拓学生思维的广阔性和发散性，培养其创新意识起到积极的作用。

本文系福建省教育科学“十二五”规划2013年度课题“基于人本理念的高中数学校本作业模式研究”（项目编号：FJJKXB13—170）阶段性研究成果。