巧用反例点拨课堂——浅析初中数学教学中反例的运用

江苏省盐城市大丰区城东实验初级中学 李宏魁

巧用反例点拨课堂
——浅析初中数学教学中反例的运用

江苏省盐城市大丰区城东实验初级中学 李宏魁

在初中数学的教学中，反例教学法起到了很重要的作用，反例的运用有助于初中生巩固学习过的数学概念和定理，在一定程度上也能增加学生学习数学的兴趣。在教学方面也能有效提高教学质量，在反例的解答过程中，学生对于知识点的理解也会更加深刻。因此在初中数学的教学过程中，反例的运用是十分重要的，同时在运用反例的过程中也要注重方式方法，将有利的一面更加扩大。

一、反例教学法，培养思维缜密性

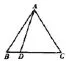
数学是一门严谨的科目，在学习数学的过程中能够很好地培养思维的严谨性，在生活中也能看出来，数学学得好的人思维都非常缜密。有时在写数学题时也会有这样的情况出现：这道题明明会做却拿不到分数，之后发现，就是因为自己太马虎才丢了这道题的分数。在考虑问题和解决问题的时候，要做到严谨而又全面，这就是学好数学的关键所在，而恰好反例教学法能够培养并提高学生思维的严谨性，通过对反例的探讨发现问题所在，在遇到一道数学题很难从正面解答时，也可以利用反例教学法，换一个角度看问题，从反面还能使思维变得更加灵活，尤其是在辨别真假命题时，反例法能够更快地解决问题，举一个例子：“证明两个无理数的积仍然是无理数”这一个命题是否为真命题时，大多数学生会举出这样一个例子来证明为无理数，这样看来这个命题是真命题，但是这个答案是错误的，这时就应该举出一个反例，2就是一个有理数，这样看来这个命题就是假命题。再举一个例子，在学习三角形时经常需要判断两个三角形是否全等，教师向学生提出疑问：“在两个三角形中，有一个角相等，两条边相等，那么这两个三角形是否全等？很多同学都知道不一定是全等的，但是具体的原因不是很清楚，这时教师就可以使用反例法进行教学，如图所示，在这个图中边AB=AC，但是不全等。这个题中教师就很好地运用了反例的方法，使得学生们更好地理解了为什么一个角相等，两条边也相等的两个三角形不是全等的。同时也培养了学生思维的缜密性。

二、反例教学法，增强数学知识的运用

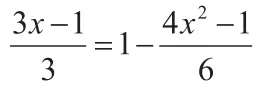
三、反例教学法，激发学生创新精神

社会需要不断地发展，在社会发展的大背景下，创新精神显得尤为重要，创新型的人才也是以后社会所需要的。在初中数学的教学中，也需要注重学生创新精神的激发，很多学生的潜力都是无限的，但是没有被激发出来，运用反例教学法，能够更好的激发学生的创新精神。比如在面对一个真命题时，教师会引导学生进行思维的发散，从中会产生许多的命题，关于命题的真假，是需要学生进行讨论的。在证明这些命题时，如果从正面很难解决，那么就可以选择反例法进行论证。教师可以向学生构建一个反例思维的方式，实现反例构建与整体推理过程的完美结合，以此培养学生的创新思维。举一个例子，很多学生在认识了正三棱锥之后，会产生一个认识：若一个三棱锥的底面是正三角形，侧面均为等腰三角形，那么这个三棱锥是正三棱锥。这个命题是错误的，很多同学都忽略了这个条件“侧面是全等的等腰三角形”如果这个三棱锥的底面是正三角形，但是侧面等腰三角形的腰长并不是全部相等的，这个三棱锥就不是正三棱锥了。通过这个反例地探索，学生也会从中感受到创新思维的快乐，在数学的学习中一味地循规蹈矩会限制住学生自己思维的成长，因此就需要创新来打破这一局面，从而提高学生解决数学问题的能力，也同时激发了学生对数学学习的兴趣。与此同时教学效果也大大提高了。

综上所述，在初中数学的教学过程中合理的运用反例教学法，不仅是对学生综合能力的提高能够起到很大的作用，而且也会让教师的教学模式变的更加丰富多彩，增加学生对数学的兴趣，反例教学方法也能更好地提高教学效率。