一道高考题的研究
江苏省海安县实验中学 潘新峰
一道高考题的研究
江苏省海安县实验中学 潘新峰
掌握数学就意味着善于解题。高考考场上遇到新问题,总想用熟悉的题型去“套”,这样极有可能解不出来,或耗费大量的时间。2015届江苏考生普遍认为第18题难繁,其实本题只要方法得当,不失为一道不错的中档题。
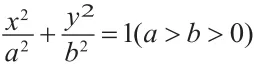
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,若PC= 2AB,求直线AB的方程。
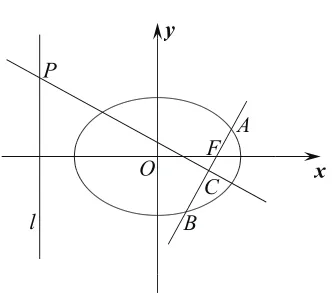
下面给出第(2)问的解法与大家探讨。
分析思路1:直线AB的方程有两种设法,y=k(x-1)或x=my+1。弦长有两种求法,(这个在高考解题中要证明)。当然具体解题过程中也可以利用韦达定理,稍微简化一点运算。下面以江苏高考试卷给出的参考答案说明以上思路。
(2)设直线AB的方程y=k(x-1),当AB⊥x轴时,,又CP=3,不合题意。
当AB与x轴不垂直时,设直线AB的方程为y=k(x-1),,将AB的方程代入椭圆方程,得,则方程的解为,C的坐标为,且。此处还可以用,也可以直接。
若k=0,则线段AB的垂直平分线为y轴,与左准线平行,不合题意。
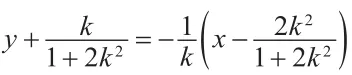
分析思路2:江苏高考试卷命题组给出的参考答案思路可行,但方法不是最佳。要想快速解决本题,两条线段AB、PC的长度千万不能分开研究,在平面直角坐标中,两条线段平行或共线,则它们在同一条坐标轴上射影之比等于原线段长度之比;在平面直角坐标系中,如果两条线段互相垂直,那么它们分别在两个坐标轴上的射影之比等于原线段长度之比。这是两个简单的事实。

例题选讲:已知抛物线C1:的焦点F以及椭圆C2:的上、下焦点及左、右顶点均在圆O:上。
(1)求抛物线C1和椭圆C2的标准方程;
(2)过点F的直线交抛物线C1于不同的两点A,B,交y轴于点N,已知,求的值;

在解析几何中,线段关系常有两种形式出现∶①AB=λ,②AB=λCD(其中λ为常数),第一种形式常用思路1,但运算量稍大。第二种形式,我们常常把线段或向量投影到坐标轴。由此可见,学生在平时的学习中,必须搞好“思路可行”与“方法最佳”的关系。

