基于聚类-实测风功率曲线的风电场等值模型研究

沈清野,沈清坤,秦本双

(东北电力大学 电气工程学院,吉林 吉林 132012)



基于聚类-实测风功率曲线的风电场等值模型研究

沈清野,沈清坤,秦本双

(东北电力大学 电气工程学院,吉林 吉林 132012)

针对风电场工作环境,提出了一种基于聚类-实测风功率曲线相结合的方法构建风电场等值模型。以每台机组所获得的风速作为分群指标进行机组数据划分,运用K-means聚类算法将风电场内具有相近运行特性的机组分为一类,将同群机组等值为一台风力发电机,并利用分层抽样的方法求取实测风速-功率特性曲线,建立了风电场输出功率仿真模型。算例分析表明,该方法与传统依据标准风速-功率特性曲线的方法相比提高了模型精度。

聚类算法;K-means;风速-功率特性曲线;机群

随着中国风电并网容量的不断增大,风电功率波动对电网影响愈加显著[1-3]。因此,风电场输出功率建模已成为国内重要研究课题。大型风电场由于机组数目较多、地形地貌复杂、机组排列方式不同,使得风电场内机组之间受到尾流效应的影响较为严重,导致风电场内机组所获得的风速存在较大差异,而且风电场经常处于复杂多变的风况下,这又使得每台风电机组并非严格按着厂家给定的风功率曲线运行。很多文献对此进行了大量研究[4-12]，在此基础上,为了提高等值模型精度,本文提出了基于聚类-实测风功率曲线相结合的方法,运用K-means聚类算法对大型风电场机组实测数据进行聚类划分,将同群机组等值为一台风力发电机,并采用分层抽样的方法,得到等值风电机组的实际风速-功率特性曲线,从而建立了整个风电场等效风速-功率模型。

1 风电机组风速-功率运行特性曲线

传统的风电场建模方法往往依赖于厂家提供的风电机组风速-功率特性曲线,此曲线是按照国际电工委员会的IEC61400-12标准遵从技术手册给定的特定运行条件而获得的,该曲线表示的是风速与功率10 min平均值的关系。然而,风电机组的实际运行环境与在理想状态下的设计环境存在很大差别。如果直接采用厂家提供的标准风速-功率特性曲线进行建模会产生很大误差,对模型的精度会有很大影响。

某机型的机组主要技术参数如表1所示,其中切出风速为25 m/s。根据表1参数可大致对风电

表1 机组的主要技术参数

机组运行的实测数据进行预处理,剔除一些大于切除风速和风速值为负值的数据,利用这些数据分析会给模型带来误差。

利用表1风电机组的主要技术参数以及厂家所提供技术手册中的风速-功率序列对数据绘出了标准风速-功率特性曲线,如图1所示。

图1 MY-1500厂家提供的标准风速-功率特性曲线

Fig.1 Standard wind speed-power characteristic curve provided by MY-1500 manufacturers

从图1可以看到,风速V与输出功率P为一一对应的函数关系。由于大型风电场内风电机组数目众多,风电场占地面积较大,存在风电场内各机组风能分布不均的现象,而且风电机组常运行在风速和风向不断变化的情况下,所以其实际运行状况不是严格遵从厂家提供的标准风速—功率特性曲线运行。

2 求取风电机组实际运行特性曲线

为了获取能够真实反映风电场实际运行状态的风速-功率特性曲线,需要根据风电场的实测数据得到风电场运行的动态散点。任意选取风电场中某一运行机组的实测数据,绘出其风速与功率对应的实际运行散点和厂家提供的标准功率曲线,如图2所示。

从图2可以看到,该风电机组实际的风速与功率对应坐标点不是严格落在标准特性曲线上,而是运行在一个较宽的区域内,所以需运用数理统计方法找出风电机组每一个功率值对应的出现概率最大的风速值,并将这些点连起来得到概率最大的风速-功率曲线。此曲线可作为反映风电机组实际运行的风速-功率特性曲线。

图2 机组实际运行散点与厂家提供的标准 风速-功率特性曲线

从风电场中任意选取一台风电机组风速和功率作为数据输入量样本,将风速和功率编辑成时间序列一一对应的数据对(Vi,Pi)。为了获取真实的风电机组风速-功率特性曲线,需要对图2实际运行的散点进行处理,求取实测功率曲线的步骤如下:

1) 预处理所需要的风速和功率数据对。

2) 风电机组额定功率为1500 kW,采用分层抽样法,将0～1480 kW以40 kW为单位进行分层,分层时只考虑小于额定功率的情况,因此按照功率将风速-功率数据分成不同的层Ni(i=1,2,…,37)。

3) 在Ni中随机抽取一个很小的功率区间(Pai,Pbi),其中(Pai,Pbi)∈Ni,因Pbi-Pai≪PN,故认为该区间内的所有风速都同时对应一个功率值Pai。统计对应功率Pai出现概率最高的风速Vi,即找出了对应该层的实测数据对(Vi,Pai),每一层通过相同方法找出对应该层的实测风速-功率数据对。

通过上述步骤,列出了能够真实反映风电机组运行状态的实测风速-功率数据对,如表2所示。根据表2绘出表征风电机组实际运行的实测风速-功率特性曲线,如图3所示。从图3可以看出,风速与功率之间的函数关系比较复杂。为了便于仿真应用及保证曲线表达的准确性,采用三次样条差值法对所得的(Vi,Pai)数据对进行处理,不仅可以得到表示风速-功率对应关系的光滑连续曲线,而且便于该曲线在仿真中应用。将风电机组的实测曲线、标准曲线、实测V-P散点绘于同一个图中作比较,如图4所示。

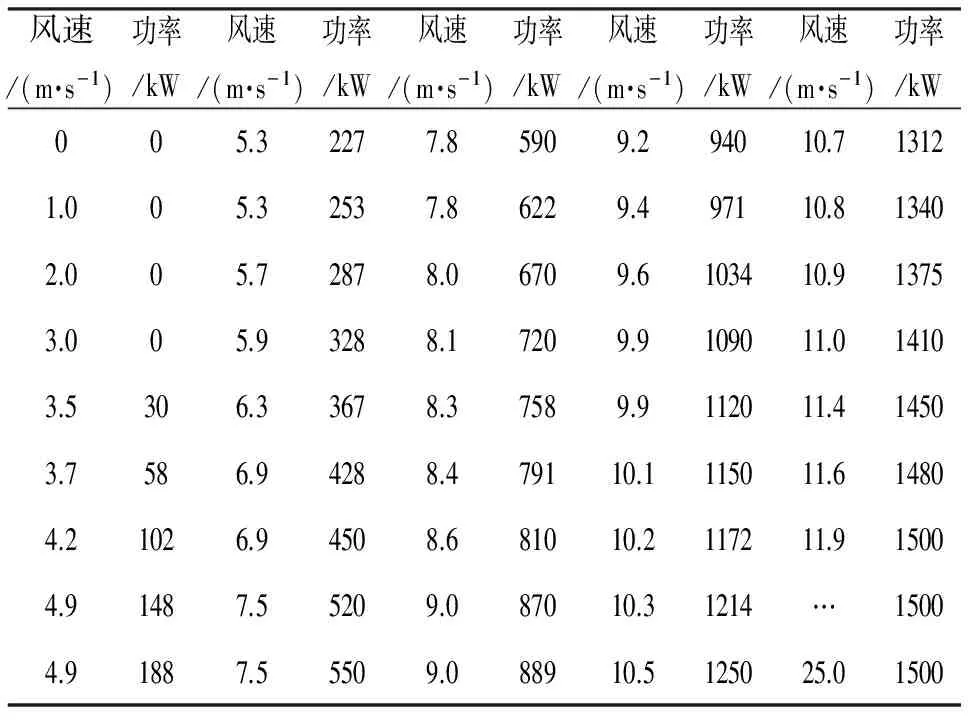
表2 某机组实测风速-功率数据对

图3 某机组实测风速-功率特性曲线

图4 某机组两种风速-功率特性曲线

根据表2及图4可以得出：风速达到12 m/s左右时,风电机组进入额定功率运行区;风速小于 8 m/s时,两条曲线比较接近,但实测曲线略高于标准曲线;风速在8～12 m/s时,实测曲线明显比标准曲线低得多。因此,如果采用标准曲线建模,会带来较大误差。

3 基于K-means聚类算法划分机群

由于风电场风能分布不均,各机组之间所获风速存在较大差异性,为了提高模型精度,需要运用K-means聚类算法将风电场内的机组进行机群划分,步骤如下:

1) 数据处理。选取并网运行的机组数据,剔除因故障而停机的机组数据。

2) 机组分群指标的选取。以风速作为分群的指标,风速在该段时间的采样点为m个,编辑所要建立模型时间段内的风速矩阵为

其中,V(i,j)表示第i台风电机组在第j个时刻测得的风速。将向量Vi看作空间V的一个样本组,V中样本数量为n,维数为m。

3) 将所有样本组分为k个簇,即k个机群。任意选择k个样本组作为k个簇Ga的初始聚类中心,则样本点中心形式为

Va=(Va,1,Va,2,…Va,m)

式中:a=1,2,…,k;Ga为第a个簇样本集合。

4) 计算任意一个样本点V(i,j)到k个聚类中心的欧氏距离为

将所有样本组Vi划分到使欧式距离d最小的簇Ga中,遍历所有的样本组,完成第一次划分。

5) 计算每个簇中的样本均值,并计算标准测度函数,其计算表达式分别为

6) 以每个簇的样本均值新的初始聚类中心,重复步骤4)～步骤6),直到标准测度函数收敛。

通过上述步骤,选取各个簇中使得欧式距离d最小的机组作为代表各个机群的等值机组,一共选出k台等值机组来表征各个机群,由此可得风电场输出功率计算模型为

(1)

式中:Pea表示第a号机群中等值机组的输出功率,Na为第a号机群中的机组台数。

4 算例分析

以吉林省西部某大型风电场实测数据为依据,该风电场拥有同型号35台MY-1500 KW机组,占地面积较大,风资源丰富,风机布局如图5所示。

图5 某风电场风机布局图

选取数据时间为2013-05-13T03:00:00-09:40:00,采样间隔为1 min,数据时间长度为400 min,数据总量为400×35 (分群时m=400,n=35) 组。利用该段时间的实测数据,通过K-means聚类算法将该风电场内的机组进行机群分类,划分为3个机群,划分结果如表3所示。

表3 机群聚类划分结果

从图5和表3可以看出,按风速分群结果表明距离相近的风电机组风速大小不一定相近。如1号机组和2号机组,虽然地理位置相距较近,但也有可能因风速差别较大被分到不同的群内,而2号和35号机组,地理位置相距较远,但也有可能因风速变化相近被分到同一个群内。

通过聚类算法划分机群后,得到了各个样本组距离聚类中心的欧式距离d,以欧式距离d最小为原则选取表征3个机群的等值机组。表3中Ⅰ号机群中的5号机组、Ⅱ号机群中的16号机组、Ⅲ号机群中的2号机组距离聚类中心的欧式距离最小,因此选取5号、16号、2号机组表征整个风电场。

通过求取风电机组实测风速-功率特性曲线的方法,得到了3台等值机组的真实反映风速-功率运行特性曲线,然后根据求得的实测风速-功率曲线得出计算等值机组输出功率的仿真模型,再根据式(1)可以得到风电场输出功率的计算模型。

分析并比较基于聚类算法-实测风电功率特性曲线建模与传统建模采用厂家标准功率曲线模型精度差别,结果如图6所示。

图6 三种输出功率曲线对比图

从图6可以看出,本文方法的输出功率曲线更逼近实测功率曲线,精度相比传统方法有所提高。本文方法的输出功率与实测功率的误差时序如图7所示。

图7 输出功率与实测值的误差时序图

从图7中可以看出输出功率与实测功率的相对误差基本小于10%。基于聚类算法-实测风功率曲线与传统厂家提供的标准风速-功率特性曲线的误差统计对比如表4所示。

表4 误差结果分析

从表4可以看出,传统方法平均相对误差为9.34%,而本文方法的平均相对误差为5.64%。

5 结 论

1) 通过求取能够反映风电机组实际运行状态的实测风速-功率特性曲线,发现标准特性曲线与实测特性曲线在一定风速范围内存在较大差异。

2) 基于K-means聚类算法将风电场机群划分时,发现各机组地理位置相近风速值大小不一定相近,相矩较远的机组也有可能被分到同一个机群。

3) 以相对误差作为衡量模型精度指标,计算得出本文方法平均相对误差为5.64%,相比传统建模方法在精度上有了很大提高。

[1] 迟永宁,刘燕华,王伟胜,等. 风电接入对电力系统的影响[J]. 电网技术,2007,31(3):77-81. CHI Yongning,LIU Yanhua,WANG Weisheng,et al. Study on impact of wind power integration on power system[J]. Power System Technology,2007,31(3):77-81.

[2] 张红光,张粒子,陈树勇,等. 大容量风电场接入电网的暂态稳定特性和调度对策研究[J]. 中国电机工程学报,2007,27(31):45-51. ZHANG Hongguang,ZHANG Leizi,CHEN Shuyong,et al. Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms[J]. Proceedings of the CSEE,2007,27(31):45-51.

[3] 杨国生,李欣,周泽昕. 风电场接入对配电网继电保护的影响与对策[J]. 电网技术,2009,33(11):87-91. YANG Guosheng,LI Xin,ZHOU Zexin. Impacts of wind farm on relay protection for distribution network and its countermeasur-es[J]. Power System Technology,2009,33(11):87-91.

[4] 郎斌斌,穆钢,严干贵,等. 联网风电机组风速-功率特性曲线的研究[J]. 电网技术,2008,32(12):70-74. LANG Binbin,MU Gang,YAN Gangui,et al. Research on wind speed vs output power characteristic curve of wind power generator interconnected with power grid[J]. Power System Technology,2008,32(12):70-74.

[5] 米增强,苏勋文,杨奇逊,等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报,2010,25(5):162-169. MI Zengqiang,SU Xunwen,YANG Qixun,et al. Multi-machine representation method for dynamic equivalent model of wind far-ms[J]. Transactions of China Electrotechnical Society,2010,25(5):162-169.

[6] 陈树勇,王聪,申洪,等. 基于聚类算法的风电场动态等值[J]. 中国电机工程学报,2012,32(4):11-19. CHEN Shuyong,WANG Cong,SHEN Hong,et al. Dynamic equivalence for wind farms based on clustering algorithm[J]. Proceedings of the CSEE,2012,32(4):11-19.

[7] 严干贵, 李鸿博, 穆钢, 等. 基于等效风速的风电场等值建模[J]. 东北电力大学学报,2011,31(3):13-18. YAN Gangui,LI Hongbo,MU Gang,et al. Equivalent model of wind farm by using the equivalent wind speed[J]. Journal of Northeast Dianli University,2011,31(3):13-18.

[8] 曹娜,赵海翔,任普春,等. 风电场动态分析中风速模型的建立及应用[J]. 中国电机工程学报,2007,27(36):68-72. CAO Na,ZHAO Haixiang,REN Puchun,et al. Establish and application of wind speed model in wind farm dynamic analysis[J]. Proceedings of the CSEE,2007,27(36):68-72.

[9] 王钤,潘险险,陈迎,等. 基于实测数据的风电场风速-功率模型的研究[J]. 电力系统保护与控制,2014,42(2):23-27. WANG Qian,PAN Xianxian,CHEN Ying,et al. Study of wind speed-active power model for wind farm based on measured da-ta[J]. Power System Protection and Control,2014,42(2):23-27.

[10] 朱乾龙,韩平平,丁明,等. 基于聚类—判别分析的风电场概率等值建模研究[J]. 中国电机工程学报,2014,34(28):4770-4780. ZHU Qianlong,HAN Pingping,DING Ming,et al. Probabilistic equivalent model for wind farms based on clustering-discriminant analysis[J]. Proceedings of the CSEE,2014,34(28):4770-4780.

[11] 黄梅,万航羽. 在动态仿真中风电场模型的简化[J]. 电工技术学报,2009,24(9):147-152. HUANG Mei,WAN Hangyu. Simplification of wind farm model for dynamic simulation[J]. Transactions of China Electrotechnical Society,2009,24(9):147-152.

[12] 侯佑华,齐军,王小海,等. 大规模风电场的建模及其在内蒙古电网安全稳定运行的研究[J]. 中国电机工程学报,2010,30(4):71-78. HOU Youhua,QI Jun,WANG Xiaohai,et al. Modeling of a largescale wind farm and the studying for its security and stability operation in inner mongolia grid[J]. Proceedings of the CSEE,2010,30(4):71-78.

(责任编辑 郭金光)

Research on equivalent model of wind farm based on clustering algorithm-wind speed vs output power characteristic curve

SHEN Qingye, SHEN Qingkun, QIN Benshuang

(Electrical Engineering College, Northeast DianLi University, Jilin 132012, China)

Aiming at working environment of wind farm. A method based on clustering algorithm combined with wind speed vs power characteristic curve is proposed for constructing equivalent model of Wind Farm. according to wind speed of each wind turbine was adopted as a cluster classification index to divide the data of wind turbines, the similar operation characteristics of wind turbines within wind farm were divided into a same group by using K-means clustering algorithm, and the wind turbines in the same group were equivalent as a wind generator, stratification sampling is used to get the real wind speed vs output power characteristic curve, the simulation model of wind farm was constructed. It improves the model of precision which compares with traditional method relying on the Standard of wind speed vs output power characteristic curve.

clustering algorithm; K-means; wind speed vs power characteristic curve; cluster

2015-07-31。

沈清野(1990—),男,硕士研究生,研究方向为风力发电运行与控制。

TM614

A

2095-6843(2016)02-0114-05