计及风电的中长期机组检修计划研究

雷 宇

(71496部队,山东 烟台 265800)



计及风电的中长期机组检修计划研究

雷 宇

(71496部队,山东 烟台 265800)

为解决大规模风电并网使电力系统出现低谷时段大量弃风的问题,利用主成分分析法和分层聚类技术提取风电各季节出力典型模式,并采用均摊法建立相应的通用生产函数,以及考虑风电出力季节特性的发电机组检修计划优化决策模型。以各时段弃风电量最少和检修成本最小为优化目标,采用粒子群算法对该模型进行求解。实际算例验证,该模型与方法可行、有效,提高了风电消纳能力,在发电机组检修决策时考虑风电出力季节特性能够显著减少弃风。

风电季节特性;机组检修计划;通用生产函数;粒子群算法

风能是清洁无污染的绿色可再生能源,当风电场在电力系统中达到一定比例时,风电场出力的波动性和季节性在某种意义上相当于增大了系统等效负荷的不确定性,从而给常规机组的运行和检修带来较大影响。在中国部分地区,系统调峰能力不足,再加上风电固有的随机性和波动性,如果中长期检修计划中不考虑风电出力,将导致负荷低谷风电大发时刻弃风,影响系统运行的经济性和风电的可持续发展[1-3]。所以中长期的发电机组检修计划将影响短期上网机组组成,进而影响系统短期机组组合的决策和调峰[4]。

目前,关于考虑风电进行机组检修计划决策的研究主要是利用历史数据拟合风电出力概率曲线，将风电纳入检修计划。文献[5-6]分别用威布尔(Weibull)和beta概率分布函数对风电出力进行拟合，从而制定含风电中长期机组检修计划,一定程度上优化了风电弃风电量,但是对于风电出力的拟合精度较差,不能很好地体现风电的季节出力特性。为此,本文充分考虑风电的季节特性,采用主成分分析法和分层聚类法提取了各季节风电出力典型模式,建立了各季节风电出力通用生产函数(UGF)模型,即考虑风电出力季节特性进行中长期机组检修计划决策,在安全约束条件下,以弃风电量最少和检修成本最低为优化目标,有效降低系统弃风电量,提高风电利用率。

1 风电的季节特性

风电出力季节特性可以用一年内各个月平均风电出力进行描述。风电各月平均出力与当地的气候、地形和海陆分布等密切相关,不同季节、不同月份变化幅度较大,出力特性存在很大差别,具有明显的季节性[7-8]。

根据长期观测的历史数据,首先采用主成分分析法(principal component analysis, PCA)对风电出力数据进行特征提取,根据主成分的重要性去掉较弱的成分。然后采用分层聚类法对特征提取后的风功率数据进行聚类,获得典型风电出力模式。最后根据提取的典型风电出力模式釆用均摊法建立各季节风电出力的UGF模型[9]。

设风电场k在模式m时段t有n个状态,则描述风电场k在模式m时段t的出力及其概率的UGF模型为

利用上述UGF函数进行含风电场的随机生产模拟可得各季节相应的弃风电量[10]。

2 中长期机组检修计划模型

2.1 目标函数

考虑风电出力季节特性的中长期检修计划模型目标分别是检修成本最小和弃风电量最少。

1) 系统检修成本最低:

式中:Xi,t为机组i在时段t状态,检修时为1,否则为0;ci,t为时段t对应的检修成本；N为发电机组数；T为总时段数。

2) 弃风电量最少:

式中Et为时段t的弃风电量。每个时段的弃风电量根据风电出力UGF函数进行随机生产模拟得到。

采用加权求和将2个目标优化转化为单目标优化问题:

式中w1和w2分别为2个优化目标的权重,关于弃风价值尚未有定论,w1和w2可由决策者根据实际需要确定。

2.2 约束条件

2.2.1 检修时间约束

机组检修必须在一个给定的连续时段内完成,即

Xi,t=1,si≤t≤si+di

Xi,t=0,tsi+di

ei≤si≤li

式中:ei为第i台机组可以开始检修的最早时间段;li为第i台机组可以开始检修的最迟时间段;di为第i台机组的检修持续时段;si为第i台机组的检修开始时段。

2.2.2 检修能力约束

在某一时间段不允许多台机组同时检修,即

式中Nt为第t时段可同时检修的发电机组台数,由检修资源制约。

2.2.3 机组检修间隔、检修次数约束

机组两次检修之间有最小间隔时段约束,机组有一年检修次数约束,即

式中:Bi为机组i在两次检修之间的最小时间间隔;si,k和si,k+1分别为第i台机组第k次和第k+1次检修的起始时段;k为机组i的检修事件集合。

2.2.4 系统运行约束

包括系统功率平衡约束,电网正负旋转备用约束和机组出力上下限约束。

系统应满足发电与用电平衡,即

式中:pi,t为机组i在时段t的有功出力;Wt和Et分别为时段t的风电场输出功率和弃风电量;PD,t为时段t的负荷需求。

火电机组出力应在其出力上下限范围内,即

pi,min≤pi,t≤pi,max

式中pi,min和pi,max分别为机组i的最小、最大出力。

风电弃风量应满足

0≤Et≤Wt

由于风电出力的不稳定,系统需要提供足够的旋转备用容量以应对可能出现的波动。当风电出力不足时需要系统常规火电增加出力,当风电出力过大时需要系统常规火电减少出力。若将风电输出功率的百分比作为系统对风电的备用需求,则算例中设定应为风电功率的25%至40%[11]。由此可知,系统可用正旋转备用(即一个时段内可向上爬坡量和机组出力的可上升空间之中的较小者)不得少于负荷旋转备用和风电备用的和,系统可用负旋转备用(即一个时段内的向下爬坡量和当前机组出力可下降的最大空间之中的较小者)不得少于风电备用量,即

式中:rui和rdi为第i台机组的向上和向下爬坡率;机组爬坡响应时间为10 min记为T10;prt和rwt分别为时段t的负荷备用量(取为负荷的2%)和风电备用量(设定为风电功率的25%至40%)。

3 求解算法

所建数学模型属于多约束条件的非线性优化问题,数值求解有很大的难度。粒子群算法具有广泛的适应性和良好的鲁棒性,搜索机制简单,程序容易实现,收敛速度快。因此本文以各机组开始检修时间列向量为粒子,采用基于连续空间的离散粒子群算法(DPSO)求解[5],即第j次迭代时粒子更新公式为

xi=xi+vi

(1)

式中:int为取整函数;xi为第i个粒子;vi为第i个粒子的速度;pi为第i个粒子的历史最优解;pg为全局最优解;wmax,wmin为惯性系数最大值和最小值;c1,c2为学习因子;r1,r2为0至1之间的随机数。

以机组开始检修时间si为粒子值,故在已知机组检修时长di的情况下,可以确定机组的检修区间为[si,k,si,k+1],确保满足检修连续性约束。对于检修开始时间约束,可采用罚值法。将机组出力上下限约束、系统平衡约束和系统最小备用容量约束,处理为MATLAB求解中的约束条件。

算法具体实现步骤如下:

1) 设定粒子个数Np、最大迭代次数M、惯性系数最大值wmax和最小值wmin、学习因子c1和c2,并随机初始化各个粒子的值和速度,其中常规机组部分粒子为各机组开始检修时间列向量。

2) 根据各粒子的初始值求解各机组出力,即求解特定机组检修计划下的最优出力分配子问题。在特定机组检修计划下,目标函数转变为线性规划问题。

3) 根据目标函数计算各粒子适应值,将适应值最小的粒子设定为初始全局最优解,当前各粒子值设为各粒子的初始历史最优解。

4) 更新粒子值和速度,其中粒子的常规机组按式(1)更新。为防止算法过早收敛,当更新过后新产生的粒子一旦与全局最优解相同,该粒子随机跳变为满足约束的任意值。

5) 计算各粒子所代表检修计划下各机组出力,并计算各粒子适应值。

6) 更新全局最优解和各粒子历史最优解。

7) 判断是否达到最大迭代次数,如果没有达到,返回步骤4),如果达到,结束程序并输出全局最优解。

4 算例分析

采用IEEE-RTS测试系统,对14台常规机组进行一年的检修安排,共52周。设定最大机组检修时间为7周,最小机组检修时间为2周[2,12]。采用某风电场2010年至2013年小时平均的历史风电出力数据,风电接入容量为150 MW。系统的旋转备用需求取8%。风电接入之后,保持系统的旋转备用容量需求及其他机组装机情况不变。全网总装机容量为1000 MW,其中风电场装机容量占15%。设粒子数为30,最大迭代次数200次,wmax=0.9,wmin=0.4,c1=c2=2。

分析算例中风电场出力的季节特性,提取风电4个季节的典型出力模式,并基于典型出力模式建立各时段UGF函数。在此列出各个季节出现概率较大的几种典型出力模式的簇心,称为主模式。不同季节主模式的簇心及其概率分别如表1和图1～4所示。

表1 各季节每种模式对应的概率

从表1和图1～4可以看出,不同模式的时序波动情况不同,出现的概率也不同,亦即不同季节风电出力特性不同,这说明本文提出的方法能较好地提取风电出力季节模式。

图1 春季风电典型出力模式

图2 夏季风电典型出力模式

图3 秋季风电典型出力模式

图4 冬季风电典型出力模式

为直观说明考虑风电季节特性进行检修计划对弃风电量和检修成本的影响,设置如下4种方案:

方案1:考虑检修基本约束和发电可靠性约束,不考虑风电,只对检修成本目标进行优化(即w2=0)。

方案2:考虑检修基本约束、发电可靠性约束和风电的weibull分布,对检修成本目标和弃风量目标进行优化(w1=1,w2=10)。

方案3:考虑检修基本约束、发电可靠性约束和风电的季节特性,对检修成本目标和弃风量目标进行优化(w1=1,w2=10)。

方案4:考虑检修基本约束、发电可靠性约束和风电的季节特性,对检修成本目标和弃风量目标进行优化(w1=1,w2=0.1)。

针对上述4个方案,分别采用粒子群算法安排机组检修,可得每种方案检修费用和弃风电量。

4种方案下的各时段弃风量如图5所示。

图5 不同方案下各时段弃风电量

由图5可以看出,不同方案不同季节系统的弃风电量差别很大,且考虑风电季节特性安排检修计划显著减少了系统的弃风电量。

4个方案的检修费用和弃风电量如表2所示。

表2 不同方案下检修成本和弃风电量比较

Table 2 Comparison of maintenance cost and abandoned wind electric quantity under different schemes

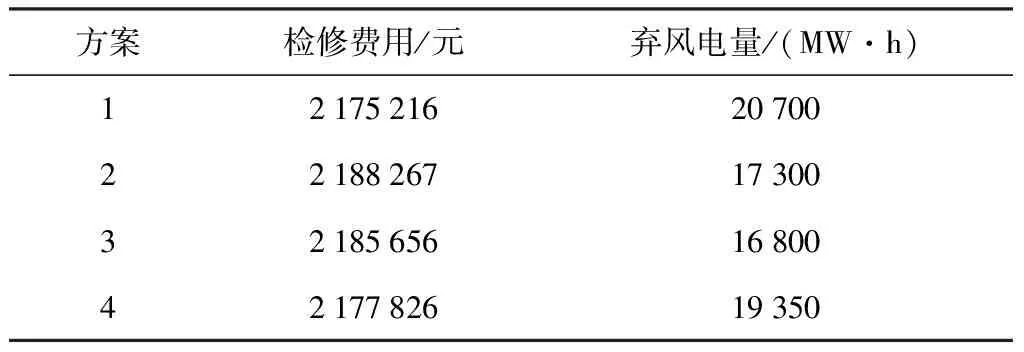
方案检修费用/元弃风电量/(MW·h)1217521620700221882671730032185656168004217782619350

从表2可以看到,在检修决策中考虑风电的出力,相比于不考虑风电的情况,能够减少弃风量,但检修成本略有增加。考虑风电的季节特性比单纯利用概率拟合风电出力更能有效地优化检修费用和减少弃风电量。弃风电量优化目标权重系数越大,即越重视风电的消纳,弃风电量越小,检修成本增加越多。因此考虑风电的季节特性能更科学地进行检修决策,降低弃风电量。

5 结 论

1) 在检修计划决策过程中考虑风电季节特性,能够有效降低弃风电量,减少风电场出力波动对机组检修计划带来的影响,保证可再生能源充分利用。

2) 通过粒子群方法求解多目标非线性优化模型,降低了模型的求解难度,提高了模型的求解效率,为考虑大规模风电的检修计划优化决策问题的应用提供了高效、实用的方法。

[1] 张宏宇, 印永华, 申洪, 等. 考虑大规模风电调峰要求的系统机组检修计划[J]. 电力系统自动化, 2012, 36(16): 25-30. ZHANG Hongyu, YIN Yonghua, SHEN Hong, et al. Generator maintenance scheduling of large-scale wind power integration considering peak shaving [J]. Automation of Electric Power Systems, 2012, 36(16): 25-30.

[2] 苏运, 朱耀明, 张节潭, 等. 考虑电力系统不确定性的机组检修计划安排[J]. 水电能源科学, 2011,29 (5): 152-155. SU Yun, ZHU Yaoming, ZHANG Jietan, et al. Generator maintenance scheduling model considering uncertainty of power system[J]. Water Resources and Power, 2011,29 (5): 152-155.

[3] 吴耀武, 邴焕帅, 娄素华. 含风电场的电力系统中考虑调峰压力平衡的机组检修规划模型[J]. 电网技术, 2012, 36(11): 94-100. WU Yaowu, BING Huanshuai, LOU Suhua. A unit maintenance scheduling model considering peak regulation pressure balance for power system containing wind farms [J]. Power System Technology, 2012, 36(11): 94-100.

[4] 李伟, 张宏图, 王群锋, 等. 吉林省风电规律特性及减少弃风政策建议研究[J]. 可再生能源, 2013,31 (2): 123-126. LI Wei, ZHANG Hongtu, WANG Qunfeng, et al. Characteristics of wind power in Jilin province and the study of wind curtailment reduction policy recommendations[J]. Renewable Energy Resources, 2013,31 (2): 123-126.

[5] 王海彪, 郭瑞鹏, 姜忠民, 等. 考虑大规模风电接入的发电机组检修计划最小失负荷期望模型[J]. 电力系统保护与控制, 2013, 41(4): 26-32. WANG Haibiao, GUO Ruipeng, JIANG Zhongmin, et al. Generation maintenance scheduling based on minimum loss of load expectation considering significant wind power penetration[J]. Power System Protection and Control, 2013, 41(4): 26-32.

[6] 方陈, 夏清, 孙欣. 考虑大规模风电接入的发电机组检修计划[J]. 电力系统自动化, 2010, 34(19): 20-24. FANG Chen, XIAQing, SUN Xin. Generation maintenance scheduling with significant wind power penetration[J]. Automation of Electric Power Systems, 2010, 34(19): 20-24.

[7] 宋曙光. 风电功率波动特性及其与储能协调策略的研究[D]. 济南:山东大学, 2011. SONG Shuguang. Research on wind power fluctuation profile and its energy storage coordination strategy[D]. Jinan: Shandong University, 2011.

[8] 张宏宇. 考虑调峰因素的风电规划研究[D]. 北京:中国电力科学研究院, 2013. ZHANG Hongyu. Research on wind power planning considering peak regulation[D]. Beijing: China Electric Power Research Institute, 2013.

[9] 王洪涛, 刘旭, 陈之栩, 等. 低碳背景下基于改进通用生成函数法的随机生产模拟[J]. 电网技术, 2013, 37(3): 597-603. WANG Hongtao, LIU Xu, CHEN Zhixu, et al. Power system probabilistic production simulation based on improved universal generating function methods in low-carbon context [J]. Power System Technology, 2013, 37(3): 597-603.

[10] 刘旭. 含风电场的随机生产模拟[D]. 济南:山东大学, 2013. LIU Xu. Probabilistic production simulation with wind farm[D]. Jinan: Shandong University, 2013.

[11] 周玮, 彭昱, 孙辉, 等. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(25): 13-18. ZHOU Wei, PENG Yu, SUN Hui, et al. Dynamic economic dispatch in wind power integrated system[J]. Proceedings of the CSEE, 2009, 29(25): 13-18.

[12] 张节潭, 王茂春, 徐有蕊, 等. 采用最小累积风险度法的含风电场电力系统发电机组检修计划[J]. 电网技术, 2011,35(5): 97-102. ZHANG Jietan, WANG Maochun, XU Yourui, et al. Generation unit maintenance scheduling based on minimum cumulative risk algorithm for power system containing wind farms[J]. Power System Technology, 2011,35 (5): 97-102.

(责任编辑 侯世春)

Research on generation maintenance scheduling considering wind power

LEI Yu

(No.71496 Unit, Yantai 265800, China)

In order to solve the problem, the wind curtailment problem, which was brought by the grid-connection of large-scale wind power system, this paper combined principal component analysis (PCA) with hierarchical cluster analysis to obtain the typical models of wind power output in four seasons, established the UGF model for wind power output by apportionment in average and the decision model of generator maintenance scheduling plan optimization considering the seasonal characteristics of wind power. Taking minimum wind curtailment and minimum maintenance cost in all maintenance time intervals as optimization objective, the paper solved the model by particle swarm optimization algorithm. The practical example verifies that the model, which is feasible and effective, succeeds in enhancing the capacity of wind power and in reducing wind curtailment when generation maintenance scheduling decision considering the seasonal characteristics of wind power is made.

seasonal characteristics of wind power; unit maintenance scheduling; universal generating function; particle swarm optimization algorithm

2015-12-02。

雷 宇(1986—),男,硕士,研究方向为电力系统调度自动化、电力系统运行与控制。

TM614

A

2095-6843(2016)02-0145-05