夏季短期电力负荷ARIMA-SVR组合预测模型

王喜平,王雅琪

(华北电力大学 经济管理系,河北 保定 071003)



夏季短期电力负荷ARIMA-SVR组合预测模型

王喜平,王雅琪

(华北电力大学 经济管理系,河北 保定 071003)

针对夏季电力负荷因波动性、非线性等特点和易受气温、日类型等因素影响,用单一模型难对其做出精确预测的问题,基于自回归积分滑动平均模型(ARIMA)和支持向量回归机模型(SVR)的优点,构建了ARIMA-SVR组合预测模型。通过ARIMA预测模型进行线性拟合,然后根据粒子群算法(PSO)优化参数的SVR预测模型对ARIMA模型的残差预测值进行修正。结合实际案例对夏季用电负荷进行趋势预测和误差分析,结果表明ARIMA-SVR组合模型的负荷预测精度较高,优于传统的单一预测模型。

支持向量回归机;自回归积分滑动平均模型;粒子群优化;短期负荷预测;误差分析

电力系统短期负荷预测是电网管理和调度的重要内容,可有效降低发电调度成本,确保电网安全、稳定运行。国内外学者提出了各种负荷预测方法,大致可分为两大类:一类是传统的预测方法,如指数平滑模型(Exponential Smoothing,ES)、自回归滑动平均模型(Autoregressive Moving Average,ARMA)、自回归积分滑动平均模型(Autoregressive Integrated Moving Average,ARIMA)等[1-2],这些方法算法简单、运算快速,但是由于这些模型都为线性模型,在电力负荷预测应用中只能考虑负荷的历史发展趋势,无法引入温度、类型日等对负荷有敏感影响的因素,因此对于复杂的非线性电力负荷预测具有一定的局限性,预测精度难以提高;另一类是现代智能预测算法,如人工神经网络(Artificial Neural Network,ANN)和支持向量回归(Support Vector Regression,SVR)等[3],但ANN在对数据的预测过程中也存在网络结构难以科学确定、收敛速度较慢以及容易陷入局部极小等缺陷。SVR因具有泛化性能强、拟合精度高、计算速度快、全局最优等显著优势,所以,已成为预测电力负荷的一种重要的工具[4]。通过研究发现,SVR中各特征参数对其泛化性和预测精度有很大的影响,因此SVR模型的参数选择和优化成为负荷预测的重点研究内容。文献[5]提出支持向量机的粒子群优化算法的用电量预测方法,选取较优的支持向量机训练参数组合,证明了该方法的电力负荷预测精确度高于神经网络;文献[6]利用最小二乘支持向量机确定特征参数,对ARIMA预测误差进行修正,并对哈尔滨电网负荷进行了实例预测。随着预测模型研究的不断深入,很难用单一模型来描述和预测电力负荷所有变化特性及影响因素,因此结合各种预测模型优点的组合方法越来越受到关注。文献[7]通过ARIMA-SVM组合模型对微电网进行短期负荷研究,充分利用了两种模型特有的优势,在一定程度上提高了负荷预测的精确性和实用性。

夏季电力负荷既呈现明显的周期性和波动性,又会受到天气、日类型等因素的影响,数据存在显著的不确定性结构[8]。因此,结合夏季电力负荷波动性和敏感性等特点,本文利用ARIMA和SVR算法建立电力负荷组合预测模型,通过粒子群优化算法(Particle Swarm Optimization, PSO)选择SVR模型最佳参数组合,不仅能避免单一预测算法存在的不足,还能大大提高预测的精确度。

1 相关理论模型

1.1 ARIMA模型

ARIMA模型是一种精确度较高的时间序列预测模型,由自回归模型(AR)和滑动平均模型(MA)组成。建模的基本思想是:将非平稳时间序列经过差分等方式进行序列变换,使得原序列平稳化,再通过观察自相关性、偏相关性和互相关系,以及严格的有效性检验,确定自回归模型阶数(p)、差分次数(d)和滑动平均模型阶数(q)这3个参数,进而对时间序列进行预测分析[9]。ARIMA(p,d,q)模型结构为:

Φp(B)dxt=θq(B)εt

E(εt)=0, var(εt)=σt2,E(εtεs)=0,s≠t

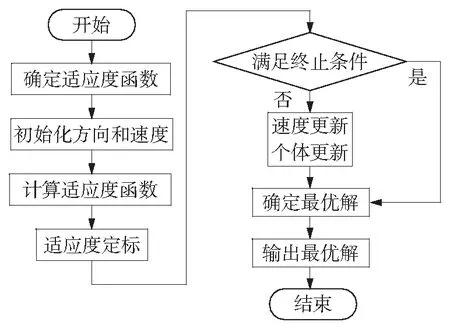
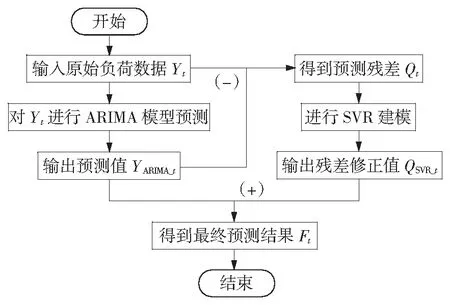
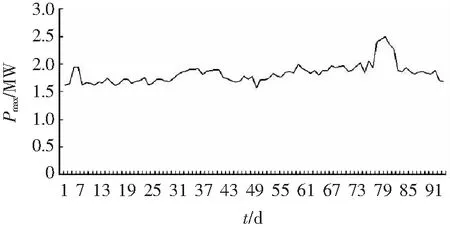
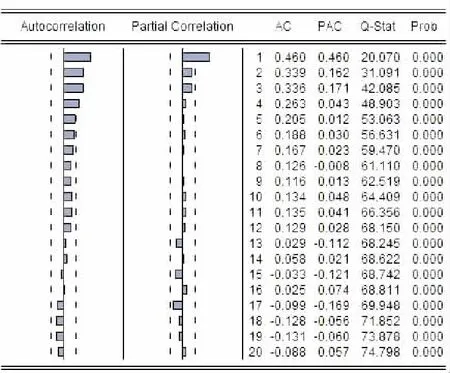
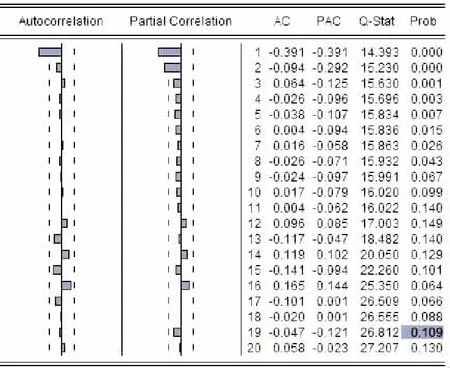
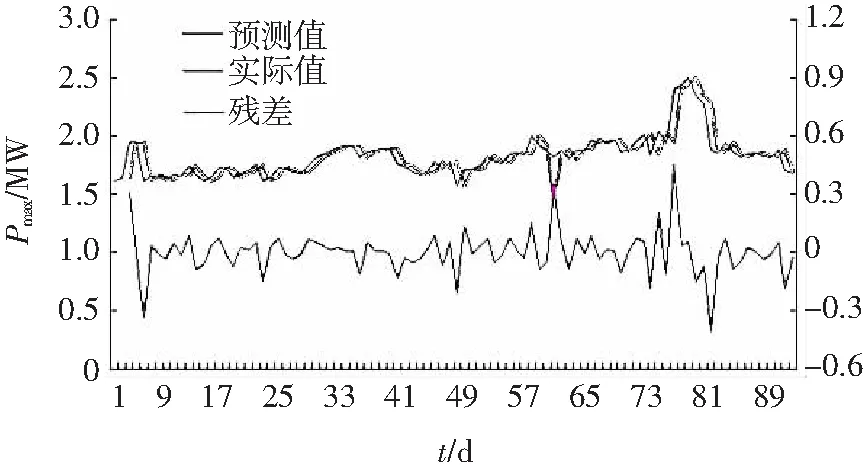
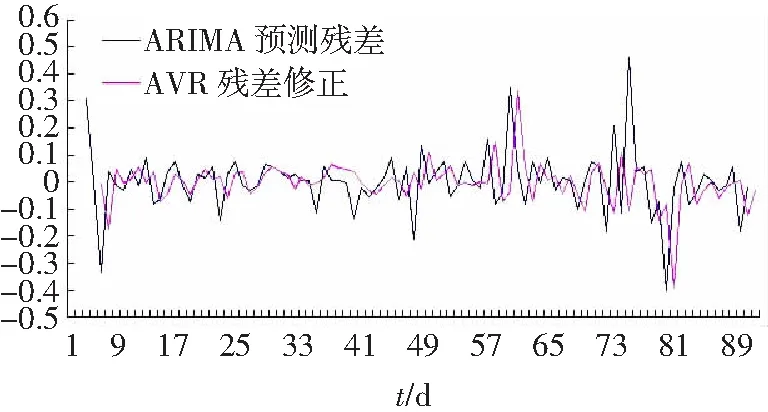
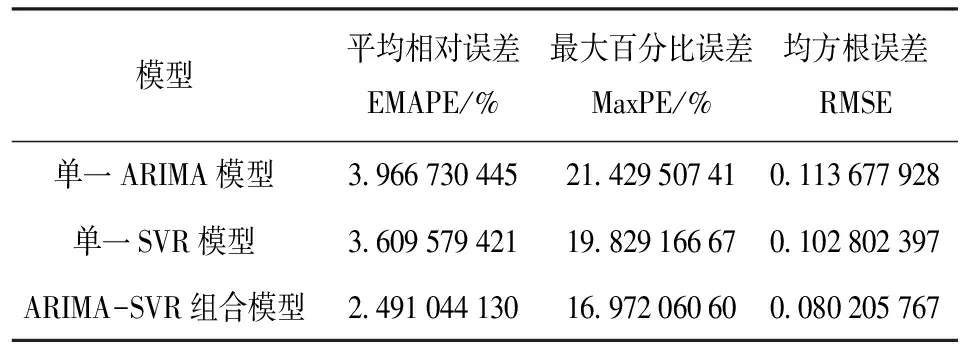
E(xsεt)=0,∀s

1.2 SVR模型

支持向量机(Support Vector Machine, SVM)是一种基于统计学VC维理论的智能算法。SVR作为SVM的一种，具有很好的泛化性、鲁棒性等,在小样本、非线性以及高维模式识别中表现出了特有的优势[10]。其建模的基本思想是:通过非线性转换将输入变量转换到一个高维空间,在该空间中求取最优线性超面,并将寻找最优线性超平面的算法归结为求解一个二次规划问题[11]。

设有一组训练样本集(xi,yi),其中,i=1,2,…,n;xi∈Rn为输入变量,yi∈R,为对应的输出值,则SVR的估计函数为

f(x)=ωφ(x)+b,φ:Rn→F,ω∈F

式中:ω为权重向量,φ(x)为非线性映射,b为位移偏置。

根据统计学理论的结构风险最小化准则,SVR通过最小化结构风险函数来确定回归函数,即

引入正向松弛变量ζi和ζi*,所以SVR算法可以表示为

式中,核函数K(xi,xj)=φ(xi)·φ(xj),它使SVR具有更强的非线性预测能力。

最终,可得到支持向量机回归估计函数为

1.3 PSO算法参数寻优

粒子群优化算法(Particle Swarm Optimization,PSO)是计算智能领域一种新兴的优化算法,基本思想源于对人工生命和鸟类捕食行为的研究[12]。每个粒子都采用方向和速度两个量来确定在空间中的位置,不同粒子具有对应于与目标函数相关的个体适应度。每个粒子根据自身的飞行经验和群体的飞行经验来调整自己的位置,向最优点靠拢。利用PSO对SVR进行参数优化的整体算法过程如图1所示。

图1 利用PSO优化SVR参数的算法流程图

2 组合模型建模流程

组合模型具体步骤如图2所示。

图2 ARIMA-SVR组合模型预测流程图

步骤1:确定原始电力负荷数据Yt,构建电力系统负荷数据时间序列,利用差分法对非平稳时间序列进行平稳化处理,通过分析时间序列的自相关性、偏相关性和互相关系,为ARIMA预测模型进行初步定阶,通过检验确定最优预测模型并进行负荷预测,得到预测值YARIMA_t。

步骤2:通过ARIMA预测模型得到电力负荷实际值与预测值在t时的残差,即

Qt=Yt-YARIMA_t

步骤3:对得到的残差Qt进行SVR建模,并引入气温、周末和法定节日3个变量,从而确定模型的输入变量包括t时的残差(Qt)、最高气温(Tmax)、最低气温(Tmin)、是否周末(W)和是否节日(H)。通过SVR预测模型,得到残差的修正值QSVR_t。

步骤4:将ARIMA模型预测值YARIMA_t与SVR模型残差修正值QSVR_t相加,得到最终组合模型的预测值Ft,即

Ft=YARIMA_t+QSVR_t

3 实例分析

3.1 数据来源与内容

选取河北省邯郸市新世纪商业广场2013年6月—8月每日的历史最大负荷数据作为样本进行研究。该研究引入“最高气温、最低气温、是否周末和是否节日”作为输入变量,建立组合模型。92 d的最大负荷数据如图3所示。

图3 新世纪商业广场2013年6—8月每日最大负荷

3.2 模型预测

3.2.1 ARIMA建模

通过观察新世纪2013年6月—8月负荷数据时间序列的自相关性和偏相关性,并对时间序列进行一阶差分,如图4和图5所示。

图4 原序列自相关和偏自相关图

图5 一阶差分序列的自相关和偏自相关图

对模型进行检验后,最终确定ARIMA(1,1,2)模型为最优预测模型。ARIMA(1,1,2)模型电力负荷预测结果如图6所示。

图6 ARIMA(1,1,2)模型预测结果

3.2.2 SVR建模

观察图6中ARIMA模型的92个残差数据波动趋势,选取第1～91个残差数据及当日最高气温、最低气温、是否周末和是否节日作为输入变量,选取第2～92个残差数据作为输出变量,通过PSO优化获得SVR残差修正最优参数模型,得到惩罚参数C为1,核函数参数为1.414 21。SVR模型残差修正结果如图7所示。

图7 SVR模型残差预测结果

将ARIMA模型预测值与SVR模型残差修正结果相加,得到最终的ARIMA-SVR组合模型的预测结果,如图8所示。

图8 ARIMA-SVR组合模型预测结果

3.2.3 预测结果分析与比较

为了进一步验证ARIMA-SVR组合模型的准确性和有效性,将其预测结果与单一SVR算法和单一ARIMA方法的预测结果进行对比。三类模型的电力负荷预测结果如图9所示。

图9 三类模型预测效果比较

由图9可以看出,本文所建立的ARIMA-SVR组合模型具有很好的预测效果,而单一模型的预测效果误差较大。采用平均相对误差(EMAPE)、最大百分比误差(MaxPE)和均方根误差(RMSE)比较分析三类模型,其具体预测效果比较如表1所示。

表1 组合模型预测效果比较

由表1可以看出,在这三类模型中,ARIMA-SVR组合模型的各项指标都比单一模型要小,说明该组合模型的预测效果要比单一方法要好。

4 结 语

在ARIMA模型和利用PSO优化参数SVR模型的基础上,提出了ARIMA-SVR短期电力负荷预测组合模型,并结合夏季每日的历史最大负荷数据,以气温、日类型作为输入的特征数据进行电力负荷预测,系统分析ARIMA-SVR对夏季短期负荷预测的实用性和可行性,并与单一模型预测进行对比。通过实例分析表明,基于ARIMA-SVR组合方法进行短期负荷预测的结果合理,有较高的预测精确度,是一种很有价值、实用性强的预测方法。

[1] 陈娟, 吉培荣, 卢丰. 指数平滑法及其在负荷预测中的应用[J]. 三峡大学学报(自然科学版), 2010, 32(3): 37-41. CHEN Juan, JI Peirong, LU Feng. Exponential smoothing method and its application to load forecasting [J]. Journal of China Three Gorges Universtiy (Natural Science), 2010，32(3)：37-41.

[2] 朱陶业, 晏小兵. ARIMA模型在广西短期电力负荷预测中的应用[J].长沙电力学院学报, 2000, 15(2): 20-22. ZHU Taoye, YAN Xiaobing. The ARIMA model in the forecasting of power load in Guangxi [J]. Journal of Changsha University of Electric Power, 2000, 15(2): 20-22.

[3] BO Jin, TANG Y C, ZHANG Yanqing. Support vector machines with genetic fuzzy feature transformation for bio-medical data classification [J]. Information Sciences, 2007, 177(2):476-489.

[4] VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer, 1995.

[5] 曾勍炜, 徐知海, 吴键. 基于粒子群优化和支持向量机的电力负荷预测[J]. 微电子学与计算机, 2011, 28(1): 147-153.ZENG Qingwei, XU Zhihai, WU Jian. Forecasting of electricity load based on particle swarm optimization and support vector machi-ne [J]. Microelectronics & Computer, 2011, 28(1): 147-153.

[6] 刘国徽, 刘小满, 余雪芳,等. 基于ARIMA和LS-SVM组合模型的短期负荷预测[J]. 广东电力, 2010, 23(11): 14-17. LIU Guohui, LIU Xiaoman, YU Xuefang, et al. Short-term load forecasting based on ARIMA-LS-SVM model [J]. Guangdong Electric Power, 2010, 23(11): 14-17.

[7] 王春友, 文闪闪, 秦跃进,等. 基于ARIMA-SVM模型的微电网短期负荷组合研究[J]. 陕西电力, 2014, 42(3): 19-23. WANG Chunyou, WEN Shanshan, QIN Yuejin, et al. Study on microgrid short-term load combination forecasting based on ARIMA-SVM model [J]. Shanxi Electric Power, 2014, 42(3): 19-23.

[8] 崔和瑞, 彭旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制, 2015, 34(4): 108-114. CUI Herui, PENG Xu. Summer short-term load forecasting based on ARIMAX model [J]. Power System Protection and Control, 2015, 34(4): 108-114.

[9] 刘亚, 张国忠, 何飞. 基于ARIMA模型和BP网络的电力负荷预测[J]. 湖北电力, 2003, 27(2): 13-15. LIU Ya, ZHANG Guozhong, HE Fei. Electric load forecasting based on ARIMA model and BP network [J]. Hubei Electric Power, 2003, 27(2): 13-15.

[10] ELATTAR E E, GOULERMAS J, WU Q H. Electric load forecasting based on locally weighted support vector regression[J]. IEEE Trans on Systems, Man and Cybernetics, 2010, 40(4): 438-447.

[11] 邱存勇, 肖建. 基于支持向量回归的电力系统短期负荷预测[J]. 计算机仿真, 2013, 30(11): 62-65. QIU Cunyong, XIAO Jian. Power system short-term load forecasting based on SVM [J]. Computer Simulation, 2013, 30(11): 62-65.

[12] 王义军, 李殿文, 高超, 等. 基于改进的PSO-SVM的短期电力负荷预测[J]. 电测与仪表, 2015, 53(3): 22-25 WANG Yijun, LI Dianwen, GAO Chao, et al. Short-term power load forecasting based on improved PSO-SVM [J]. Electrical Measurement & Instrumentation, 2015, 53(3): 22-25.

(责任编辑 郭金光)

Summer short-term load forecasting based on ARIMA-SVR combination model

WANG Xiping, WANG Yaqi

(Department of Economy and Management, North China Electric Power University, Baoding 071003, China)

Since summer short-term load has the characteristics of fluctuation and nonlinearity, easily affected by temperature, day type and other factors, it is difficult to get the accurate result, relying on single traditional forecasting model. This paper established the ARIMA-SVR combination forecasting model, based on the advantages of ARIMA and SVR, through which the data was linearly fitted. Then the error of ARIMA forecasting was corrected by the SVR forecasting model with the optimized parameters by particle swarm optimization. In the context of the practical cases, the combination forecasting model was used to forecast the trend and to analyze the errors of the summer short-term load. The experimental results indicate that the ARIMA-SVR combination model has higher prediction accuracy than the single model does, which also has a high application value in the forecasting of electricity load.

support vector regression; autoregressive integrated moving average; particle swarm optimization; short-term load forecasting; error analysis

2015-08-09。

王喜平(1969—)，女，副教授，研究方向为电力经济。

TM715

A

2095-6843(2016)02-0104-05