改进蚁群算法在配电网重构问题中的应用

王 晖,赵 亮,刘建树

(1.长春工程学院 电气与信息工程学院,长春 130012; 2.配电自动化工程研究中心,长春 130012; 3.国网吉林省电力有限公司,长春 130021; 4.国网四平供电公司,吉林 四平 136000)



改进蚁群算法在配电网重构问题中的应用

王 晖1,2,赵 亮3,刘建树4

(1.长春工程学院 电气与信息工程学院,长春 130012; 2.配电自动化工程研究中心,长春 130012; 3.国网吉林省电力有限公司,长春 130021; 4.国网四平供电公司,吉林 四平 136000)

针对配电网重构问题,提出了用一种基于方向信息素的改进蚁群算法来求解。该算法给出了新的信息素更新策略,并加入探索率因子的支路选择策略,从而加快蚁群算法的收敛速度和控制精度,防止算法陷入局部最优。通过仿真实验表明,基于方向性信息素的改进蚁群算法在配电网重构问题中能够进行有效的应用,且在求解问题时具有很快的收敛速度,同时能够求出较优的解。

配电网重构;改进蚁群算法;方向信息素

配电网的重构问题是通过变换配电线路中联络开关的开合来选择不同的供电电源,并将线路上的负荷进行转移,目的就是解除线路过载,减小网络上的功率损耗,提高输电质量等。由于配电网具有结构复杂、线路长、损耗比较大等特点,配电网重构问题通常看作是一个有着多个约束条件的复杂的组合优化问题。因此为了解决这一问题,国内外学者已做了大量的研究,方法主要包括数学优化方法、启发式方法和人工智能算法等这三类。采用数学优化方法时,有时会出现“组合爆炸”问题,所以用该方法解决问题时的计算时间很长,在实际应用上有一定的困难;启发式的方法主要包括最优流模式法[1]和支路交换法[2]两种,该方法在解决配电网重构问题时容易陷入局部解,难以保证全局最优;人工智能算法是近几年新发展起来的一种解决配电网重构的有效方法[3],目前应用于配电网重构问题的人工智能算法主要有遗传算法(genetic algorithm,GA)[4-6],模拟退火[7]禁忌搜索 (tabu search,TS)算法、粒子群优化[8-9](particle swarm optimization,PSO)算法等。其中蚁群算法也是人工智能算法的一种,近年也有很多研究者将该蚁群算法应用到解决配电网重构问题中,但相对于其他人工智能算法,蚁群算法在配电网重构中的应用还相对较少。因此本文提出用基于方向性信息素的蚁群算法(Ant Colony Optimization based on Directed Pheromone DPACO)来解决配电网重构问题,即对配电网重构的模型利用改进方向性信息素的蚁群算法进行解析,将重构问题中的约束条件代入求解,以减小配电网网损。仿真实验证明,基于方向性信息素的蚁群算法在解决配电网重构问题时能够取得较优的结果。

1 配电网重构问题

配电网重构问题选取以配电网网损最小为目标函数,以减小配电网网损为目的,配电网的网损主要包括变压器自身的铜耗和铁损以及线路上导线的损耗等,其目标函数为

(1)

式中:Nb为配电网中支路的数目;Ri为第i条支路上的电阻;Pi和Qi分别为线路支路i上的有功功率和无功功率;Ui为支路i末端的节点电压;ki为0、1离散变量,用来表示支路i开关的开合状态,0表示打开,1表示闭合；Ii为支路i上的电流。

在进行配电网重构时,需要满足如下约束条件:

1) 网络拓扑约束。配电网重构之后,所形成的网络必须是辐射状。

2) 供电约束。重构之后的配电网必须满足线路负荷要求,同时在配电网中不能够存在独立结点。

3) 不等式约束。包括节点电压约束支路过载约束、变压器过载约束等。

Uimin≤Ui≤Uimax

(2)

Si≤Simax

(3)

Ii≤Iimax

(4)

St≤Stmax

(5)

式中:Uimax和Uimin分别为节点i所允许的电压的上限值和下限值;Si和Simax分别为流过各支路i的功率的计算所得值及其最大容许的值;Ii和Iimax分别为流过支路i的电流及其最大容许电流值;St和Stmax分别为变压器的供出功率及其最大容许值。

2 基于方向性信息素的改进蚁群算法

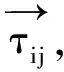
(6)

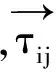
为防止传统蚁群算法过早的陷入局部最优,改进算法中,在进行路径选择时,加入一个探索率值ε,其值递减的计算表达式为

ε(t+n)=ε(t)-c

(7)

式中,c为一个常数。

蚂蚁每完成一次遍历,便对ε的值进行一次更新。

3 改进蚁群算法在配电网重构中的应用

3.1 利用蚁群算法构建最小生成树

根据配电网重构中网络拓扑约束和供电约束条件的要求,重构后的配电网必须要包含配电网络中的所有节点,同时要求所生成的解为辐射状,即没有回路,因此,可以使用蚁群算法对网络进行遍历,利用蚁群算法来构建最小生成树。设定Sk(t)为第k只蚂蚁在t时刻连入树的节点的集合,即对应蚁群算法中的禁忌表tabuk;Wk(t)为第k只蚂蚁在t时刻没有连入树的节点集合,即表示所有候选点的集合;Ek(t)为在t时刻在集合之间所有的可选路径的集合,表示当前状态下所有可行解的集合;Pk(t)为在t时刻各条路径上的状态转移概率值;Ak(t)为在t时刻可在集合Ek(t)中加入新的可选边的集合;s-w为从节点s到节点w的一条边,s和w分别为边的顶点。

用蚁群算法构建最小生成树的步骤为:

Step1:设置t=0,蚂蚁k从起点出发,Sk(0)={s0}。

Step2:蚂蚁k根据Pk(t) 从集合Ek(t)中选择边j(s-w)。

Step3:检查在集合Ek(t)中是否存在到节点w的边,若存在则断开j,返回Step2;否则执行Step4。

Step4:更新节点集合和Wk(t),将w节点从集合Wk(t)移到Sk(t),即Wk(t+1)=Wk(t)-{w},Sk(t+1)=Sk(t)+{w}。

Step5:检查集合Wk(t)是否为空,若为空,则表示所有的负荷节点已经被连入生成树,结束;否则执行Step6。

Step6:更新集合Ek(t),将边j从集合Ek(t)中移除,并将新的可选边集合Ak(t)加入到集合Ek(t)中,即Ek(t+1)=Ek(t)+Ak(t)-{j}。

3.2 信息素更新

3.2.1 普通信息素的更新

在配电网络中,初始时刻,初始化网络中各条线路上的信息素,设置τij=d,d为一常数。蚂蚁在完成一次遍历之后,即得到一棵最小生成树,生成一个辐射网络,并将得到的网络中的数据进行计算,若其满足约束条件，即可通过潮流计算得到此次迭代中所得路径的网损值flossi。在配电网络中,各条支路之间是有区别的,在进行路径选择时,必须考虑每条支路上的电阻值Rij。

蚂蚁k在完成一次遍历后,需按照式(8)和(9)对当前形成的网络中各条线路上的信息素更新。

τij(t+n)=(1-ρ)·τij(t)+Δτij(t)

(8)

(9)

式中:flossk为蚂蚁k在完成此次遍历之后所形成的辐射网络的网损值;Rij为节点i和j之间的线路上的电阻值;ρ为信息素的挥发度。

通过普通信息素的更新,可以对各条支路上的信息素进行控制,记录可行解所包含的路径,加快算法的求解速度。

3.2.2 方向性信息素的更新

在蚂蚁完成一次遍历之后,对所形成的辐射网络中的各支路上的方向性信息素进行更新。在进行网络中方向性信息素的更新时,选取本次迭代中所有蚂蚁形成的路径中具有最小网损值的一条进行更新[10]。

方向性信息素的更新规则为

(10)

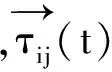
当本次迭代中,所有蚂蚁完成一次迭代之后,计算各蚂蚁所生成网络的网损值,对网损值最小的方案上的各支路信息素进行更新,更新时,判断当前待更新支路上的信息素值与所要更新的值进行比较,选取较大的值对此支路上的方向性信息素进行更新。

3.3 支路选择策略

蚂蚁在遍历过程中,计算当前各可选路径上的概率的计算表达式为

(11)

(12)

3.4 改进蚁群算法在配电网重构中的实现步骤

将基于方向信息素的改进蚁群算法在配电网重构问题中进行应用,其算法步骤为

Step1:读取配电网的各项数据值,作为算法的初始数据。

Step2:初始化配电网重构问题的环境信息。设置各个节点上的方向性信息素值为0,各条支路上的信息素值τij(t)=const,其中const表示一个较小的常数值；设置ε的初始值ε=N,N为一固定的整数值；设置最大迭代次数Ncmax；初始时刻Δτij(0)=0,将蚁群中各蚂蚁k的禁忌表tabuk置空,将m只蚂蚁随机放到n个配电网节点上,并将当前各蚂蚁所在的节点加入到其禁忌表中。

Step3:比较随机数与探索率的大小。产生一个在0到n之间的随机数,若随机数大于探索率则蚂蚁个体根据概率式(10)计算的概率从可选边集合Ek(t)中选择边j(假设改变为s-w),反之,则随机从可选边集合Ek(t)中选择一条边。

Step4:判断集合Ek(t)中,是否存在到节点w的边,若存在，则断开j,返回步骤(3);否则执行步骤Step5。

Step5:修改禁忌表。边选择完成之后,根据所选的边,将蚂蚁移动到新的节点,同时,将该节点移到该蚂蚁的禁忌表中。

Step6:判断是否完成遍历。判断集合Wk(t)是否为空,即网络中的节点是否遍历完成,若未遍历完,则执行Step7,否则跳转到Step8。

Step7:更新集合Ek(t),将边j从集合Ek(t)中移除,并将新的可选边集合Ak(t)加入到集合Ek(t),即Ek(t+1)=Ek(t)+Ak(t)-{j},跳转到Step3。

Step8:循环次数加1,根据式(7)更新探索率ε的值,计算各网损值。根据式(8)和式(9) 更新每个节点上的普通信息素值,找出各网损之中的最小值,根据式(10)更新方向性信息素值。

Step9:若满足结束条件,即达到最大循环次数Ncmax,则结束循环并输出计算结果,否则,将禁忌表清空并跳转到Step3。

4 实验仿真及运算结果分析

采用IEEE33节点配电系统作为分析算例,该算例在配电网重构前的节点结构如图1所示,其参数额定电压为12.66 kV、节点33个、支路37条、联络开关5个、总负荷为 3715 kW+j2300 kvar、功率基准10 MVA。

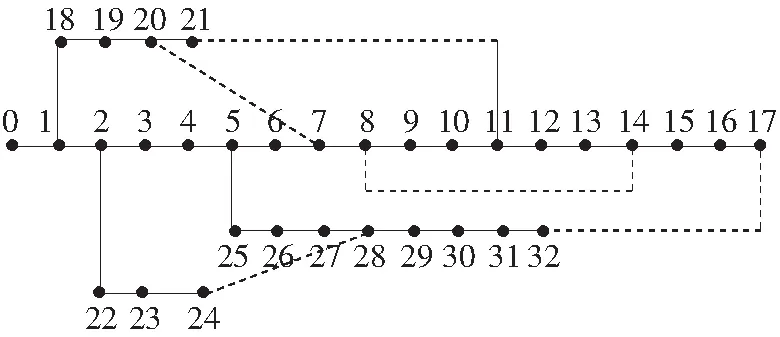
图1 IEEE33节点配电系统结构图

设置各参数为蚂蚁数目m=30,各路径上的初始信息素τ(0)=0.2,α=1,β=5,γ=25,ρ=0.6,ε=50,Q=1,Q′=10,然后进行仿真实验,实验结果如表1所示。

表1 实验计算结果

Table 1 Experimental results

由表1可见,与重构前相比,使用改进算法重构后的网络,网损值明显的降低了28%,对配电网性能的提高有很大的帮助。同时,与基本蚁群算法相比,使用改进后的蚁群算法进行重构时网损值也较小。随着蚂蚁迭代次数的增加,基本蚁群算法和改进的蚁群算法在计算网损值时的收敛情况,如图2所示。

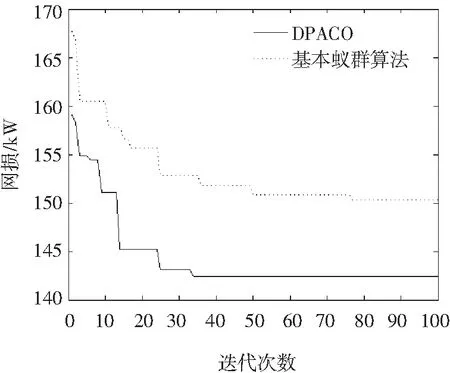
图2 DPACO与基本蚁群算法网损收敛对比图

从图2中可以看出,改进算法在进行到33次左右的时候,就能够达到收敛,与利用基本蚁群算法求解重构问题相比,不仅收敛速度较快,而且达到收敛时的网损值也较小。由此表明,基于方向性信息素的改进蚁群算法在解决配电网重构问题时，能够在保证电能质量的情况下,有效地降低网损值,收敛速度也较快。

5 结 语

通过仿真结果对比分析可知,在解决配电网重构问题时,本文提出基于方向性信息素的改进蚁群算法较传统的蚁群算法收敛速度快,且切实可行。

[1] DARIUSH SHIRMOHAMMADI,H.WAYNE HONE. Reconfiguration of electric distribution networks for resistive line losses reduction. IEEE Trans On Power Delivery[J].1989,4(2):1492-1498.

[2] CIVANLAR S,GRAINGER J J,YIN H,et al. Distribution feeder reconfiguration for loss reduction. IEEE Trans On Power Delivery[J]. 1988,3(3):1217-1223.

[3] 王凌. 智能优化算法及其应用[M].北京:清华大学出版社,2001. WANG Ling. Intelligent optimization algorithm and its application[M]. Beijing: Tsinghua University Press, 2001.

[4] 赵金亮. 基于自适应遗传算法和蚁群算法融合的配电网重构[D].兰州理工大学,2011. ZHAO Jinliang. Distribution network reconfiguration based on the combination of adaptive genetic algorithm and ant colony algorithm[D]. Lanzhou University of Technology, 2011.

[5] ZHU J Z. Optimal reconfiguration of electrical distribution network using the refined genetic algorithm[J]. Electric Power Systems Research, 2002(62):37-42.

[6] 夏媚珠. 基于改进遗传算法配电网络重构的研究[D].广西大学,2004. XIA Meizhu. Research on distribution network reconfiguration based on improved genetic algorithm[D]. Guangxi University, 2004.

[7] 胡敏佑,陈元. 配电系统最优网络重构的模拟退火算法[J]. 电力系统自动化,1994,18(2):24-28. HU Minyou, CHEN Yuan. Simulated annealing algorithm of optimal distribution network reconfiguration[J]. Automation of Electric Power Systems, 1994,18(2):24-28.

[8] 陈根军,李继洗,唐国庆.基于Tabu搜索的配电网络重构算法[J].中国电机工程学报,2002,22(10):28-33. CHEN Genjun, LI Jixi, TANG Guoqing. A Tabu search approach to distribution network reconfiguration for loss reduction[J]. Proceedings of the CSEE, 2002,22(10):28-33.

[9] 靳晓凌,赵建国. 基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J]. 电网技术,2005,29(23):40-43. JIN Xiaoling, ZHAO Jianguo. Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization [J]. Power System Technology, 2005,29(23):40-43.

[10] 孟祥萍,片兆宇. 基于方向信息素协调的蚁群算法[J].控制与决策,2013,28(5):782-786. MENG Xiangping, PIAN Zhaoyu. Ant algorithm based on direction coordinating[J]. Control and Decision, 2013,28(5):782-786.

(责任编辑 郭金光)

Application of improved ant colony algorithm in distribution network reconfiguration

WANG Hui1,2, ZHAO Liang3, LIU Jianshu4

(1.School of Electrical Engineering and Information Technology, Changchun Institute of Technology, Changchun 130012, China;2.Distribution Automation Engineering Research Center, Changchun 130012, China; 3.State Grid Jilin Electric Power Co., Ltd.,Changchun 130021, China; 4.State Grid Siping Power Supply Company, Siping 136000, China)

To solve the problem of distribution network reconfiguration, an improved ant colony algorithm was proposed. It is an algorithm that has a new pheromone updating strategy and slip selection strategy with the factor exploration rate, which promote convergence speed and control accuracy of ant colony algorithm and prevent the algorithm from falling into local optimum. The simulation results show that the improved ant colony is applied effectively with fast convergence rate and is able to obtain optimum solution to solve the problem of distribution network reconfiguration.

distribution network reconfiguration; improved ant colony algorithm; directional pheromones

2015-11-23。

吉林省科技厅项目(20150203002SF);吉林省教育厅项目(2014339和2014309);长春市科技局项目(14KG026)和长春工程学院青年基本项目(320140002)。

王 晖(1984—),女,实验师，研究方向为智能优化算法在电力系统中的研究与应用。

TM723

A

2095-6843(2016)02-0100-04