基于博弈论的铁路工程投标报价策略研究

许晓伟，段晓晨，何长春

Xu Xiao-wei1，Duan Xiao-Chen1，He Chang-chun2

（1.石家庄铁道大学经济管理学院，河北石家庄050043；2.中铁二十局集团有限公司，陕西西安710016）

(1.School of Economics Management，Shijiazhuang Tiedao University，Shijiazhuang 050043, Hebei, China；2.China Railway twenty Bureau Group Co.Ltd.，Xi’an 710016，Shaanxi, China)

基于博弈论的铁路工程投标报价策略研究

许晓伟1，段晓晨1，何长春2

Xu Xiao-wei1，Duan Xiao-Chen1，He Chang-chun2

（1.石家庄铁道大学经济管理学院，河北石家庄050043；2.中铁二十局集团有限公司，陕西西安710016）

(1.School of Economics Management，Shijiazhuang Tiedao University，Shijiazhuang 050043, Hebei, China；2.China Railway twenty Bureau Group Co.Ltd.，Xi’an 710016，Shaanxi, China)

投标报价作为施工企业竞标的关键因素，对于中标结果起着重要的作用，而且还关系到企业中标后的利润。从投标人的角度出发，运用SWOT-CLPV分析法对投标前施工企业及竞争对手进行定性分析，根据企业投标态势采取相应策略。在此基础上，依据当前铁路工程评标时采用的综合评估法，利用博弈论建立投标报价博弈模型，经过推导得出施工企业的最优投标报价区间，并通过实例验证模型的适用性及科学性，为施工企业投标报价提供依据。

铁路工程；投标报价；综合评估法；SWOT-CLPV分析；博弈论

铁路工程作为我国的基础交通设施产业，是我国国民经济发展的重要组成部分。2015年，国家“十三五”规划中明确提出铁路工程建设在未来的一段时间内仍将是国家投资的重点，这也为铁路施工企业带来了良好的发展机会。铁路施工企业必须通过招投标的方式获取工程的承包权，在投标报价过程中选择最优的投标报价策略，是投标企业成功中标需要解决的问题[1]。在铁路工程投标报价过程中，施工企业为了增加中标机会，往往需要分析企业当前的投标态势，根据竞争对手的行为采取应对措施，这个过程可以看作是与竞争对手的博弈行为。为此，采用 SWOT-CLPV 分析法与博弈论相结合对投标报价策略进行建模分析。

1 投标报价模型构建

铁路施工项目投标报价决策是指铁路施工企业利用报价模型及自身的经验，经过一系列的计算、评估和分析，确定既能中标又能盈利的最优报价策略[2]。对于施工企业而言，铁路工程投标报价是一个博弈的过程，在进行投标报价之前需要了解竞争对手的情况，从而根据竞争对手的行为采取应对策略，最终确定投标报价。因此，首先，可以从铁路施工企业的业绩、资质、地域方面进行大致分析，确定竞争对手；其次，利用 SWOT-CLPV 分析法进行分析，根据分析结果选择铁路工程报价采用的策略；第三，依据采取的报价策略通过博弈论确定最优投标报价。

1.1 竞争对手 SWOT-CLPV 分析

SWOT 分析法是将企业的内部环境和外部环境相结合，对企业当前的态势进行分析并提出相应策略的一种分析模型[3]。改进的 SWOT 分析法即SWOT-CLPV， SWOT-CLPV 分析法建立在SWOT 的理论基础之上，可以定量分析施工企业的优势、劣势、机会、威胁相互作用转化关系，更加清晰地反映真实情况，做出有力的应对策略。SWOT-CLPV 分析法示意如表 1 所示。

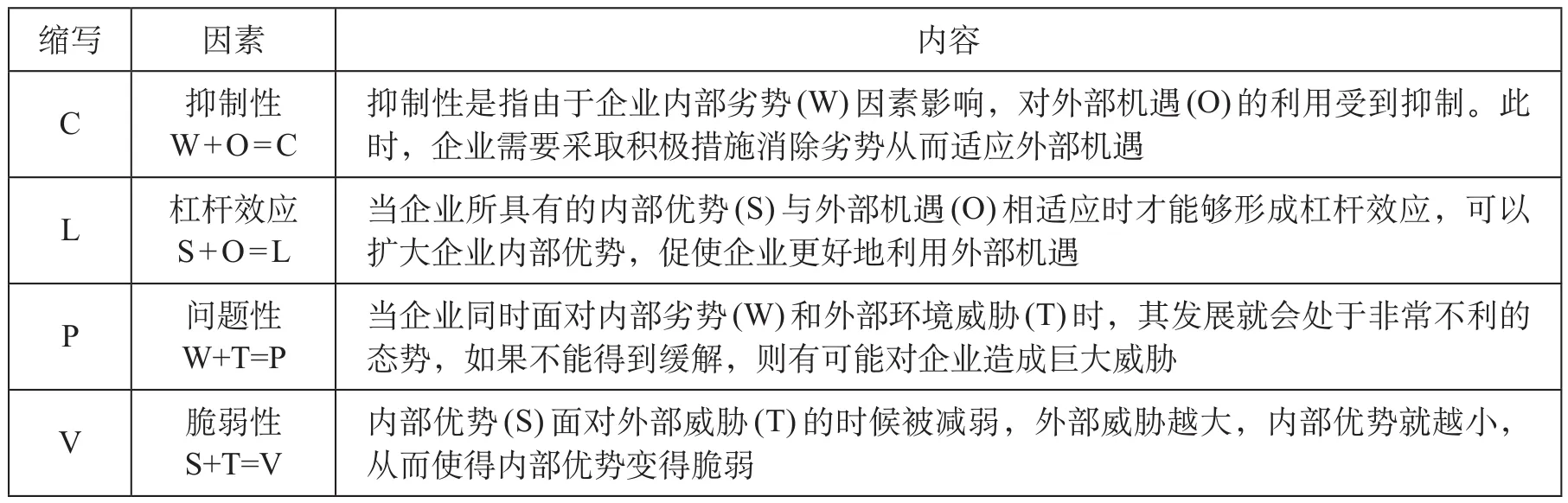
表 1 SWOT-CLPV 分析法示意

依据 SWOT-CLPV 分析结果，可以选择铁路工程报价策略。当前铁路工程报价采用的策略主要包括以下几种：①生存型报价策略。如果投标人当下面临的是生死存亡的危急关头，这时可以采取生存型报价策略。此时，投标人投标报价的目的不是为了赢取丰厚的利润，而是以企业生存为重，抱着即使不盈利也要夺标的态度来参与竞标，即报最低价，力争夺标。②竞争型报价策略。如果投标人希望通过竞标来继续开拓企业的市场占有率，以低盈利为目的，实际上就是通过竞争的手段，在成本精确计算的前提下，在极大范围内抢占市场，此时投标人可以选取竞争型报价策略。③盈利型报价策略。这种策略指在编制报价时可以充分利用本企业优势，并且以达到利润最大化为目的[4]。

1.2 综合评估法投标报价博弈模型

博弈论又称对策论，ROBERT J 认为博弈论是研究互动决策的理论[5]。在招投标过程中，由于参与投标的投标人在投标过程中无法知道其他投标人在投标时采取了什么行动，因此，依据博弈的分类可以将投标人与竞争对手之间的博弈行为看作是不完全信息静态博弈[6]。

1.2.1 综合评估法下的铁路评标标准及评分规则

依据中国铁路总公司相关文件的规定，铁路工程选用综合评估法进行评标时，评标基准价[7]如下。

式中：Z 为评标基准价；B 为招标人公布的标段最高投标限价；Di为第 i 个投标人的有效报价；Dmax为有效报价最高的投标人报价；Dmin为有效报价最低的投标人报价；n 为本标段有效报价投标人总数；K 为调整系数，从 0.98，0.985，0.99，0.995，1.0 中现场随机抽取。

将投标人的报价与经过计算得到的评标基准价进行比较，差值在 0～0.3% 之间的给予满分，否则将予以扣分。其中报价高于评标基准价的，每超过0.5% 扣 20 分；报价低于评标基准价 0.3% 的，每低于 1% 扣 10 分。

对于招标项目的最高投标限价 B，招标人应依据工程项目实际状况，在不超过施工图预算 (不含甲供物资设备) 的情况下，自主确定最高投标限价。

1.2.2 综合评估法投标报价博弈模型构建

（1）模型假设。①在博弈中，假设投标人一方作为局中人Ⅰ，其余的所有有效投标人为局中人Ⅱ。②假设投标人具有充分的铁路工程招投标领域的经验，对项目所在地的市场及项目状况比较了解，并且各投标人均为理性投标人。③假设在评标过程中存在投标人经评审后能够获得满分的情况。④基于研究内容，博弈过程中只考虑报价高低因素的影响，不考虑技术标的影响。

（2）博弈的基本要素。①参与人：参加投标的所有有效投标人，记为 i (i = 1，2，...，n)。②信息：在投标活动中，能够搜集到的有关业主和潜在竞争者的所有信息。③行动：对于投标人 i 而言，其行为就是其报价 Di。④策略：投标人根据自身实际状况及竞争对手的竞争状况所作出的报价即为所采取的策略，针对每一个投标人而言，其所作出的报价都有一定的浮动空间。⑤博弈规则：即选用综合评估法进行评标时所规定的扣分规则。⑥支付函数：由于只研究报价标部分，因而投标人最终获得的得分即为其收益。

（3）扣分公式。

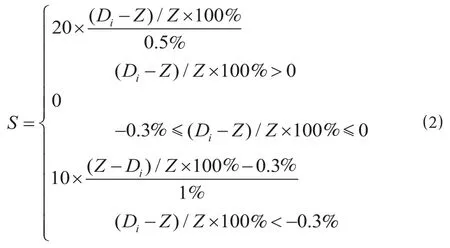
（4）博弈原则。博弈原则即得益最大原则。局中人Ⅰ的目的是力求竞标成功的同时又能够达到自身预期收益最大化。因此，在采取综合评估法进行评标时，投标人进行报价决策的原则就是在扣分最少的前提下，尽可能地提高报价，以此增加中标后的收益。

（5）满分报价区间。由上述分析可得，要想中标就必须扣分最少，使报价尽可能地接近或者最好落在满分报价区间上[8]。由公式 ⑵ 得当投标报价 Di满足公式 ⑶ 时达到最优。

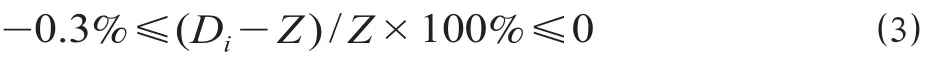
将计算评标基准价的公式 ⑴ 代入公式 ⑶，经过推导可以求出满分报价区间。但是，由上述分析可知，评标基准价的求取需要在所有投标人的有效报价中舍去一个最大值和一个最小值，以剩余 n-2 个有效投标报价的均值作为计算的基础。因此，对于满分报价区间需要分情况讨论。

①如果投标人 i 的报价 Di既不是 Dmax也不是Dmin，即可以看作投标人采取竞争型报价策略时的满分报价区间为

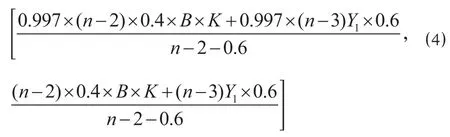
式中：Y1代表局中人Ⅱ去掉最高报价和最低报价之后的有效报价平均值。

②如果投标人 i 的报价 Di为 Dmax，即可以看作投标人采取盈利型报价策略时的满分报价区间为

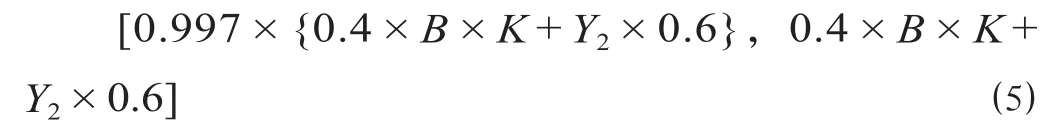
式中：Y2代表当局中人Ⅰ的报价为最高报价时，局中人Ⅱ去掉最低报价之后的有效报价平均值。

③如果投标人 i 的报价 Di为 Dmin，即可以看作投标人采取生存型报价策略时的满分报价区间为

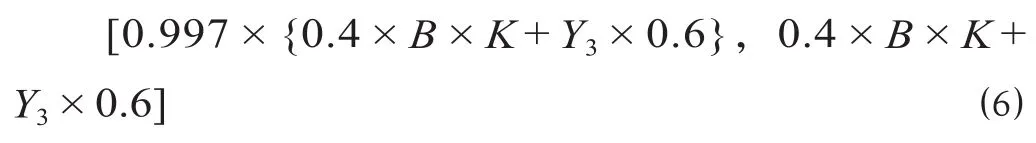
式中：Y3代表当局中人Ⅰ的报价为最低报价时，局中人Ⅱ去掉最高报价之后的有效报价平均值。

（6）关于 Y1，Y2，Y33 个有效报价平均值。在综合分析大量开标实例及研究文献之后，发现某一施工企业的报价水平在一段时间内是稳定的。因此，对于竞争对手的投标报价，可以利用指数平滑法来进行预测，做法如下。

式中：Γj为投标人第 j 次投标报价与最优报价的偏差系数；Dj为投标人第 j 次投标报价；Zj为投标人第 j 次报价中的最优报价。

式中：Γ′ 为投标人之前每次报价与最优报价的相对平均偏差系数。

式中：Γ″ 为投标人距离本次竞标最近的一次报价与最优报价的相对偏差系数；D″ 为投标人最近一次投标报价；Z″ 为在投标人最近一次报价中的最优报价。

式中：Γ为此次投标人报价和最优报价之间的偏差系数；α 为平滑系数，是一经验数值，当 α 取值大时，表示最近一次报价偏差的倾向性变动影响小，否则表示近期数值的倾向性变动影响大，建议 α 取值为 0.5～0.7。

则第 i 人的投标报价为

2 实例分析

XX 铁路项目招标人为某铁路客运专线有限责任公司，本段新建正线包括 2 座特大桥，桥梁的长度分别为 13.27 km 和 27.84 km，正线路基长度为4.924 km。该标段要求投标人需要具备公路、铁路、水利水电、港口与航道、市政公用工程、矿山工程施工总承包特级资质之一。该项目评标办法采用综合评估法，在招标文件中给出此次项目的最高投标限价为 326 438.38 万元。

2.1 施工企业与竞争对手 SWOT-CLPV 分析

中铁 X 局根据多年经验积累及资料的搜集，对潜在投标竞争对手的业绩、施工分布地域状况进行分析，初步确定中铁 A 局、中铁 B 局和中铁 C 局3 家公司为此次竞标项目中最具竞争力的对手。此外，中铁 D 局、中铁 E 局也为潜在的竞争对手。

以下结合企业自身状况及竞争对手情况对中铁X 局进行投标态势分析。

（1）企业优势 (S)：①资质资历优势；②资源丰富；③业绩优势；④施工技术水平先进；⑤组织管理水平高；⑥工程项目不饱和；⑦社会协调能力强。

（2）企业劣势 (W)：①融资能力有待进一步提升；②投标管理能力有待提高；③不注重投标策略应用；④过分注重投标价格；⑤主营施工业务造成利润偏低。

（3）外部环境机会 (O)：①企业社会信誉好；②铁路建设市场前景良好；③铁路建设项目进入障碍较高；④招投标市场体制日益规范。

（4）外部环境威胁 (T)：①竞争激烈；②接受企业联盟投标；③潜在的不正当投标行为；④铁路施工盈利水平低；⑤地域分布状况。

将中铁 X 局具有的内部优势、劣势与外部环境中的机遇组合，“S-O”“W-O”组合态势如表 2 所示。将中铁 X 局具有的内部优势、劣势与外部环境中的威胁组合，“S-T”“W-T”组合态势如表 3 所示。

分析表 2 中施工企业的 7 个优势与外界环境 4个机会的相互作用，可以看出中铁 X 局当前优势与机会能够形成较好的杠杆效应，机会对于绝大部分优势可以起到扩大作用。而企业劣势对于外部机会的抑制性较弱。即此次投标优势与机会的效应远大于劣势。但是，相对而言劣势 2 与劣势 3 抑制性比较明显，均为“2C”，因而企业应加强投标管理能力，并且在投标过程中注意投标策略的应用，为中标打下良好基础。由表 3 可以看出，企业的内部优势在受到外部环境威胁的影响下变得比较脆弱，最大的威胁来自于威胁 1、威胁 2、威胁 3，均为“6V”。而且当企业的内部劣势和外在威胁共同起作用时，会对企业的竞标结果产生极为不利的影响。

表 2 “S-O”“W-O”组合态势

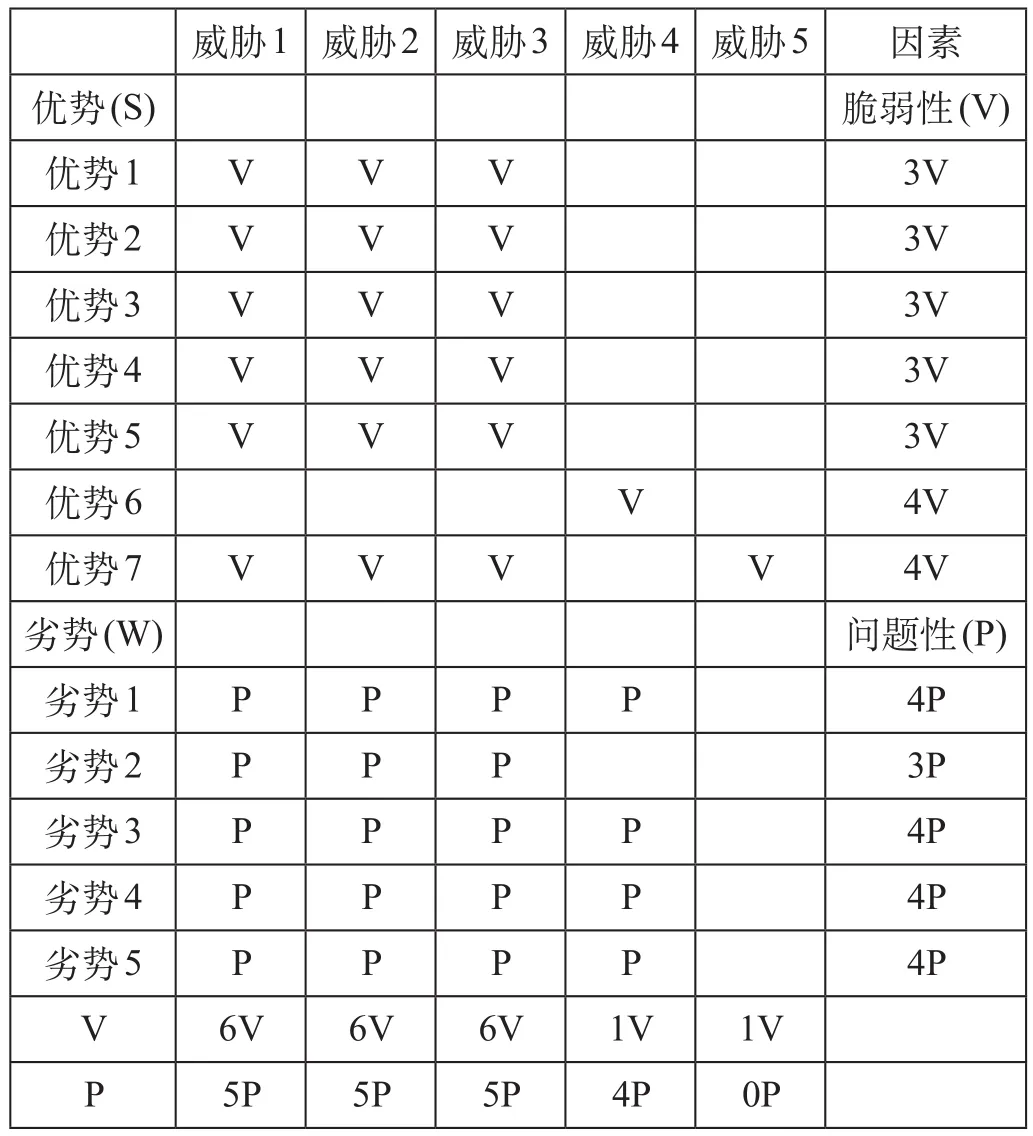
表 3 “S-T”“W-T”组合态势

通过 4 种因素的相互作用分析，可以看出，虽然企业的劣势对于机会的抑制性较小，机会对于优势有很好的扩大作用，但劣势和外部环境产生的问题性严重，优势面对外部威胁时比较脆弱。因此，企业面对这种情况，在博弈过程中结合综合评估法的博弈特征，适宜采取竞争型报价策略，在企业内部积极消除劣势因素，充分利用优势因素及外部机会，尽可能地搜集竞争对手的信息，仔细研究招标文件，科学合理地编制投标文件，提出最具竞争力的报价。

2.2 综合评估博弈模型应用

2.2.1 竞争对手报价预测

通过 SWOT-CLPV 分析，中铁 X 局决定采用竞争型报价策略，即假设其投标报价既不是所有有效投标报价最大值也不是最小值。对于其余 5 家竞争对手 (分别用投标人 1 至 5 表示)，其历次报价与最优报价如表 4 所示。

依据表 4 中的数据，采用公式 ⑺ 可以计算出竞争对手历次报价偏差系数，如表 5 所示。

依据表 5，采用公式 ⑻ 对其余 5 家竞争对手历次报价与最优报价的偏差系数进行计算，得到竞争对手报价平均偏差系数如表 6 所示。

利用平滑系数 α 计算，依据经验 α 取值为 0.6。采用公式 ⑽ 计算，竞争对手本次投标报价偏差系数预测如表 7 所示。

由于在计算评标基准价公式中需要舍去有效投标人报价的最高值和最低值，因而此次报价中舍去投标人 3 与投标人 4 的报价，根据表 7 中的数据可以预测其余 3 家竞争对手对于最高投标限价的平均偏差为 Γ平= -0.004 5。从中铁 X 局角度进行考虑，假设此次中铁 X 局报价为最优报价记作 Z'，则可以得出竞争对手平均报价 Y1= 0.995 5 Z' 万元。

2.2.2 满分报价区间

由于 K 值为在评标会上由投标代表随机抽取，因此依据满分报价区间即公式 ⑷，确定 K 值不同的情况下各最优报价区间预测如表 8 所示。

由表 8 可以得出当调整系数 K 值不同时的各个最优投标报价，从开标情况来看，当时开标现场由投标代理人抽取的 K 值为 0.995，根据所建模型可得此时的最优报价区间，经过评审最后中铁 X 局以报价为 322 468.01 万元中标，与表 8 计算相符，因而该模型对于当前铁路工程应用的综合评估法评标方法具有适用性。

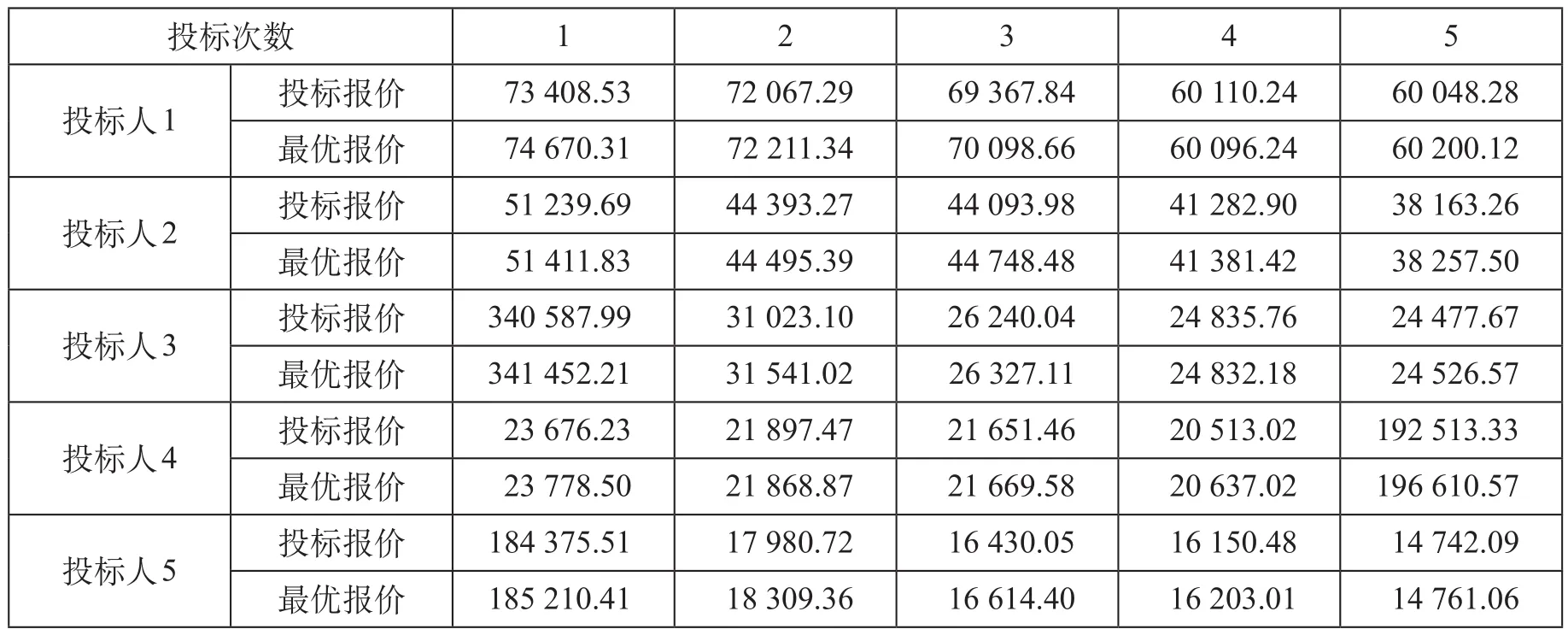
表 4 其他投标人历次报价与最优报价 万元

表 5 竞争对手历次报价偏差系数

表 6 竞争对手报价平均偏差系数

表 7 竞争对手本次投标报价偏差系数预测

表 8 最优报价区间预测 万元

3 结束语

投标竞争是铁路施工企业获得工程项目承包权的必经之路，而报价又是编制标书的核心组成部分。通过对招投标过程中施工企业与竞争对手之间的 SWOT-CLPV 及博弈分析，构建基于博弈论的铁路工程投标报价策略模型，为施工企业在招投标活动中分析竞争对手、明确其当前的投标态势，以及进行科学合理的投标报价决策提供借鉴，从而可以针对竞争对手的行动做出最有效的策略反应，提出最具竞争力的投标报价，为企业成功中标奠定基础。

[1] 梁 涛. 铁路工程总承包投标报价决策研究[J]. 铁道运输与经济，2016，38(2)：67-70. LIANG Tao. Study on Bidding Price Strategy Decition of Railway Engineering Project Contracting(EPC)[J]. Railway Transport and Economy，2016，38(2)：67-70.

[2] 李 铌，刘武成，李 亮. 基于案例推理的铁路施工项目投标报价决策研究[J]. 铁道科学与工程学报，2008，5(4)：68-73. LI Ni，LIU Wu-cheng，LI Liang. Bidding Decision-making of Railway Construction Projects based on Case-based Reasoning[J]. Journal of Railway Science and Engineering，2008，5(4)：68-73.

[3] 董小强，刘桂桢，刘瀛州，等. 基于 SWOT 分析法的铁路货运发展策略探讨[J]. 铁道货运，2016，34(2)：15-17，22. DONG Xiao-qiang，LIU Gui-zhen，LIU Ying-zhou，et al. Discussion on Strategies of Railway Freight TransportDevelopment based on SWOT Analysis[J]. Railway Freight Transport，2016，34(2)：15-17，22.

[4] 胡文发. 工程招投标与案例[M]. 北京：化学工业出版社，2008.

[5] 焦银禾. 建设工程招投标及博弈论应用[M]. 北京：中国铁道出版社，2009.

[6] 王 正. 博弈论在建筑工程中的应用[J]. 工程建设与设计，2015(6)：175-177. WANG Zheng. Application of the Game Theory in the Construction Projects[J]. Construction & Design for Engineering，2015(6)：175-177.

[7] 中国铁路总公司. 铁路建设项目施工招标投标实施细则 (试行)：[2015] 146 号[A]. 北京：中国铁路总公司，2015.

[8] 雷文华，雷鹏飞. 铁路建筑工程招投标博弈模型研究[J].甘肃科学学报，2012，24(1)：102-107. LEI Wen-hua，LEI Peng-fei. Study on the Game Model of Bidding in Railway Constructions [J]. Journal of Gansu Sciences，2012，24(1)：102-107.

责任编辑：金 颖

Tender Offering Strategies for Railway Engineering based on Game Theory

As the key factor of bidding, the tender offer plays a significant role in winning the bid and also affects the profit margin of construction enterprises. The paper analyzes the railway engineering construction enterprises and their competitors using SWOT-CLPV model from the perspective of the bidder, and suggests enterprises to plan the bidding strategy according to the current situation. Thanks to the comprehensive evaluation method, the paper establishes the tender offer model using game theory and works out the optimal tender offer range. The applicability of the model are verified by the actual railway bidding examples, thus to provide the basis for bidding price of construction enterprises.

Railway Engineering; Tender Offer; Comprehensive Evaluation Method; SWOT-CLPV Analysis; Game Theory

1003-1421(2016)12-0019-06

F532.5；O225

A

10.16668/j.cnki.issn.1003-1421.2016.12.04

2016-10-14

河北省高层次人才资助项目(2013429102)；河北省交通厅科技计划项目(2011522-26)