预制空心方桩抗弯承载力研究
王清龙,杨德健
(1. 天津城建大学,天津 300384;2. 天津建城基业集团有限公司,天津 300301)
预制空心方桩抗弯承载力研究
王清龙1,2,杨德健1
(1. 天津城建大学,天津 300384;2. 天津建城基业集团有限公司,天津 300301)
通常的混凝土受弯承载力计算均采用混凝土屈服模型.本文对预制空心方桩抗弯承载力计算采用钢筋屈服模型.在该模型基础上,推导出预制空心方桩抗弯承载力计算公式.通过对比两种计算结果表明:在构件配筋率高的情况下,按混凝土屈服模型更符合实际又偏于安全;在构件配筋率低的情况下,按钢筋屈服模型更符合实际且偏于安全.
预制空心方桩;抗弯承载力;配筋率
预制空心方桩包括先张法预应力离心混凝土空心方桩(以下简称预应力方桩)和预制钢筋混凝土空心方桩(以下简称空心方桩).近年来,预制空心方桩在工程中的应用越来越多,对其研究也日益增多.国内外学者对打桩过程中的力学机理以及多种因素下对打桩破坏的影响做了详细的研究[1-3];李志刚、刘永超等[4-5]研究了预制桩的工程应用;刘金皊等[6]研究了预制桩沉桩可行性分析实用方法;张忠苗等[7]对管桩和预制方桩的竖向承载力进行了对比分析;还有学者对其抗震进行了研究[8-9].但这些研究都是桩与地基土相结合、彼此相互作用的研究,而对桩自身的抗弯承载力的研究则没有涉及.
王广宇[10]和缪海林[11]研究了预应力方桩抗弯承载力的计算,王广宇在计算预应力方桩抗弯承载力中做了几点假定,其中包括“假定受压区预应力钢筋不参与抗弯,假定受拉区钢筋全部达到屈服”.笔者并没有做这样的假定,而是让所有的钢筋均参与抗弯承载力的计算,同时认为在中和轴附近的钢筋是没有达到屈服强度的,这一观点和缪海林的观点是一致的.从缪海林给出的预应力方桩抗弯承载力的计算公式可知,他从混凝土屈服的角度出发计算其抗弯承载力.笔者认为根据配筋的不同,混凝土和钢筋均有可能先屈服,甚至王广宇认为对预应力方桩压区混凝土的破坏几乎没有,从而说明了考虑钢筋屈服来计算预制空心方桩抗弯承载力的必要性.
1 从钢筋角度计算预制空心方桩抗弯承载力
1.1 第i排钢筋的应力值σpi的计算
预制空心方桩抗弯承载力的计算不同于一般梁截面抗弯承载力的计算.因为梁截面一般都是上下配筋,而预制空心方桩则是四面均匀配筋,具体见图1-2.
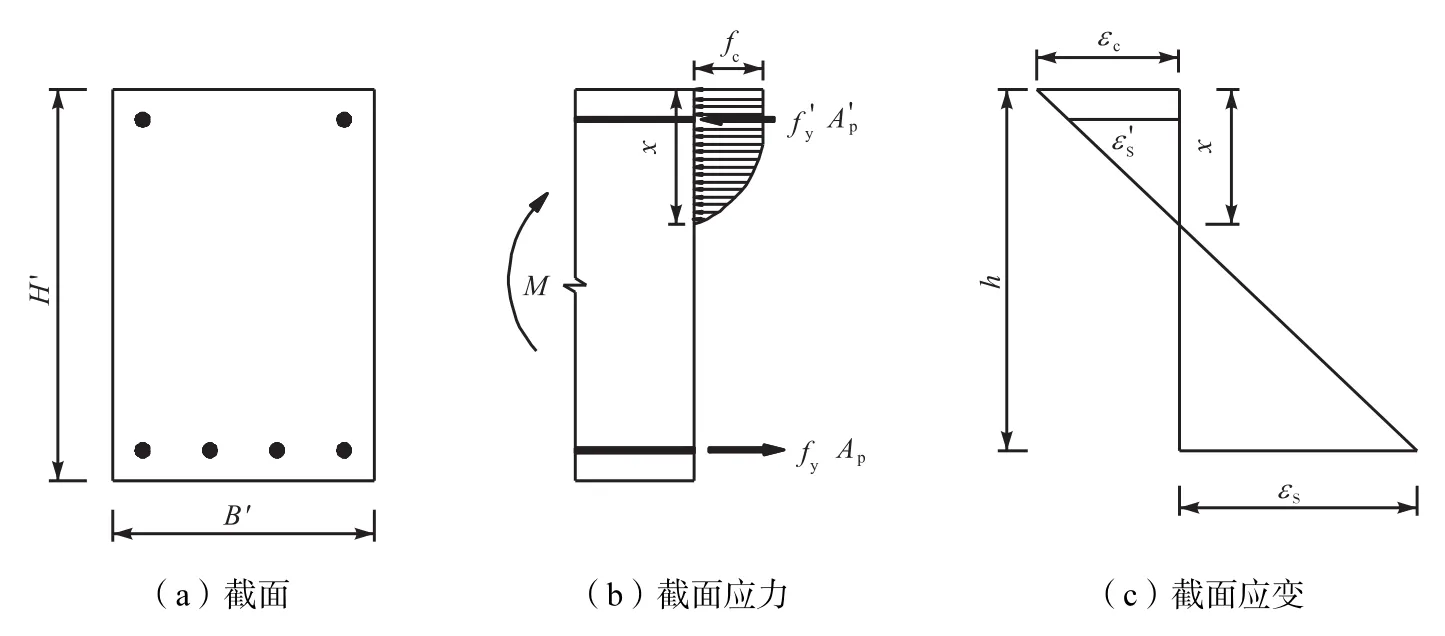
图1 梁截面计算示意
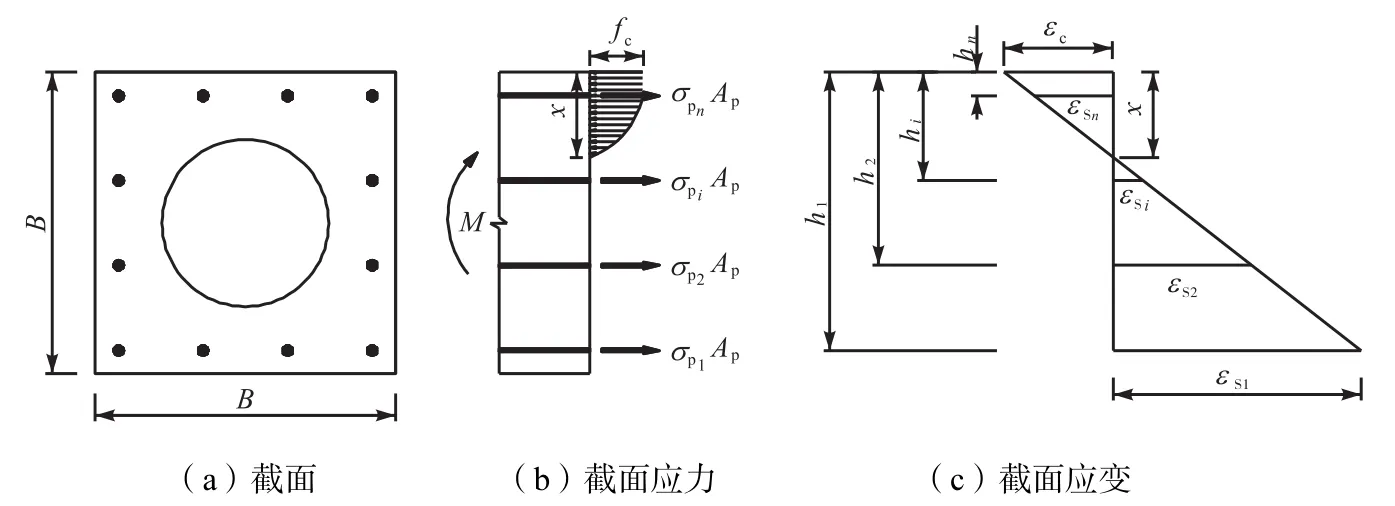
图2 空心方桩截面计算示意
第i排钢筋的应力值σpi,可根据GB50010—2010《混凝土结构设计规范》[12]中相应公式计算,但此计算公式是建立在受压区边缘纤维的应变达到混凝土的极限压应变,再根据平截面假定,利用相似三角形求出σpi.
为了从钢筋屈服角度计算预制空心方桩抗弯承载力,必须求出从钢筋屈服角度推导出的第i排钢筋的应力值σpi的计算公式,即已知εs1,求εc、 εsi(i=2,…,n).这也是本文对计算预制空心方桩抗弯承载力的贡献之一.根据文献[12]规定,纵向钢筋的极限拉应变取为0.01,即εs1=0.01.仍根据平截面假定,利用相似三角形求得普通钢筋应力
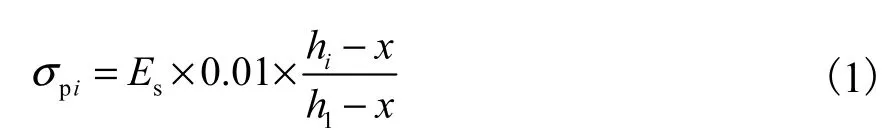
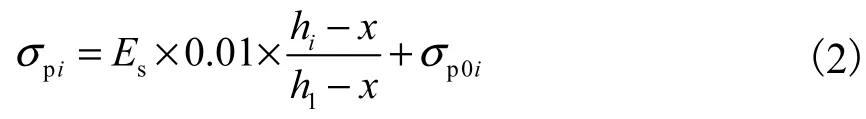
式中:Es为钢筋弹性模量;hi为第i层纵向钢筋截面重心至截面受压边缘的距离;h1为最外排钢筋截面重心至截面受压边缘的距离;x为混凝土受压区高度.
1.2 相关参数之间的关系
研究抗弯承载力,首先要确定混凝土受压应力与应变的关系.文献[12]中采用抛物线上升段和水平段的混凝土受压应力-应变关系曲线,见图3[13].
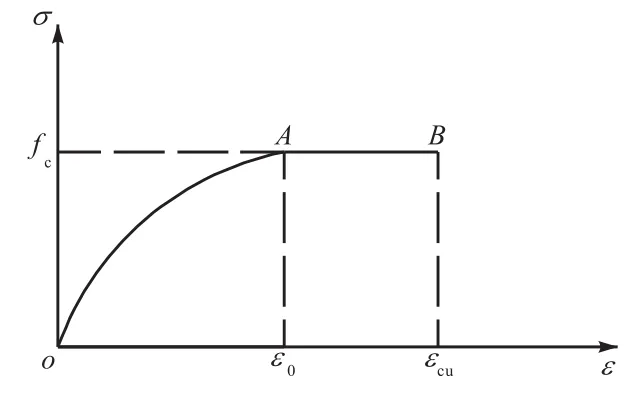
图3 混凝土应力-应变曲线
为了计算抗弯承载力,需要确定几个临界值.按文献[12]规定,纵向钢筋极限拉应变取为0.01.根据平截面假定和相似三角形,可求出相应受压区高度与混凝土压应变临界值的关系.
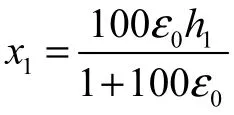
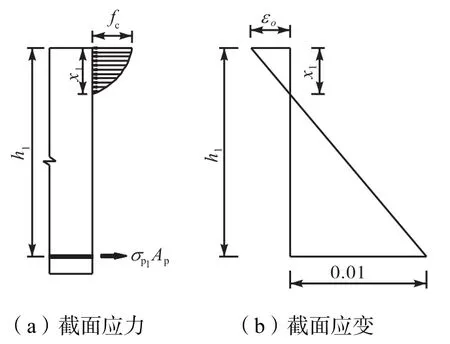
图4 x1计算示意
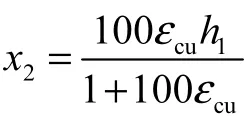
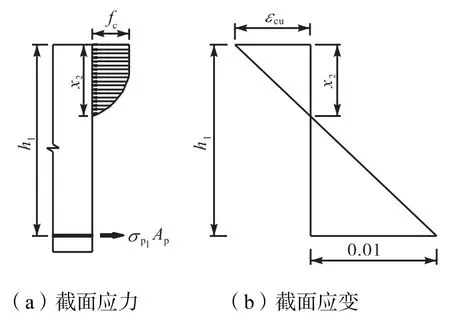
图5 x2计算示意
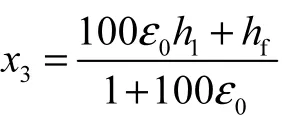
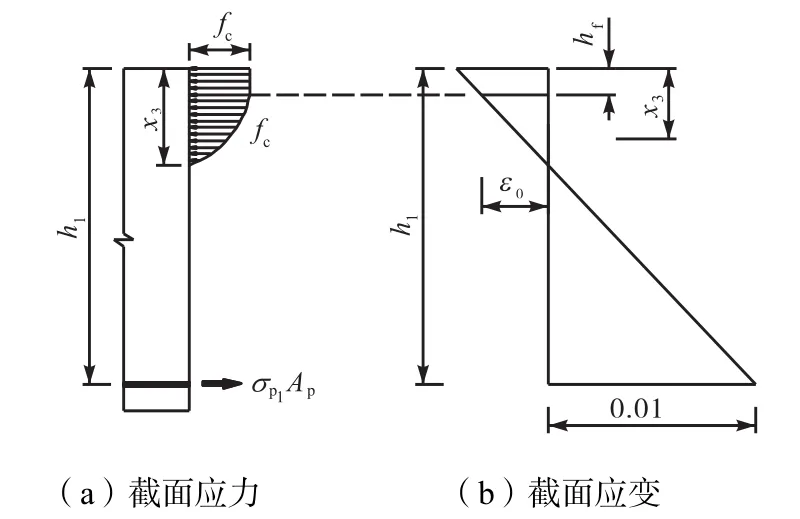
图6 x3计算示意
应变为ε0时,对应的该点距中和轴的距离,计算示意如图7所示.
1.3 抗弯承载力计算公式
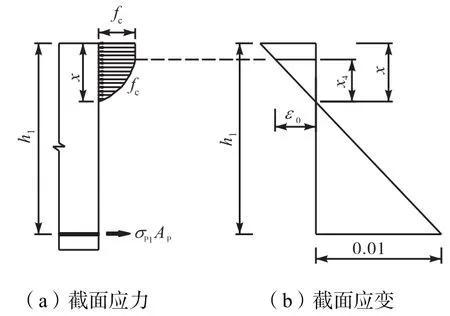
图7 x4计算示意
从钢筋屈服角度计算预制空心方桩抗弯承载力时,因为并不知道混凝土是否破坏,所以不能用等效矩形应力的方法求受压区混凝土所受压力,只能用积分的方法求混凝土所受压力以及受压区混凝土合力作用位置距中和轴的距离yc.
(1)混凝土受压区高度x小于等于受压区翼缘高度hf′(即x≤hf′).
当0<x≤x1时,即受压区混凝土应力位于图3所示OA段,由受弯构件正截面力的平衡得:
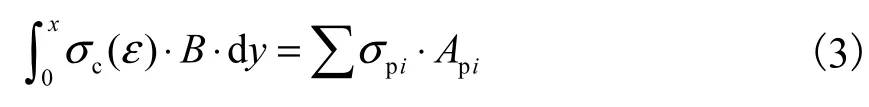
式中:B为预制空心方桩的边长,y为受压区混凝土任意一点距中和轴的距离.由式(3)求得混凝土受压区高度x,受压区混凝土合力作用位置距中和轴的距离为
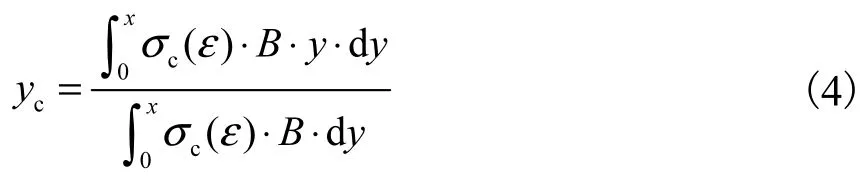
抗弯承载力
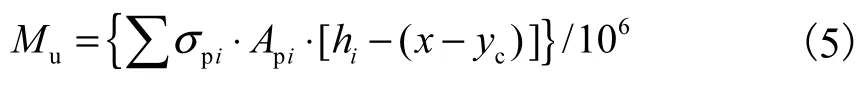
当x1<x≤x2时,即受压区混凝土应力位于图3所示OAB段,由受弯构件正截面力的平衡得:
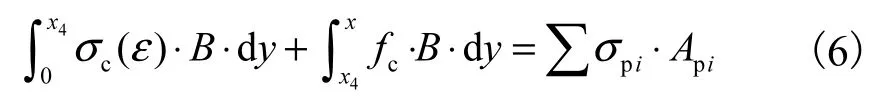
由式(6)求得混凝土受压区高度x,受压区混凝土合力作用位置距中和轴的距离为
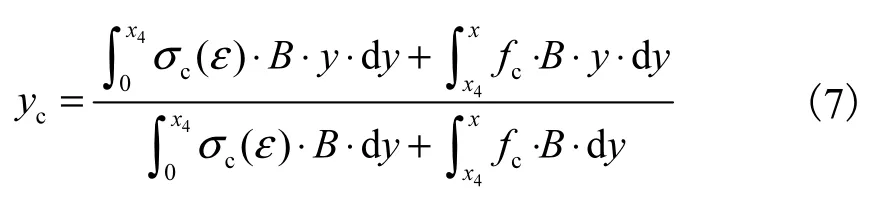
抗弯承载力按公式(5)计算.
(2)混凝土受压区高度x大于受压区翼缘高度hf′(即x>hf′).
当0<x≤x1时,即受压区混凝土应力位于图3所示OA段,由受弯构件正截面力的平衡得:
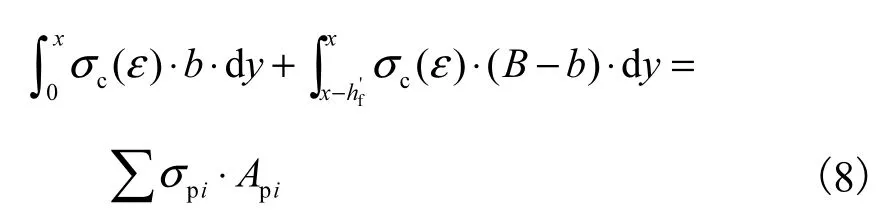
式中:B为预制空心方桩的边长;b为空心方桩截面换算成等截面、等惯性矩的I型截面的腹板宽度;y为受压区混凝土任意一点距中和轴的距离.由式(8)求得混凝土受压区高度x,受压区混凝土合力作用位置距中和轴的距离为
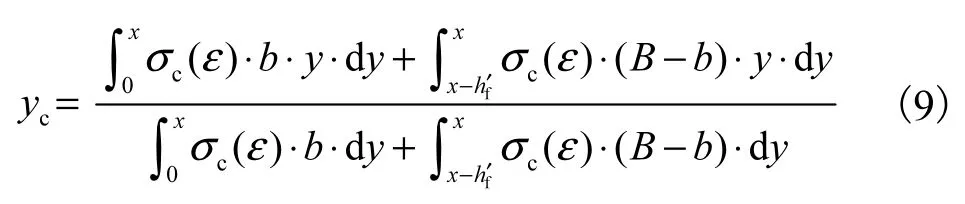
抗弯承载力按公式(5)计算.
驰腾科技有限公司董事长詹友林对《中国经济周刊》表示:“中国是全世界独一无二的全方位智能手机市场,但还有很多国家通信比较落后,中低端、功能机的市场还很大。现在电子行业开始向西部转移,我们来泸州,一是因为泸州在政策上大力支持,比如厂房三年免租,登记办证一对一服务,后期保障到位。二是因为劳动力市场大,员工在这里生活更经济、也更安心。”
当x1<x≤x2,且x≤x3时,即受压区混凝土应力位于图3所示OAB段,此时受压区翼缘处混凝土应力部分位于OA段,部分位于AB段,由受弯构件正截面力的平衡得:
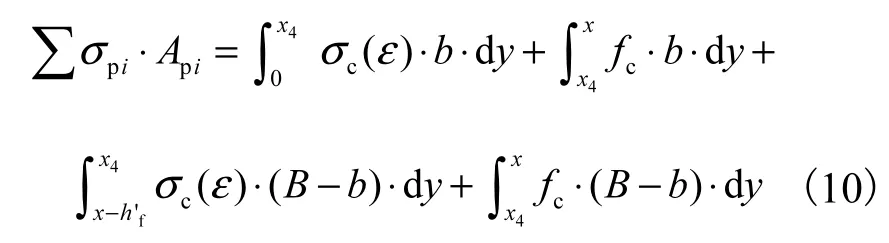
由式(10)求得混凝土受压区高度x,受压区混凝土合力作用位置距中和轴的距离为
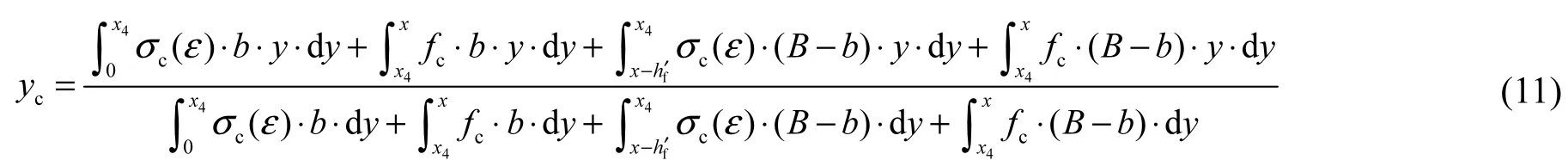
抗弯承载力按公式(5)计算.
当x1<x≤x2,且x>x3时,即受压区混凝土应力位于图3所示OAB段,此时受压区翼缘处混凝土应力均位于AB段,由受弯构件正截面力的平衡得:
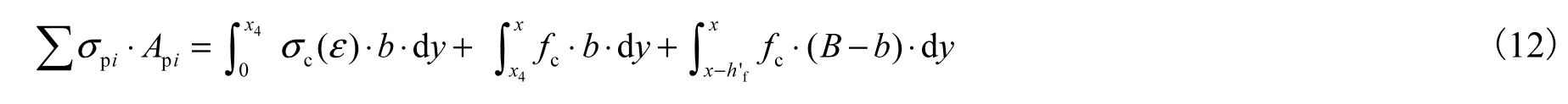
由式(12)求得混凝土受压区高度x,受压区混凝土合力作用位置距中和轴的距离为
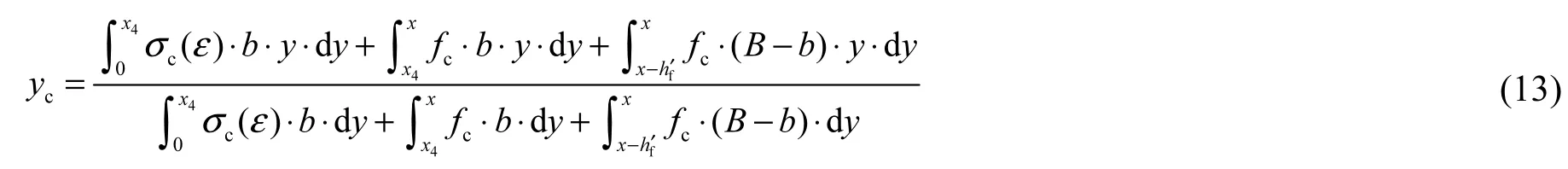
抗弯承载力按公式(5)计算.
应当说明,当求得的混凝土受压区高度x>x2时,表明该构件配筋太多,为超筋破坏,本公式不适用.
2 两种方法计算结果的对比分析
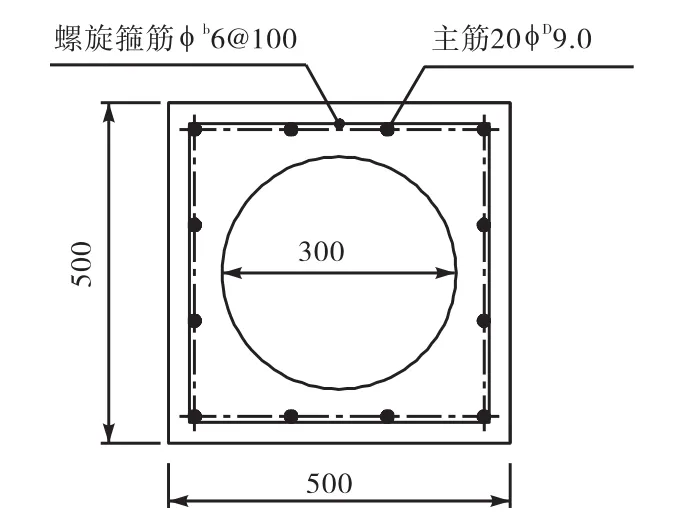
图8 Z1配筋
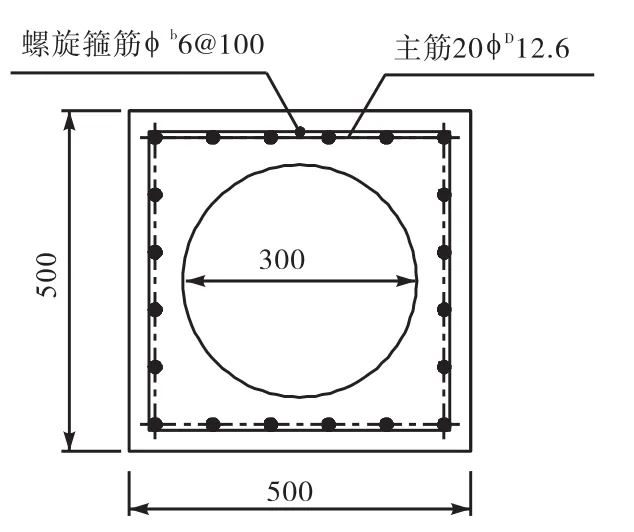
图9 Z2配筋
对空心方桩Z1、Z2分别从混凝土屈服和钢筋屈服两种不同破坏模型计算其抗弯承载力,计算结果详见表1-2.

表1 Z1抗弯承载力统计表

表2 Z2抗弯承载力统计表
从表1可以看出:Z1采用混凝土屈服模型计算的抗弯承载力比采用钢筋屈服模型计算的抗弯承载力大.这是因为Z1的配筋率仅为0.43%,,配筋率很低,因此空心方桩在受弯过程中,混凝土并没有完全发挥作用,而钢筋却完全发挥了作用.故采用混凝土屈服模型,即混凝土能够充分发挥作用的模型,由于过多考虑混凝土的作用,从而导致其计算结果会偏大一些.
从表2可以看出:Z2采用钢筋屈服模型计算的抗弯承载力比采用混凝土屈服模型计算的抗弯承载力大.这是因为Z2的配筋率为1.83%,,配筋率很高,因此空心方桩在受弯过程中,钢筋并没有完全发挥作用,而混凝土却完全发挥了作用,故采用钢筋屈服模型,即钢筋能够充分发挥作用的模型,由于过多考虑钢筋的作用,从而导致其计算结果偏大.
综上所述,桩的配筋率的大小决定了哪种计算模型比较准确,但这个配筋率并没有一个定值,因此在计算预制空心方桩抗弯承载力时,宜采用两种模型分别计算,取其较小值,这样即偏于安全,又符合实际的破坏形态.
3 结 论
(1)本文建议性地给出了从钢筋屈服的角度,计算第i排钢筋的应力值σpi的公式以及计算预制空心方桩抗弯承载力的公式;
(2)在计算预制空心方桩抗弯承载力时,宜采用混凝土屈服模型和钢筋屈服模型分别计算,取其较小值,这样的计算结果既偏于安全,又符合实际的破坏形态;
(3)按钢筋屈服模型计算预制空心方桩抗弯承载力,是对计算预制空心方桩抗弯承载力方法的一种丰富和发展,它使得预制空心方桩抗弯承载力的计算更全面,从而更好地为预制空心方桩在工程中的应用发展提供更可靠的技术支持.
[1] 刘屠梅. 基桩检测技术与实例[M]. 北京:中国建筑工业出版社,2006.
[2] RAUSCHE F,GOBLE G G,LIKINS G. Dynamic determination of pile capacity[J]. J Geotech Eng,1985,111(3):367-383.
[3] 张亚南,冯 春,李世海,等. 混凝土预制桩在冲击荷载作用下的破坏机理研究[J]. 建筑结构,2013(增刊1):876-881.
[4] 李志刚,张雁朱,合 华,等. 预应力高强空心桩(管桩和方桩)工程应用分析[J]. 建筑结构,2014(8):1-5.
[5] 刘永超,朱明亮,王清龙,等. 预应力矩形支护桩在滨海软土深基坑工程中的应用研究[J]. 土木工程学报,2015(增刊1):168-173.
[6] 刘金皊,张益凡,李 娜,等. 预制桩沉桩可行性分析实用方法[J]. 建筑结构,2013(11):92-97.
[7] 张忠苗,喻 君,张广兴,等. PHC管桩和预制方桩受力性状试验对比分析[J]. 岩土力学,2008(11):3,059-3,065.
[8] 刘陕南,高承勇,侯胜男,等. 上海地区建筑桩基水平抗震设计初步探讨[J]. 建筑结构,2013(7):88-93.
[9] 倪国泉,杨 军,潘 鹏,等. 预应力混凝土空心方桩承台节点抗震性能试验研究[J]. 地震工程学报,2013(2):246-251.
[10] 王广宇. 预应力混凝土空心方桩成套技术研究[D]. 北京:中国科学建筑研究院,2007:86-88.
[11] 缪海林. 江苏省空心方桩图集新旧版本内容差异分析[J]. 江苏建筑,2013(1):93-106.
[12] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范:GB50010—2010[S]. 北京:中国建筑工业出版社,2010:34-40.
[13] 王铁成. 混凝土结构原理[M]. 天津:天津大学出版社,2002:56-61.
Research of Flexural Capacity of Precast Hollow Square Piles
WANG Qinglong1,2,YANG Dejian1
(1. Tianjin Chengjian University,Tianjin 300384,China;2. Tianjin City Construction Group Co.,Ltd,Tianjin 300301,China)
Usually the concrete yield model is used to calculate concrete flexural bearing capacity. In this paper,the steel yield model is used to calculate the bearing capacity of precast hollow square pile. On the model basis,the calculation formula of bearing capacity of precast hollow square pile is derived. According to the comparision,a conclusion indicates that the concrete yield model is real and safe when reinforcement ratio of precast hollow square pile is big;meanwhile,the steel yield model is real and safe when reinforcement ratio of precast hollow square pile is small.
precast hollow square piles;flexural bearing capacity;reinforcement ratio
TU473.1
A
2095-719X(2016)06-0427-05
2015-11-06;
2016-03-08
王清龙(1983—),男,河北沧州人,天津建城基业集团有限公司工程师,天津城建大学硕士生.

