基于IDA的大跨网架结构竖向地震动力性能研究

张辉东，戚国营，闫 立

(天津城建大学 a. 天津市土木建筑结构防护与加固重点实验室；b. 土木工程学院，天津 300384)

土木工程

基于IDA的大跨网架结构竖向地震动力性能研究

张辉东a,b，戚国营a,b，闫 立a,b

(天津城建大学 a. 天津市土木建筑结构防护与加固重点实验室；b. 土木工程学院，天津 300384)

大跨空间网架结构具有跨度大、竖向刚度低、阻尼小、对竖向地震作用比较敏感等特点，因此，在竖向地震作用下，对该类结构体系非线性动力性能的研究尤为重要．基于有限元法，针对我国某地区一实际大跨网架结构，对其进行竖向地震激励下的动力性能研究，采用增量动力分析(IDA)方法对该结构进行了抗震性能评价，得到了该结构的薄弱位置及倒塌极限．研究表明：该网架结构具有良好的竖向抗震性能；随着结构塑性发展，IDA曲线的离散性明显；结构概率分位50%,对应的倒塌极限位移为0.337,m；薄弱构件主要分布于下弦，尤其是下弦节点附加质量区域，且杆件的塑性发展集中于附加质量区域．

大跨网架结构；抗震性能；增量动力分析；倒塌

大跨空间结构以其优点发展迅速，广泛用于车站、机场、会堂、体育馆等大面积屋盖公共建筑中，其中应用最广泛的当属网架结构．大跨网架结构跨度大、阻尼小、平面外刚度低，对竖向地震响应较敏感，其产生的局部或整体倒塌对人民生命财产造成的损失极大．因此，对竖向地震激励下该类结构薄弱部位及倒塌问题的研究显得尤为重要．

针对网架结构的竖向抗震分析，张毅刚等[1]利用子空间迭代法研究了网架结构的自震特性，利用反应谱法和时程分析法研究了竖向地震作用下的内力分布规律；丁万尊等[2]在考虑阻尼的情况下，利用拟夹层板法分析了竖向地震激励下网架结构的动力问题；沈祖炎等[3]认为网架结构的竖向振型为主要振型，竖向激励对加速度响应具有放大作用；三向地震作用下，竖向地震处于主导地位；孙梦涵等[4]认为不可忽视竖向地震对网架变形的影响，是否考虑下部支承刚度对结构的竖向地震响应影响较小；黄兴淮等[5]提出网架结构在竖向强震作用下的倒塌破坏机理，认为弦杆首先发生屈曲，进行内力重分布，某一关键杆件的失效会产生多米诺骨牌效应，最终导致结构整体倒塌；韩庆华等[6]对大跨格构式拱结构进行增量动力分析(IDA)，分析结果与实验数据一致，验证了IDA方法在空间结构体系性能评价方面的准确性；孟凡林等[7]利用IDA方法对大跨网架结构进行了单条地震动响应研究，获得结构的倒塌极限及薄弱区域，为网架结构的多条地震动IDA提供了一种参考．

增量动力分析(incremental dynamic analysis，简称IDA)方法，是一种建立在非线性动力时程分析基础之上的动力参数分析理论．这种方法最早由Bertero[8]提出，之后由Vamvatiskos和Cornell[9]进行了系统性研究和改进，并被FEMA350[10]和FEMA351[11]标准采用，现已广泛用于基于性能的结构抗震评价．IDA理论的基本原则是调整地震动记录的强度幅值IM，以此作为输入激励进行非线性动力时程分析，获得不同IM值下的结构响应值DM．IDA涵盖了结构在地震激励下的整个变化过程，对结构从弹性到屈服、从屈服到塑性发展，直至结构倒塌作出全面评估，反映结构在不同强度地震作用下的承载力、刚度及位移变化，以此评价结构的整体抗震性能．

近年来，IDA理论作为一种强有力的非线性分析方法[12]被国内广泛接受，成为解决工程问题的有力手段，其分析数据可以精确地反映出结构随地震动强度的改变而发生的变化[13]，能较好地评价结构的抗震性能．目前，基于IDA方法的研究主要集中于框架、框剪等结构形式，对于网架等空间结构在竖向地震作用下的性能分析较少．本文以某实际网架结构为例进行增量动力分析，研究该结构在竖向地震激励下的刚度变化、最大节点位移、薄弱部位以及倒塌问题，评估该结构的抗震性能．

1 模型方程

1.1 结构的运动方程

根据动力学相关理论[14]，该网架结构的动力方程表示为

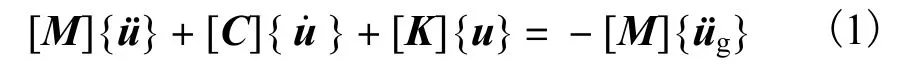
式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为结构刚度矩阵；{üg}为地震激励加速度；{u}为节点位移向量；{˙}为节点速度向量；{ü}为节点加速度向量．

其中，结构刚度[K]为常量，当结构进入塑性后，其整体刚度与运动的时间历程{u(t)}及材料的非线性相关，随着塑性的发展程度不断变化．考虑地震动的随机性和弹塑性响应中结构刚度的变化，将式(1)表示为

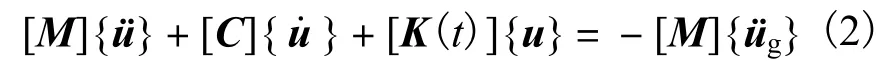
式(2)中，[K(t)]表示t时刻结构的刚度矩阵，其他参数意义如式(1)．

1.2 阻尼模型

阻尼属于结构的基本动力属性，用来描述结构振动过程中的综合耗能能力，是影响结构动力问题的关键因子之一．因此，阻尼模型的合理选取对于结构的动力分析十分关键．非线性增量动力分析中，常采用瑞利(Rayleigh)阻尼，考虑到高阶振型对阻尼的影响，曾提出多种修正的Rayleigh阻尼模型，如张辉东等[15]提出了一种适用于网架结构的节点-构件阻尼模型．考虑到本文的研究重点和分析精度要求，选择瑞利阻尼模型[14]

式中：α、β分别表示质量比例阻尼和刚度比例阻尼，均为未知系数．根据振型正交性，α、β与振型阻尼比之间的关系为

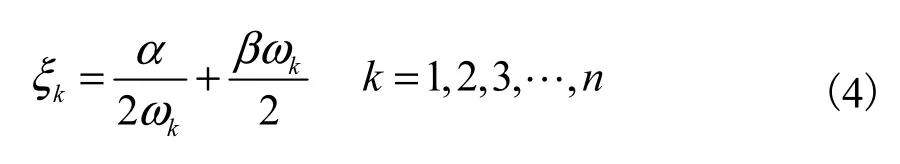
由式(4)可以看出：任意给定两个阻尼比，就可确定α、β系数．阻尼比取值直接影响着弹塑性分析中的地震响应，GB50011—2010《建筑抗震设计规范》[16]规定：该类型网架的阻尼比取值0.02．曹资等[17]认为空间结构的阻尼比随着振型的增加而增大，随结构的塑性发展而增大，最大值可达0.05；此外，弹塑性分析中考虑材料非线性相当于考虑了塑性阻尼，同时考虑材料非线性和塑性阻尼会放大结构的阻尼作用[18]．因此，在满足分析要求的前提下，一般指定结构的阻尼比相等，本文阻尼比取值为0.03．

另外，Rayleigh阻尼与结构的振型相关，选择参考振型应考虑对结构动力响应有重要影响的频率分量，一般情况下，取前2阶自振频率确定阻尼系数[19-20]．

2 IDA方法

IDA方法分为单记录IDA法和多记录IDA法：前者属于确定性分析，而地震动的随机性和不确定性决定了该法并不能准确评估结构在未知地震作用下的破坏特性和趋势；后者应选择足够多的地震动记录，且记录包含结构可能遭受的最强地震动部分，符合此类条件的多条IDA曲线才能全面、准确地评估结构的抗震性能．

IDA方法是指对已选用的某条地震动记录根据需要进行调幅，得到单调增大的一组地震动记录，以此作为输入激励，对结构进行非线性动力时程分析，得到结构响应参数，直到结构倒塌失稳为止．根据一系列IM值和DM值，绘制对应于此条地震动的IDA曲线．重复以上步骤，即得到多条IDA曲线．关键步骤如下．

(1)地震动记录选取．时程分析中，地震动记录的选择对结构的性能分析十分关键．根据场地类别和地震分组等条件，选择频谱特性相接近的地震动记录．

为满足IDA方法对地震强度变化的要求，需调整地震动记录．初始地震波强度峰值的调整公式为

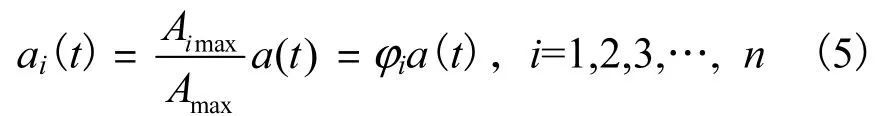
式中：ai(t)、Aimax为第i次调整后的地震波曲线及强度峰值；a(t)、Amax为初始地震波曲线及强度峰值；φi为调幅系数．Vamvatiskos和Cornell[9]提出一种“Hunt&fill”原则确定φi；吕大刚等[21]曾提出一种“折半取中”的原则确定φi．本文采用等步调幅．

地震动持时是影响时程分析的重要因素．持时不同，输入能量不同，结构损伤不同，结构响应有所区别．地震动持时应包含地震动最强记录时段；文献[16]规定：地震波的持续时间不宜小于结构自振周期的5倍和15,s．本文输入地震波持时20,s．

(2)IM、DM参数的选择．对于空间结构体系，最常采用峰值加速度(PGA)作为强度参数IM[6]．结构的抗震性能水平和抗破坏能力可由结构某参数或自定义指标来确定，例如层间位移角、最大节点位移等．

(3)极限状态点的确定准则．强震作用下，杆件塑性发展，结构刚度退化，结构响应发散，即结构失效倒塌；此外，可从最大位移角度评价结构极限状态；FEMA规定[11]：结构的倒塌破坏准则，即单条IDA曲线调幅前后两点的连线斜率小于0.2倍的弹性斜率时，则取调幅前的点作为极限点．本文极限状态点的确定参考此类准则．

3 网架实例

3.1 网架模型

采用河北某实际网架作分析算例：结构7度(0.10g)设防，Ⅱ类场地，地震分组第2组；正放四角锥双层网架，纵向长度136,m，横向长度120,m，网架高度2.5,m，网格大小4,m×4,m；高强螺栓节点连接；采用下弦多点支撑，下部支撑采用箱型和H型截面钢柱，柱距分别为8，24，28,m，柱网布置见图1．钢材采用Q345钢，杆件截面及荷载分布见表1，其中附加质量以吨(t)计．3.2 荷载

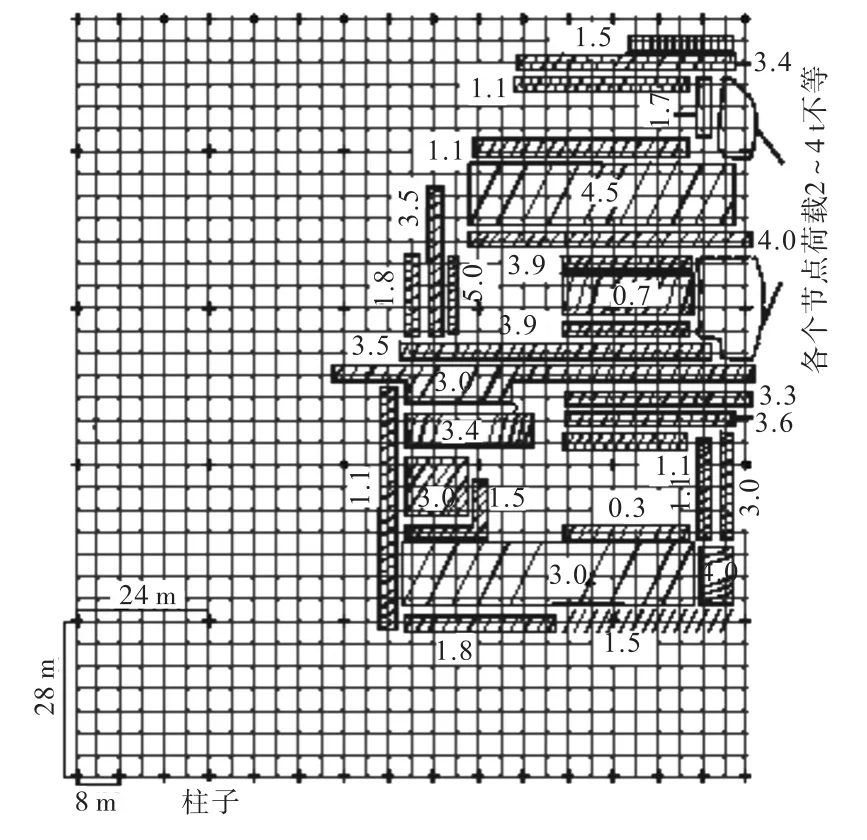
图1 柱网布置及节点附加质量分布

表1 杆件规格及荷载分布

对于网架结构，荷载均作用于节点，杆件不承受横向荷载，将上弦均布荷载等效为节点处的集中力，表示为

式中：qi表示均布荷载；A表示节点所承担荷载的面积．对表1均布荷载，据式(6)等效为恒载FG＝AqG＝16×0.40＝6.4,kN，活载FQ＝AqQ＝16× 0.50＝8.0,kN．

根据杆件截面参数和材料参数，程序自动计算杆件的自重，网架节点的重量一般取杆件自重的30%,．

3.3 数值模型

研究该网架结构的竖向地震响应，可将下部支撑简化为三向铰支[4]，对本文研究内容的影响在可控范围内．有限元分析模型中，钢材采用双线性随动硬化模型；采用杆单元模拟，每个杆件离散为一个分析单元，杆件两端弯矩释放．有限元模型见图2.考虑非线性重力荷载的初始条件，采用非线性直接积分的方法进行弹塑性分析，积分方法采用Newmark-β法．该结构阻尼采用瑞利阻尼，阻尼比取为0.03．分析过程需同时考虑结构的几何非线性和以塑性铰为表征的材料非线性．杆件中部设置延性轴力铰，铰长度取值

图2 有限元模型

式中：LP为铰长度，塑性变形长度范围；L0为杆件计算长度．塑性铰代表杆件出现塑性变形(杆件易损)，易损准则为

式中：A表示毛截面面积；σcr表示屈服极限应力值，与长细比λ有关；Pcr表示极限轴力．

4 结果与分析

综合考虑地震动震级、场地土和结构周期等因素，从PEER强地震动数据库[22]中选取9条地震动记录作为输入样本，见表2．文献[16]规定，7度设防的时程分析加速度取值：小震35,cm/s2，中震105,cm/s2，大震220,cm/s2．通过调幅分别取PGA为0.035g、0.105g、0.22g、0.3g、0.4g、0.5g、0.6g、0.7g、0.8g等直至结构倒塌．

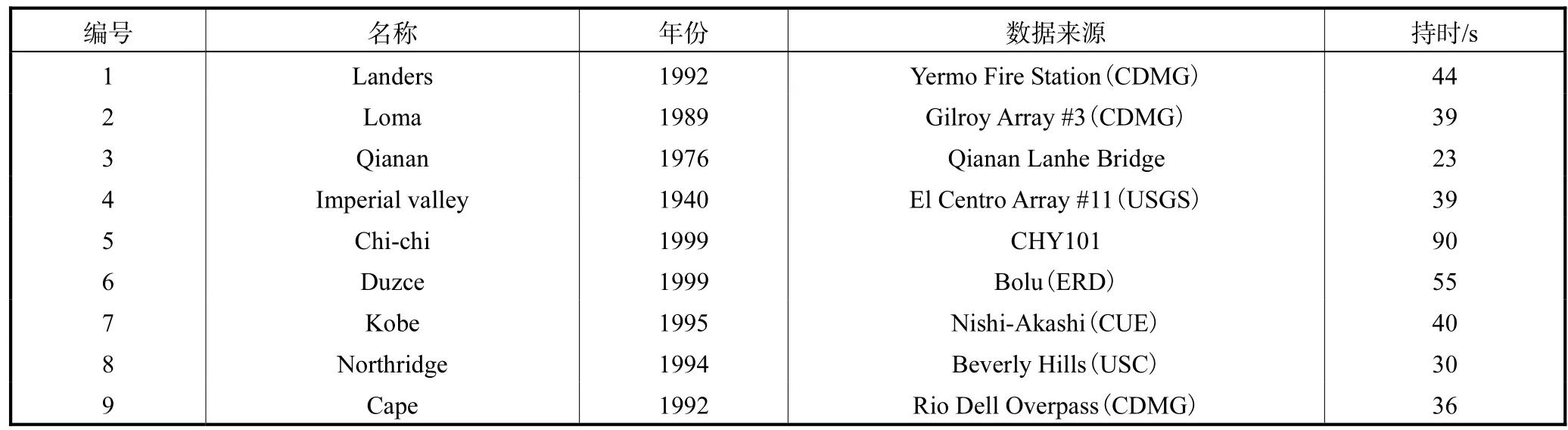
表2 地震动参数

4.1 结构的整体响应分析

采用PGA作为输入参数IM，竖向最大节点位移作为DM，通过数值分析绘制结构在不同输入样本下的IDA曲线，如图3所示．

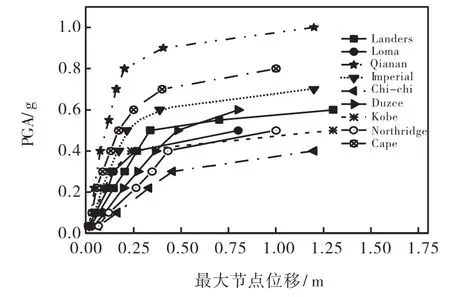
图3 竖向最大节点位移

由图3可知：不同地震动对应的IDA曲线差异性较大，尤其随着地震动强度的增加，离散性愈明显，这主要由地震动的随机性所决定．但从IDA曲线簇来看，该结构在不同地震作用下的响应趋势是一致的，大体经历弹性、弹塑性、塑性三个阶段．各个IDA曲线初始部分斜率较大，均存在一个线弹性阶段[23]，因为小震作用下，杆件没有塑性发展，结构处于弹性阶段．随着地震动强度的增大，部分杆件由弹性状态进入弹塑性状态，结构刚度降低，表现为曲线斜率不同程度的减小．随着输入强度的继续增大，塑性发展加剧，结构的破坏继续发展，IDA曲线斜率急剧降低，即在很小IM增幅的情况下，损伤指标DM产生不成比例的增加，明显存在斜率突变点(刚度退化点)，即预示着结构倒塌破坏．

竖向地震作用下，结构在PGA为0～0.22g范围内未出现刚度退化极限，说明7度大震作用下，该网架结构没有倒塌破坏，其设计是安全的．

在上述分析数据基础上，利用统计方法得到竖向地震作用下，结构概率分位值10%,、50%,、90%,对应的倒塌极限位移分别为0.234，0.337，0.440,m，见图4．50%,分位代表该结构在可能遭遇地震下的平均响应水平，即结构最大位移达到0.337,m时即可视为倒塌破坏，10%,和90%,分位代表结构极限位移的离散程度．4.2 基于单条IDA的响应分析

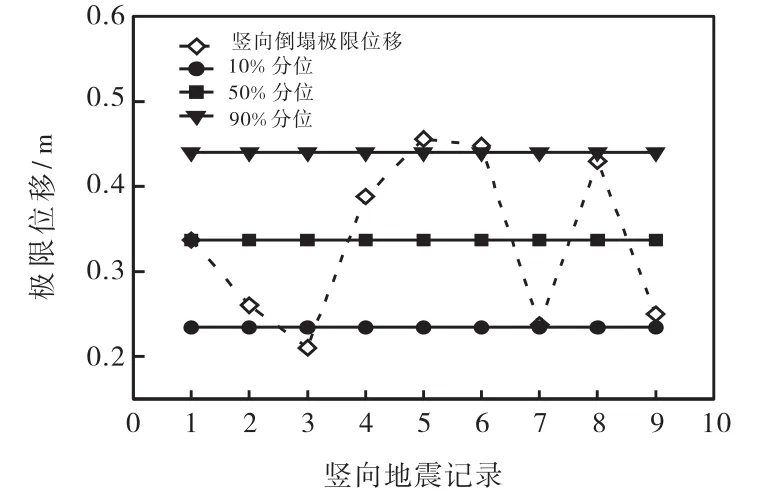
图4 倒塌极限位移值

以Kobe波为例(见图5)，介绍该网架的竖向地震响应：最大节点位移、杆件轴力、易损杆件分布及结构薄弱区域等．

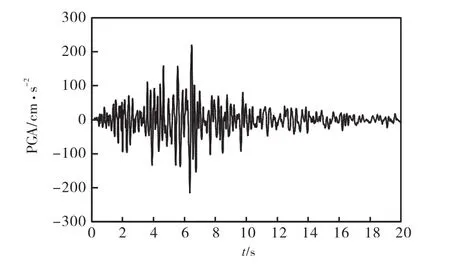
图5 Kobe地震动记录

4.2.1 基于Kobe波的响应分析

大震PGA＝220,cm/s2作用下，位移最大的节点(505)的加速度和位移时程曲线见图6-7．取代表性杆件#3127、#3159、#3158为研究对象，得到其轴力时程曲线见图8-10，节点及杆件定位见图11标示．

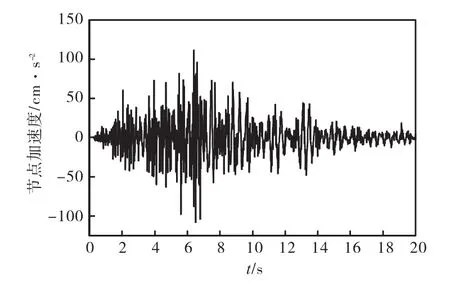
图6 505节点加速度时程曲线

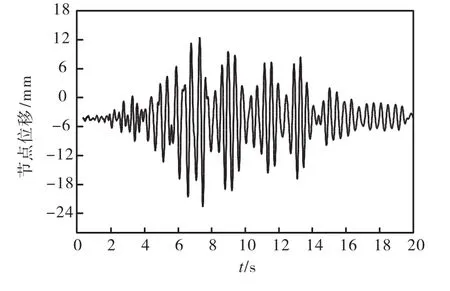
图7 505节点z向位移时程曲线

由图5-7可以看出：最大节点位移时程曲线与加速度时程曲线基本一致，说明在大震作用下，该结构整体始终处于弹性阶段；位移峰值的响应稍滞后于加速度峰值，这是结构振动过程中由阻尼作用产生的合理响应．

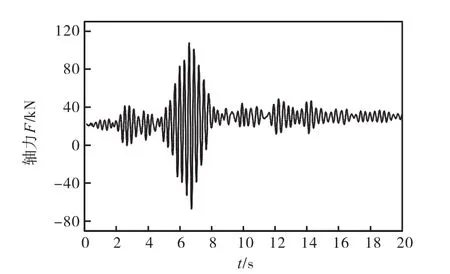
图8 #3127轴力时程曲线

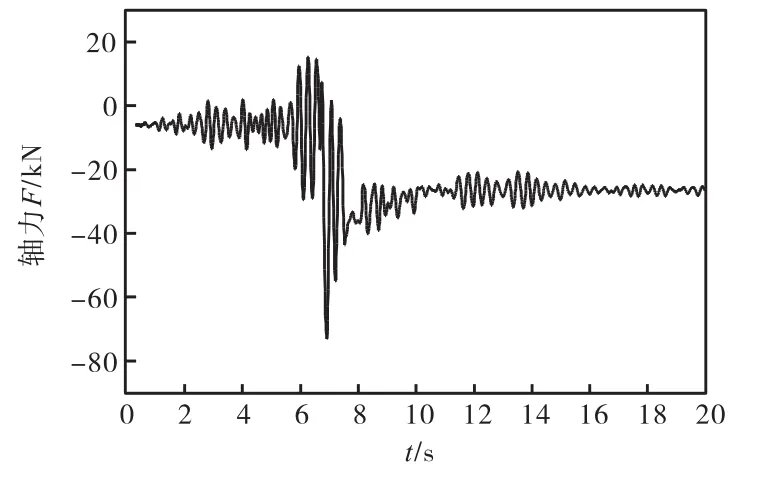
图9 #3159轴力时程曲线

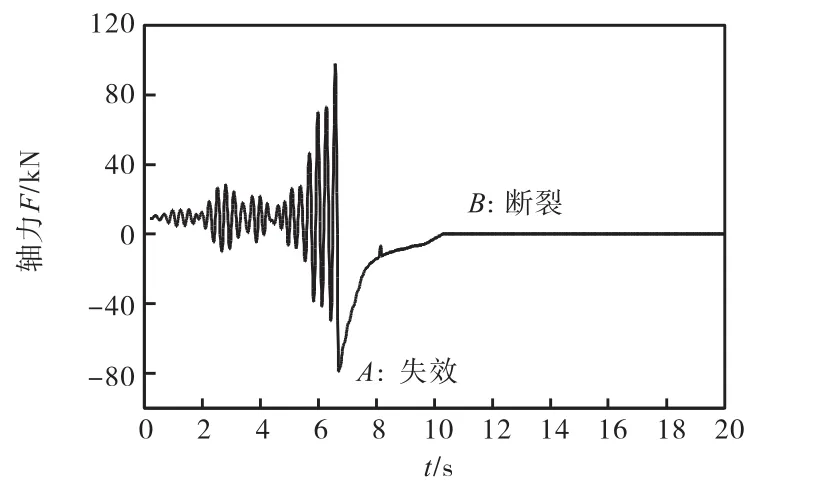
图10 #3158轴力时程曲线

分析图8-10知：在大震激励过程中，#3127虽有铰出现，但杆件塑性变形极小，可近似认为处于弹性阶段，其轴力时程曲线与地震波曲线(见图5)基本一致；#3159在地震激励6.5,s左右轴力突变，杆件发生塑性变形，承载能力急剧减小，之后随地震动强度的变化重新回到弹性工作状态；#3158在地震作用6.7,s左右于A点出现轴力极值，杆件在A点发生塑性破坏，轴力不再随地震激励的改变而改变，经历3.5,s之后于点B处变为0，说明该杆件断裂，退出工作．

4.2.2 薄弱构件分布

程序中材料的非线性由塑性铰体现，铰出现的先后次序及分布表明了结构中的易损杆件及薄弱区域分布．地震激励PGA＝220,cm/s2作用下，结构下弦于2.47,s首现失效杆件(铰)，自2.47～5.00,s时段，地震强度较小，结构杆件均处于弹性状态(无铰出现)；从5～8,s时段内，包含地震动最强部分(见图5)，且前期输入能量不断累积，下弦多个杆件发生塑性变形．当输入样本PGA＝500,cm/s2,时，结构于12.48,s倒塌破坏．图11-12为PGA＝220，500,cm/s2(第12,s)作用下结构薄弱杆件的分布．由图11-12可大致看出该结构的易损杆件、薄弱区域的分布，为该类型结构的设计和加固提供一种参考．竖向地震作用下，该网架薄弱杆件大部分位于上、下弦杆，腹杆极少存在塑性变形；与上弦杆相比，下弦失效杆件数量较多，且多集中于附加质量节点区域；节点附加质量越大，产生地震力越大，杆件发生塑性变形的可能性相应增加．此外，薄弱杆件的分布比较集中，结构中某一单元的失效会导致连锁反应，初始破坏单元的失效，引起与之相互作用的单元发生连锁失效[5]，最终导致结构的整体失稳．因此，网架结构设计时，要特别注意附加质量节点区域杆件的设计．

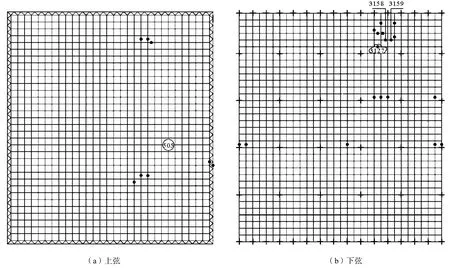
图11 PGA为220,cm/s2,上、下弦薄弱杆件分布

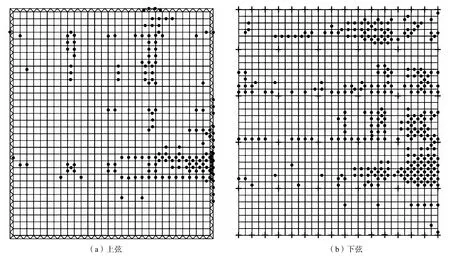
图12 PGA为500,cm/s2,(第12,s)上、下弦薄弱杆件分布

5 结 论

(1)基于IDA方法的动力性能研究可以较好地评估网架结构的抗震性能，为竖向地震作用下网架结构的整体倒塌破坏研究提供一种方法．

(2)该网架结构具有良好的抗震性能，在设防烈度7度的不同地震动大震激励下，虽有不同程度、不同数量塑性铰的出现，但均没有整体倒塌，该结构设计是合理、经济和安全的．

(3)随着塑性发展，结构的非线性得以体现，IDA曲线的离散性明显．结构概率分位50%,对应的倒塌极限位移为0.337,m，即最大位移达到0.337,m时即可视为结构倒塌破坏．

(4)竖向地震作用下，网架结构的弦杆为薄弱杆件，且下弦杆塑性铰数目较上弦杆多；杆件的塑性发展集中于附加质量区域．在此类型网架设计时，要注意附加质量区域杆件的设计，以防该区域杆件的塑性发展导致局部失稳及整体倒塌的危险．

［1］ 张毅刚，蓝惆恩. 网架结构在竖向地震作用下分析方法[J]. 建筑结构学报，1985，6(5)：2-14.

［2］ 丁万尊，陈庆云. 正交正放类网架结构动力响应的拟夹层板分析法[J]. 建筑结构学报，1997，18(1)：18-25.

［3］ 沈祖炎，陈学潮，陈扬冀. 网架结构模型抗震实验研究[J]. 土木工程学报，1994，27(1)：30-40.

［4］ 孙梦涵，范 峰，支旭东，等. 考虑下部支承四角锥网架结构动力响应分析[J]. 土木工程学报，2014：47(12)：10-16.

［5］ 黄兴淮，徐赵东，杨明飞. 多维地震下大跨网格结构倒塌分析与抗倒塌分析[J]. 东南大学学报，2012，42(1)：109-113.

［6］ 韩庆华，卢 燕，徐 颖，等. 基于IDA的格构式结构倒塌能力研究性能分析[J]. 土木工程学报，2015，48(3)：1-7.

［7］ 孟凡林，孟祥瑞，徐德英，等. Sap2000在大跨空间结构抗震分析设计中的应用[J]. 吉林建筑工程学院学报，2011，28(4)：1-4.

［8］ BERTERO V V. Strength and deformation capacities of buildings under extreme environments[J]. Structural Engineering and Structure Mechanics，1977，53(1)：29-79.

［9］ VAMVATISKOS D，CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structure Dynamics，2002，31(3)：491-514.

［10］ FEMA. Recommended seismic design criteria for new steel moment-frame buildings：FEMA-350[R]. Washington，D.C.：Federal Emergency Management Agency. SAC Joint Venture，2000.

［11］ FEMA. Recommended seismic evaluation and upgrade criteria for existing welded steel moment-frame buildings：FEMA-351[R]. Washington，D.C.：Federal Emergency Management Agency．SAC Joint Venture，2000.

［12］ VAMVATISKOS D，CORNELL C A. Applied incremental dynamic analysis[J]. Earthquake Spectra，2004，20(2)：503-522.

［13］ VAMVATISKOS D，CORNELL C A. Direct estimation of seismic demand and capacity of multi-degree of freedom systems through incremental dynamic of single degree of freedom approximation incremental[J]. Journal of Structural Engineering，2005，131(4)：589-599.

［14］ CHOPRA A K，谢礼立，吕大刚，等. 结构动力学：理论及其在地震工程中的应用[M]. 北京：高等教育出版社，2005：276-277，339-341.

［15］ 张辉东，王元丰. 空间网壳结构的节点-构件阻尼模型研究[J]. 土木工程学报，2015，48(2)：55-61.

［16］ 中华人民共和国住房和城乡建设部．建筑抗震设计规范：GB50011—2010[S]. 北京：中国建筑工业出版社，2010：32-315．

［17］ 曹 资，薛素铎，王雪生，等. 空间结构抗震分析中的地震波选取和阻尼比取值[J]. 空间结构，2008，14(3)：4-8.

［18］ 杨志勇，黄吉峰，田家勇. 罕遇地震弹塑性静、动力分析方法中结构阻尼问题的探讨[J]. 地震工程与工程振动，2009，29(6)：116-120.

［19］ 何 利，叶献国. 不同阻尼模型对框架结构地震反应影响因素[J]. 合肥工业大学学报(自然科学版)，2011，34(7)：1 028-1 030.

［20］ 李 田. 结构时程动力分析中的阻尼取值研究[J]. 土木工程学报，1997，30(3)：68-73.

［21］ 吕大刚，于晓辉，王光远. 基于单地震动记录IDA方法的结构倒塌分析[J]. 地震工程与工程振动，2009，29(6)：34-39.

［22］ Pacific Earthquake Engineering Research Center. PEER ground motion database[DB/OL]. [2014-10-25]. http：// ngawest2. berkeley. edu/.

［23］ 李 磊，郑山锁，李 谦. 基于IDA的型钢混凝土框架的地震易损性分析[J]. 广西大学学报，2011，36(4)：536-541.

Analysis on the Vertical Seismic Performance of a Large Span Grid Structure Based on IDA Method

ZHANG Huidonga,b，QI Guoyinga,b，YAN Lia,b
(a. Tianjin Key Laboratory of Civil Buildings Protection and Reinforcement；b. School of Civil Engineering，TCU，Tianjin 300384，China)

The large span space grid structure is highly sensitive to the vertical component of the seismic action due to the large span，low vertical stiffness and its small damping property，therefore，a research of nonlinear dynamic behaviors on this structural system subjected to the vertical seismic component is particularly important．Based on the finite element method，the nonlinear dynamic behaviors of a real large span grid structure located in a region of China are investigated under earthquake actions．The seismic performance of the structure is evaluated using the Incremental Dynamic Analysis(IDA)method．The weak location and collapse ultimate point of the structure is obtained．Results show that the structure has a good seismic performance；the difference among the IDA curves is remarkable as plasticity development of members．It is observed that the collapse limit displacement of 50%,probability is 0.337 m，and that weak members occur at the lower region where the masses are assigned.

large span grid structure；seismic behavior；incremental dynamic analysis；collapse

TU393.3

A

2095-719X(2016)06-0416-07

2015-10-25；

2016-03-02

国家自然科学基金青年基金(51108301)

张辉东（1976—），男，山东青岛人，天津城建大学教授，博士.