多齿侧间隙传动系统非线性特性研究

方禹鑫， 丁 千， 张 微

4(天津大学 机械工程学院，天津 300072)

多齿侧间隙传动系统非线性特性研究

方禹鑫， 丁 千， 张 微

4(天津大学 机械工程学院，天津 300072)

舵机系统是典型的机械传动系统，传动过程中的部件间隙对系统动力学特性有很大影响。针对多级齿轮和丝杠螺母组合的舵机系统，建立含有齿侧间隙和内部激励误差的平动-扭转运动动力学方程，采用谐波平衡法分析系统的固有频率及周期运动幅频响应，利用数值方法求解、分析传递误差、碰撞和分岔与混沌运动现象，并分析讨论了多间隙和单间隙对系统动力学特性的影响差别。该分析成果可以为舵机系统结构和操作参数的优化设计、提高传动效率和平稳性提供参考。

舵机系统；间隙；非线性；动态传递误差

机械传动系统应用广泛，其工作性能可以影响至整个设备，对周围环境也有很大影响。在航空航天领域中，舵机是最主要的机械传动系统，是一种多齿轮啮合、多间隙的系统，且性能要求更高。近几十年来，齿轮动力学的研究一直受到广泛关注。李润方等[1]对齿轮传动系统的建模方法、模型的类型以及非线性因素等方面作了深入和系统的研究。王建军等[2]评述了国内外时变轮齿啮合刚度参数振动问题和齿侧间隙非线性振动问题的研究进展。对于单对齿轮的动态特性，KAHRAMAN等[3-5]给出了基于实验的非线性动力学模型，考虑内部激励和外部激励，从数值和解析两方面给出动态响应分析。多齿轮对啮合方面，LIN等[6-8]通过数值和解析的方法给出了行星齿轮的振动特性和固有频率特性。SHEN等[9]利用增量谐波平衡法对含有时变刚度和静态传递误差的单齿轮啮合进行了解析求解，给出了增加阻尼和降低激励幅值对于增强系统稳定性的作用。ZHANG等[10]对于含有时变刚度和立方非线性的单齿轮对系统进行了数值和解析求解，得出了系统的超谐响应和非线性振动特性。唐进元等[11]研究了间隙对含摩擦和时变啮合刚度的动力系统动力学的影响。高建平等[12]对4自由度直齿轮非线性方程组采用基于打靶法的局部参数延拓法进行了数值求解。胡鹏等[13]采用数值方法研究了伺服刀架动力传动系统在不同转速，不同的啮合刚度的作用下，输入端和输出端齿轮对的动态传递误差和动态啮合力的变化趋势。王晓笋等[14]计算了齿轮系统周期状态和混沌状态下的相空间轨线，庞加莱截面和关联维数，并进一步分析其动力学特性的变化情况 。

本文针对一类含有多级齿轮和丝杠滑块结构的舵机系统，建立了考虑间隙和静态传递误差因素的非线性动力学模型，并利用基于离散傅里叶变换的谐波平衡方法和数值方法研究系统的动力学特性，分析不同转速和间隙情况的动力学规律，为提高舵机系统动力学特性的优化设计提供参考。

1 间隙非线性动力学模型

图1(a)是一类含多级齿轮和丝杠滑块结构的舵机传动系统示意图。假设传动轴和轴承具有足够大的刚度，齿轮对啮合力作用在啮合线方向并忽略各处界面的摩擦效应，可以将系统简化为图1(b)所示的集中质量模型力学模型。其中Ii,Ri和θi(i=1,2,3)分别为齿轮的转动惯量、分度圆半径和转角，m4，R4和φ分别为滑块的质量、丝半径和升角，Km,Kn，Kl和Cm,Cn，Cl分别为系统的综合啮合刚度和阻尼，e(t)为齿轮对的静态传递误差，T1和F4为加载于第一级齿轮和滑块上的系统载荷。

图1 舵机传动系统

为研究系统运行中齿轮的拍击和相对位置变化，引入各运动体之间的相对位移

x1=R1θ1-R2θ2-em(t)

(1)

x2=R2θ2-R3θ3-en(t)

(2)

x3=-x4+R4θ3tanφ-el(t)

(3)

建立系统动力学方程如下

(4)

(5)

(6)

(7)

其中em、en、el为一级、二级齿轮间和滑块丝杠间的静态传递误差表达式为[15-16]

e(t)=-ersin(ωrt+φ)，r=m,n,l

(8)

式中:er为静态传递误差的幅值;ωr为齿轮的啮合频率;φ为相位角。外部振动激励T1的激励频率与齿轮啮合频率的关系为(Z-齿轮1的齿数)

ωr=Z*ωt，r=m,n,l

(9)

函数f(x)是齿侧间隙的非线性函数，可表示为

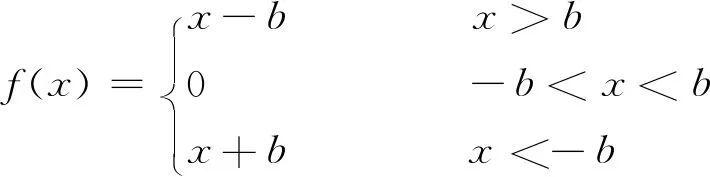
(10)

式中:b为啮合齿轮对的半侧隙。

引入如下无量纲变量

式中:ω0，b0分别为频率和间隙的基准值。将相对位移式(1)～式(3)带入动力学方程式，整理后得到无量纲形式系统相对运动方程为

(11)

(12)

(13)

令Bi=bi/b0，则无量纲间隙可以表示为

(14)

2 稳态运动的幅频响应

2.1 基于离散傅里叶变换的谐波平衡法求解

本节采用基于离散傅里叶变换的谐波平衡法，求解系统的稳态运动响应。

当载荷矢量和齿轮啮合刚度变化周期为T(频率为Ω)时，可以将其展开为Fourier级数

(15)

(16)

(17)

由于x(τ)是周期为ηT的函数，f(τ)同样是周期为ηT的函数，可以展开为

(18)

至此，动力学方程的所有项均已经展开成级数形式。把式(15)～式(18)代入动力学方程式(11)～式(13)，令方程组两边的常数项、各阶正弦谐波和余弦谐波的系数相等，得到(2R+1)N个方程构成的代数方程组(19)，求解方程组Si=0，即可求解得到x(θ)的各项系数。

(19a)

(19b)

(19c)

r=1,2,…R

在上述方程组中，系数ur为待求未知量。由于f(x)为x的函数，其Fourier展开式的各项系数fr也是未知量ur的函数。为了求解方程组式(19)，采用Fourier变换和逆变换得到fr和ur的函数关系。首先，通过离散Fourier变换的逆变换得到x(t)在一个周期的时域内的离散序列xn

(20)

n∈[0,N-1]

进而求得x(t)的时间序列xn对应的fr的时间序列gn

gn=f(xn)

(21)

其次，对函数f(x)的离散时间序列gn进行Fourier变换，得到频域内的Fourier系数fr

(22)

至此，得到了一组关于ur的非线性代数方程组。首先假设一组初始解ur，采用拟牛顿法进行迭代，求解得到式(19)的稳态解。

2.2 稳态幅频响应

根据对一个实际传动结构进行测量和有限元计算的结果，取齿轮分度圆半径R1=10 mm，R2=18 mm，R3=33 mm，计算得到转动惯量I1=2.6×10-7kg×m2，I2=3.0×10-7kg×m2，I3=3.7×10-6kg×m2。滑块质量m4=0.055 kg，刚度系数Km=1.148×108N/m，Kn=1.147×108N/m，Kl=6.287×109N/m。根据经验公式，齿轮啮合阻尼的取值范围为C=[0.015, 0.085][17-18]，误差激励的幅值的量纲级别取值为间隙大小的1/10。由于载荷会随着系统负载和运行状态而改变，这里假设初始载荷F11为0.2，其载荷参数根据平衡原理推导得出。

假定齿轮对的间隙相同，计算给出了系统稳态运动情况下的幅频变化(见图2)。由图2可知，间隙b=0时，三个固有频率分别是0.66，1.10和1.85。随着间隙的增加，系统刚度弱化，固有频率随之减小，共振振幅增加且出现非线性跳跃现象。其中与第一阶频率相比，第二阶和第三阶的振幅相对较小，对于间隙更加敏感，因此间隙变化带来的刚度软化现象更为显著，故共振幅值变化也更为明显。

图2 舵机系统幅频响应

3 含间隙非线性系统的动力学特性

3.1 多间隙影响下的复杂响应

为分析含多个间隙的齿轮系统的复杂响应，我们采用RUNGE-KUTTA法计算求解方程组式(11)～式(13)(令b=1.2×10-4，与图2(c)对应)。计算表明，随着转速变化，各级轮对的振动特点基本相同，因此本文只给出了第一级齿轮对相对位移的分岔图、动态啮合误差(DTE)均值、齿轮啮合比例和DTE均方根幅值，见图3。分岔图显示的复杂运动现象反映了多个间隙的影响。当转速Ω处于0～0.4的范围内，系统振动是单周期的，仅存在齿轮的正面啮合，振动均方根幅值相对较小而且连续。当转速Ω增大到0.4～0.6区间，即进入第一阶固有频率范围，振动均方根幅值明显增加，振动平均位置则有所下降，但开始出现齿轮拍击现象。当转速Ω继续增大到0.6～1.8区间后，运动显示出混沌特征，振动均值、均方根幅值均明显震荡，齿轮啮合状态呈现双侧拍击。此后，系统运动交替进入相对稳定和混沌状态，脱齿、正面拍击和均值、均方根幅值跳跃现象增多，说明转动愈快，啮合间隙非线性的影响愈大，会引起很大的转动噪声。

图3 第一级齿轮对动态啮合特性(间隙b=1.2×10-4 m)

从图3可知，由于存在间隙非线性，2阶、3阶共振的周期运动已经被复杂运动替代或掩盖，且伴随着系统的振动平衡位置不稳定、齿轮拍击等现象，影响系统的稳定性和传动效率。

图4～图5分别给出了较高转速(Ω=2.32和Ω=3)时的时间历程、相图、庞加莱映射和频谱图。相对稳定的运动是倍周期运动(Ω=2.32)，而混沌状态(Ω=3)，的时间历程和相图表现为无序状态，频谱图包含更为丰富的频率成分。

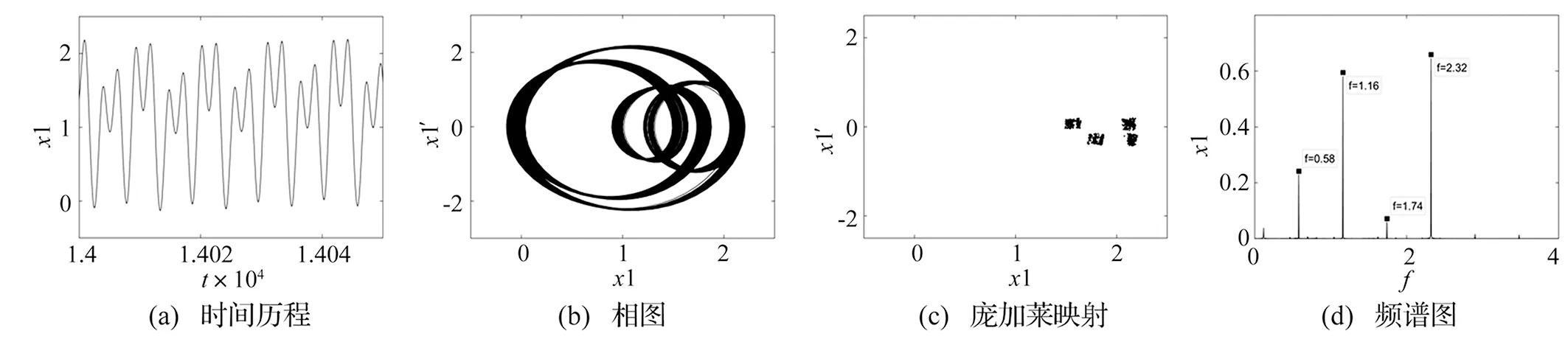
图4 Ω=2.32时系统的响应

图5 Ω=3系统的响应

3.2 单间隙时的系统动力学特征

仅有一个齿轮对存在间隙时，轮对相对位移的振动特征(分岔图)如图6所示。其中图6(a)、图6(b)、图6(c)是仅存在一级齿轮间隙时的情况。可以看到，当间隙较小时(图6(a))，系统的线性幅频特性相对明显，能够清晰的看到各阶共振峰值，且振幅较大的一阶、二阶共振基本是单频振动。随着间隙增大，系统的非线性特性逐渐表现出来。一方面，线性固有频率处的振动变成复杂的多频甚至混沌振动；另一方面，最大振幅出现的频率位置发生变化，逐渐向二阶固有频率靠近。

分析还发现，在一阶固有频率的2倍频附近(区间[1.2，1.6])出现了混沌响应，在3倍频之后(区间[1.9,2.0])出现多频振动现象。间隙的增加对二阶模态固有振动特性的影响是最明显的，即造成固有频率降低、振幅增加，并且振动的复杂程度也最明显。

图6(d)、图6(e)是分别在二级、三级齿轮存在间隙的振动情况(大小均为1.5×10-4)。二级齿轮存在间隙时，在二阶固有频率的2倍频之后(区间[1.6,2.4])和3倍频之后(区间[3.0,3.7])的响应都是混沌的。三级传动间隙的特征为一阶固有频率的2倍频之后(区间[1.4,1.6])和区间[2.3,2.5]内出现混沌响应，以及[1.6,2]的区间内的多周期响应和分岔现象。还可看出，由于x3处丝杠和滑块的啮合刚度值最高，对于间隙非线性更为敏感，对于同样大小的间隙量，三级间隙对系统动力学影响程度最大。

比较图3(a)和图6，多间隙系统的响应包含了单间隙系统的特征，并且呈现了各间隙影响叠加的状态，突出表现为在一阶共振之后，复杂的多频甚至混沌运动持续更大范围，几乎不再有单频振动。因此，可以通过合理间隙调整，控制整个工作频段的系统振动特性。

图6 不同间隙情况下的系统分岔图

4 结 论

本文针对一类含间隙和传递误差的舵机系统，建立了动力学模型，分析其固有频率、周期幅频响应、动态传递误差、运动分岔等，得到如下结果:

(1)齿轮传动系统中的间隙不仅弱化了系统刚度，造成固有频率降低，还会使其周期振动出现幅频跳跃，分岔和混沌等非线性现象，并造成传动过程中的齿轮拍击、传动不稳定和噪声，对高精度控制和机构整体稳定造成影响。

(2)对于间隙造成的不稳定现象，间隙数量和大小对传动机构影响的差别表现在：多间隙系统的响应表现为单独间隙在各自特定区域内的非线性特性的叠加，且随着间隙的增加呈现复杂响应增强，导致线性特性被非线性响应覆盖的现象。

[ 1 ] 李润方，王建军．齿轮系统动力学振动、冲击与噪声[M]．北京：科学出版社，1997．

[ 2 ] WANG J, LI R, PENG X. Survey of nonlinear vibration of gear transmission systems[J]. Applied Mechanics Reviews, 2003, 56(3): 309-329.

[ 3 ] KAHRAMAN A, SINGH R. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration, 1990, 142(1): 49-75.

[ 4 ] KAHRAMAN A, SINGH R. Non-linear dynamics of a geared rotor-bearing system with multiple clearances[J]. Journal of Sound and Vibration, 1991, 144(3): 469-506.

[ 5 ] KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system[J]. Journal of Sound and Vibration, 1991, 146(1): 135-156.

[ 6 ] LIN J, PARKER R G. Analytical characterization of the unique properties of planetary gear free vibration[J]. Journal of Vibration and Acoustics, 1999, 121(3): 316-321.

[ 7 ] LIN J, PARKER R G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Sound and Vibration, 1999, 228(1):109-128.

[ 8 ] LIN J, PARKER R G. Mesh stiffness variation instabilities in two-stage gear systems[J]. Journal of Vibration and Acoustics, 2002, 124(1): 68-76.

[ 9 ] SHEN Y, YANG S, LIU X. Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method[J]. International Journal of Mechanical Sciences, 2006, 48(11): 1256-1263.

[10] ZHANG W, DING Q. Torsion vibration and parametric instability analysis of a spur gear system with time-varying and square nonlinearities[J]. International Journal of Applied Mechanics, 2014, 6(1): 1450007.

[11] 陈思雨，唐进元．间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响[J]．机械工程学报，2009，45(8)：119-124． CHEN Siyu, TANG Jinyuan. Effect of backlash on dynamics of spur gear pair system with friction and time-varying stiffness[J]. Journal of Mechanical Engineering, 2009，45(8)：119-124．

[12] 高建平，方宗德，杨宏斌．具有时变啮合刚度传动误差及间隙的齿轮系统动力学分析[J]．航空学报，1999，20(5)：440-444． GAO Jianping, FANG Zongde, YANG Hongbin. Dynamic analysis of spur gear pairs with time-varying mesh stiffness and clearance non-linearity[J]. Acta Aeronautica Et Astronautica Sinica，1999，20(5)：440-444．

[13] 胡鹏，路金昌，张义民．含时变刚度及侧隙的多级齿轮系统非线性动力学特性分析[J]. 振动与冲击, 2014,33(15):150-156. HU Peng, LU Jinchang, ZHANG Yimin. Non-linear dynamic feature analysis of a multi-stage gear system with time-varying mesh stiffness and backlash[J]. Journal of Vibration and Shock, 2014,33(15):150-156.

[14] 王晓笋，巫世晶，周旭辉,等．含侧隙非线性齿轮传动系统的分岔与混沌分析[J]. 振动与冲击，2008, 27(1): 53-56. WANG Xiaosun, WU Shijing, ZHOU Xuhui. Bifurcation and chaos in a nonlinear dynamic model of spur gear with backlash[J]. Journal of Vibration and Shock, 2008, 27(1): 53-56.

[15] ÖZGÜVEN H N, HOUSER D R. Dynamic analysis of high speed gears by using loaded static transmission error[J]. Journal of Sound and Vibration, 1988, 125(1): 71-83.

[16] CHEN G, CHEN G, LI Y, et al. Dynamic analysis of a face-gear drive with spur involute pinion with backlash considered[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(9):1244-1234.

[17] KASUBA R, EVANS J W. An extended model for determining dynamic loads in spur gearing[J]. Journal of Mechanical Design, 1981, 103(2):398-409.

[18] WANG K L, CHENG H S. A numerical solution to the dynamic load, film thickness, and surface temperatures in spur gears, part I: analysis[J]. Journal of Mechanical Design, 1981, 103(1):177-187.

Non-linear dynamic features of a steering gear system with backlashes

FANG Yuxin, DING Qian, ZHANG Wei

(School of Mechanical Engineering, Tianjin University, Tianjin 300072, China)

A steering Gear system plays an important role in various transmission systems. Here, the dynamic behavior of a steering gear system with several backlashes was studied. Firstly, the equations of motion of a 3-DOF dimensionless system were established. Then the harmonic balance method was used to analyze the natural frequencies and amplitude-frequency responses of the system. Secondly，the system was also numerically solved with Runge-Kutta method and bifurcation, chaos and other complex dynamic phenomena were analyzed. Finally, influences of gear backlashes on dynamic features of the system were analyzed. The results indicated that both the operating parameters and the structural parameters of the steering gear system can be designed optimally to avoid undesirable dynamic motions and realize better mechanical properties.

steering gear system; backlash; non-linear dynamics; dynamic transmission error

国家自然科学基金(11272228;51575378;11332008)；天津市自然科学基金(13JCZDJC34900)

2015-10-30 修改稿收到日期：2015-12-07

方禹鑫 男，硕士，1990年生

丁千 男，教授，博士生导师，1963年4月生

TU318;P315.9