基于奇异摄动法的FFFSR全局滑模跟踪控制及ESO振动抑制

庞哲楠， 张国良， 羊 帆,2， 吴 戈， 陈志侃

(1. 第二炮兵工程大学，西安 710025； 2. 宝鸡市高新技术研究所，宝鸡 721000)

基于奇异摄动法的FFFSR全局滑模跟踪控制及ESO振动抑制

庞哲楠1， 张国良1， 羊 帆1,2， 吴 戈1， 陈志侃1

(1. 第二炮兵工程大学，西安 710025； 2. 宝鸡市高新技术研究所，宝鸡 721000)

针对存在参数不确定性和有界干扰的情况，讨论了自由漂浮柔性空间机器人(FFFSR)关节轨迹跟踪控制与柔性振动主动抑制的问题。利用奇异摄动法将系统分解为关节轨迹跟踪的慢变子系统和描述柔性振动的快变子系统，进而提出含慢、快变控制项的组合控制器;设计一种改进的全局滑模函数，利用低通滤波器抑制滑模抖振，实现全局鲁棒、快速收敛的关节轨迹跟踪;对于快变子系统，采用扩张状态观测器(ESO)对不易测量的柔性模态坐标导数和不确定扰动进行估计，并结合LQR方法，对柔性振动进行主动抑制。数值仿真表明，该组合控制器可以在有效抑制柔性振动的同时实现对期望关节轨迹的稳定跟踪。

自由漂浮柔性空间机器人；奇异摄动法；全局滑模控制；低通滤波器；扩张状态观测器；不确定性

由于空间在轨作业要求机器人具有质量轻、手臂长和负载大等特点，将空间机器人的杆件设计为轻质细长杆件，既可减小发射质量，又可节约发射成本。为获得较好的控制精度和性能，需考虑空间机器人杆件的柔性[1-3]。在实际工程应用中，柔性空间机器人必须具备在不确定条件下仍能实现关节轨迹跟踪和柔性振动抑制的能力。文献[4]针对柔性空间机器人及参数不确定动力学模型，将神经网络与传统反馈PI控制相结合，提出一种混合性机器人逆模学习控制方法。文献[5]针对参数不确定和外部扰动的情况，提出一种任务空间内自适应控制与反步法结合的控制器设计方法，实现对期望轨迹的跟踪控制。文献[6]提出一种针对自由漂浮柔性空间机器人(Free-Floating Flexible Space Robot,FFFSR)模型不确定性的神经网络自适应控制方法。由于包含振动模态的柔性机器人系统动力学方程阶数较高，且柔性杆件的振动频率一般比其关节或惯性空间的刚性运动频率要高得多。而上述方法将刚性运动控制方案和柔性振动抑制方案在同一时间尺度上进行叠加，势必会影响到刚性运动控制系统的鲁棒性和稳定性。文献[7]建立了一类高阶柔性机械臂的奇异摄动模型并进行了仿真实验。文献[8]则运用奇异摄动法建立了基体振动机械臂系统的动力学方程。上述研究主要将奇异摄动法应用于柔性地面机器人，对于基座与臂杆存在动力学耦合关系的柔性空间机器人研究较少。同时，从节省控制燃料、增加空间机器人在轨寿命的角度考虑，对载体位置和姿态均不受控的研究非常必要[9-10]。本文采用奇异摄动法将FFFSR系统降阶分解为两种时间尺度的奇异摄动模型，避免了在同一时间尺度下关节轨迹跟踪和柔性振动抑制方案简单叠加的问题。

全局滑模控制(Global Sliding Mode Control,GSMC)具有对参数摄动和外界干扰的不变性以及全局鲁棒性，弥补传统滑模控制中趋近阶段不具有鲁棒性的不足[11]。文献[12]利用全局滑模控制，通过设计非线性滑模面对一类不确定非线性系统实现鲁棒控制。文献[13]则针对存在参数变化和外部扰动的导弹伺服系统设计全局滑模控制器，并结合最优线性状态反馈控制器，使系统具有高精度和强鲁棒性的同时实现对系统不确定性的有效补偿。文献[14]设计一种指数函数形式的全局滑模函数对MEMS陀螺仪进行跟踪控制，滑模面虽能快速收敛到零，但在初始阶段存在明显偏差，系统鲁棒性无法保证。针对慢变子系统中存在参数不确定性和有界干扰的情况，本文提出一种改进的全局滑模函数，将分段多项式函数和指数函数相结合，加快跟踪速度，实现全局鲁棒的关节轨迹跟踪。为抑制滑模控制策略所产生的抖振现象，常用方法有趋近率法[15]、干扰观测器法[16]和动态滑模法[17]等。本文采用滤波法[18]，即在滑模控制器输出端加入低通滤波器，可消除未建模动态造成的抖振，且设计简便，易于实现。平滑的控制力矩也保证了慢变子系统在跟踪期望轨迹的同时，尽可能减小对柔性振动的影响。

文献[19]针对3-PRR并联柔性机械臂的轨迹跟踪与振动抑制问题进行研究，采用应变率反馈(Strain Rate Feedback,SRF)控制有效地制了柔性振动。文献[20]采用线性观测器对柔性模态进行估计，并结合LQR(Linear Quadratic Regulator)方法，对柔性振动进行抑制。上述方案虽能抑制柔性振动，但均未考虑柔性振动的外界扰动，不符合工程实际，会对精确控制带来误差。扩张状态观测器(Extended State Observer, ESO)可将系统包含的非线性动态、系统不确定性以及外部干扰等当作可观测的扩张状态，无需具体的扰动模型，是一种通用的扰动观测器。本文在描述系统柔性振动的快变子系统中采用ESO对不易测量的柔性模态坐标导数和不确定扰动进行估计，并结合最优控制理论，对柔性振动进行抑制。最后通过仿真实验证明所设计的组合控制器具有全局鲁棒、快速收敛和零稳态误差等优点。

1 系统动力学建模

不失一般性，考虑做平面运动的FFFSR系统的结构见图1[21]。设系统由自由漂浮的载体B0、刚性杆B1和柔性杆B2组成。建立各分体的主轴连体坐标系(Oi-xiyi)，其中O0与B0的质心OC0重合，O1为连接B1与B0的转动中心，x0为杆B1的对称轴。同时在O2建立坐标系(O2-x2y2)，x2与未变形前的轴线一致。设O1在x0轴上与O0的距离为a0，B1的质心OC1与O1在x1轴上的距离为a1，Bi(i=1,2)的长度为l1，w(x2,t)为B2在t时刻x2(0≤x2≤l2)点处的横向弹性形变。Bi(i=0,1)的质量和转动惯量分别为mi，Ii(i=0,1)柔性杆B2的均匀质量密度和弯曲刚度分别为ρ和EI。Oc为系统的总质心，M=m0+m1+ρl2为系统的总质量。

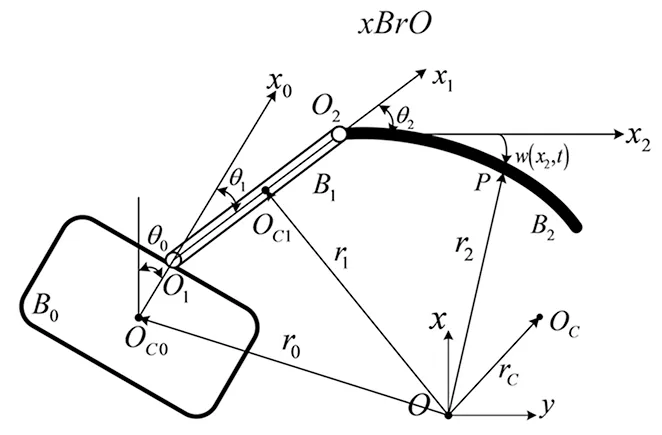
图1 FFFSR系统

建立平动的惯性坐标系(O-xy)，设各分体在垂直于转轴的平面内运动。θ0、θ1和θ2分别表示系统载体姿态及机械臂各个关节的相对转角。质心OCi(i=0,1)相对于惯性坐标系原点O的矢径为ri，r2为B2上坐标x2(0≤x2≤l2)点处的矢径。

由于柔性杆B2在运动过程中必然会发生形变，考虑到B2的长度比其截面半径大的多，故可忽略其轴向形变和剪切形变的影响，仅考虑其弯曲形变，可将其视为EULER-BERNOULLI梁处理。由弹性振动理论可知，柔性杆B2的弹性形变w(x2,t)可用如下的截断模态方程描述：

(1)

式中：φi(x2)(i=1,2,…,n)为柔性杆第i阶的模态函数，ηi(t)为φi(x2)对应的模态坐标，n为截断项数。由于低阶模态对柔性杆振动幅值影响较大，在尽可能不影响精度的情况下简化计算，采用二阶截断模态，即取n=2进行分析。

综合考虑系统的基座和刚性杆件动能Ti(i=0,1)以及柔性杆件动能T2，系统总动能为：

(2)

系统的弹性势能V，即柔性杆的弹性势能为：

(3)

式中：w″(x2,t)为w(x2,t)关于x2的二阶偏导数。

忽略微重力梯度，由拉格朗日第二类方程和动量守恒原理可得到，基座位置、姿态均不受控的自由漂浮柔性空间机器人欠驱动形式的系统动力学方程为：

(4)

2 奇异摄动分解

本节利用奇异摄动法，将FFFSR系统降阶分解为两种时间尺度下的关节轨迹跟踪控制慢变子系统和柔性振动抑制快变子系统。

将式(4)写成分块矩阵形式：

(5)

(6)

(7a)

(7b)

由于系统主要的控制目标是设计控制输入τ使得机械臂关节能准确地追踪期望轨迹并使部分解耦系统(式(7b))的振动得到抑制，因此该控制输入τ可分解为两个部分：

τ=τs(θ)+τf(η)

(8)

式中：τs(θ)为慢变控制部分;τf(η)为快变控制部分。由式(7a)和式(7b)知，关节轨迹跟踪和柔性振动抑制仅通过控制输入τ耦合。一般来说，适当地选择控制输入τ可以达到关节跟踪期望轨迹的预期控制效果，然而仅通过期望轨迹来选择控制输入并不能保证耦合振动模态的动力学系统稳定。故选择奇异摄动法来同时实现关节轨迹跟踪和柔性振动抑制。

令ε=0，并代入式(7b)可得：

(9)

式中:带下标S的向量表示其处于慢变子系统中。

将式(9)代入式(7(a))，可得如下形式的柔性空间机器人慢变子系统表达式：

(10)

(11)

引入新的时间尺度σ=t/ε，令ε=0，可得到快变子系统为：

(12)

3 组合控制器设计

组合控制器的设计目的是得到平滑控制力矩τs使关节铰能稳定跟踪期望轨迹，同时获得能有效抑制柔性振动的控制力矩τf。由于使用两种时间尺度，慢、快变子系统的控制力矩τs和τf可在不同的时间尺度内分别进行设计，最终得到同时使关节稳定追踪期望轨迹并能有效抑制柔性振动的控制输入力矩τ。控制系统的整体框图见图2。

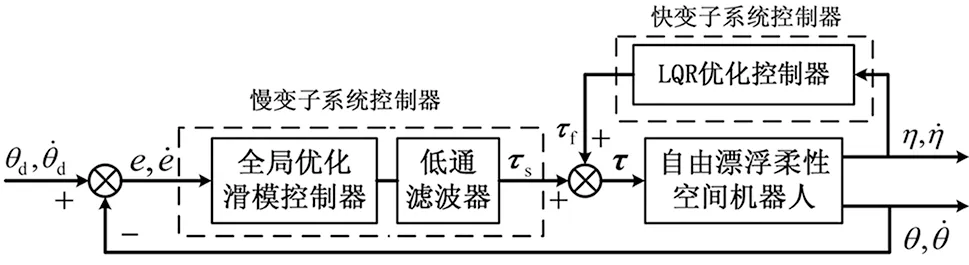
图2 控制系统整体框图

3.1 慢变子系统控制器设计

为使全局滑模控制器输出的控制力矩尽可能平滑，抑制滑模控制策略所产生的抖振现象，在滑模控制器输出端加入低通滤波器(Low-Pass Filter,LPF)，将LPF与系统结合构造虚拟平台，设计虚拟滑模控制律u，见图3。

图3 虚拟控制系统框图

虚拟控制信号u在切换函数的影响下，存在抖振现象，但经LPF将高频抖振控制信号有效滤除后，输出的实际控制信号τ是连续光滑的。实际慢变子系统控制器见图4。

图4 实际控制系统框图

采用如下的LPF形式：

(13)

式中：λi>0。由图4可得：

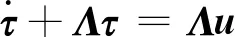
(14)

式中：Λ=diag(λ1,λ2,…,λn),λi>0,i=1,2,…,n。

考虑系统不确定性，自由漂浮柔性空间机器人的慢变子系统动力学方程式(10)可改写为：

(15)

将式(15)代入式(14)得：

(16)

化简后可得：

(17)

设理想的角度指令为θd(t)，则跟踪误差为：

e(t)=θ(t)-θd(t)

(18)

设计滑模面函数为：

(19)

f(t)是为了达到全局滑模而设计的函数，且f(t)满足以下三个条件[11]：

2)当t→∞时，f(t)→0；

3)f(t)的一阶导数存在且有界。

依据上述三个条件，将f(t)设计为：

f(t)=f(0)e-kt

(20)

式(20)满足全局滑模条件，等价于给滑模面函数添加了指数趋近项。由图5可知，f(t)在初始阶段收敛速度过快，对于滑模面函数s(t)的作用并不明显，使得无法完全消除滑模控制的趋近阶段，即无法满足全局鲁棒。

本文在此基础上，提出一种分段多项式函数和指数函数相结合的全局滑模函数形式，其表达式为：

图5 全局滑模函数变化率对比图

定义LYAPUNOV函数为：

(22)

将V对时间求导，可得：

(23)

(24)

(25)

式中：

(26)

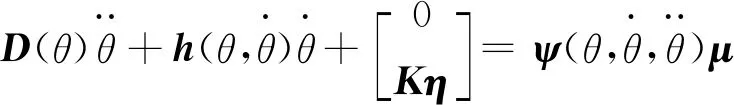
(27)

成立。

根据性质2，H可写为：

(28)

式中：φ为未知向量。存在已知向量φ0，使得：

(29)

式中：εi>0,i=0,1,…,n。则

(30)

设计滑模控制律为：

(31)

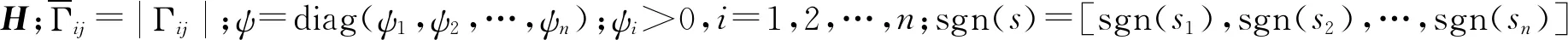
定理1 针对含不确定参数的慢变子系统(15)，存在控制律(31)使得系统输出渐近稳定跟踪期望轨迹，并一致最终有界。

证 将控制律u代入式(30)，进行化简得到：

(32)

(33)

证毕。

为了进一 步减弱抖振的影响，采用饱和函数替代符号函数。将饱和函数设计为：

(34)

式中：δ>0。

u=-Λ-1[Γφ0+κsat(s)]

(35)

3.2 快变子系统控制器设计

为更加精确地进行快变子系统的控制器设计，需考虑柔性振动系统中的不确定部分，式(12)改写为：

(36)

定义快变子系统的输出向量：

(37)

并假定输出变量y可通过测量方式获得。

由于(Af,Bf,C)可控可观，则采用状态观测器估计值形成状态反馈时，其系统的状态反馈设计和观测器设计可分别独立进行。

对系统进行状态反馈设计时，针对标称系统，采用线性二次型调节器(LQR)进行柔性振动抑制，即使系统状态ζ调节到零。以减少柔性振动和控制能量消耗为优化目标，构造如下形式的最优控制性能指标函数：

(38)

式中：Q和R分别为状态向量ζ和控制向量τf1对性能指标影响的相对重要性所占权重。则快变子系统的最优控制为：

(39)

式中：P为下列Riccati方程的解。

(40)

针对控制率中的不确定补偿项τf2取：

τf2=-δ/b

(41)

将τf=τf1+τf2代入式(42)可得：

(42)

采用ESO方法，将δ视为一个扩张状态，在式(36)的基础上得到状态扩张系统为：

(43)

针对系统式(43)设计ESO：

(44)

gi的选择极其关键，目前大多数采用如下带有线性区的非线性函数：

(45)

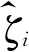
结合式(44)和式(45)，取gi(eo1)=eo1，可得：

(46)

式中：Hk=[β1,β2,β3]为待确定的观测增益向量。

通过式(47)可完成对系统状态的估计，此时快变子系统控制律为：

(47)

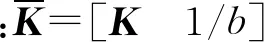
将慢变子系统的全局滑模控制部分τs与快变子系统最优控制部分τf结合，利用式(8)，得到使关节稳定跟踪期望轨迹并能有效抑制柔性振动的控制力矩τ。

4 仿真校验

以图1所示平面FFFST为例，验证所提方法的有效性。系统惯性参数见表1所示。

B2杆单位长度的密度为ρ=1 kg/m，均匀弯曲刚度为EI=200 Pa。仿真时假设柔性空间机器人关节铰的期望运动轨迹为θd(t)=[costcost](rad)，初始角度为θ0=[0 0](rad)，柔性杆的初始、期望模态坐标均为η0=ηd=[0,0](m)。选取慢变子系统控制参数κ=diag(6,5,5)，LPF参数Λ=diag(25,25,25)，滑模面参数Λ1=diag(5,5,5),Λ2=diag(50,50,50)，全局滑模函数参数T=1.1 s，k=7.9，不确定部分τd=[0.2sint0.15cost](rad)。

选取快变子系统权值阵Q(ζ)=104×diag{8,8,8,8}，R(ζ)=10-1×diag{2,2}，观测器参数β1=β2=100，β3=200，μ1=μ2=μ3=0.5，α=0.01，不确定扰动δ=[0.001sint0.001cost](rad)。仿真时间为10.0 s。仿真结果见图6～图15，其中图6～图12为关节轨迹跟踪仿真结果；图13～图15为柔性振动抑制仿真结果。

图6 改进前关节位置跟踪轨迹图Fig.6 The comparison between the desired angular position and the actual one before improved

表1 空间机器人模型惯性参数

图7 改进后关节位置跟踪轨迹图

图6、图7分别为全局滑模函数f(t)改进前后，关节铰位置跟踪轨迹图，表明采用基于低通滤波器的全局滑模控制器能够克服不确定性的影响，实际轨迹均能稳定跟踪期望轨迹，但改进f(t)后跟踪速度明显加快。

图8、图9分别表示全局滑模函数f(t)改进前后s函数的变化。不难发现，改进前后s函数均能快速趋近滑模面，在零值附近微小波动，但改进前s函数在初始阶段存在较大偏差，鲁棒性无法保证；而改进后s函数波动范围更小，鲁棒性更强。

图8 改进前s函数变化图

图9 改进后s函数变化图

图10为f(t)改进前后关节铰位置跟踪轨迹误差对比图。对比图6～图9，说明全局滑模函数f(t)改进后关节轨迹跟踪误差收敛速度明显加快，滑动模态运动更加稳定，具有更强的鲁棒性。

图10 关节跟踪轨迹误差对比图

图11、图12为改进f(t)后，LPF滤波前后关节铰的控制力矩，即虚拟控制力矩和实际控制力矩。表明经LPF滤除高频控制信号后的实际控制力矩有效抑制了抖振，在保证关节轨迹跟踪精度的同时，尽可能减小了对柔性杆件的影响。

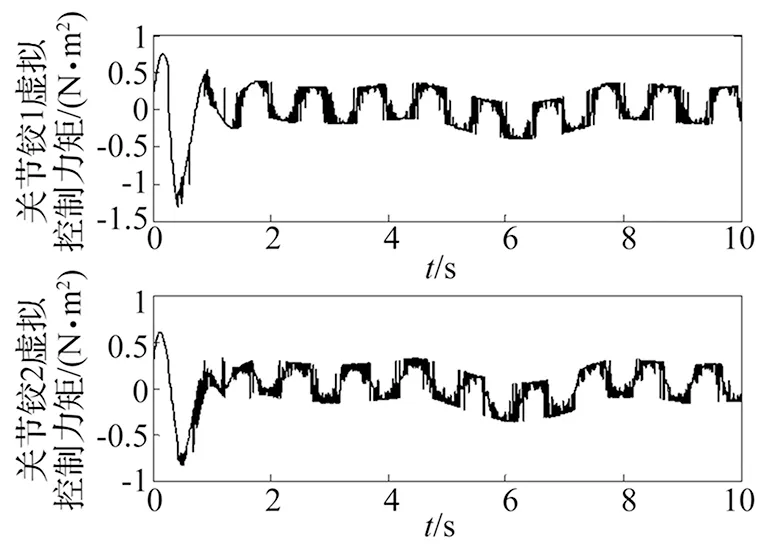
图11 虚拟控制力矩

图12 实际控制力矩

图13以柔性杆一阶振动模态为例，在未经过柔性振动主动抑制的情况下，对比虚拟和实际力矩控制下的模态坐标。不难发现，实际力矩控制下的模态坐标收敛速度更快，以更小振动幅值趋于稳态，说明经LPF滤波后的实际控制力矩对柔性振动的影响更小。

图13 不同力矩下模态对比图

图14 未主动抑制柔性模态

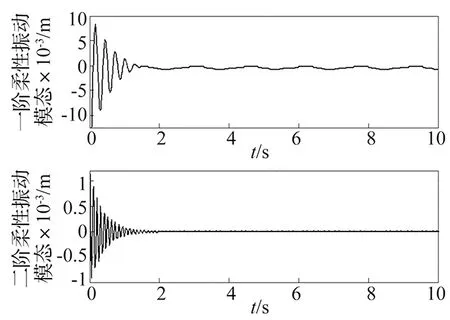
图15 主动抑制柔性模态

图14、图15分别为未经过主动抑制和主动抑制后的柔性振动一、二阶模态。不难发现，经主动抑制后的柔性振动模态幅值减小，收敛迅速，说明基于ESO的振动抑制优化控制器能够对柔性振动进行有效抑制。

5 结 论

对于存在参数不确定性与有界干扰的自由漂浮柔性空间机器人系统，本文利用奇异摄动法提出了一种基于低通滤波器的改进全局滑模关节轨迹跟踪控制器和基于ESO的振动抑制优化控器相结合的组合控制器设计方法，实现了关节轨迹的稳定跟踪和对柔性振动的有效抑制。理论推导和仿真分析表明：

(1)引入低通滤波器对高频控制信号进行有效滤除，消除滑模控制的抖振现象，使关节在跟踪期望轨迹的同时对柔性振动带来尽可能小的影响；

(2)提出一种分段多项式函数与指数函数相结合的全局滑模函数形式，加快关节跟踪速度，并保证响应全程具有鲁棒性，克服不确定性的影响；

(3)引入ESO对不易测量的柔性振动模态坐标导数和未知扰动进行估计，避免测量噪声的干扰以及不确定干扰，更贴合工程实际，有效抑制了柔性振动。

[ 1 ] JUNFENG L, ZHAOLIN W. Study on attitude dynamics of a liquid filled spacecraft with manipulator[J]. Journal of Astronautics, 1999, 20(2): 81-86.

[ 2 ] ANGEL O M. A review of space robotics technologies for on-orbit servicing [J]. Progress in Aerospace Sciences,2014,68(1):1-26.

[ 3 ] 刘正雄, 黄攀峰. 基于递推差分进化算法的空间机器人参数辨识[J]. 宇航学报,2014, 35(10): 1127-1134. LIU Zhengxiong, HUANG Panfeng. Parameter identification of space robot based on recursive different evolution algorithm[J]. Journal of Astronautics, 2014, 35(10): 1127-1134.

[ 4 ] 洪在地, 贠超, 陈力. 漂浮基空间机器人及其柔性影响下逆模神经网络控制[J]. 宇航学报, 2007, 28(6):1510-1514. HONG Zaidi, YUN Chao, CHEN Li. Inverse-model neuro-control of free-floating space robot with rigid manipulators and rigid-flexible manipulators[J]. Journal of Astronautics, 2007, 28(6): 1510-1514.

[ 5 ] HU Q, XU L, ZHANG A. Adaptive backstepping trajectory tracking control of robot manipulator[J]. Journal of the Franklin Institute, 2012, 349(3): 1087-1105.

[ 6 ] 谢箭, 刘国良, 颜世佐,等. 基于神经网络的不确定性空间机器人自适应控制方法研究[J]. 宇航学报, 2010,31(1):123-129. XIE Jian, LIU Guoliang, YAN Shizuo, et al. Study on neural network adaptive control method for uncertain space manipulator[J].Journal of Astronautics, 2010, 31(1): 123-129.

[ 7 ] WANG M, LI Y, REN X. Adaptive sliding mode control for hydraulic flexible manipulator based on two-parameter singular perturbation method[C]//Intelligent Human-Machine Systems and Cybernetics (IHMSC), 5th, International Conference on. IEEE, 2013, 2: 57-60.

[ 8 ] ZENG P L, WANG S X, QIU J J, et al. Flexible manipulator control based on singular perturbation theory study[C]//Applied Mechanics and Materials,2013, 346: 69-73.

[ 9 ] 翟光, 张景瑞, 周志成．静止轨道卫星在轨延寿技术研究进展[J]. 宇航学报, 2012, 33(7):122-134. ZHAI Guang, ZHANG Jingrui, ZHOU Zhicheng. A review of on-orbit life-time extension technologies for GEO satellites[J]. Journal of Astronautics, 2012, 33(7): 122-134.

[10] 石苏忠, 王永智. 基于多项式插值的自由漂浮空间机器人轨迹规划粒子群优化算法[J].宇航学报,2011, 32(7):1516-1521. SHI Suzhong, WANG Yongzhi. A polynomial interpolation based particle swarm optimization algorithm for trajectory planning of free-floating space robot [J]. Journal of Astronautics, 2011,32(7):1516-1521.

[11] LU Y S, CHEN J S. Design of a global sliding-mode controller for a motor drive with bounded control[J]. International Journal of Control, 1994,62(5):1001-1019.

[12] MOBAYEN S. An LMI-based robust controller design using global nonlinear sliding surfaces and application to chaotic systems[J]. Nonlinear Dynamics, 2014, 79(2): 1075-1084.

[13] LIU X, WU Y, DENG Y, et al. A global sliding mode controller for missile electromechanical actuator servo system[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(7): 1095-1104.

[14] CHU Y, FEI J. Adaptive global sliding mode control for MEMS gyroscope using RBF neural network[J]. Mathematical Problems in Engineering, 2015,2015: 1-9.

[15] FALLAHA C J, SAAD M, KANAAN H Y, et al. Sliding-mode robot control with exponential reaching law[J]. Industrial Electronics, IEEE Transactions on, 2011, 58(2): 600-610.

[16] YANG J, LI S, YU X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J]. Industrial Electronics, IEEE Transactions on, 2013, 60(1): 160-169.

[17] YANG J, SU J, LI S, et al. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach[J]. Industrial Informatics, IEEE Transactions on, 2014, 10(1): 604-614.

[18] ZHAO D, LI C, ZHU Q. Low-pass-filter-based position synchronization sliding mode control for multiple robotic manipulator systems[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2011, 225(8): 1136-1148.

[19] ZHANG Q, MILLS J K, CLEGHORN W L, et al. Trajectory tracking and vibration suppression of a 3-PRR parallel manipulator with flexible links[J]. Multibody System Dynamics, 2015, 33(1): 27-60.

[20] 杨明, 董晨, 王松艳,等. 基于有限时间输出反馈的线性扩张状态观测器[J].自动化学报, 2015, 41(1):59-66. YANG Ming, DONG Chen, WANG Songyan, et al. Linear extended state observer based on finite-time output feedback[J]. Acta Automatica Sinica, 2015, 41(1):59-66.

[21] 于潇雁, 陈力. 参数不确定与有界干扰自由漂浮柔性空间机械臂基于速度观测器的奇异摄动鲁棒控制及振动抑制[J].振动与冲击, 2015, 34(14): 85-92. YU Xiaoyan, CHEN Li. Velocity observer based singular perturbation robust control and vibration suppression for a free-floating space flexible manipulator with unknow payload parameters and bounded disturbances[J]. Journal of Vibration and Shock, 2015,34(14):85-92.

[22] GAO Z Q. Scaling and bangwidth-parameterization based controller tuning.[C]//Proceedings of the American Control Conference, 2006,6: 4989-4996.

Global sliding mode tracking control and ESO vibration suppression for a FFFSR based on singular perturbation method

PANG Zhenan1, ZHANG Guoliang1, YANG Fan1,2, WU Ge1, CHEN Zhikan1

(1.The Second Artillery Engineering University, Xi’an 710025, China；2. Baoji New High Tech Research Institute, Baoji 721000, China)

Joints trajectory tracking control and flexible vibration active suppression techniques for a free-floating flexible space robot (FFFSR) were discussed under parameter uncertainties and bounded disturbance. A composite controller containing a slow control subsystem for joints trajectory tracking control and a fast control subsystem for describing flexible vibration was proposed using the singular perturbation method. In the slow subsystem, an improved global sliding mode function with a low-pass filter to suppress sliding mode chattering was designed to achieve global robust and fast convergence of joints trajectory tracking. The fast subsystem adopted an extended state observer (ESO) to estimate coordinate derivatives of flexible modes and uncertain disturbance measured hardly, and used LQR method to suppress the flexible vibration. Numerical simulation results demonstrated the feasibility and effectiveness of the proposed control strategy.

free-floating flexible space robot (FFFSR); singular perturbation method; global sliding mode control (GSMC); low-pass filter (LPF); extended state observer (ESO); uncertainty

中国工程院与国家自然科学基金委联合资助(2014-zcq-10)

2016-01-13 修改稿收到日期：2016-03-20

庞哲楠 男，硕士，1992年生

张国良 男，博士，教授，1970年生

TP242