如何做实证：调查研究

喻 平

（南京师范大学课程与教学研究所 210097）

调查研究是通过对原始材料的观察，有目的、有计划地搜集研究对象的材料从而形成科学认识的一种研究方法.[1]调查研究是一种描述性研究，即对研究对象进行客观描述而不采用人为的干预手段.调查研究主要包括问卷调查和访谈调查，从技术层面说，问卷调查设计难度高于访谈调查，本文讨论问卷调查方法.

1 问卷调查的基本类型

从调查问题的性质来看，可以分为“事实性问题调查”和“态度性问题调查”.[2]事实性问题的调查，是通过调查了解一些基本性事实，包括被试过去和现实的一些实际行为.例如，每天作业完成情况，上课发言情况等.态度性问题的调查，是要了解被试对某个问题的看法和认识，以及个人的认识倾向.当然也包括有关价值和人格方面的观念（这类问题我们将在另文中讨论）.

从调查的目的来看，可以分为“分类性调查”和“倾向性调查”.分类性调查是按被试所持不同观点进行群体分类，即把持有相同观点的被试合为一类，持不同观点的被试分门别类.分类性调查的题目类型可以是封闭性问题，题目的选项可以是单选也可以是多选，最后通过选项人数的百分比统计数据；也可以是开放性问题，根据被试回答作编码分类统计数据.倾向性调查是指通过调查反映被试对一个对象、观念、行为的认可程度.倾向性调查一般采用利克特量表，给4个或5个选项赋值，最后把每题所得分数相加即为问卷得分.

一般说来，一份问卷最好独立地设计为分类性调查或者倾向性调查，这样便于数据统计和分析.其实，许多选项既可以分类统计，也可以赋值用分数统计.如果可以赋值，可选用赋值方法，这样便于对问卷的结构作分析，同时给最后的数据统计带来方便.当然，也可以在一份问卷中将两种设计合为一体，此时数据收集和统计分析要分别处理.

2 调查问卷的设计

如上所述，两种类型的调查有差异，因此分别讨论.

2.1 分类性调查问卷设计

分类性调查问卷设计的步骤如下图1.

图1 分类性问卷设计的步骤

第一，概念界定.概念界定是指对所研究问题中涉及的概念作出准确描述.概念界定有两种方式：内涵式界定和外延式界定.内涵式界定是通过对概念本质属性的描述来揭示概念的内涵；外延式界定是指出概念包括的范围.一些大家公认的概念不必自己再去作新的界定，否则容易引起混乱.

例如，研究课题是：中学生数学阅读的现状调查.这个课题中，要对数学阅读作出界定.内涵式界定为：数学阅读是指对数学材料的阅读，阅读包括内化、理解、推理和监控的心理过程.内化是指个体将外部信息转化为内部信息的过程，主要包括对信息的选择性编码和语言互译；理解是对材料从局部到整体的加工过程；数学材料的阅读总是伴随着推理；而反省贯穿整个阅读活动，主要表现为自我提问.外延式界定：数学阅读的内容，一般包括对教材的阅读、问题解决中对题目的阅读以及课外数学材料的阅读.显然，外延式界定事实上给出了问题研究的范围和边界.

第二，提出假设.提出假设的本质是明确研究的目的，它既是研究的起点又是研究归宿.在上例中，可以提出假设：①目前中学生数学阅读水平不高；②不同年级学生的阅读水平存在差异；…….

第三，确定维度.一份问卷应当有清晰的维度，要思考调查的内容应当包括哪几个方面，这些方面是否概括了研究的内容，是否能够达到研究的目标.这样的梳理不仅使问卷条理清楚，而且不同维度提供的数据也能够充分得到利用，使研究更加细致深入.

案例1“中学生数学阅读研究”的一种分解.

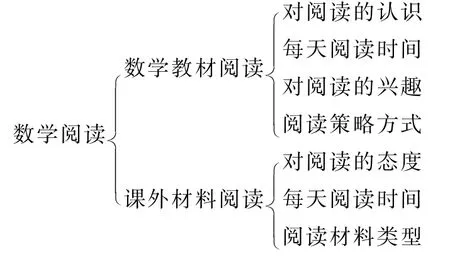
对一个研究问题维度的确定方式不是唯一的，相当于分类的标准不同会得到不同的分类一样.这主要受到研究者价值观、学术观的影响.但是必须注意，划分维度不是一种随意的行为，应当有一定的理论依据或者是对前人研究成果改造而得.

第四，编拟题项.根据已经分好的维度，在每一个维度上设计若干问题，每个维度设计的题目数量可以不同.

案例2两道数学阅读分类调查题目举例.

（1）平均而言，你每天阅读数学教材的时间是（ ）

A0分钟…………B1～10分钟

C11～20分钟 D21分钟以上

（2）在阅读数学教材时，你采用的方式是（ ）

A会找出教材的重点和难点

B提前阅读第二天要学习的教学内容

C上完课后阅读当天学习过的教材内容

D阅读完一段教材后我会马上做相关题目

这两个题目分别反映被试“每天阅读时间”和“阅读策略方式”两个维度的情况.（1）是单项选择，（2）是多项选择.数据收集是统计每个选项的百分比，以反映每一类人数的百分比，同时可以对不同群体作差异性检验.

在题型上，可以考虑增加几道开放性问题，作为对封闭性问题的补充.例如：你认为数学阅读对学习有哪些好处？你觉得阅读数学教材的困难之处在什么地方？

2.2 倾向性调查问卷设计

倾向性调查问卷设计的步骤如下图2.

图2 倾向性问卷设计的步骤

图2中，前面四步与分类性调查相同.倾向性问卷多是采用利克特量表，单项选择，因此在编制题目时要考虑对每一个选项赋值.

案例3“数学教材阅读”维度的5个题项.

（1）数学阅读对数学学习有直接影响（ ）

A完全同意 B比较同意 C一半同意

D不太同意 E完全不同意

（2）我觉得数学教材应当每天阅读（ ）

A完全同意 B比较同意 C一半同意

D不太同意 E完全不同意

（3）我感觉阅读数学教材很枯燥、无味（ ）

A完全同意 B比较同意 C一半同意

D不太同意 E完全不同意

（4）在阅读教材时，我总是会找出阅读的难点和重点（ ）

A完全同意 B比较同意 C一半同意

D不太同意 E完全不同意

（5）在阅读教材时，我很难把握阅读内容中的关键词（ ）

A完全同意 B比较同意 C一半同意

D不太同意 E完全不同意

其中，（1）、（2）、（4）题正向计分5、4、3、2、1；（3）、（5）题反向计分1、2、3、4、5.

第五，样本预测.选择小样本进行问卷预测，收集数据.

第六，计算信度.信度是对测量一致性程度的估计.可定义为一组测验分数中真分数的方差与实测分数的方差的比率.计算信度一般用下面几种方法：

（1）重测信度：也称稳定系数，用同一问卷对一组被试进行两次测试（两次测试间隔一段时间），两次测验分数的相关系数.计算公式为：

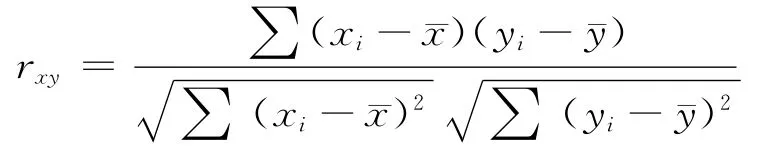
其中xi，yi分别表示每一个被试两次测试的成绩，分别表示两次测试的平均分.

（2）分半信度：把一份测验按题目的奇偶顺序或其他方法分成尽可能平行的半份测验，然后计算两半之间得分的相关系数.由于这种方法可能低估原长测验的信度，所以需要用斯皮尔曼-布朗公式（略）进行修正.

（3）克伦巴赫α系数：是分半信度的推广，是把同一套题分成多部分，多个部分之间的一致性程度.

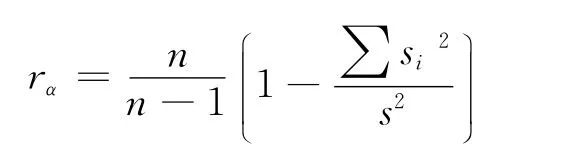
其中n表示子量表的题项数，si为各子量表的标准差，s2为测样总方差.要计算每一个维度的α系数，再计算全问卷的α系数.

第七，修订问卷.假定在计算某一维度的α系数时，发现系数值大于0.4，则维度的全部题目可以保留；如果系数值小于0.4，则可对每一个维度采用依次删除一个题目分别进行信度计算，即删除第1题，计算剩余题项的α系数，记为α1，然后放加第1题，删除第2题，计算α系数，得到α2，以此类推，比较α，α1，α2，……，找出最大的αi.保证删除题目后的信度大于0.4即可认为这个维度合理.同样，计算总问卷时也可采用这个方法，最后得到信度较高的问卷作为修订后的问卷.

3 使用SPSS软件作数据处理

调查问卷需要处理的数据，第一，如果是采用对问卷选项赋值的利克特量表，就应当计算问卷的信度；第二，对于问卷结果用百分比统计的数据，如果要对不同群体的选项百分比作比较，就需要进行百分比的差异性检验，采用的方法是χ2检验；第三，对于用利克特量表统计的分数，如果要对不同群体的调查结果分数作比较，就要对不同群体的分数作t检验.这些数据处理都可以用SPSS统计软件完成，下面分别介绍.

需要说明的是，下面的计算只用了小样本数据以说明操作步骤，在真实的研究中，需要的样本量应更大.一般说来，样本量≥30方能作统计检验.

3.1 问卷的克伦巴赫α系数/分半信度计算

案例4以案例3的问卷为例，用SPSS软件计算“数学教材阅读”维度的克伦巴赫a系数.

假定表1是A校24个被试在5个题项上的得分，一个题项对应一个变量，用X1到X5表示.

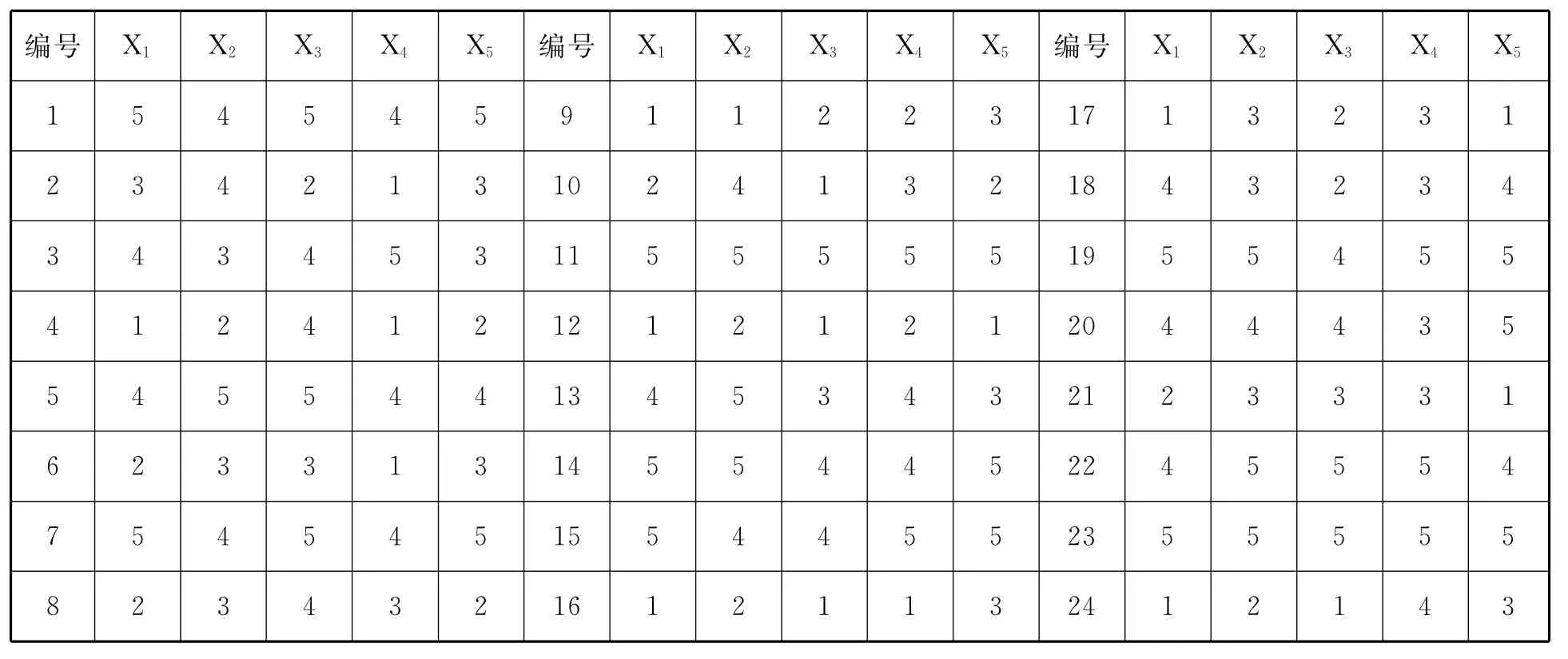
表1 A校24个被试在“数学教材阅读”维度得分

打开SPSS软件，显示SPSS页面.按照下面程序操作：

（1）点击[变量视图]，在第一列“名称”中每一行中依次输入变量X1，X2，X3，X4，X5.（后面的类型、宽度……等数据会自动生成）

（2）点击[数据视图]，输入数据.

（3）依次点击[分析]、[度量]、[可靠性分析]，弹出〈可靠性分析〉对话框.

（4）点击[中间键]，将左边X1到X5送入右边〈项目〉栏.

（5）点击[统计量]，在打开的〈可靠性分析：统计量〉对话框中，在〈描述性〉中选择“项”（输出各题的平均分、标准差）、“度量”（输出量表总分的平均分、标准差）.点击[继续]返回.

（6）点击[确定]，输出α系数.如果要计算分半信度，在〈可靠性分析〉对话框内的〈模型〉中选项“分半”.

本题输出结果如下：

表2 可靠性统计量

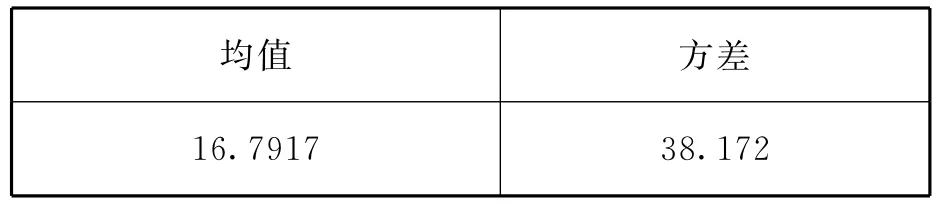
表3 标度统计量

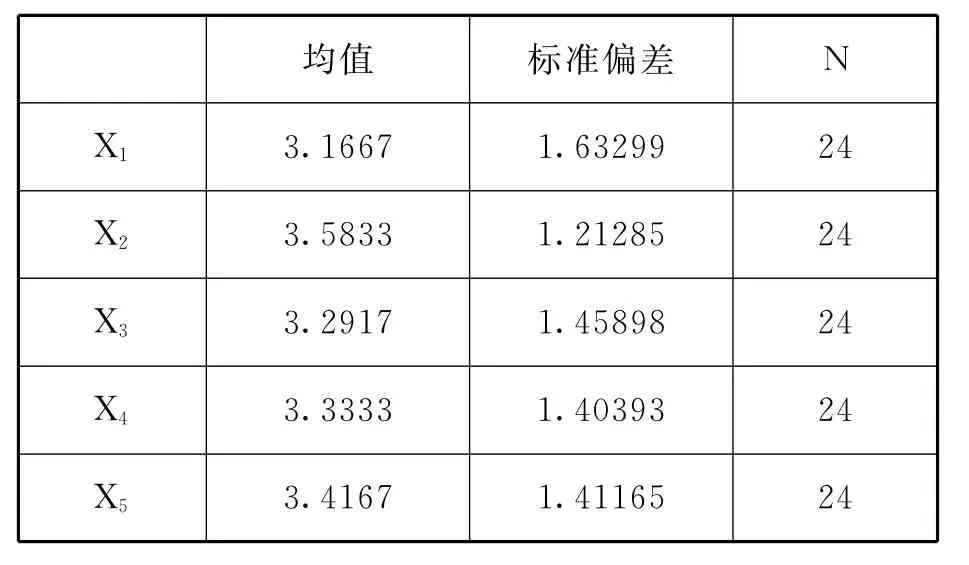
表4 项统计量

从表2中可以看到，α系数为0.915，表明内部一致性系数高，这个分量表有很好的信度.

3.2 选项百分比的χ2检验

问卷测试完后，可以就不同群体在每一个题目上选项情况进行差异性比较.

在案例3的5个题项中，我们不对每个选项赋值，而是作分类处理，即统计的数据只是反映在每个选项上人数的百分比.假定有两个学校的学生参加调查，于是想比较这两所学校的调查数据是否存在差异，此时需采用χ2检验.

下面以表1为例，X1是案例3中的第（1）题，原来赋值为5、4、3、2、1，对应的选项为A、B、C、D、E，我们还是用编码5、4、3、2、1对应表示这五个选项而不是赋值.表1第2列给出了A校24个被试在第（1）题上的选项数据，假设B校选择30名被试，在5道题目上的选项见表5.现在要检验两校学生在第（1）题上选项是否存在差异.

案例5对A校和B校的学生进行数学阅读问卷调查，在A校选取24名被试，B校选取30名被试，他们在“数学教材阅读”维度第（1）题的选项情况如表1和表5中的变量X1.问两组被试在该题的选项百分比是否存在差异？

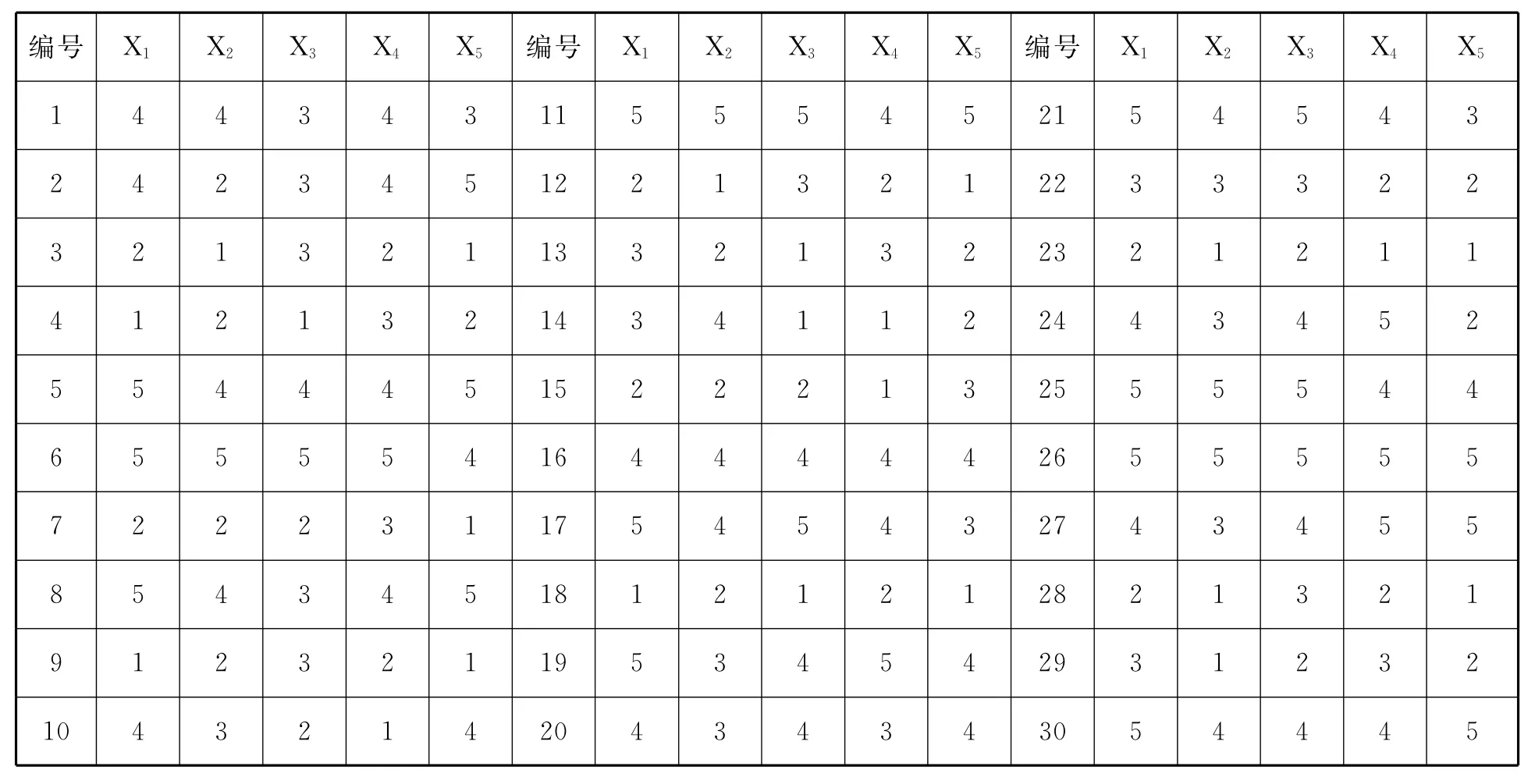
表5 B校30个被试在“数学教材阅读”维度得分

SPSS计算步骤：

（1）点击[变量视图]，在第一行第一列输入“分组”（定义分组变量）.在第二行第一列输入“X”（定义数据变量）.

（2）点击[数据视图]，在“分组”一列中，输入24个1（A校样本数），接着输入30个2（B校样本数）.在数据变量“X”一列中，输入对应数据.

（3）依次单击[分析]、[描述统计]、[交叉表]，弹出〈交叉表〉对话框.

（4）点击[中间按钮]，将变量X放入〈行（S）〉中，分组变量放入〈列（C）〉栏中.

（5）点击[统计量]，选择“卡方（H）”. 点击[继续]，回到〈交叉表〉.点击[单元格]，弹出〈交叉表：单元显示〉对话框，选择“观察值（O）”“期望值（E）”“列（R）”“行（C）”“总计调节的标准化（A）”，点击[继续]，回到〈交叉表〉对话框.

（6）在〈检验类型〉选项栏中任选择一种.

（7）点击[确定]，输出结果.

计算的结果如表6（交叉表省略）.

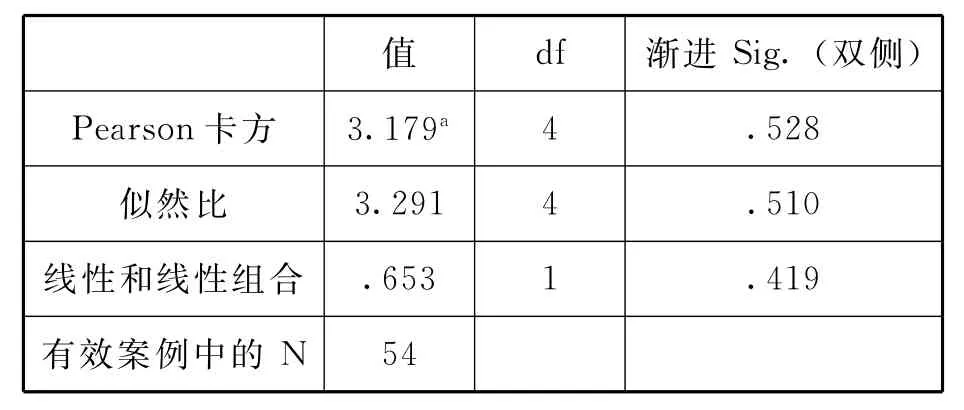
表6 卡方检验结果

表6为百分比同质性卡方检验，卡方值为3.17 9，自由度为4，显著性概率值p=0.52 8＞0.05，未达到0.05显著性水平，表明两个学校被试在第（1）题5个选项选择次数百分比间没有显著性差异.

3.3 两个不同群体问卷得分的差异性检验

问卷用利克特量表计分，最后可以求出每个被试的问卷总分.在研究问题时，我们有时希望对不同的群体的平均分作比较，这种情形在统计学上可以作t检验（三个组及以上作比较要用方差分析）.下面以表1和表5的数据为例（现在以计分方式统计而不是以选项统计），检验A、B两所学校学生在数学教材阅读方面的差异.

打开SPSS页面，

（1）点击[变量视图]，定义自变量“学校”，依次定义数据变量“a，b，c，d，e，总分”（a，b，c，d，e，是在5个选项A、B、C、D、E的数据）.

（2）点击[数据视图]，输入两组数据.“学校”的数据为1，2.在第一列上输入数字1，1的个数是第一组样本数；接着输入数字2，2的个数是第二组样本数.

（3）依次点击[分析]、[比较均值]、[独立样本T检验]，弹出〈独立样本T检验〉对话框.

（4）点击[中间键]，将检验变量“a，b，c，d，e，总分”送入右边上半部分的〈检验变量（T）〉框中.将分组变量“学校”送入右边下半部分的〈分组变量（G）〉小框中.

（5）选择“学校”，点击[定义组]，弹出〈定义组〉对话框.在其下第一个小白框中输入数值1，在第二个小白框中输入数值2，然后点击[继续]，返回主对话框.

（6）点击[确定]，即得结果.

（7）观察“方差方程的Levene检验”中的Sig（第3列），若Sig＞0.05，则方差没有差异，即方差相等，此时选择假设方差相等一行的数据作为检验结果，即观察“均值方程的t检验”Sig的值（第6列）；若第3列Sig＜0.05，则方差有差异，即方差不相等，此时选择假设方差不相等一行的数据作为检验结果.

结果如下（组统计量表省略）：

表7 A校与B校独立样本T检验

从表7中可以看到，在各选项上，“方差方程的Levene检验”中Sig的值均大于0.05，因此方差相等，再看“均值方程的t检验”中Sig的值，这些值均大于0.05，因此两个学校的学生在各个选项及总分上均不存在显著性差异.