灰色系统与BP神经网络组合模型及其应用

杨世娟，卢维学，方辉平（黄山学院 数学与统计学院，安徽黄山245041）

灰色系统与BP神经网络组合模型及其应用

杨世娟，卢维学，方辉平
（黄山学院 数学与统计学院，安徽黄山245041）

影响财政收入的因素有很多，各因素之间信息重叠的现象较严重，文章通过逐步回归选择了影响财政收入的几个显著因素。又鉴于灰色系统对小样本数据预测的优良特性，对每个选定的影响因素建立灰色预测GM(1，1)模型，得到各因素2015年、2016年的预测值。运用BP神经网络模型对1995—2014年数据进行训练，将灰色预测得到的预测值代入训练好的网络中，预测出2015年、2016年的安徽省的财政收入。

逐步回归；灰色预测GM(1，1)；BP神经网络模型

0 引言

财政收入的有效预测是加强宏观经济管理和提高决策水平的前提与基础。且财政收入会受一般收入、政府性基金收入、经济发展状况、政府的相关政策以及征收管理等众多因素的影响,因此要想科学有效地预测财政收入，就必须综合考虑各种影响因素，建立科学的预测体系。

鉴于灰色模型在小样本量数据预测中的优势，本文采用灰色预测模型对样本的数量进行扩张，再基于BP神经网络对数据进行训练、测试，预测出2015年、2016年的安徽省的财政收入，以供相应部门进行分析、决策。

1 模型方法

1．1 灰色GM(1，1)模型

GM(1，1)具体步骤如下：

（1）累加生成

将原始数据X(0)=(x(0)(1)，x(0)(2)，…,x(0)(n))通过一阶累加生成得到新的序列：

X(1)=(x(1)(1)，x(1)(2)，…,x(1)(n))，其中，

（2）灰导数与近邻均值生成序列

x(1)的灰导数为：

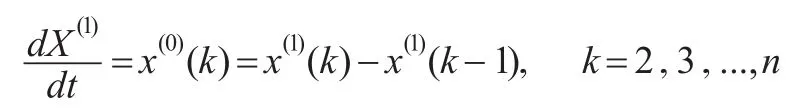
定义近邻均值生成序列：

（3）建立灰微分方程

一阶累加生成序列X(1)具有指数增长规律，满足微分方程：

其中，a与b为常数。

得到（2）式的解为：

（4）解白化微分方程

相对于灰微分方程，称（1）式为白化微分方程，其解得结构如下：

还原后的序列值为：

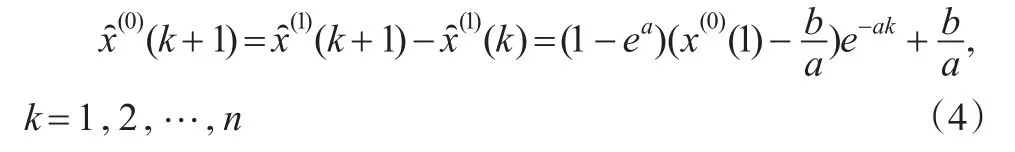
1．2 BP神经网络模型

设BP网络输入层m个神经元，输出层n个神经元，隐层有p个神经元，输入层节点记为d(i)，i=1,2,…,m，隐层节点为d(j)，j=1,2,…,p，输出层节点为d(k)，j=1,2,…,n。xi为d(i)的输入值或输出值，Hj、hj；Yk，yk分别为d(j)、d(k)的输入或者输出，y*k为d(k)的期望输出。d(i)，d(j)、d(j)，d(k)之间的连接权分别记作ωij、ωjk。对于网络隐层，有：

对于网络输出层，有

对此采用tan-sigmoid函数作为BP算法的的转换函数,其特点是将(-∞，+∞)的输入分别映射到区间（-1, 1），其中的输入与输出的关系正好可以反映单个神经元的响应特性，可以有效减少隐层的节点数、加快收敛速度和提高收敛精度。

2 模型检验

2．1 灰色预测模型

灰色预测模型精度的检验一般有三种不同的方法，即残差检验、关联度检验和后验差检验，对此运用残差检验。

计算原始数列 x(0)(k)与模型计算值 x^(0)(k)的残差δ(0)(k)和相对误差M(0)(k)，残差δ(0)(k)=x(0)(k)-x^(0)(k)，相对误差M(0)(k)=δ(0)(k)/x(0)(k)，一般认为M(0)(k)＜0.2时，模型残差检验是合格的。

2．2 BP神经网络模型

BP神经网络训练后的实际输出值与期望值直接的误差E定义如下：

从（10）式知，调整权值可以改变误差E，调整权数的目的是使误差不断减小，则有：Δwjk=-η∂E/∂wjk，Δwij=-η∂E/∂wij其中η∈(0，1)为反映学习速率的常数。

3 实证分析

3．1 数据与指标选择

从1994年开始，我国的财政体制发生了重大改革，开始实行分税制财政体制，影响了财政收入数据的一致性，由此1994年前后的数据是有差异的，而且没有找到合适的方法对前后数据进行量度统一，对此选择安徽省1995—2014年数据。

影响财政收入的因素有很多，在诸多学者研究的基础上，初步选取以下变量为影响因素：税收收入X1、非税收收入X2、地区生产总值X3、第一产业生产总值X4、第二产业生产总值X5、第三产业生产总值X6、全社会固定资产投资X7、就业人数X8、居民消费水平X9、城镇居民人均可支配收入X10。

（1）相关分析

在定量数据预测过程中，相关系数可以用来描述变量之间的关系，可以初步判断因变量与各个解释变量之间的线性关系是否存在。如表1所示。

表1 财政收入及影响因子之间的相关系数

由表1发现，各变量与财政收入线性关系显著，且呈现高度正相关关系，即所有变量暂时保留。由于各个影响因素之间都是高度相关，违背了回归分析的基本假设，会导致一系列的错误，模型不通过。对此下面进行逐步回归进行变量选择。

（2）基于逐步回归的变量选取

自变量的选择涉及的计算量比较大，且过程繁琐，利用逐步回归法建立不同的模型，依据每个回归系数的 p值，逐个剔除不显著变量，直到模型中的指标变量都是影响预测对象的显著因素为止。经过检验，通过检验的模型结果如表2所示。

表2 财政收入与各个影响因素的逐步回归结果

由表2的结论，在逐步回归过程中，变量X2、X3、X6、X7、X8、X9、X10被剔除，综上，预测模型的变量选择为X1、X4、X5。

（3）灰色预测模型

基于灰色预测模型理论，分别构建变量X1、X4、X5的预测模型。以X1为例，有：

利用该模型，可得出原序列拟合值，通过检验发现它们的残差值均比较小，说明模型的精度较高。在此基础上分别对2015年与2016年的变量X1、X4、X5进行预测，预测值与拟合图如表3和图1所示。

表3 各变量2015年与2016年预测值

图1 X1、X4、X5预测值与真实值对比图

3．2 BP神经网络模型

由于BP神经网络可以任意逼近非线性函数的特性，可以用来作经济预测，下面就以财政收入作为研究数据，预测2015年、2016年的值。

（1）网络的拓扑结构

由于影响财政收入的指标为X1、X4、X5三个，预测指标为财政收入一个，故选择输入节点为3，输出节点为1。节点的作用函数选取Sigmoid型函数，模型采用三层网络模型，其中隐层神经元12个，输出神经元4个。

（2）数据处理

将原序列数据分成两组，前组数据用来训练，后组数据用来检验。但是为了使网络权值都在[-1,1]之间，首先，必须把输入数据进行规一化处理，归一化公式为：其中xmax，xmin分别为原序列中的最大、最小值。

（3）网络训练

通过计算机编程不断的模拟，得出最佳的模型设置。选择自适应调整学习速率附加动量因子梯度下降反向传播算法训练函数，设置最大训练步数1000步，训练目标最小误差为0.001，学习速率0.05，训练效果显示：经过1000步的训练，网络的均方误差MSE=0.00833341小于0.01,达到了网络的训练要求。且网络的收敛速度是先下降,后又开始增加,之后一直速度平稳，这说明BP神经网络的中间层的神经数目选择非常合适。下面就采用该种设置的模型作为预测的网络模型,对此通过训练给出财政收入2008—2014的预测值，并与真实值进行比较，如表4所示，并对其作图（图2）进行比较。

表4 真实值与预测值比较

图2财政收入真实值与预测值对比

由表4发现，各年份真实值与拟合值之间的误差都比较小，可以说明模型精度较高，对此预测出2015年、2016年财政收入的值分别为32940164.15、37820068.38。

4 结论与建议

本文应用了小样本情景下预测效果优良的灰色预测模型来扩充样本容量，再采用BP神经网络给出各年份的拟合值，发现拟合效果较好，并对2015年、2016年的财政收入进行了预测。尽管上述模型对目标值的预测效果不错，也对每个影响指标的预测值进行了合理的检验，但是否符合今后财政收入的实际还有待于实践的检验。

[1]Liu S F,Forrest J.The Current Development Status on Grey System Theory[J].Journal of Grey System,2007,19(2).

[2]Guo B L,Guo L.A New APP Roaehto Visua lMotion Computation[J]. Joumal of Xidian University,1994,21(4).

[3]梅虎,朱金福,汪侠.基于灰色关联分析的旅游景区顾客满意度测评研究[J].旅游科学,2005,19(5).

[4]陈秀莲.泛珠三角国际旅游产业结构实证分析——基于次区域理论和灰色关联度的探讨[J].国际经贸探索,2007,23(7).

[5]洪涓,张楠.北京市旅游服务贸易发展影响因素灰色关联分析[J].经济论坛,2008,(8).

[6]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002.

（责任编辑/易永生）

F222；C812

A

1002-6487（2016）24-0082-03

国家自然科学基金资助项目(11201088)；安徽省高校优秀青年人才重点项目(gxyqZD2016300)；安徽省教育厅自然科学研究项目(KJHS2016B04)；黄山学院自然科学研究项目(2015xkj004；2015xkj005)

杨世娟（1988—），女，安徽安庆人，助教，研究方向：应用统计。

（通讯作者）卢维学（1989—），男，黑龙江依安人，助教，研究方向：数理统计。