成本函数的统计研究综述与应用

朱沛华，陈 林，2（.暨南大学 产业经济研究院；2.广州市自由贸易试验区研究基地，广州 50632）

成本函数的统计研究综述与应用

朱沛华1，陈 林1，2
（1.暨南大学 产业经济研究院；2.广州市自由贸易试验区研究基地，广州 510632）

近年来成本函数统计方法的兴起引起了学界的广泛关注。尽管成本函数理论的应用成果颇为丰硕，然而在国内并未出现一篇对其进行介绍推广及系统梳理的综述类论文。有鉴于此，在回顾成本函数理论的发展历史的基础上，详细分析了现今占据主流的各种成本函数形式的优点和缺陷。同时，基于大量国内外的优秀研究成果，文章依据成本函数理论实证应用最为广泛的生产领域——金融、公共事业和制造业展开论述，展望成本函数理论的未来应用方向和技术改进方法，以供相关研究者参考。

成本函数；超越对数成本函数；二次成本函数；复合成本函数；似不相关回归

0 引言

追溯成本函数的发展史，其统计研究始于20世纪80年代的国外，并在近十年来进入高峰期。较早的时候，即使理论上的成本函数形式多种多样，而实际上能够投入实证研究的只有C-D、CES等为数不多的成本函数形式。由于这两种函数在要素弹性及规模经济等方面的局限性，学术界开发了其他类型的成本函数。其中最具影响力的当属Christensen[1]等（1973）提出的超越对数成本函数（Translog Cost Function，简称TCF），这也是国内外的实证研究使用最多的回归模型。随后，Willing等(1982)[2]提出了二次成本函数（Quadratic Cost Function），Pulley和Braunstein (1992)[3]引入复合成本函数（Composite Cost Function），这些基于超越对数成本函数的变形亦受到了学界关注。

近年来，成本函数应用于各行各业的实证研究日趋丰硕，因此学界有必要对国内外数十年来的研究结果进行系统的整理。为此，本文在整理国内外相关研究文献的基础上，依据成本函数最为“青睐”的三种产业领域——金融、公共事业和制造业的研究成果进行理论综述，为今后的技术拓展提供理论上的铺垫。

1 成本函数统计的发展沿革与技术特征

1．1 C-D成本函数——经典形式的早期应用

在成本函数用于实证研究的起步阶段，部分学者引入C-D技术，设定C-D形式的成本函数，在研究金融行业方面有Benston（1972）[4]、Bell和 Murphy（1968）[5]等，也有

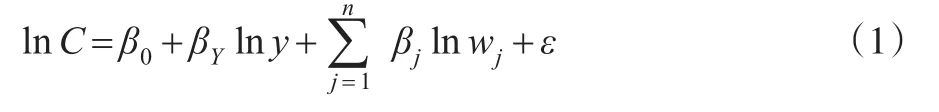
其中C为成本，y为产量，w为生产要素价格，β为待估参数，ε为随机误差项。方便起见，下文的所有公式的符号都根据这种规则来定。

然而，由于C-D成本函数本身的设定具有局限性，企业规模均具有不变的规模经济（不经济），导致在函数形式的设定上主观性较强，也不能拟合U型平均成本曲线。由于C-D成本函数受到诸多技术设定上的约束，使得该函数的应用范围有限。且尽管C-D成本函数可满足齐次性，替代弹性不变的假定，但是拓展到多种投入、多种产出的情况下，替代弹性不变的约束不能得到满足。

1．2 超越对数成本函数——研究方法的重大改进

鉴于C-D函数的局限性，国外的学者纷纷开始引进新的函数形式。Christensen等（1973）[1]提出超越对数成本函数（TCF），Fuss和McFadden（1978）[7]等在考虑了技术因素后进行拓展。该函数是通过对CES生产函数推导出的成本函数在一定特定点上进行泰勒级数展开而得到的。同时Christensen等（1973）[1]通过直接和间接检验，证明了基于超越对数的函数形式可以满足对称性和齐次性的约束条件。并且在特定情况下超越对数成本函数可退化为对数形式的C-D函数，即C-D函数是超越对数函数的特殊形式。与C-D成本函数相比，该函数中包含投入产出指标的À互影响项，对投入要素价格、产出采用对数平方的形式，从而使得该成本函数不受要素转换弹性不变和替代弹性不变的条件限制，因此可用于拟合多种产出与多种投入要素的生产情况，允许规模经济随着产出水平的变化而变化，经济含义明显。因此这种形式的成本函数受到了国内外学术界的广泛使用。其函数形式为：

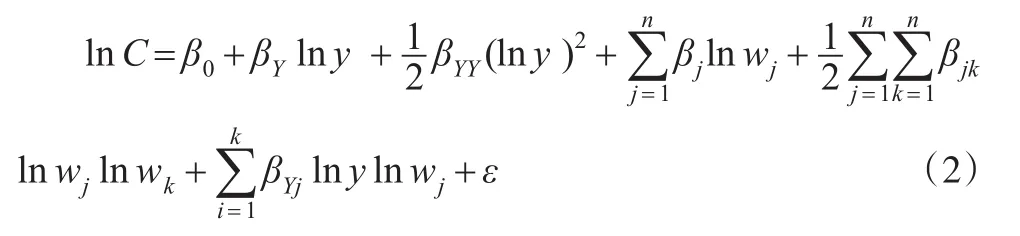
超越对数成本函数常用于估计规模经济与范围经济效应、要素替代弹性、测定自然垄断属性等，使用似不相关回归（SUR）估计方法对超越对数成本函数和相应的要素投入比例方程进行联合估计。国涓等（2010）[8]测度了中国工业部门的资本、劳动Morishima替代弹性。陈林和刘小玄（2015）[9]测定中国重化工业的规模经济效应等，该文使用1998—2008年中国重化工业的企业数据，以超越对数成本函数模型并结合似不相关回归法，测度了石油化工、农药、钢铁等6个重化工业的企业规模经济状况。

在实证研究中，超越成本对数函数方法在各个领域都得到了最为广泛的使用。然而该函数还是存在局限性。主要缺陷是该函数无法考虑产出为零的情况，已有的文献提供了两种解决办法，分别是使用一个接近于零的正值替代零产出与使用Box-Cox转换进行修正。前者会产生差别较大的估计范围经济的结果，进一步讲参数的估计决定接近零的确切范围和偏离的严重程度。因此可能产生较大的估计偏差。且取的正值具有主观性，没有可参考的客观标准。国外学者对这种方法尝试有Gilligan等（1984）[10]使用0.001代替0，Berger和Humphrey（1991）[11]用1代替0等。

后者是Christensen和Caves（1980）[12]提出来的修正超越对数成本函数的方案，通过Box-Cox因子对出现在函数中的独立产出的对数值替换得到广义超越对数成本函数（GTCF）。

Box-Cox因子替换如下：

当y=0时，有Yi=-1/θi。对式（2）的所有lny替换，假定多产出，可以得到广义超越对数成本函数：

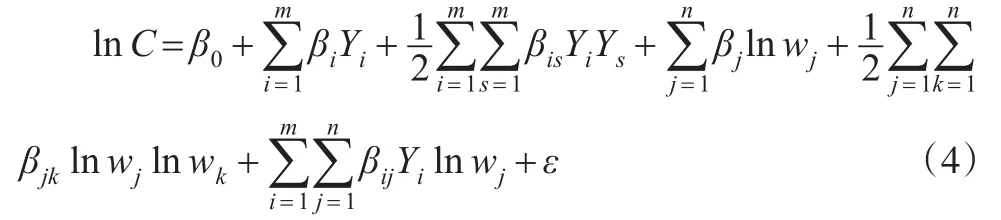
当θ→0时，则Y→lny。因此超越对数成本函数是广义超越对数成本函数的一种特殊情况。

广义超越对数形式的函数具备超越对数形式原有的特点，不仅能考虑联合生产，而且能考虑产出为零时的情况。该函数因为良好的性质也被运用于各行各业的实证研究中。

1．3 超越对数成本函数的进一步改良

与此同时，越来越多技术被引入成本函数的实证研究中，包括二次成本函数（QCF）、复合成本函数（CCF）等。

Baumol等（1982）[2]提出二次成本函数，是对成本函数的一般形式用多元函数泰勒公式在特定点处进行二阶导数展开。即：

二次成本函数的优点在于估计难度较低，可以直接用于测度规模经济和范围经济。然而也因为不存在线性齐次的假设条件、边际成本独立于要素价格而较受争议。

Pulley和Braunstein（1992）[3]在超越对数成本函数的基础上，把函数的产出结构的二次项和投入价格的对数二次项结合起来，首次提出复合成本函数的概念。其函数形式如下：

该函数的产出采用二次结构，考虑特定产出为零的情况，更加适用于测度规模经济、范围经济与成本次可加性。函数形式没有要求投入与产出之间可分，也没有约束投入比例和成本份额必须独立于产出水平，且投入价格的对数二次项有利于线性齐次的先验条件成立。另一方面，它对每种产出的投入需求弹性等于或独立于投入价格没有限制。且函数形式可变，具备足够自由的参数用于二阶微分估计。该函数和超越对数成本函数形式较为相似，拥有相同的参数，并要求函数形式对称和线性齐次。

在国外学者的研究中，还存在多种成本函数，诸如广义里昂惕夫成本函数、广义C-D成本函数等。鉴于以上函数的应用研究相对偏少，且国内学者采纳应用的研究成果较少，在此不一一介绍。

2 金融领域中成本函数的应用

2．1 保险业

保险业内，Cummins和Weiss（1993）[13]构建超越对数成本函数，对1980—1988年样本内三种不同规模的财产保险公司的规模经济效应进行探讨，发现中型和小型的财险公司的规模经济最为显著。Rai（1996）[14]以1988—1992年11个发达国家主要的保险公司数据为样本，分别使用SFA法和自由分布法对成本函数进行回归分析，对比研究了它们的成本效率和X效率的差异。

在国内，黄薇（2006）[15]使用SFA方法结合超越对数成本函数测度了1999—2004年中国28家寿险和非寿险保险公司的成本效率，发现多元化产品的经营模式利于提高保险公司的成本效率。刘志迎等（2007）[16]在对数C-D成本函数的基础上采用SFA方法分析了1999—2004年我国16家财产保险公司的成本效率，就影响我国财险业成本效率的主要因素进行详细的分析，且发现外资财险公司的成本效率整体高于中资财险公司。叶成徽和陈晓安（2012）[17]基于C-D成本函数的SFA法构建随机前沿成本效率和随机前沿利润效率模型，中国人寿、中国平安和中国太保三家上市保险公司为研究对象，分析经理薪酬对保险公司效率的影响程度。

2．2 银行业

另一方面，银行业在金融领域占有重要的地位，成本函数应用于银行业的实证结果更是汗牛充栋。在早期的研究中，Benston（1972）[4]、Bell和Murphy（1968）[5]使用对数线性C-D成本函数对银行业的规模经济效应进行研究，系统地分析了每一项银行服务产品的直接和间接经营成本，并发现其他条件不变时，如果银行规模扩大一倍，将引起企业平均成本下降5%～8%。刘宗华和邹新月（2004）[18]指出，Benston（1972）[4]、Bell和Murphy（1968）[5]的样本中主要是小型银行，从小银行的规模经济效应而推出包括大型银行在内的所有银行都具有规模经济在逻辑上行不通，且未能将分支机构的规模经济和整个银行的规模经济区分开来。在国内钱蓁（2003）[19]使用对数C-D成本函数，结合SFA方法对影响国内银行X-低效率的因素进行了具体分析，结果表明自有资本比例、所有权结构安排、利息收入占总营业收入的比重是三个重要的影响因素。

20世纪80年代后的海外研究通过采用其他形式的成本函数对早期的关于银行业的实证分析进行了改进。Mester（1987）[20]以美国加州地区内商业银行1982年的数据为样本，设定商业银行的产出为抵押贷款、其他贷款和其他流动性投资，构建多产出的超越对数成本函数模型来研究样本银行的次可加性，并采用联合假设检验来提高模型的说服力，指出加州的商业银行并不具有自然垄断属性。同时Mester也指出，Bell和Murphy（1968）[5]等分析银行业具有显著的规模经济特征是由于使用单产品或者使用一种产品代替其他产品进行建模，忽略了范围经济效应。Hunter等（1990）[21]分别使用超越对数成本函数和依据成本函数构建多产出模型分析美国1986年311家规模最大的商业银行的成本特征，并使用网格搜索法对Evans和Heckman（1984）[22]提出成本次可加性检验进行拓展，最后两个模型都表明美国大型商业银行在多产出模型分析下不具有成本次可加性，从而该产业不是自然垄断产业。

纵观国内商业银行市场，在政府地产业扶持政策和严格限制市场准入的背景下，商业银行发展势头更为迅猛，资产规模也远高于国外其他银行，更加受到国内学者的重视。杜莉和王锋（2002）[23]以银行业资产专用性的理论视角，结合广义超越对数成本函数模型考察1995—1999年国内商业银行的成本运营状况，从理论和实证上证明了扩大经营范围对银行范围经济效应的正向影响。刘宗华和邹新月（2004）[18]以1994—2001年我国国有银行及股份制银行为样本，采用对偶法把银行的产出分为存款、投资和未还清贷款，使用广义超越对数成本函数进行估计，结果显示我国商业银行存在着规模经济效应，国有银行的规模经济显著而股份制银行存在轻微的规模不经济。迟国泰等（2005）[24]对样本数据分别做相应的趋同处理，解决了因银行数据离散度大而导致估计结果失真的问题，基于SFA方法，利用超越对数成本函数模型评估了中国14家主要商业银行在1998—2003年的成本效率情况，结果表明，在忽略贷款产出质量的情况下，国有商业银行成本效率要高于股份制商业银行，而考虑贷款产出质量时，国有商业银行的整体成本效率要落后于股份制商业银行。成刚（2006）[25]使用复合成本函数拟合国内商业银行1998—2003年的数据，在模型中引入截面单位和时间虚拟变量，发现横截面单位对模型的影响显著，而银行的规模经济和范围经济受时间的影响不显著。刘孟飞和张晓岚（2013）[26]构建基于SFA方法的超越对数成本函数模型，将资产回报率三因子模型计算出的系统性风险值代入SFA方法中的无效率效应模型，对2007—2011年国内16家上市银行的成本效率进行评估，发现不考虑风险因素会导致无效率值的明显高估，而适当降低风险有利于银行成本效率的提高。

综上所述，成本函数在金融行业不仅应用广泛，而且使用形式不限。尽管大多数研究是基于超越对数成本函数和广义超越对数成本函数来研究，但是当这两种模型出现不足时，可以选用其他类型的函数来弥补，同时需要对每种成本函数的优劣之处有清晰的认识。在实际运用中需要对总成本的计算有清晰的界定。成刚（2006）[25]指出，成本函数中的总成本项必须是各项投入指标之和，不应包括投入指标之外的其他成本，否则无法满足成本函数计算的限制条件。国内对商业银行的研究文献忽略了这个问题，可能导致规模经济评价结果的偏误，这需要引起相关研究的注意。

3 公共事业领域中成本函数的应用

3．1 市政公用行业

电力行业方面，从Nerlove（1963）[6]采用C-D成本函数对美国供电行业的规模收益进行分析以来，许多学者相继开始对电力行业进行实证研究。Christensen和Greene（1976）[27]引入超越对数成本函数，以美国1955年与1970年电力企业的截面数据为样本进行分析。Kaserman和Mayo（1991）[28]首次采用多产出范围经济的概念来分析纵向合并的成本效率优势。通过构建二次成本函数模型，对1981年美国74家企业的横截面数据进行估计，为企业的纵向合并提供有力的理论依据。Fraquelli等（2004）[29]以25家意大利当地电力公用企业1994—2000年的数据为样本，通过构建一个多产出的复合成本函数，进行加总规模报酬估计，考察电力产业纵向合并战略所带来的成本效率的提高程度。在国内，任宇宁和赵国庆（2007）[30]通过构建非齐次C-D生产函数，在产出成本最小化的条件约束下得到相应的具有面板数据形式的成本函数模型。以2003年一季度到2004年四季度中国大陆地区供电行业数据分析资本和劳动力要素投入对企业规模收益及经营效率的影响程度。

鉴于数据的可得性，国内运用成本函数对供水、燃气供应行业的研究并不多见，而国外的研究更为丰富。Hayes（1987）[31]将产出归类为零售供水以及批发供水，构建二次成本函数多产出模型考察美国475个供水公共事业公司的规模经济和范围经济效应，发现美国大型供水公司存在范围不经济，鼓励零售供水和批发供水共存的经营模式有利于降低企业的成本。Kim（1987）[32]给予多产出的超越对数成本函数模型，根据不同的经济特征将供水业的产出分为居民用水、商业用水和工业用水，对美国供水业居民用水和非居民用水的规模经济效应进行研究，并发现供水业整体上规模经济不变。Gordon等（2003）[33]运用超越对数成本函数和嵌套C-D成本函数分析了加拿大天然气运输业，发现其符合鲍莫尔等人提出成本次可加性，从而判定加拿大天然气运输业具有自然垄断属性。

3．2 交通运输行业

成本函数用于研究À通运输业主要在于铁路、航空运输业，一方面在于数据较容易取得，行业集中度高，另一方面其他运输业诸如公路、水运等数据零散且不易准确取得。由于这两种运输行业有最为明显的规模经济特征，运用成本函数研究更具有经济意义。Hansen等（2001）[34]以10家美国本土的航空公司的季度数据为样本，结合超越对数成本函数探讨最为显著影响该行业成本的基本因素。Chua等（2005）[35]则研究的是航空联盟对航空公司成本的影响效应，他们发现，航空联合不利于大型成员公司成本的降低，反而利于小型成员公司提高成本效率。

铁路行业方面，Sanchez（2000）[36]运用超越对数成本函数研究1973—1990年欧洲铁路业的成本状况，进行成本次可加性检验，发现欧洲铁路业并不具有自然垄断属性。Bitzan和Keeler（2003）[37]将时间变量引入超越对数成本函数，考虑1983—1997年美国铁路货物运输的增长趋势，实证表明1983年以来铁路业的技术进步大幅度地削减了该行业的运输成本。陈维亚等（2008）[38]利用超越对数成本函数考察中国部分第三方物流业1999—2007年的规模经济和技术进步效应，结果显示，以11家企业为样本的第三方物流从总体上存在轻微的规模不经济。

3．3 电信行业

在公用事业中，电信行业也被认为是规模经济特征十分明显的行业之一。Evans和Heckman（1984）[22]研究美国电信行业的成本函数时，在Baumol等人提出的成本次可加性的理论基础上开创了新的对自然垄断属性的检验方法，只要当单个企业生产相同产量的成本低于两个或以上的企业加总生产的加总成本，即可认为具有成本次可加性。运用这种检验发现，1958—1977年间美国电信业集中度过高，企业规模超过平均成本曲线的最低点，处于经营不效率的状态。

Bloch等（2001）[39]使用复合成本函数估计澳大利亚电信行业的成本特征，研究表明，1926—1991年间该行业表现出范围经济，但是不具有成本次可加性。Sung和Gort（2000）[40]基于超越对数成本函数研究美国电信行业，实证结果表明放宽电信产业的市场准入壁垒、增加竞争对成本效率的提高起促进作用，对美国大型电信公司的纵向合并带来的成本节约效应提出了质疑。

公用事业由于其明显的规模经济特征而常常被直接定性为自然垄断产业，政府往往严格规制新企业的进入。然而这同时会造成市场一家或者几家独大从而缺乏竞争，造成生产效率低下的问题。但实际上这些产业是否具有自然垄断属性则需要定量分析来确定。如果研究证明该产业并非自然垄断产业，引入竞争则是有利于增进社会福利。同时，由于公用企业规模普遍较大，内部管理的À易成本也相应偏高，同时企业容易处于并非最优经营的状态，尤其是要素投入的配比状态。通过研究要素投入的替代弹性，调整要素投入比例，有利于企业运营成本的降低。

4 制造业领域中成本函数的应用

4．1 重化工业

重化工业的自然垄断测度在国外较为常见，本文在此不赘述。但在国内，受制于要素价格数据的缺乏和资本价格估算法的落后，国内学术界鲜有定量测度行业自然垄断属性的研究。为此，陈林和刘小玄（2014）[41]基于现代自然垄断理论的框架，以超越对数成本函数模型估计了中国重化工业的成本函数形式，进而对其自然垄断属性进行了测度。

值得一提的是，自然垄断是一个产业层面的学术概念——只有某某行业是自然垄断，而不能说某某企业是自然垄断。规模经济则基本上是一个企业层面的学术概念——只有某某企业是规模（不）经济，而不能说某个行业在一个总产量上是规模（不）经济。因此，超越对数成本函数既可以研究产业的业态特征，也可以研究企业异质性，是一种多用途的、稳健的基础计量模型。

4．2 能源行业

鲁成军和周瑞明（2008）[42]基于超越对数成本函数与不变替代弹性约束条件，结合技术进步和产出效应计算Morishima替代弹性（MES），对中国工业部门能源、资本和劳动之间的绝对替代弹性和相对替代弹性进行了测算，研究表明能源与劳动呈现替代关系，能源与资本的替代关系并不显著。黄光晓和林伯强（2011）[43]基于元分析法量化分析中国工业部门关于资本和能源替代的研究成果，以8个样本文献对超越对数成本函数进行元回归，计算Morishima替代弹性（MES）和À叉替代弹性，研究表明模型假设的差异是造成结果异质的主要因素，文章重新测算了资本能源替代弹性，发现长期中两者存在稳定的替代关系。樊茂清等（2012）[44]采用超越对数成本函数建立包括33个部门的联立方程计量模型，以相应的1981—2005年的数据为样本，分别从静态和动态视角研究了能源价格变化、技术变化和ICT投资等因素变化对中国33个部门能源强度的影响机制。

Bentzen（2004）[45]基于超越对数成本函数研究1949—1999年间的美国制造业，使用动态OLS、SUR估计得出相应的成本份额方程结果，将反弹效应与要素价格弹性和替代弹性联系起来，计算出能源需求的反弹效应大约是24%。国涓等（2010）[8]在超越对数成本函数的基础上，施加能源价格非对称影响约束，使用Morishima替代弹性（MES）模型测算国内工业部门能源需求的反弹效应为39.48%，高于发达国家的水平。

由于制造业庞大的经营体系，学术界对其的研究方法也层出不穷。成本函数可用于测算重化工业规模经济、范围经济与成本次可加性（即自然垄断属性），也可以通过测算行业的TFP值来研究企业的技术进步与成本效率，更是可以通过研究生产要素之间的替代弹性来分析企业内在生产关系。从多方面研究的展开有利于企业自身对产业整体经济效益的认识，优化企业层次和产业组织层次经营模式；也有利于对症下药，给予政府足够的理论依据进行配套的产业规制。

5 简要评述

综合以往众多学者的研究成果，可见成本函数在企业规模较大的产业颇有建树。但同时本文也认识到成本函数作为研究工具还存在着不足。

首先，不同形式的成本函数都存在着局限性，研究在选用模型时务必对应成本函数模型的应用条件。与此同时，成本函数在不考虑全要素生产率因素的前提下，可能会造成相关系数的虚高，造成估计结果的偏误，回归成本函数时需要注意拟合效果的准确性。这是今后学界值得拓展的研究领域。

其次，纵观国内的主要研究方法，主要集中于C-D、超越对数、广义超越对数成本函数。而二次、复合成本函数的相关研究则显得凤毛麟角。同时，国外学者也有运用广义里昂惕夫成本函数、广义C-D成本函数成本函数进行实证研究，但是这些函数尚未被国内学者所采用。这也是未来国内成本函数研究的一个发展方向，成本函数的研究呈现形式多样化的趋势。

最后，成本函数的适用性有待提高。本文搜集了大量的研究文献，发现国内成本函数的研究领域较之国外研究成果显得更为狭窄，譬如国外在航空运输、铁路运输、电信、供水等公用事业以及大型制造业的成本函数相关研究成果汗牛充栋，而国内相关研究则相对空白。部分原因在于，相关行业财务数据的不透明性导致样本数据采集无法展开。其中资本价格的确定需要相当多的企业财务数据，而这又是成本函数回归成败的关键，因此数据上的制约在成本函数统计研究中尤为明显。但随着现代企业财务公开制度的不断健全，相信这些行业的成本函数研究也会丰富起来。相关研究有待学界共勉。

[1]Christensen L R,Jorgenson D W,Lau L J.Transcendental Logarith⁃mic Production Frontiers[J].Review of Economics and Statistics, 1973,55(1).

[2]Willig R,William J,Panzar J C.Contestable Markets and the Theory of Industry Structure[M].New York:Harcourt Brace Jovanovich,1982.

[3]Pulley L B，Braunstein Y M.A Composite Cost Function for Multi⁃product Firms With an Application to Economies of Scope in Banking [J].Review of Economies and Statistics，1992，74(5).

[4]Benston G J.Economics of Scale of Financial Institutions[J].Journal of Money,Credit and Banking，1972,(4).

[5]Bell F W，Murphy N B.Costs in Commercial Banking:A Quantita⁃tive Analysis of Bank Behavior and It's Relation to Bank Regulation [J].Journal of Finance,1969,24(1).

[6]Nerlove M.Returns to Scale in Electricity Supply[M].Stanford:Stan⁃ford[M].University Press,1963.

[7]Fuss M,McFadden D.Production Economics:A Dual Approach To Theory and Application[M].Amsterdam:North-Holland，1978.

[8]国涓,郭崇慧,凌煜.中国工业部门能源反弹效应研究[J].数量经济技术经济研究，2010，(11).

[9]陈林,刘小玄.产业规制中的规模经济测度[J].统计研究，2015,32 (1).

[10]Gilligan T，Smirlock M，Marshall W.Scale and Scope Economies in the Multi-product Banking Firm[J].Journal of Monetary Economics，1984,13(3).

[11]Berger A N,Humphrey D B.The Dominance of Inefficiencies Over Scale and Product Mix Economies in Banking[J].Journal of Mone⁃tary Economics,1991,28(1).

[12]Caves D W，Christensen L R,Tretheway M W.Flexible Cost Func⁃tions for Multiproduct Firms[J].The Review of Economics and Statis⁃tics，1980,62(3).

[13]Cummins J D，Weiss M A.Measuring Cost Efficiency in the Proper⁃ty-liability Insurance Industry[J].Journal of Banking&Finance，1993,17(2－3).

[14]Rai A.Cost Efficiency of International Insurance Firms[J].Journal of Financial Services Research，1996，10(3).

[15]黄薇.基于SFA方法对中国保险机构效率的实证研究[J].南开经济研究，2006,(5).

[16]刘志迎,孙文平,李静.中国财产保险业成本效率及影响因素的实证研究[J].金融研究，2007,(4).

[17]叶成徽,陈晓安.经理报酬对中国上市保险公司效率的影响——基于随机前沿（SFA）方法的实证研究[J].保险研究，2012,(8).

[18]刘宗华，邹新月.中国银行业的规模经济和范围经济一基于广义超越对数成本函数的检验[J].数量经济技术经济研究，2004,(l0).

[19]钱蓁.中国商业银行的效率研究——SFA方法分析[J].南京社会科学,2003，(1).

[20]Mester L J.A Multiproduct Cost Study of Savings and Loans[J].The Journal of Finance，1987,42(2).

[21]Hunter W C,Timme S G,Yang W K.An Examination of Cost Subad⁃ditivity and Multiproduct Production in Large U.S.Banks[J].Journal of Money,Credit,and Banking 1990,22(4).

[22]Evans D S,Heckman J J.A Test for Subadditivity of the Cost Func⁃tion With an Application to the Bell System[J].The American Eco⁃nomic Review，1984,74(4).

[23]杜丽，王锋.中国商业银行范围经济状态实证研究[J].金融研究，2002，268(10).

[24]迟国泰,孙秀峰,芦丹.中国商业银行成本效率实证研究[J].经济研究，2005，(6).

[25]成刚.中国银行业规模经济和范围经济的实证研究——基于复合成本函数的分析[J].中央财经大学学报，2006，(7).

[26]刘孟飞,张晓岚.风险约束下的中国上市银行效率问题研究[J].数量经济技术经济研究，2013，(2)．

[27]Christensen L,Greene W.Economies of Scale in US Electric Power Generation[J].Journal of Political Economy，1976,84(4).

[28]Kaserman D L,Mayo J W.The Measurement of Vertical Economies and the Efficient Structure of the Electric Utility Industry[J].Journal of Industrial Economics，1991,39(5).

[29]Fraquelli G,Piacenza M，Vannoni D.Cost Savings From Generation and Distribution With an Application to Italian Electric Utilities[J]. Journal of Regulatory Economics，2005，28(3).

[30]任宇宁,赵国庆.基于面板数据的中国供电行业规模收益分析[J].统计研究，2007，(4).

[31]Hayes K.Cost Structure of the Water Utility Industry[J].Applied Economics，1987，(19).

[32]Kim H Y.Economies of Scale in Multi-product Firms:An Empirical Analysis[J].Economica，1987,54(214).

[33]Gordon D V,Gunsch K,Pawluk C V.A Natural Monopoly in Natural Gas Transmission[J].Energy Economics,2003,25(5).

[34]Hansen M M,Gillen D,Djafarian-Tehrani R.Aviation Infrastructure Performance and Airline Cost:A Statistical Cost Estimation Ap⁃proach[J].Transportation Research Part E:Logistics and Transporta⁃tion Review,2001,37(1).

[35]Chua C L，Kew H，Yong J.Airline Code-share Alliances and Costs Imposing Concavity on Translog Cost Function Estimation[J].Re⁃ view of Industrial Organization，2005,26(4).

[36]Sânchez P C.A Subadditivity Test for the Cost Function of the Prin⁃cipal European Railways[J].Transport Reviews，2000，20(3).

[37]Bitzan J D，Keeler T E.Productivity Growth and Some of Its Deter⁃minants in the Deregulated U.S.Railroad Industry[J].Southern Eco⁃nomic Journal,2003,70(2).

[38]陈维亚,陈治亚,周伟丽.第三方物流企业规模经济的实证研究[J].商业经济与管理，2008,206(12).

[39]Bloch H,Madden G,Savage S J.Economies of Scale and Scope in Australian Telecommunication[J].Review of Industrial Organiza⁃tion,2001,18(2)

[40]Sung N,Gort M.Economies of Scale and Natural Monopoly in the U. S.Local Telephone Industry[J].The Review of Economics and Statis⁃tics，2000,82(4).

[41]陈林,刘小玄.自然垄断的测度模型及其应用——以中国重化工业为例[J].中国工业经济，2014,(8).

[42]鲁成军,周瑞明.中国工业部门的能源替代研究——基于对AL⁃LEN替代弹性模型的修正[J].数量经济技术经济研究，2008，(5).

[43]黄光晓,林伯强.中国工业部门资本能源替代问题研究--基于元分析的视角[J].金融研究，2011,372(6).

[44]樊茂清,郑海涛,孙琳琳,任若恩.能源价格、技术变化和信息化投资对部门能源强度的影响[J].世界经济，2012,(5).

[45]Bentzen J.Estimating the Rebound Effect in US Manufacturing Ener⁃gy Consumption[J].Energy Economics,2004,26(1).

（责任编辑/易永生）

O212.1

A

1002-6487（2016）24-0023-05Nerlove（1963）[6]等研究电力行业的规模收益状况。

国家自然科学基金资助项目（71203078；71333007）；广东省软科学研究计划项目（2014A070703019）；广东产业发展与粤港澳台区域合作研究中心资助项目（52702497）

朱沛华（1992—），男，广东东莞人，硕士研究生，研究方向：产业经济。

陈 林（1981—），男，广东河源人，副教授，博士生导师，研究方向：产业经济。