基于随机抽取的AR模型定阶和参数评估

刘 源，尹慧萍，朱建平,2(.太原理工大学 数学学院，太原 030024；2.厦门大学 管理学院,福建 厦门 36005)

基于随机抽取的AR模型定阶和参数评估

刘 源1，尹慧萍1，朱建平1,2
(1.太原理工大学 数学学院，太原 030024；2.厦门大学 管理学院,福建 厦门 361005)

文章基于对平稳时间序列数据的随机抽取，选用AR模型研究其模型定阶方法和参数评估准则。根据数据有序性的特点，提出利用交叉验证的方法确定自回归模型阶数，并通过对原数据的无放回抽取实现对系数参数估计的评估。实例分析结果表明，交叉验证的定阶与AIC准则定阶结果保持较高一致性，新的参数评估在一定的模型误差范围内可以得到更为简单有效的系数估计区间。

随机抽取；AR模型；模型定阶；参数评估

0 引言

时间序列分析的时域方法研究一般是分析样本的自相关函数，并建立参数模型来描述序列的动态依赖关系。常用的模型有自回归模型（Auto-regressive，AR）、移动平均模型（Moving Average，MA）和混合模型（Auto-regressive Moving Average，ARMA）。由Wold分解定理[1]可知，任何一个具有有限方差的ARMA过程和MA过程都可以表示成AR过程，而且对AR模型参数估计得到的是线性方程，计算简便，所以基于AR模型的研究是最常见的。

在AR的建模过程中，对于阶数的确定和模型参数的估计是建模中很重要的步骤。从自相关函数出发的模型定阶与参数估计一直是时间序列分析的主要研究方向之一。在时域中多数学者采用构造统计量的方法来确定模型的阶数，确定有效阶数后对AR模型的参数进行求解估计。在频域中，平稳时间序列的自相关函数是功率谱密度函数，人们根据计算时间和精确度提出适用不同应用场合的多种算法，例如L-D递推算法、Gram-Schmidt正À法等[2]。信息准则法在时间序列模型选择中也起着很重要的作用，AIC准则是Akaika(1973)基于对数化的似然函数设计的一个方法来近似K-L距离，该准则既考虑拟合模型对数据的接近程度，也考虑模型中所含待定参数的个数。与使用R2作为标准一样，AIC有着良好的理论依据[3]，Akaika在1976年改进的BIC方法避免了大样本情况下AIC准则在选择阶数时收敛性不好的缺点。

本文主要从时域方法角度对时间序列进行探讨，对于模型阶数的确定，借鉴PCR、PLS回归建模中常用的À叉验证方法，通过double-foldÀ叉验证，用两次所得的均方预测误差和来确定模型阶数的选取。在模型参数估计的评估中，使用随机多次抽取原时间序列部分数据进行参数估计，从预测精度和模型稳健性两方面来评价自回归方程。

1 AR模型及其计算方法

一般来说，以时间序列数据为依据的实证研究分析都必须假定有关的时间序列是平稳的，否则会导致谬误回归的出现。本文中模型阶数确定和参数估计中进行随机抽取也需要所研究序列的平稳性这一假设，这样使得自回归模型的假设条件满足经典线性回归模型。所以首先对原始序列进行检验判别平稳性，若序列不平稳则通过差分使数据达到平稳。

1．1 AR模型简介

设平稳时间序列{yt}是一个AR(p)过程，则序列{yt}满足：

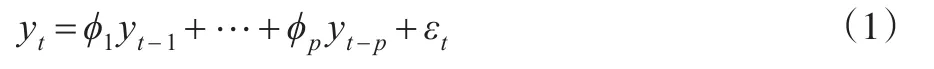
其中，{εt}是随机误差序列，对于任意的t，满足假设条件E(εt)=0，Var(εt)=σ2＞0，Cov(εi，εj)=0，i≠j。ϕ1，…，ϕp称为自回归系数。

记Bk为k步滞后算子，则AR(p)平稳的条件是滞后算子多项式ϕ(B)=1-ϕ1B-…-ϕpBp的根均在单位圆外。对AR(p)进行参数估计常用的方法是最小二乘估计和极大似然估计，本文采用极大似然法估计参数，并计算中不同阶数下的AIC值变化。

1．2 阶数确定

PCR、PLS回归建模中的À叉验证是为了选取多个主成分来做回归分析，校验每个主成分下的PRESS值，选择PRESS值小的主成分数，这样可以得到可靠稳定的模型[3]。

利用double-foldÀ叉验证来确定模型的阶数p，将原始数据集{yt}均分为两份样本：一份样本被保留作为测试集，另一样本用来做训练，用测试集去验证；之后再将训练集作为测试集，测试集作为训练集进行迭代一次，将两次所得的误差和作为预测误差[4]。

本文定义：

其中，V表示均匀分割的两个不相À数据集，记作ν1、ν2，ϕˆ(-ν)是基于ν数据集的数据进行的参数估计，Q(ν)是在ν数据集上定义的函数，用均方预测误差来衡量拟合的优劣，其定义为：

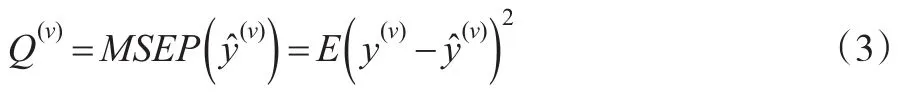
使得CVscore最小的p为最佳模型阶数[5，6]。

当原序列数据的个数n很大的情况下，可以随机抽取部分数据做À叉验证，具体操作是：从原始数据集{yt}中随机抽取一段数据作为测试集，再从中抽取与测试集不相À的一段数据作为训练集，之后进行double-foldÀ叉验证计算CVscore值。在平稳时间序列的假设条件下，随机抽取部分数据作为研究集可以避免数据量庞大带来的复杂计算过程。

在评价回归方程的标准当中，残差平方和RSS从数据与模型拟合优劣的角度出发，反映了实际数据与理论模型的偏离程度；也可以从预测精度出发导出选取自回归的变量集，看预报值与真实值偏离程度，而CVscore的计算兼有两者，使得模型在阶数的选取上更为稳定可靠。

1．3 评估

对于时间序列数据的建模分析，大多关注于两个方面：一是预测性能，是否确定阶数后的自回归变量和其对应的回归方程可以对没有参与模型参数估计的数据进行合理的预测；二是回归自变量的稳定性，时间序列相邻的数据之间的依赖关系是有变化的，不同数据集下模型的自变量系数参数估计是会略有不同的。另外，评价模型需要基于独立的数据集。

本文提出基于随机抽取的模型预测评估，如下所示：

（1）在原始序列数据中随机选取n1长度的数据集作为训练集，剩余的数据集n2作为测试集，其中n1+n2=n。本文使用

（2）利用训练集中的时间序列数据进行AR模型的参数估计，本文使用double-foldÀ叉验证确定的阶数p。

（3）用训练集得出的回归方程预测测试集中的数据，计算均方预测误差MSEP。

（4）为了避免选取数据集时的偶然性，重复步骤（1）至步骤（3）300次，每一次都有新的随机抽取训练集和MSEP的计算。

对于以上的预测评估方法，可以评估出自回归当中稳定的自变量参数估计的范围。其基本原理是，如果自回归中的自变量是重要的或者稳定的，那么它的估计系数就会为不同数据集建立的模型变量而多次出现在一定的数值范围内。由于时间序列数据的有序性以及无法获得多个独立的数据集，采取了随机抽取的办法。在一定的误差范围内，记录自回归模型中某一自变量系数参数多次估计得到的数值，得到稳定的合理估值范围。

AR模型作为回归模型，系数参数的估计是可以通过Bootstrap的模拟重抽样来估计系数的分布[7]。本文把原始数据集{yt}当做总体，从中有放回的重新抽样，重抽样样本大小仍为n，可以构造得到系数参数估计的置信区间。本文通过预测评估方法得到系数参数的估计区间是在对序列{yt}无放回的部分数据随机抽样并进行参数估计，在大致确定的模型预测误差范围内得到简单有效的多次系数估计分布图。

2 实例分析

本文选用小木虫网站上公开的数据集：氧的同位素水平，该数据是在3000年时间里反向时间的180对160的同位素比率，相邻数据之间的时间间隔为3年，这对于研究气候模式和气候变化，以及地球轨道的动力学研究有很大的参考价值。

本文把原始数据转变成正向时间序列数据后，对其进行平稳性检验，通过调用R软件包fUnitRoots中的urdfTest (x)函数，分析结果为F统计量5.171，p值为0.005854，则拒绝原假设，认为同位素比率序列数据是平稳的[8]。

利用前文中提到的double-foldÀ叉验证来确定模型的阶数，计算p取不同值时的CVscore值，找到使之最小的p为最佳模型阶数；并且通过与不同阶数下的AIC值进行对比，考察定阶方法的有效性(对CVscore值和MSEP值进行同倍放大减去同数的处理，使其和AIC值随阶数的变化可以在同一个图中观察)。

图1 CVscore和AIC定阶曲线图

从图1中可以看出，AIC的曲线在阶数p到达3以后变化呈现出稳定的态势，在12处取得最小值，得到最优自回归变量集（AIC值为R软件中arima0(x)函数计算所得）；CVscore曲线和两个训练集下的MSEP曲线都是随着 p的增大而逐渐上升，CVscore值分别在3、5和12处最小或变化最小，与AIC准则的判别结果保持一致。这表明利用À叉验证确定最优集的阶数是可行的。

根据本文所提出的基于随机抽取的模型预测评估操作实现，得到了在阶数p为3时，300次随机抽取的训练数据的参数估计及其预测方差。

图2 300次估计参数和预测误差分布图

图2分别为一次随机300次自回归变量的第一至第三的系数估计与预测误差的直方图和密度估计曲线，MSEP值的分布显示，300次随机抽取模型估计的预测误差90%以上是在数值16～18的范围内的，模型的多次估计是稳定有效的。在参数的估计方面，ϕ1系数估计有30%以上在(1.05，0.1)中，ϕ2的估计值有将近一半在(- 0.15，-0.1)的范围，ϕ3的估计40%以上落在了(- 0.14，-0.12)内；分布范围中，ϕ2的取值范围远大于其他系数范围，表明自回归变量yt-2在自回归模型建模中并没有yt-1和yt-3稳定。

表1 系数参数的Bootstrap

本文做出模拟500次的自回归模型的Bootstrap，得到回归系数参数估计的95%的置信区间。通过对比可以发现，表1中得到的yt-1、yt-2和yt-3系数的置信区间与图2中随机抽取得到的各个系数估计分布图的数值上下限相一致；自回归变量yt-2系数估计显著性检验（p值＞0.05）表明该变量在模型中的不稳定性，参数置信区间的估计范围也相对较大。另外，新提出的参数评估方法可以更为方便准确地找到模型系数参数稳定的估计区间，同时也避免了由回归变量不稳定引起的系数参数估计未通过显著性检验而没有统计学意义的问题。

3 总结

本文以AR模型为研究模型，针对平稳的时间序列数据，提出了基于随机抽取的模型定阶方法和参数评估。通过氧同位素比率的数据进行实例分析，结果表明double-foldÀ叉验证来确定模型的阶数是可行有效的，以原始数据为样本的随机抽取可以得到一定模型误差范围内稳定合理的系数估计区间。

由于时间序列数据有序性的特征，À叉验证并不是真正的；在序列长度n很大的情况下，随机抽取部分数据进行À叉验证更为简便可行。本文提出的参数评估，较之回归模型Bootstrap的参数估计置信区间，估计区间更为简单有效，并且避免了数据量很大时统计检验失效的情况。

[1]Kay S M,Marple S L.Spectrum Analysis——A Modern Perspective [J].Proceedings of IEEE,1981,69(11).

[2]衡思坤,郭昊坤,吴军基,应展烽.离散序列AR模型定阶方法研究[J].微计算机信息,2012,28(9).

[3]Xu Q S,Liang Y Z.Monte Carlo Cross Validation[J].Chemometrics and Intelligent Laboratory Systems,2001,(56).

[4]Burnham K P,Anderson D R.Model Selection and Multimodel Infer⁃ence:A Practical Information-Theoretic Approach[M].New York: Springer,2002.

[5]Huang J,Ma S G.Variable Selection in the Accelerated Failure Time Model via the Bridge Method[J].Lifetime Data Anal,2010,16(2).

[6]Jiang P,Wu H N.RF-DYMHC:Detecting the Yeast Meiotic Recom⁃bination Hotspots and Coldspots by Random Forest Model Using Gapped Dinucleotide Composition Features[J].Nucleic Acids Re⁃search,2007,(35).

[7]Kohavi R.A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection[J].Computer Science Department, 1995.

[8]薛毅,陈立萍.R统计建模与R软件[M].北京：清华大学出版社，2007.

（责任编辑/易永生）

O211.61

A

1002-6487（2016）24-0016-03

刘 源（1991—），男，山西五台人，硕士研究生，研究方向：数据挖掘。

尹慧萍（1990—），女，山西太原人，硕士研究生，研究方向：数据挖掘。

（通讯作者）朱建平（1962—），男，山西太原人，教授，博士生导师，研究方向：数理统计、计量经济。