基于重要点与灰色GM（1,1）模型的时间序列分段算法

江艺羡，张岐山（福州大学 经济与管理学院，福州 350108）

基于重要点与灰色GM（1,1）模型的时间序列分段算法

江艺羡，张岐山
（福州大学 经济与管理学院，福州 350108）

重要点分段法主要利用局部极值点进行划分，可以将时间序列分割成若干个相对较短但不重叠的子序列。该方法在进行序列划分时，能够既保留全局特征，又保持局部性质，是时间序列分段常用的方法之一。文章采用重要点分割法将序列分割成子序列，之后采用灰色GM（1,1）模型对各个子序列进行拟合。实验证明，基于灰色GM（1,1）模型与重要点的时间序列分段算法能够以更少的拟合误差，实现序列的压缩。

GM（1,1）模型；重要点；时间序列；分段表示

0 引言

时间序列作为数据库中的一种数据形式，在商业、气象、工程等领域普遍存在。时间序列数据均有“高维”、“海量”等特点，对其直接分析或处理的难度较大。因此，需要对时间序列进行降维，目前分段算法主要有限制分段数、限制分段误差以及提取特殊点三种类型。提取特殊点的分段算法主要有界标模型法、边缘点分段法、重要点分段法[1]。采用特殊点的提取方法，能够尽可能较好地保留序列的全局特征的同时保持序列局部性质。目前较多文献使用线段表示各子序列。线性的表示方式比较简单直观，但在现实生活中，采用线性的表示方式会造成较大的数据误差，因此采用曲线的表示方式更具有现实意义。目前有采用二次回归以及多项式的表达式，但这些方法需要较大的计算量，有时表示方法不合适时，会降低拟合效果。灰色GM（1,1）模型建模方法简单，且具有单调性，易于后续子序列的处理；模型又具有曲线的性质，相对线性拟合方法，能有更好的拟合精度。本文首先采用重要点分段法确定时间序列的分段数，之后利用灰色GM（1,1）模型对各子序列进行拟合，提出基于重要点与灰色GM（1,1）模型的时间序列分段算法。

1 重要点定义

通过序列重要点可以将时间序列分割成若干个相对较短但不重叠的子序列，从而达到降低时间复杂度的目的。重要点分段法主要利用局部极值点进行描述，因此重要点的选择尤为重要。本文借鉴文献[2]的分割算法。该算法在固定分段点的情况下采用重要点探测技术对时间序列进行分段，能较好地描述时间序列的整体特征。相关定义如下：

定义1（时间序列）：时间序列是一系列的观测值和观测时间组成的有序集合，记为Q=(X1，X2，…，Xn)，其中点Xi的记录值为x(ti)。

定义2（重要点）：任意时间序列Q=(X1，X2，…，Xn)，对于∀Xi，i∈[1，n]，若Xi与相邻两重要点Xp与Xq连线的垂直距离di→Lpq（公式如下）最大，则Xi为序列重要点。

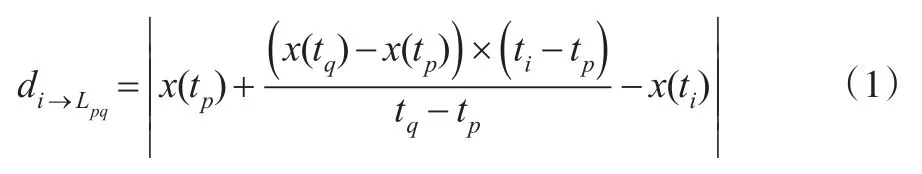
其中，点 Xp与点 Xq已经确定为序列重要点，且p＜q。如图1所示，若di→Lpq＞dj→Lpq，则 Xi为重要点，则构成(Xp，Xi)与(Xi，Xq)两个子序列。

图1序列重要点图示

重要点确定后，可根据需要对各子序列进行拟合。之后计算拟合误差以及压缩率。序列分割后的拟合误差以及压缩率的定义可参考文献[3]。

时间序列通过上述重要点确定分段数后，采用灰色GM（1,1）模型对各分段进行拟合。该模型建模方法简单，且具有单调性，易于后续对子序列的处理；模型又具有曲线的性质，相比线性拟合方法，能有更好的拟合精度。

2 灰色GM（1,1）模型

灰色GM（1,1）模型是解决特殊的实际问题而产生的，只要系统符合灰建模的条件，其建模过程的相关研究在理论和应用中都是有意义的[4]。因此对于本文采用灰色GM（1,1）模型对子序列进行拟合。相关定义如下：

定义3：设 X（0）=(x(0)(1)，x(0)(2)，…，x(0)(n))为非负序列，称 X(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))为 X（0）的一阶累加生成算子（1-AGO）序列，其中，…，n)；Z(1)=(z(1)(2)，z(1)(3)，…，z(1)(n))为 X(1)的紧邻均值生成序列，其中，

定义4：设X（0），X(1)，Z(1)如定义3所述，若ˆ=[a，b]T为参数列且满足式（5）则称GM（1,1）模型x(0)(k)+az(1)(k) =b的最小二乘估计参数列满足ˆ=(BTB)-1BTY。

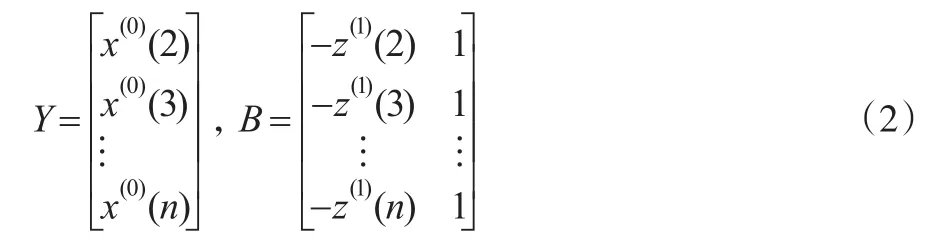
定理1：设Y，B，aˆ如上所述，uˆ=(BTB)-1BTY，则有：

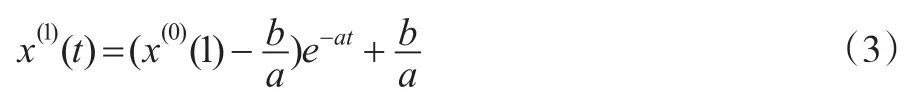
（2）灰色微分方程 x(0)(k)+az(1)(k)=b的时间响应式为：

其中k=1，2，…，n。

（3）还原值为：

其中k∈[2，n]。

因此本文采用指数序列灰色GM（1,1）模型对时间序列的各子序列进行拟合，在重要点分段前提下，实现对时间序列的数据压缩，并尽可能保留原始序列的数据特征。

3 算法描述

根据以上定义，提出基于重要点与灰色GM（1,1）模型时间序列分段算法，简记为GMPR-IP。算法步骤如下：

算法输入：时间序列Q=(x (t1)，x(t2)，…，x(tn))，分段数num

算法输出：GMPR-IP

算法步骤如下：

（1）以第一个点X1与最后一个点Xn为重要点IPs和IPe。时间序列端点序列为queue=[1，n，ε1，ip，comp，a，b]。其中，1表示子序列的起点，n表示子序列的终点，ε1表示该子序列进行拟合后的平均拟合误差，ip判断该子段是否为目标子序列，取值为0或1，comp判断该子段是否已经处理过，取值为0或1，a，b为模型拟合参数。

（2）判断queue中，各子段是否已经都处理过，如果有未处理子段，即某子段对应的comp=0，进入步骤（3）；如果已经都处理完，即queue各子段对应的comp均为1，则进入步骤（4）。

（3）在queue中comp=0的各行中，提取平均拟合误差εi最大的子序列xi。如果分段数不小于num，则该子序列对应的，ip=1，comp=1；否则，利用重要点分段算法确定该子序列间的下一个重要点，将子序列分成两个更小的子序列xk与xk+1，利用定理1所述灰色GM（1,1）模型进行序列拟合计算平均拟合误差εk+1，εk+2，将各子段信息加入对列queue中，并令xi在queue中的comp=1。

（4）取 queue中ip=1的各行构成重要子段对列ip_queue。

（5）利用ip_queue中模型参数获得序列的拟合值，计算序列整体拟合误差以及压缩率。

4 仿真实验及分析

为了测试本文方法的有效性，本文在一台硬件配置为2.0GHzCPU、2GB内存，软件配置为Windows XP的电脑上，采用MATLAB 7.0进行实验。

算例：实验采用Keogh等人提供的实际数据集[5]，数据集长度见表1。

表1 Keogh等人提供的实际数据集

文献[6]介绍的分段表示算法对应各数据集的拟合误差见表2。各参考算法中，IP算法整体拟合效果最好。本文所提GMPR_IP算法在同等80%压缩率下的数据拟合误差最小。整体拟合效果最理想。表2中同时列出GMPR_IP算法在压缩率为85%，90%，95%时的拟合误差。从表中数据可知，随着压缩率的增加，拟合误差逐渐变大。

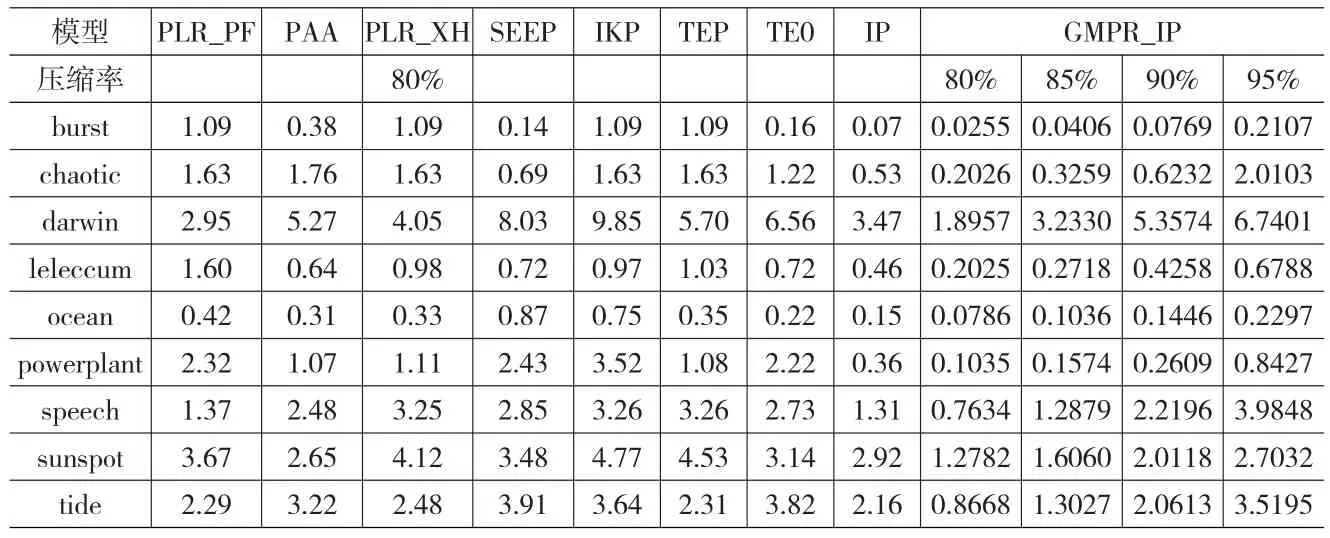
表2 GMPR_IP算法在不同压缩率下的拟合误差

5 结束语

重要点分段算法是通过搜索的方式提取序列的特征点。本文将时间序列的部分重要点作为初始分割点，对分割后的序列采用灰色GM（1,1）模型进行拟合。利用重要点分段算法可以保留轨迹局部特征，灰色GM（1,1）模型能够以曲线的形式减少拟合误差，因此本文算法同其他分段表示方法相比具有更好的压缩效果。

[1]程敏,翁宁泉,刘庆,孙刚,陈小威.基于时间序列分段的气象数据压缩算法[J].计算机系统应用,2014,23(8).

[2]陈然，戴齐.基于重要点的时间序列固定分段数分段算法[J].计算机技术与发展，2011，21（9）.

[3]詹艳艳，徐荣聪，陈晓云.基于斜率提取边缘点的时间序列分段线性表示方法[J].计算机科学，2006,33（11）.

[4]刘思峰，党耀国，方志耕，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2010.

[5]Keogh E,Folias T.The UCR Time Series Data Mining Archive[EB/ OL].http://www.cs.ucr.edu/～eamonn/TSDMA/index.thml.2009.

[6]廖俊，周中良，寇英信，罗寰.一种基于重要点的时间序列分割方法[J].计算机工程与应用，2011,47(24).

（责任编辑/浩 天）

N941.5

A

1002-6487（2016）24-0028-03

国家自然科学基金青年项目（61300104）；福建省自然科学基金资助项目（2013J01230）

江艺羡（1983—），女，漳州龙海人，博士研究生，研究方向：灰色系统、人工智能、数据挖掘。