双调谐液体柱形阻尼器及其基本动力性能*

闫维明， 倪 铭， 王 瑾

(北京工业大学工程抗震与结构诊治北京市重点试验室 北京, 100124)



双调谐液体柱形阻尼器及其基本动力性能*

闫维明， 倪 铭， 王 瑾

(北京工业大学工程抗震与结构诊治北京市重点试验室 北京, 100124)

借鉴被动调谐质量阻尼器(tuned mass damper,简称TMD)和调谐液体柱形阻尼器(tuned liquid column damper, 简称TLCD)各自的优缺点，结合土木工程结构减震装置的经济性和适用性，提出了一种双调谐液体柱形阻尼器(doubly tuned liquid column damper,简称DTLCD)，建立了简谐激励作用下单自由度DTLCD控制体系(DTLCD-SDOF)的运动方程，推导了其动力反应放大系数。提出了针对DTLCD的调优策略及优化评价函数，通过相关算法获得DTLCD-SDOF系统的参数优化程序，并利用该程序得到了DTLCD的最优参数。具体分析了不同参数对DTLCD共振峰值和调频宽度的影响，并对阻尼器阻尼参数或受控结构频率发生变化后DTLCD的鲁棒性进行了评价。对DTLCD, TMD, TLCD及DTMD的有效性和鲁棒性进行了对比分析。理论与数值研究结果表明，DTLCD的控制效果明显优于TMD和TLCD，与DTMD效果相同，并且在主结构频率的摄动方面拥有更佳的鲁棒性。事实证明，DTMD比TMD和TLCD更具工程适用性。

双调谐液体柱形阻尼器；双调谐质量阻尼器；优化设计；简谐激励；有效性；鲁棒性；振动控制

引 言

自从1909年Frahm提出TMD后，利用吸振器控制结构振动成为了一种常用的减振手段[1]。许多学者在TMD的基础上提出了很多不同类型的被动吸振器，包括多重调谐质量阻尼器(multiple tuned mass damper，简称MTMD)、调谐液体阻尼器(tuned liquid damper，简称TLD)以及TLCD。由于被动吸振器能够有效地减低结构受到地震或风荷载所引起的反应，因此已有很多吸振器被安装在了各地的高耸建筑上，如美国纽约的Citicorp Center、波士顿的John Hancock Building及澳大利亚的悉尼塔等[2]。此后，众多学者对各类被动吸振器进行了详细的研究[3-17]。结果表明， TLCD虽然能够有效地降低结构的振动，但由于TLCD本身构造的限制，其控制效果不如TMD和TLD，且控制效果和鲁棒性远不如MTMD。但由于TLCD的水箱本身能够提供阻尼，其构造比MTMD更简单。结合TLCD和MTMD的特性，笔者提出一种DTLCD及其数值优化策略与方法，对参数影响分析、有效性和鲁棒性进行系统地研究，并对DTLCD，TLCD，TMD和DTMD的有效性和鲁棒性的优劣进行对比分析。

1 DTLCD理论模型及动力方程推导

DTLCD是在传统的TLCD与主结构之间设置弹簧和阻尼的新型液体柱形阻尼器，由设置在主结构上的U形水箱以及连接水箱与主结构的滑动装置、弹簧和阻尼器构成。当主结构为单自由度时，DTLCD与主结构的理论模型如图 1所示。主结构的质量、刚度和阻尼分别为m0,k0和c0；DTLCD的质量、刚度和阻尼分别为m，k1和c1；DTLCD的宽度为b，水流运动方向总长度为L；U形水箱截面积为A；x0，x1和x2分别为主结构位移、水箱位移和水沿水流方向位移；地面加速度为ag。

由图 1的理论模型，可以建立主结构的动力方程为

(1)

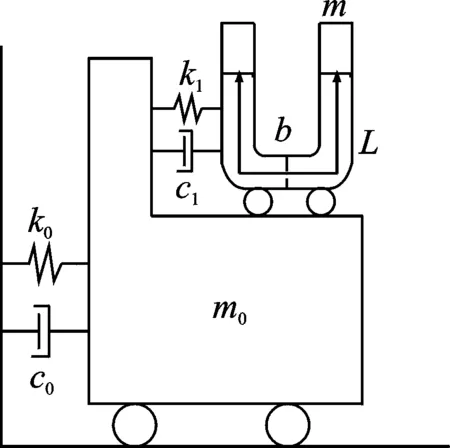
图1 单自由度结构DTLCD模型示意图Fig.1 DTLCD-single-degree-of-freedom system

水流的力平衡方程为

(2)

水箱与主结构的相互作用力平衡

(3)

联立式(1)、式(2)和式(3)得

(4)

其中：m1=ρAb；m2=ρAL；k2=2ρAg 。

对式(4)做Laplace变换可得

(5)

为了将式(5)进行化简，引入无量纲化参数质量比、频率比和阻尼比，各参数表示如下

将上述无量纲参数代入式(5)整理后得

(6)

整理式(6)得

(7)

其中

解式(7)得到结构与子质量的传递函数为

结构位移放大系数为

(8)

式(8)即为DTLCD控制下单自由度结构的动力放大系数。

2 DTLCD调优策略及优化评价函数

传统TLCD与TMD的调优策略无异，会因主结构阻尼的有无而不同：当主结构不存在阻尼时，无论TLCD本身是否设置阻尼，TLCD的最优参数均可利用定点理论得到，具体方法是将动力放大系数(DMF)-γ图中的定点高度保持一致，并使之成为曲线上的极大值点；而当主结构有阻尼时，定点理论不再适用，这时只能利用数值方法通过优化函数寻找TLCD的最优参数。常用的优化函数[2]为

Z=min{max[DMF]}

(9)

对于TLCD，要先找出不同的频率比和阻尼比下的DMF最大值，再从中找到最小的一个，其对应的参数即是最优参数。需要指出的是，这种针对TLCD的调优策略却不宜用在DTLCD上。因为TLCD的寻优对象只有U形水箱的阻尼比和频率比，但DTLCD中却有相对质量比μ′( 水流总长度L与水平段长度b的比值)、各自的阻尼比(ζ1和ζ2)以及频率比(λ1和λ2)，共5个寻优对象，利用上面的优化函数难于实现调优。因此，针对DTLCD多参数的特点，笔者提出了一种基于峰值的调优策略和优化函数。

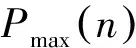
(10)

(11)

(12)

其中：式(10)为使各峰值之间相差最小的优化评价函数；式(11)为使各峰值的均值最小的优化评价函数；式(12)中的P值为两函数之和，当且仅当P1和P2均为最小值时，即P为最小值时，此时DTLCD的各参数为最优参数。

对于DTLCD-SDOF(单自由度，single degree of freedom,简称SDOF)系统，其位移放大系数响应曲线具有3个共振峰值，即n=3。

利用这个优化评价函数，笔者通过Matlab软件编写了DTLCD系统的参数优化程序，并利用该程序探索得到了DTLCD的最优参数。

3 DTLCD基本参数分析

3.1 DTLCD调优分析前提及最优参数

不失一般性，在利用程序寻找DTLCD最优参数之前，给定结构阻尼比ζ0=0.02，DTLCD总质量比μ=0.05，定义m1和m2的相对质量比μ′=μ2/μ1(即宽高比L/b)。综合考虑分析耗时和优化参数的实际可操作性，对参数寻优的范围进行了限制，阻尼比的范围限制在0～0.3之间。

在以上的分析前提下，利用程序探索得到了DTLCD的全局最优参数μ′=2.82,ζ1=0,ζ2=0.26,λ1=1.6,λ2=0.89。

下面具体各参数的分析将以此全局最优参数为参照点，比较某个参数固定后得到的条件最优参数。全局最优参数是全部参数(μ′，ζ1，ζ2，λ1和λ2)都参与搜寻后得到的最优参数，与之相对应，条件最优参数则是固定某个参数后搜寻到的最优参数，所以条件最优参数可能和全局最优参数下得到的某些结论相冲突，但并不是说条件最优参数就没有意义，它可以描述某个参数对于DTLCD系统的影响。

3.2 水箱的阻尼比ζ1

在待优化的5个参数中，下层TLCD的阻尼比ζ1有其独特的作用和特征，对DTLCD的有效性有较大的影响。图 2给出了不同阻尼比和质量比下主结构DMF最大值随ζ1变化的趋势。

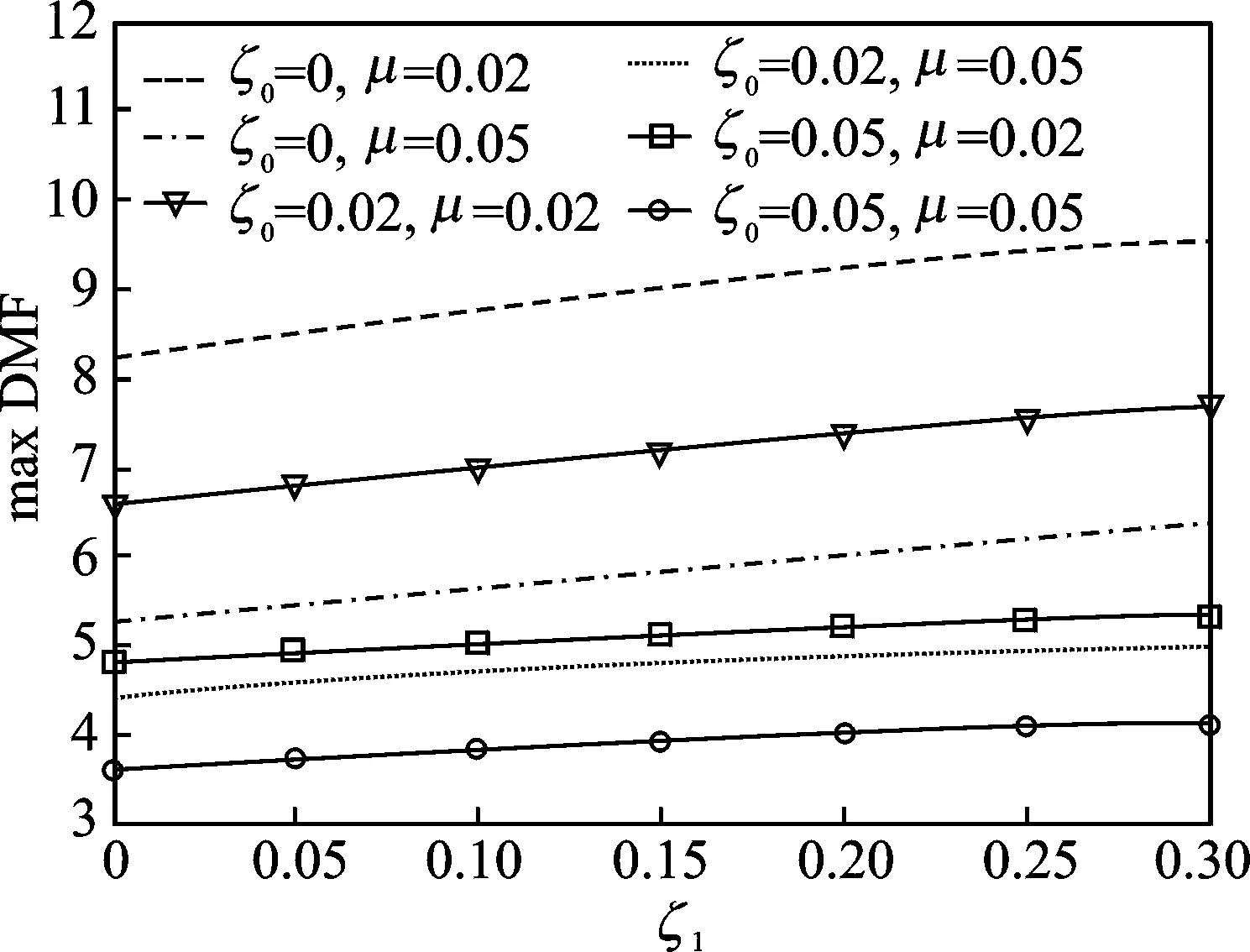
图2 ζ1变化趋势图Fig.2 Trends of ζ1

由图 2可知，DTLCD在主结构阻尼比分别为0，0.02，0.05和吸振器总质量比分别为0.02，0.05时，最大的DMF峰值都随着ζ1的增大而单调增大，即最大的DMF峰值在ζ1=0时取值最小，主结构的动力反应最小。6条曲线相同的单调性证明，对于不同阻尼比的受控结构和不同质量比的DTLCD，ζ1的影响是一致的。

另外，由图 2中的6条曲线可知，在主结构阻尼比和吸振器总质量比分别相同时，主结构阻尼比对最大DMF峰值的影响更大，相比质量比增大对最大DMF峰值的降低，其效果更加明显。但这是吸振器设计中的不可控因素，增大吸振器总质量比能够接近于主结构阻尼比增大的效果，这是设计中可以做到的。

总之 ，无论主结构阻尼比和DTLCD总质量比取何值，DTLCD系统ζ1的全局最优参数均为零，而吸振器总质量比增加后其减振效果不如主结构阻尼比的增加，这两个规律与双重调谐质量阻尼器(doubly tuned mass damper,简称DTMD)是极为一致的，而在TLCD上则没有体现。

3.3 水流的阻尼比ζ2

ζ2对DTLCD系统的影响见表 1。表 1中均为固定ζ2后程序找到的条件最优参数，其中第6行为全局最优参数。

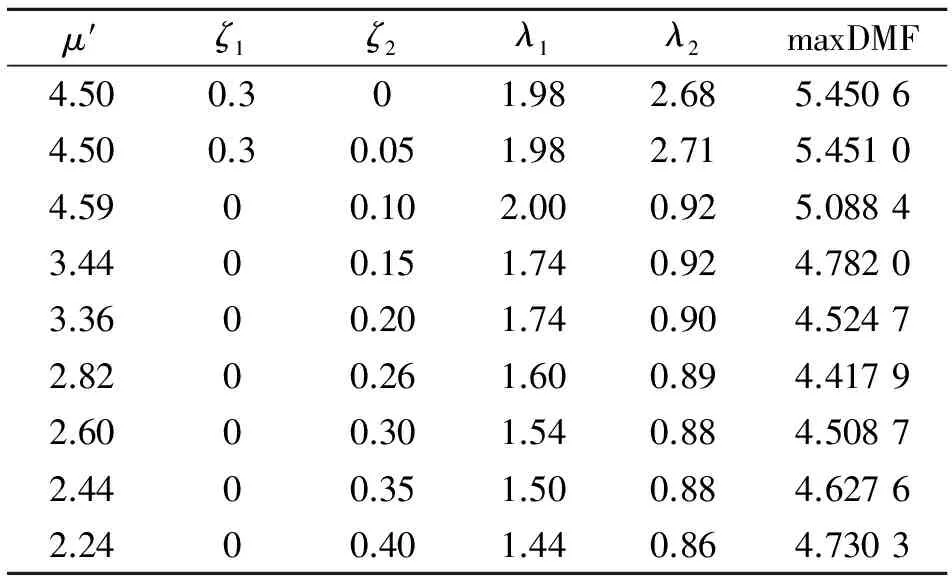
表1 随ζ2变化的条件最优参数

由表 1可以看到，ζ2以步长0.05由0增加到0.4的过程中，其他参数呈现出一起单调变化的规律。当ζ2分别为0和0.05时，两者的条件最优参数十分接近，最大DMF峰值也相差不多，可以说明较小的ζ2对DMF的影响都十分接近，也不是全局最优参数的取值范围。但是在ζ2从0.1增加的0.4的过程中，其他参数则表现出一致的变化规律，μ′ ，λ1和λ2随之单调递减，ζ1则一直为0，最大DMF峰值经历了一个先降低到最小值后增大的过程。

图 3展示了主结构动力放大系数在不同的ζ2下随频率比γ变化的曲线，参数皆取自表 1中的条件最优参数。

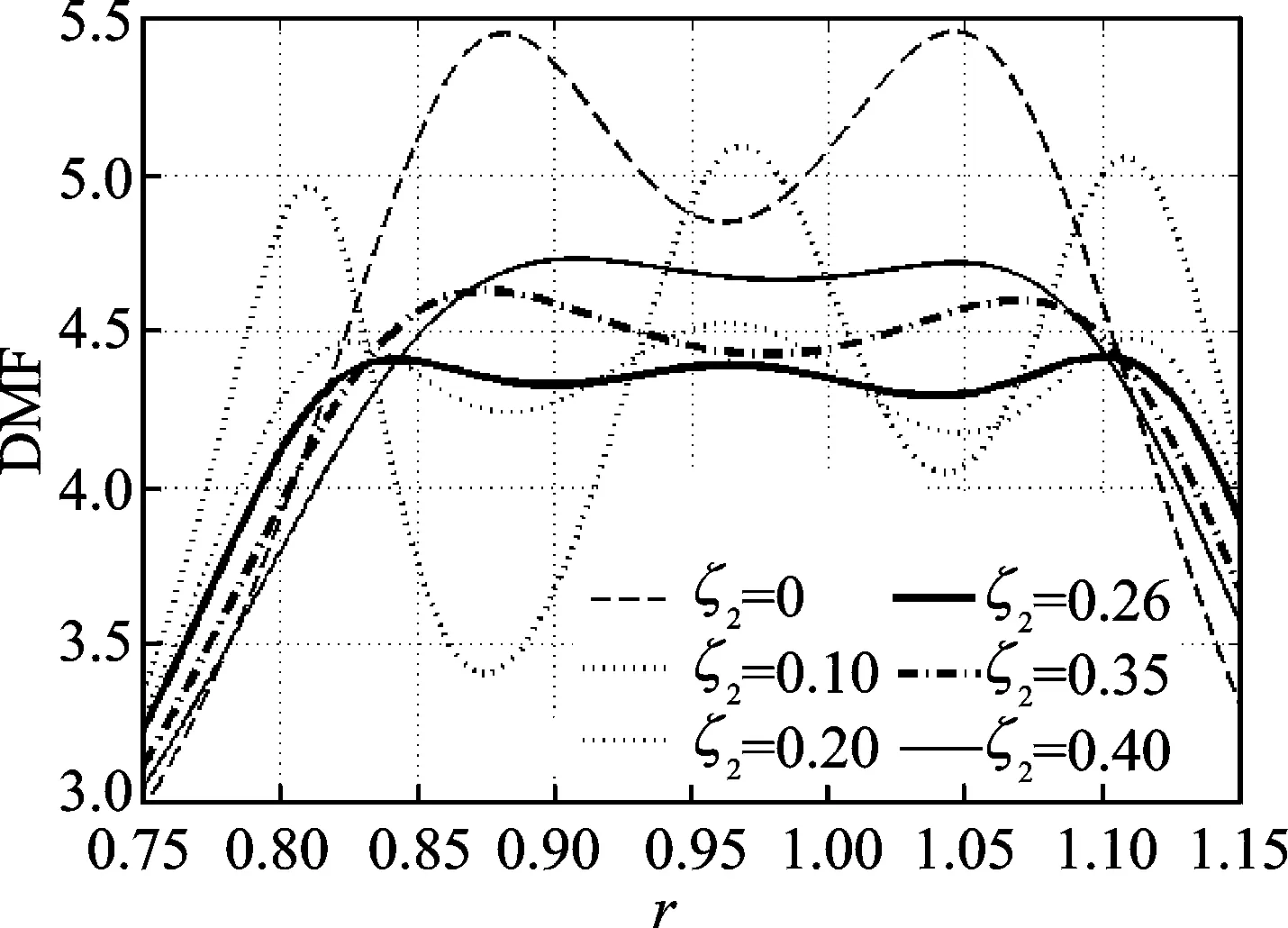
图3 不同ζ2下的主结构响应曲线Fig.3 Frequency response curves of structure for different ζ2

由图 3可以看到,在ζ2过大或者过小时(ζ2=0，0.35,0.40),DMF曲线都只有2个峰值，这是因为当阻尼比过大会抑制DTLCD中水流与水箱之间的共振，使其不能很好地耗散主结构的振动能量；ζ2过小使得ζ1又过大，共振和能量耗散也被抑制了。另外，当DMF曲线为两峰值时其调频宽度都小于三峰值时的调频宽度，说明调频宽度对阻尼比的变化也是比较敏感的。在ζ2增大过程中，当ζ2小于全局最优值时，峰值大幅降低到最小值，峰值对较小的ζ2更敏感；当ζ2大于全局最优值时，峰值缓慢增加，较大的ζ2对峰值影响较小，这是因为较大的阻尼比对总体振动的抑制要优于较小的阻尼比。

总之，当ζ2≤0.1时不同的阻尼比对峰值的影响十分接近，而在ζ2>0.1时其他条件最优参数会随着ζ2的增大单调变化，过大或是过小的ζ2都无法有效地抑制主结构的共振和能量的耗散，调频宽度也无法达到最优效果。因此，存在一个最优的ζ2使得DMF峰值最小。

3.4 相对质量比μ′(宽高比L/b)

相对质量比μ′的实质是水流总长度L与水平段长度b的比值，这个比值不能过小，否则会造成U型管竖向长度不足，进而水柱晃动使得竖管中出现完全无水的现象，这将破坏U型水箱中水运动的计算模型，从而达不到设计预定的减振效果。

μ′对DTLCD系统的影响见表 2。表 2中均为固定μ′后程序找到的条件最优参数，由于上面提到的原因，故表中的μ′由2递增至7，其中第3行为全局最优参数。

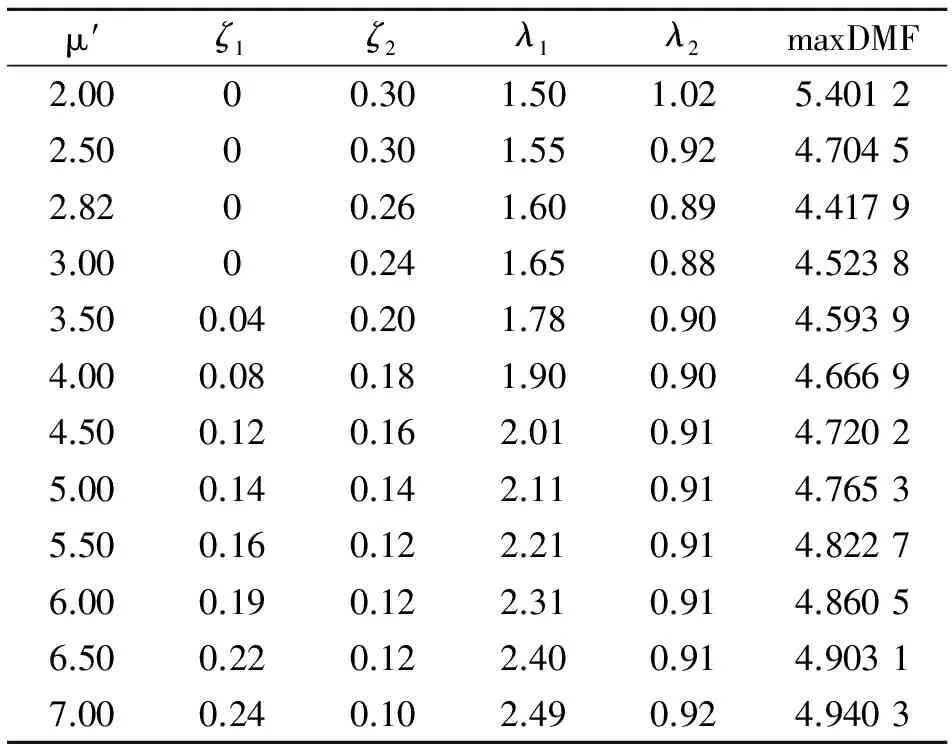
表2 随μ′变化的条件最优参数表

由表 2可知，μ′自2以步长0.5增加到7的过程中，其他参数随之单调变化，其中ζ1和λ1是单调递增，ζ2和λ2是单调递减，最大DMF峰值则经历了降低到最小值后再逐步增大的过程。另外，在μ′大于2.5之后，最大DMF值都能很好地控制在5以下，只有μ′=2时为5.401 2，说明对于DTLD来说，过小的相对质量比会对控制效果造成不良影响，这与TLD的规律不同，因为TLD要求宽高比L/b的比值越小越好，而DTLD则要求一个适当的相对质量比。

图 4给出了主结构的动力放大系数在不同的μ′ 下的变化，参数皆取自表 2中的条件最优参数。

图4 不同μ′下的主结构响应曲线Fig.4 Frequency response curves of structure for different μ′

由图 4可知，在μ′由2增加到最优值2.82，再增加到7的过程中，当μ′小于最优值时峰值下降速度很快；但μ′大于最优值时，峰值的增长则相对缓慢。另外，在μ′=2时，DMF曲线值有2个峰值，说明μ′偏小时不利于水流与U型管之间的共振，造成无法有效耗散主结构的振动能量，控制效果变差。而当μ′=3.5时，DTLCD的控制效果相对全局最优参数来说增大的并不多，其调配宽度甚至还大一点，这说明在某些特殊的情况下，比全局最优参数稍大一点的相对质量比仍然能够很好地控制主结构振动。

总之，与TLCD中宽高比L/b越小越好不同，DTLCD需要一个适当的相对质量比使得DMF峰值最小，且过小的相对质量比会使得DTLCD的控制效果大大降低。

4 DTLCD鲁棒性分析

4.1 DTLCD阻尼系数的变动

TLCD系统中的阻尼通常取决于管道中不同开洞率的隔板以及不同密度的液体，不同密度的液体在通过开洞率不同的隔板时会产生不同的阻尼。但是，灌注液体密度容易发生变化，导致TLCD系统提供的阻尼比发生变化。因此，笔者以全局最优参数为基准等倍变化，比较DTLCD阻尼系数变动后的控制效果。由于阻尼系数与阻尼比成正比，所以文中直接以无量纲化参数阻尼比为研究对象。另外，全局最优参数中TLCD与主结构之间的阻尼比为0，因此可以不设置阻尼器，故阻尼比的变动只涉及到U型管本身的阻尼比ζ2变化。

由图 5可知，以全局最优参数为基准，阻尼比在0.6～1.8倍范围内，DTLCD的控制效果仍然维持在较优的水平，主结构的反应也没有被过度放大。对于0.2ζ2与3.0ζ2，后者明显控制效果好于前者，说明DTLCD在阻尼系数变动方面的鲁棒性上，对阻尼系数降低更为敏感，控制效果也由此变得较差，而对阻尼系数的变大则能维持在可接受的范围。

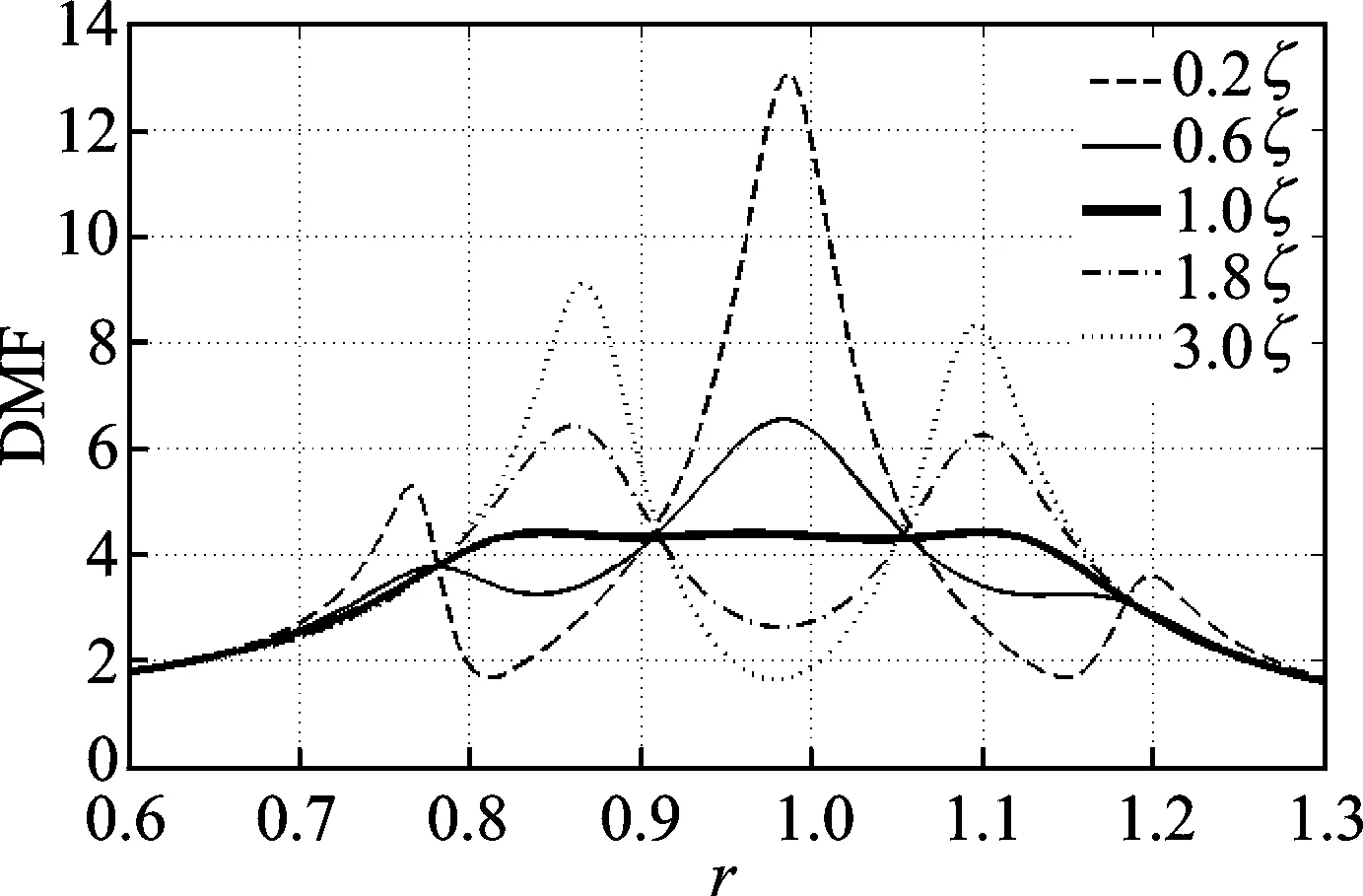
图5 阻尼比变动情况下的主结构响应曲线Fig.5 Frequency response curves of structure for different damping ratio of DTLCD

4.2 主结构频率的变动

传统TMD鲁棒性差主要体现在两点，调频宽度小以及对主结构参数变化十分敏感。由于TLCD的原理与TMD一致，所以TLCD也有同样的鲁棒性问题。DTLCD系统在TLCD与主结构之间加入弹簧后，形成双调谐的效果，其固有频率在主结构的共振峰值附近分散开来，因此即使主结构频率发生改变，DTLCD仍能发挥作用，从而缓解因固有频率变动带来的控制效果的降低。一般来说，固有频率的变化相当于刚度的变化，图6为主结构刚度成倍变化后的DTMD的控制效果。

图6 主结构刚度变化后的响应曲线Fig.6 Frequency response curves of structure for different stiffness

由图 6可知，以原刚度为基准的DMF曲线，在刚度衰减时峰值偏向左侧，在刚度增大时峰值偏向右侧，这与DTMD的规律是一致的，与MTMD相反。但无论刚度是衰减还是增大，都经历了由三峰逐渐变为单峰、峰值增加、调频宽度减小的过程，这个过程与众多吸振器是一致的。

5 DTLCD与TLCD的性能比较

本节将对不同吸振器的有效性及鲁棒性进行比较。比较对象中各吸振器的主结构与前面DTLCD主结构的基本动力特性相同。各吸振器的参数均为程序探索得到的全局最优参数，其中TLCD的参数如下：质量比为0.05；阻尼比为0.13；频率比为1.04；相对质量比为1.214。TMD的参数如下：质量比为0.05；阻尼比为0.14；频率比为0.963 5。DTMD为双调谐质量阻尼器，即主结构上有2个串联的质量块，其参数如下：相对质量比为0.13；阻尼比为0和0.24；频率比为1.01和0.89。图7是4种吸振器与原结构的控制效果比较。

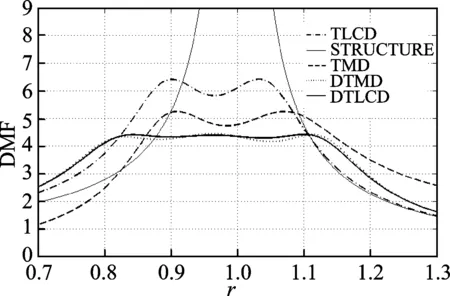
图7 4种吸振器与原结构的控制效果比较Fig.7 Frequency response curves of structure for four different mass dampers

由图 7可知，与原结构相比，TMD将主结构的共振峰值降低到了5.2左右，调频宽度大约为0.16。由于宽高比L/b的限制，TLCD将主结构的共振峰值降低到了6.5左右，调频宽度大约为0.14，控制效果比TMD要差。DTLCD与DTMD两者的曲线基本相同，控制效果比TLCD和TMD大大提高，共振峰值为4.4，比TLCD降低32.3%，比TMD降低15.4%，调频宽度为0.3，比TLCD增大114.3%，比TMD增大87.5%，其控制效果显著。由此可见，DTLCD和DTMD的共振峰值和调频宽度基本一致，且曲线基本重合，这是由两者的理论模型相近造成的。总之，双调谐吸振器的控制效果要优于单调谐吸振器。

对于吸振器，其鲁棒性体现在经过最优化调谐后其控制效果在种种变化因素的作用下仍然能够维持稳定。图8为主结构动力放大系数最大值随吸振器中单个TMD阻尼系数变化的曲线，变动的基准均为对应吸振器的全局最优参数，故1.0倍处的动力放大系数最大值最小。

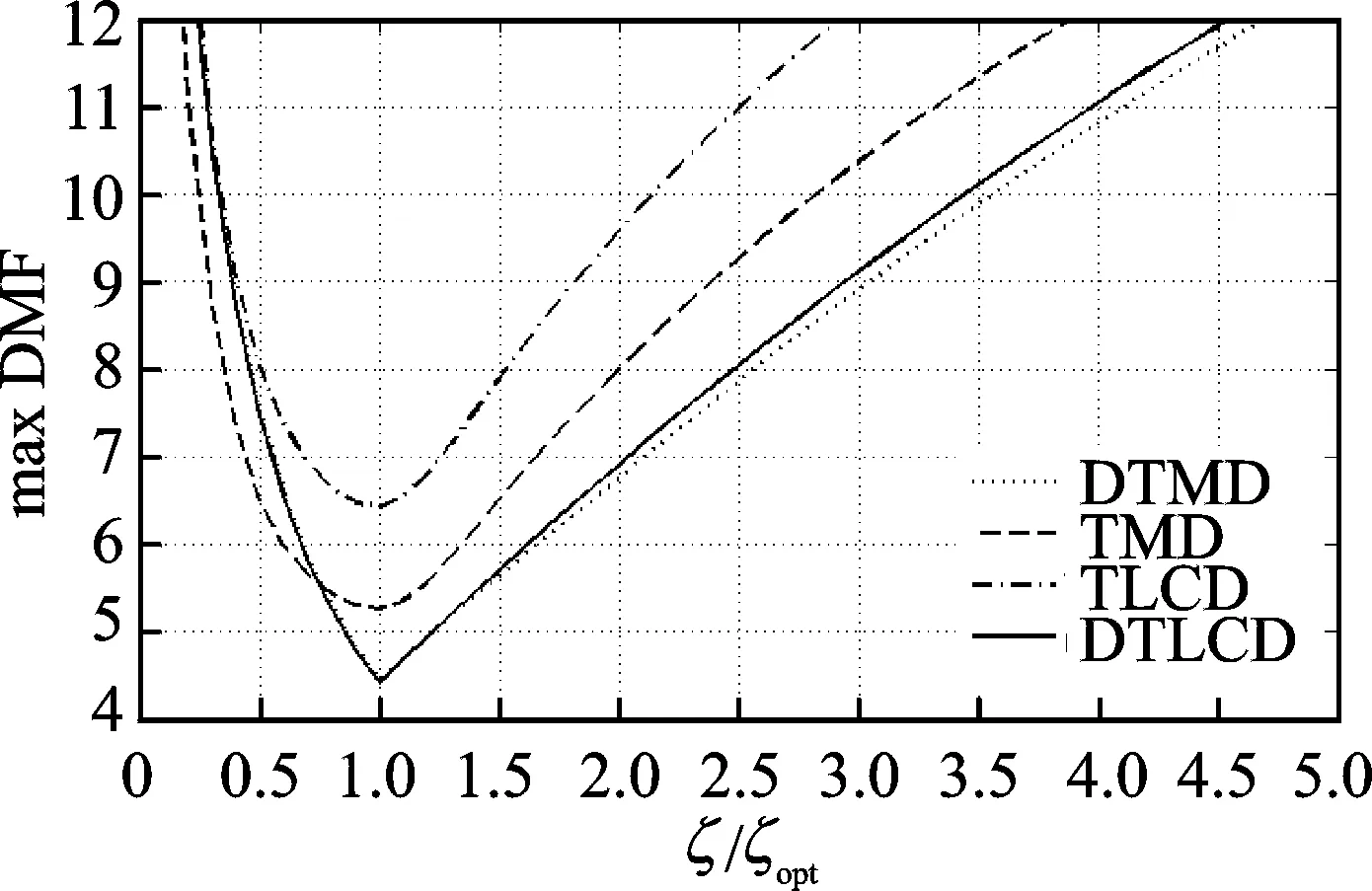
图8 4种吸振器阻尼系数变化后的比较Fig.8 Frequency response curves of structure change with damping ratio for four different mass dampers

由图 8可以看出，DTLCD与DTMD的曲线仍然基本一致，只在1.5倍的阻尼系数后比DTMD稍大。相比之下，DTLCD全程都优于TLCD，且在0.75倍阻尼系数后优于TMD。由此可见：在阻尼系数变动方面，DTLCD拥有良好的鲁棒性，且与DTMD基本一致；而在阻尼系数过小时，DTLCD对其变动比TMD更加敏感，鲁棒性变差，但仍然优于TLCD。因此可以把 DTLCD的阻尼系数设定的比最优值大一些，即使阻尼系数发生变化，动力放大系数最大值的增加也可以得到抑制。

主结构固有频率的变化也是衡量吸振器鲁棒性的重要因素。由于主结构刚度与固有频率成正比，而且主结构的刚度变化更加直观，故笔者利用主结构刚度的变化来代替固有频率的变化。图9为4种吸振器作用下主结构动力放大系数最大值随主结构刚度变化的曲线，图中4种吸振器的参数都是相同基本动力特性下的全局最优参数。

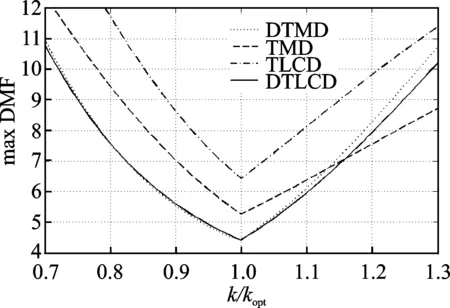
图9 4种吸振器在主结构刚度变动后的比较Fig.9 Frequency response curves of structure change with stiffness for four different mass dampers

由图 9可以看出，在刚度减小的区域，DTLCD与DTMD两者的曲线一致；但在刚度增大的区域，DTMD的动力放大系数最大值逐渐大于DTLCD，说明DTLCD在主结构刚度变化的方面其鲁棒性优于DTMD。与剩下的两者相比，DTLCD在结构刚度变化幅度为-30%～15%内比TMD鲁棒性更好，在图中全程范围内都优于TLCD。总之，对主结构频率的摄动而言，DTLCD的鲁棒性对比TMD和TLCD是有较明显的优势，而与DTMD相比效果相近，在刚度增大范围内则略优。

就鲁棒性的两个方面来说，主结构频率的摄动显然更为重要，因为阻尼系数是一个可以调节的参数，能通过重新调试或者更换阻尼系数变动的阻尼器来解决。相比之下，主结构频率本身就存在不便测量和控制的特点，而且一旦主结构频率发生摄动，工程上也没有有效的方法可以解决这个问题。因此可以认为，DTLCD的鲁棒性比TMD和TLCD更好，与DTMD基本一致。

6 结 论

1) DTLCD系统存在一个最优的相对质量比(宽高比)、阻尼比使得结构的反应最小。其中，无论主结构阻尼比和DTLCD质量比取何值，DTLCD系统ζ1的全局最优参数都是零。

2) 全局最优参数条件下，DTLCD的有效性比TLCD和TMD更优。DTLCD控制下结构的动力反应系数最大值相比TMD和TLCD控制下结构的动力响应分别降低了15.4%和32.3%。DTLCD的调频宽度比TMD和TLCD分别增大了87.5%和114.3%，对高阶振型的控制效果大大增加。DTLCD的控制效果与DTMD基本相同。

3) 当阻尼器的阻尼系数发生摄动时，DTLCD的鲁棒性与DTMD相同，在大部分情况下优于TMD，并显著优于TLCD。在更为重要的主结构固有频率摄动方面，DTLCD的鲁棒性优于TMD和TLCD。

4) 综合比较DTLCD，TMD和TLCD的有效性、鲁棒性和实用性，结果表明DTLCD与DTMD有相同的特性，且更具工程适用性。

[1] Rana R, Soong T T. 调谐质量阻尼器的参数研究与简化设计[J]. 世界地震工程, 1998, 14(4):91-107.

Rana R, Soong T T. Parametric study and simplified design of tuned mass dampers[J]. World Information on Earthquake Engineering, 1998, 14(4):91-107.(in Chinese)

[2] 背户一登. 结构振动控制[M].北京:机械工业出版社, 2011:1-40.

[3] Gao H, Kwok K C S. Optimization of tuned liquid column dampers[J]. Engineering Structures, 1997, 19(6):476-486.

[4] 阎石,李宏男,等. 可调频调液柱型阻尼器振动控制参数研究[J]. 地震工程与工程振动, 1998, 18(4):96-102.

Yan Shi, Li Hongnan, et al. Vibration control parameters research on system with adjusted frequency and tuned liquid column damper [J]. Journal of Earthquake Engineering and Engineering Vibration, 1998, 18(4):96-102.(in Chinese)

[5] Xu Kangming, Igusa T. Dynamic characteristics of multiple substructures with closely spaced frequency [J]. Earthquake Engineering and Structural Dynamics,1992,21:1059-1070.

[6] 李春祥,韩兵康,杜冬，等. 结构双重调谐质量阻尼器(DTMD)控制策略研究[J]. 土木工程学报, 2005, 38(5):1-9.

Li Chunxiang, Han Bingkang, Du Dong. Control strategy of double tune mass dampers for structures[J]. China Civil Engineering Journal, 2005, 38(5) :1-9.(in Chinese)

[7] 背户一登. 动力吸振器及其应用[M].任明章，译.北京:机械工业出版社, 2013:1-50.

[8] Hiroki Y, Napat H. Fundamental characteristics of multiple tuned mass dampers for suppressing harmonically forced oscillations [J]. Earthquake Engineering and Structural Dynamics,1993,22:51-62.

[9] Soong T T, Dargush G F. Passive energy dissipation systems in structural engineering[M]. New York:John Wiley & Sons, 1997:1-25.

[10]翟伟廉，李肇胤,李桂青，等. U形水箱对高层建筑和高耸结构风振控制的试验和研究[J]. 建筑结构学报,1993, 14(5):37-44.

Zhai Weilian, Li Zhaoyin, Li Guiqing,et al. Experiment and research on control of wind vibration responses of tall buildings and lofty structures by U-shape water tank [J]. Journal of Building Structures,1993, 14(5):37-44.(in Chinese)

[11]闫维明，纪金豹，蒋华戈,等. 新型悬吊式TMD及其在某标志塔风振控制中的应用[J].建筑结构学报,2010, 31(2): 55-60.

Yan Weiming, Ji Jinbao, Jiang Huage. A new type pendulous TMD and its application on a tower for wind-induced vibration control [J]. Journal of Building Structures, 2010, 31(2): 55-60.(in Chinese)

[12]曾胜，任意，程涛涛,等.利用调谐质量阻尼器进行管路系统减振[J].振动、测试与诊断,2012,32(5):823-826.

Zeng Sheng, Ren Yi, Cheng Taotao,et al. Vibration suppression of pipe system with tuned mass damper[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):823-826.(in Chinese)

[13]Tanuja P B, Radhey S J. Dual-layer multiple tuned mass dampers for vibration control of structures[J]. International Journal of Advanced Structural Engineering, 2010, 2(2): 91-113.

[14]Daniel Y, Lavan O, Levy R. Multiple-tuned mass dampers for multimodal control of pedestrian bridges[J]. Journal of Structure Engineering, 2012, 138: 1173-1178.

[15]Clarence W de S. Vibration damping, control, and design [M].LLC, Boca Raton: CRC Press, Taylor & Francis Group, 2007:1-5,6-17.

[16]龙复兴,张旭,顾平，等. 调谐质量阻尼器系统控制结构地震反应的若干问题[J]. 地震工程与工程振动, 1996, 16(2):87-94.

Long Fuxing, Zhang Xu, Gu Ping,et al. Problems in seismic responses of structures under the control of tuned mass dampers[J]. Journal of Earthquake Engineering and Engineering Vibration, 1996, 16(2):87-94.(in Chinese)

[17]欧进萍,王永富. 设置TMD、TLD控制系统的高层建筑风振分析与设计方法[J]. 地震工程与工程振动, 1994,14(2):61-75.

Ou Jingping, Wang Yongfu. Wind induced vibration analyses and design methods of tall buildings with tuned mass dampers[J]. Journal of Earthquake Engineering and Engineering Vibration, 1994,14(2):61-75.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.06.022

*国家自然科学基金资助项目(51378039; 91315301-03)

2014-09-09；

2014-11-10

TU317+.1; TU352.1

闫维明，男，1960年9月生，研究员。主要研究方向为工程振动与智能控制、结构检测与健康监控、结构抗震与减震。曾发表《新型悬吊式TMD及其在某标志塔风振控制中的应用》(《建筑结构学报》2010年第31卷第2期)等论文。 E-mail:yanwm@bjut.edu.cn