多通道式液压衬套动态特性的测试与计算分析*
杨超峰, 殷智宏, 吕兆平, 段小成, 上官文斌,
(1. 华南理工大学机械与汽车工程学院 广州,510640) (2. 上汽通用五菱汽车股份有限公司 柳州,545007)(3. 宁波拓普集团股份有限公司 宁波,315800)
多通道式液压衬套动态特性的测试与计算分析*
杨超峰1, 殷智宏1, 吕兆平2, 段小成3, 上官文斌1,3
(1. 华南理工大学机械与汽车工程学院 广州,510640) (2. 上汽通用五菱汽车股份有限公司 柳州,545007)(3. 宁波拓普集团股份有限公司 宁波,315800)
制作了不同结构类型液压衬套的实验样件,测试得到其静、动特性的变化特性,并对比分析了不同结构液压衬套的作用机理。建立了多惯性通道-多节流孔式液压衬套的集总参数模型,给出了其动刚度和滞后角的计算分析公式和滞后角峰值频率的计算公式,计算结果与实验值一致,验证了计算模型的正确性。分析了多通道式液压衬套的动特性与通道数目数量及其截面形状的关系。所采用的分析方法及结论,可为液压衬套的初级阶段的设计及选型提供参考。
液压衬套; 多通道; 集总参数模型; 测试分析; 参数识别; 动态特性
引 言
为了控制来自发动机、变速器、路面、结构共振及车轮的不平衡等干扰激励引起的振动及噪声,提高车辆的操纵稳定性,液压衬套在车辆悬架与副车架中得到了广泛的应用[1-4]。Sauer等[1]建立了一种具有惯性通道与旁通道的液压衬套模型,但并没有给出具体的仿真结果。上官文斌等[2]建立了一个线性的单惯性通道式液压衬套集总参数模型,并实验验证了模型的正确性。Chai等[3]建立了一个概念性液压衬套的物理模型,并采用手动控制的方法改变不同流道之间的组合对这种液压衬套进行了分析。但他们并没有在频域范围内对流体通道的数量与液压衬套动态特性之间相互的影响关系进行研究。在液压衬套的特性中,滞后角峰值所对应的峰值频率是衬套的一个重要性能参数。单通道的液压衬套模型可看作单自由度的动力吸振器。在频域内,其滞后角的带宽较窄,滞后角的峰值频率一般较低(<50 Hz)。仅通过调整惯性通道的长度及横截面积,并不能得到理想的滞后角峰值频率。此外,液压机构的阻尼容易受到使用环境的影响,而多重动力吸振器的鲁棒性能更好[5],所以采用多通道式液压衬套更有利于振动的衰减。对单惯性通道集总参数模型的研究已经较为成熟[2,6-7]。Lu等[8]只是对窄带的双惯性通道式液压衬套进行了分析。
笔者主要对径向型液压衬套在低频、大振幅激励下的动特性进行分析,设计并试制了不同结构类型的多通道式液压衬套样件,测试得到其静、动态力学特性,验证了不同结构试件的一致性。建立了不同结构液压衬套的集总参数模型,给出了滞后角峰值频率的计算公式。计算结果与实验值进行了对比,验证了模型的准确性。预测分析了通道的形状及数量等参数对液压衬套动态特性的影响,采用的分析方法及结论可对液压衬套进行优化设计。
1 液压衬套动态特性的测试结果与分析
1.1 实验对象
控制臂惯性通道式液压衬套沿其径向及轴向的剖面结构如图1所示,衬套的外管与内管之间的橡胶主簧与外管之间形成上、下两个液室,液室内充满乙二醇液体。两液室之间通过惯性通道或节流孔相连接,流道板与金属外管形成惯性通道或孔口通道,如图2所示。
液压衬套主要在液压工作方向提供阻尼。当内外管的相对位移发生变化时,两液室内的压力差产生波动,液体通过惯性通道在两液室内来回流动,通道内的振动液柱在运动中产生惯性阻力。可见,惯性通道式液压衬套是利用液体流动的沿程能量损失、液体与壁面的摩擦损失及局部损失损耗振动的能量,从而达到减振的目的。
当惯性通道式液压衬套受到高频激励时,由于液体的黏性,液体在惯性通道内的流动速度减慢,当达到液柱的共振频率后,通常可假设通道“锁止”,惯性通道内的液体不流动。此时,由于液体不可压缩,导致液室内的压力迅速升高,液压衬套将出现动态硬化,导致刚度增大。采用孔口式液压衬套可在高频获得较大阻尼。
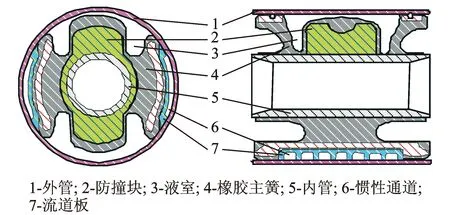
图1 液压衬套的剖面图Fig.1 The cross-sectional view of hydraulic bushing
孔口式液压衬套可分为小节流孔式及大节流孔式衬套。孔直径较小的节流式液压衬套的阻尼效应与惯性通道的阻尼效应相比较小,其主要在低频范围内起作用。孔直径较大的液柱共振式液压衬套可在较宽频率范围内得到较大的阻尼,但由于节流孔的直径较大,低频下产生的阻尼较小。笔者主要对大节流孔式衬套进行分析。

图2 液压衬套的流道板Fig.2 The runner plate of hydraulic bushing
虽然液压衬套与液阻悬置的作用机理类似,但液压衬套的两个液室均为工作液室,两液室中的压力均很大;而液阻悬置下液室的体积柔度较大,下液室内的压强与上液室内的压强相比较,一般可忽略不计。因此,液阻悬置的参数模型并不能直接用于液压衬套的分析。
液压衬套的结构及材料参数尺寸如表1所示。

表1 液压衬套的结构及材料参数尺寸
为了对不同通道结构液压衬套的静、动态特性进行测试分析,通过改变流道板可获得5种液阻减振机构的不同组合,并标识为样件HB1~HB5。具体结构如表2所示。每种样件均制作了2个样品,共制作了10个样件。通过放掉对应液压衬套内的液体,可获得对应橡胶主簧样件HB6。所采用的实验样品均在宁波拓普集团股份有限公司中试制。

表2 液压衬套样件的结构
液压衬套动态特性的测试是在MTS831弹性动态特性振动测试实验台上进行的。液压衬套的动特性通常采用动刚度与滞后角进行评价,动态实验的方法及数据处理的方式与液阻悬置动态特性测试所采用的方法类似[2,9]。本实验只对液压衬套径向的动特性进行了分析。
1.2 液压衬套静、动特性的测试结果与分析

图3 不同结构液压衬套静特性的对比Fig.3 Static characteristics of hydraulic bushings with different configurations
不同结构液压衬套特性之间的可比性是本次实验研究的前提,HB1,HB2,HB4与HB5的静态力-位移曲线如图3所示。由图3可知,当位移激励在0~3 mm范围内时,4个样件的力-位移曲线为线性,曲线的一致性较好;当位移激励大于3~4 mm范围内时,力-位移曲线为非线性,样件的曲线基本一致;当位移激励大于4 mm后,由于金属外管与防撞块相接触,力-位移曲线急剧增大。
由于样件的力-位移曲线的差别较小,最大相差为5%,在工程误差允许范围内。结果表明所制作样件的静态特性具有一致性,制作样件所采用的该批次的橡胶材料的性能一致,样件的硫化、液封等工艺具有稳定性。不同结构液压衬套在300~600 N载荷下的平均静刚度约等于462.70 N/mm。
由于相同结构形式的2个液压衬套样件的动特性实验结果对应一致,在以下的比较研究中,对同一结构的液压衬套仅列出1个样件的实验结果。
图4为不同结构液压衬套在大振幅激励下的动刚度特性。由图4可知,在大振幅激励下,HB1的动刚度在36 Hz附近出现峰值,其滞后角在13 Hz邻近出现峰值。当频率大于60 Hz后,HB1,HB3及HB6的动特性类似,表明液体产生的阻尼减小。HB2的动刚度与HB1类似,随频率的增加,HB2在12 Hz邻近出现谷值,之后在48 Hz附近出现峰值,滞后角在22 Hz邻近出现峰值。当频率大于80 Hz后,HB2,HB1及HB3的动刚度特性类似,表明通道内液体的流动性减弱,液体产生的阻尼较小。由图4可知,在大振幅激励下,HB4与HB5的动刚度只具有谷值,出现谷值点的频率分别在35 Hz与55 Hz邻近,但并没有出现峰值。HB4与HB5的滞后角分别在58与90 Hz邻近处出现峰值,两者表现为宽带特性。

图4 不同结构液压衬套的动特性Fig.4 The dynamic characteristics of hydraulic bushing with different configurations
由以上分析可见,不同结构液压衬套滞后角的带宽不同,HB1最小,HB5最大。随惯性通道的增加,液压衬套动刚度及滞后角的峰值及其对应频率增加,液压衬套可在更宽频率范围内提供阻尼。比较HB2,HB4与HB5可知,大节流孔口式通道的增加可以在高频更宽频带范围提供较大阻尼。可见,只要对液体通道的数目与尺寸进行合理的选择,就可得到理想的液压衬套动特性与激振频率的关系。
2 多通道式液压衬套的集总参数模型
假定液压衬套具有两组尺寸分别相同的液体通道,其集总参数模型如图5所示。其中:第1组通道是由n1个相同的惯性通道构成;第2组通道是由n2个相同的节流孔口式通道组成。Kr,Br为橡胶主簧的动刚度及阻尼系数;Kr为Kr1与Kr2的和;Br为Br1与Br2的和;Ap1,Ap2分别为两液室的等效活塞面积;P1(t) ,P2(t)分别为两液室内的平均波动压力;两液室的体积变形量分别用体积刚度K1及K2表征,K1,K2分别为液室体积柔度C1和C2的倒数;Qi(t),Qo(t)为流经通道的液体流量;li为惯性通道的流线长度;Ai为惯性通道的横截面积;xi(t)为液柱相对壁面的位移;内管上承受正弦位移激励为xr(t)=Xrsinωt;FT(t)为响应力。

图5 多惯性通道-多节流孔式液压衬套的集总参数模型Fig.5 Fluid system model of hydraulic bushing with multiple inertia tracks and orifice elements
图5中:Ii为惯性通道内液柱的惯性系数;Ri为Ri1及Ri2两者之和;Ri1是由于液体在惯性通道内流动的沿程损失所产生的线性阻尼系数;Ri2为由于惯性通道内液体进出通道口或弯曲通道引起的液柱流速的大小、方向或两者均发生改变所引起的非线性阻尼系数。Ii,Ri1及Ri2的定义式[11]为
(1)
其中:mi为惯性通道内液柱的质量;ξi1为与液体速度的一次方成正比的速度阻尼系数;ξi2为与液体速度的平方项成正比的速度阻尼系数。
由于Ri2的局部阻力损失所导致的阻尼为2阶非线性流体阻尼[12],而低频、大振幅激振下,惯性通道内液体的流动状态为层流[3],所以2阶非线性阻尼对系统的影响较小,可忽略不计。Ri1的定义[10]为
(2)
其中:μ为液压衬套内液体的动力黏度系数;di为惯性通道的水力直径。
由于液体流进流出通道口时横截面积的改变及管道弯曲所导致的局部阻力损失增大了液压衬套的阻尼,为了得到符合真实情况的预测值,通过引用经验系数γ进行调节。
因孔口的壁厚L与孔口水力直径do的比值约等于1,所以孔通道为薄壁孔口[13]。考虑到射流的作用,可将液体流经节流孔的流线长度等效为孔通道的长度lo。Io为孔口通道中液体的惯性系数;xo为射流液柱相对壁面的位移;Ro为Ro1及Ro2两者之和;Ro1与Ro2分别为由于液柱在孔口流动的局部损失所产生的线性阻尼系数及非线性阻尼系数。一般Io,Ro1与Ro2较难确定,通过引入经验参数,采用相同的集总参数模型对孔口式液压衬套进行分析,Io与Ro1的定义[10]分别为
(3)
其中:ρ为液体的密度;Ao为孔口的横截面积;β与ε为经验参数,当do/lo≈0时,取值分别为0.83及0.003 5;Qo为液体流过孔口的流量;co为流量系数。
co与do,lo及雷诺数Re有关[10]
(4)
设集总参数模型的状态变量为XT=[x1,x2,x3,x4]=[(P1,P2,Qi,Qo],可得到系统的动力学状态方程为

(5)
其中
(6a)
(6b)
在位移激励xr(t)下,传递到外管的力为
(7)
由式(5)~式(7),采用Laplace变换,可得多惯性通道-多节流孔式液压衬套的复刚度表达为
(8)
式(8)中
(9a)
(9b)
由图5可知,通道内液柱运动位移与流量的关系为
(10)
将式(10)与Ri2=0及Ro2=0代入式(5),可得到多惯性通道-多节流孔式液压衬套内液柱运动的微分方程
(11)
其中:X1T=(n1xi,n2xo);M,C及K分别为系统的质量矩阵、阻尼矩阵及刚度矩阵;Fm(t)为力向量矩阵。
其特征方程为
(12)
由式(12)可得到多惯性通道-多节流孔式液压衬套内液柱的共振频率fn为
(13)
由式(13)可知,系统只有1个非零的谐振频率,所以对应系统的滞后角只有1个峰值。
由以上分析可见,将流经节流孔的流线长度等效为节流孔液柱的长度,可将孔口式液压衬套视为通道长度与等效长度相等的惯性通道式液压衬套,实现了孔口式液压衬套与惯性通道式液压衬套在动力学模型上的统一,降低了建立集总参数模型的工作量,有利于底盘-悬架衬套系统的动力学计算分析。
3 液压衬套模型参数的辨识
在低频位移激励下(如1 Hz),液压衬套两液室的等效活塞面积泵液所排开或吸入的液体被同步排入或被吸入另一个液室,但并不会引起两液室间的压力差有较大的变化,所以通过液体路径传递的力对液压衬套低频动刚度的作用很小,可忽略不计。如图4所示,当频率低于5 Hz时,橡胶主簧的动刚度与液压衬套动刚度变化趋势相同,动刚度都随振幅的增大而降低。当激励频率趋于零时,在不同振幅激励下,橡胶主簧的动刚度在452.32~488.65 N/mm的范围内,而液压衬套的动刚度在501.87~505.76 N/mm之间,两者相差小于50 N/mm。可知惯性通道内的液体对动刚度的贡献较小,所以在较低激励频率下,橡胶主簧的动刚度起主要作用,可通过低频位移激励下液压衬套的动刚度识别橡胶主簧的动刚度Kr。笔者采用液压衬套橡胶主簧的动态实验结果得到不同振幅下Kr与Br的值。
由于实验样件间具有一致性,所以可采用单惯性通道式液压衬套的特性对K1及K2的参数进行识别。在大振幅激励下,单惯性通道式液压衬套的存储动刚度与损失动刚度如图6所示,两者都具有不动点(M1,M2,N1)。因存储刚度的不变特征点所对应的频率点fM2与液柱的共振频率fn1近似相等[12],K1及K2对应成比例,且Ai,ρ及li等几何物理参数已知,由实测值和式(14)可得到K1与K2的值。
(14)

图6 单惯性通道液压衬套的存储动刚度及损失动刚度Fig.6 Dynamic stiffness in-phase and out-of-phase of the hydraulic bushing
由于不变特征点附近的存储动刚度的变化曲线几乎与x轴(频率轴)垂直,不变特征点处较小的测量及辨识误差对不变特征点频率fM2的影响较小,所以采用fM2辨识fn1的精度较高,进而可对体积刚度进行识别。
由式(8)可知,随着频率的增大,单惯性通道液压衬套的存储动刚度趋近于定值,即
(15)
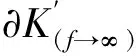
采用上述计算方法,由测试结果可见,当频率增大时,单惯性通道液压衬套的存储动刚度的值趋近于1.930×106N/m。参考表1中衬套的物理参数,辨识得到单惯性通道液压衬套的参数值:Kr为4.84×105N/m;K1与K2分别为2.31×1011和2.08×1011N/m5;Ap1与Ap2分别为1.91×10-3和1.72×10-3m2。
4 液压衬套集总参数模型动态特性的分析
由图5及式(8)可见,当设n1=1~7,n2=0时,可得具有n1个相同惯性通道液压衬套动特性的表达。随n1的增加,液压衬套动特性的变化如图7所示。由图7可知,当n1=1及n1=2,采用模型计算得到的液压衬套的动特性与单惯性通道及双惯性通道液压衬套的实测值吻合较好,表明所建立的多通道式液压衬套的集总参数模型可以用于多个相同惯性通道液压衬套动特性的计算。随着n1的逐渐增加,动刚度峰值及其所对应的峰值频率逐渐增加,滞后角峰值及所对应的峰值频率也逐渐增大,并且滞后角的带宽增加。表明随n1的增大,液压衬套可在较宽频带内提供阻尼。
当n1=2,n2=0;n1=1,n2=1及n1=0,n2=2时,由式(8)可得到对应HB1,HB2,HB4与HB5的动特性表达式,计算值与实测值的对比如图8所示。由图8可知,采用模型计算得到液压衬套的动特性与实测值吻合较好。表明所建立的具有两组相同尺寸多通道式液压衬套的集总参数模型的正确性。由于将节流孔流线长度等效为惯性通道长度,对节流孔通道内液体湍流影响估计不足及测试误差的影响,HB4的滞后角在0~35 Hz内的计算值与测试值误差较大,HB5的滞后角在0~55 Hz内的计算值与实验值误差较大。但计算值在整体频域范围内可预测液压衬套的动特性。
由式(13)所示的液柱共振频率的表达可知,n1与n2的取值不同,得到对应液压衬套液柱的共振频率不同,当设n1=1,n2=0;n1=2,n2=0;n1=1,n2=1及n1=0,n2=2时,可得到对应HB1,HB2,HB4与HB5液压衬套内液柱的共振频率,计算值与实验值的比较见表3。由表3可知,采用式(13)得到的液柱共振的频率与实验值较为接近,表明笔者估算滞后角的峰值频率的方法是可行的。

表3 液柱共振频率的对比
随着n1与n2的变化,液压衬套动特性的变化如图9所示。由图9可知,当n2=2时,随n1逐渐增大(n1=1,2,3),液压衬套的动特性变化很小,表明当频率较高时,这种具有宽带特性液压衬套的动特性受惯性通道数目改变的影响较小。当n1=3,n2=3时,动刚度的最大峰值降低,峰值频率增加,同时滞后角的峰值减小,而滞后角的峰值频率增加。令n1=0,随着n2的增大(n2=4,6),动刚度的陷波峰值及最大峰值变小,但所对应的峰值频率增大,同时滞后角的峰值有一定降低,而所对应的峰值频率增大。

图7 n1个相同尺寸的惯性通道液压衬套动特性的计算结果与实测结果对比(振幅为0.8 mm)Fig.7 Comparisons between experimental and calculated results of the dynamic characteristics of hydraulic bushing with multiple inertia tracks (amplitude is 0.8 mm)

图8 多通道液压衬套动特性计算结果与实测结果的对比(振幅为0.8 mm)Fig.8 Comparisons between experimental and calculated results of the dynamic characteristics of hydraulic bushing with multiple tracks (amplitude is 0.8 mm)

图9 液压衬套动特性随通道变化的预测Fig.9 The predicted results of the dynamic characteristics of hydraulic bushing with multiple tracks
5 结 论
1) 采用实验的方法,测试分析了不同结构形式液压衬套动特性的变化。采用对比分析的方法,对液压衬套的作用机理进行了阐述,认为随惯性通道数目的增加,液压衬套滞后角的峰值及出现峰值的频率都增大。通过改变通道的结构,可使液压衬套在较宽频率范围内具有大阻尼的特性。
2) 采用多通道-多节流孔式液压衬套的集总参数模型,对不同结构形式液压衬套的动特性及滞后角的峰值频率进行了计算,并与实验值进行了对比。计算值与实验结果相一致,验证了模型的正确性。
3) 通过改变通道的数目,分析了液压衬套动特性变化的规律。结果表明,随惯性通道数目的增加,具有n个相同尺寸多惯性通道式液压衬套动刚度及滞后角的峰值及所对应的峰值频率增大。但随惯性通道数目的增多,对具有孔口通道式多通道液压衬套的动特性的性能影响较小。随着孔口通道数目增多,动刚度的最大峰值降低,所对应的峰值频率增大。同时滞后角的峰值减小,峰值所对应的频率增大。
[1] Sauer W, Guy Y. Hydro bushings-innovative NVH solutions in chassis technology[J].SAE Technical Paper Series, 2003-01-1475.
[2] 上官文斌,徐驰.汽车悬架控制臂液压衬套动态特性实测与计算分析[J].振动与冲击,2007,26(9):7-10.
Shangguan Wenbin, Xu Chi. Experiment and calculation methods of the dynamic performances for hydraulic bushings used in control arms of a suspension[J]. Journal of Vibration and Shock, 2007, 26(9):7-10. (in Chinese)
[3] Chai Tan, Dreyer J T, Singh R. Time domain responses of hydraulic bushing with two flow passages[J]. Journal of Sound and Vibration, 2014,333(3):693-710.
[4] Miyamoto Y, Nakamura S. Study of hydro bush for reduction of harshness and road noise[J].Society of Automotive Engineers of Japan, 2005,26:33-40.
[5] 背户一登.动力吸振器及其应用[M].任明章,译.北京:机械工业出版社,2013:16-105.
[6] Lu M, Ari-Gur J, Garety J. Predication of automotive hydrobushing resonant frequency[C]∥Proceedings of the ASME Noise Control and Acoustics Division-1999. U.S.: ASME, 1999:157-159.
[7] Lu M. Study of automotive hydromount mechanism[D]. Michigan: Western Michigan University, 2001.
[8] Lu M, Ari-Gur J. Study of hydromount and hydrobushing with multiple inertia tracks[C]∥Proceedings of 2002 JSAE Annual Congress. Yokohama: JSAE, 2002:5-8.
[9] 吕振华,上官文斌,梁伟,等.液阻型橡胶隔振器动态特性实验方法及实测分析[J].中国机械工程,2003,15(2):182-186.
Lü Zhenhua, Shangguan Wenbin, Liang Wei, et al. Experimental methods and test evaluation for the dynamic characteristics of hydraulically damped rubber mount[J]. China Mechanical Engineering, 2003, 15(2):182-186. (in Chinese)
[10]Barszcz B, Dreyer J T, Singh R. Experimental study of hydraulic engine mounts using multipleinertia tracks and orifices: narrow and broad band tuning concepts[J]. Journal of Sound and Vibration, 2012,331:5209-5223.
[11]Zhang Yunqing, Shangguan Wenbin. A nnovel approach for lower frequency performance design of hydraulic engine mounts[J]. Computers and Structures, 2006, 84:572-584.
[12]Fan Ranglin, Lü Zhenhua. Fixed points on the nonlinear dynamic properties of hydraulic engine mounts and parameter identification method experiment and theory[J]. Journal of Sound and Vibration, 2007,305:703-727.
[13]林建忠,阮晓东,陈邦国,等.流体力学[M].北京:清华大学出版社,2010:102-215.

10.16450/j.cnki.issn.1004-6801.2016.06.004
*国家自然科学基金青年基金资助项目(B5130960);中央高校基本科研业务费资助项目(D2131410)
2014-11-05;
2015-01-07
TH113; U464
杨超峰,男,1981年6月生,博士。主要研究方向为液阻橡胶隔振器振动控制、车辆振动噪声分析与控制。曾发表《汽车悬架液压衬套非线性动特性的实验与建模方法研究》(《振动与冲击》2016年第35卷第3期)等论文。 E-mail:ychf8130@163.com 通信作者简介:殷智宏,女,1982年2月生,讲师。主要研究方向为汽车振动噪声分析与控制、汽车动力学、橡胶隔振、悬架系统设计与主动控制。 E-mail:mezhyin@scut.edu.cn

