瞬时湿表面波浪增阻修正方法研究

李传庆， 高玉玲， 董国祥(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

瞬时湿表面波浪增阻修正方法研究

李传庆， 高玉玲， 董国祥
(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

频域中假设入射波和船舶运动同时为简谐的情况下，由于船体表面的非线性，一个周期内瞬时湿表面上的平均佛汝德克雷洛夫(Froude-Krylo, FK)力与平均湿表面上的FK力有所不同。对此，在运用切片法计算船舶运动的基础上，进行瞬时湿表面上平均FK力的计算得到修正的船舶运动，进而计算波浪增阻，并与平均湿表面情况下的计算结果及试验结果进行对比。对比结果表明，考虑简单瞬时湿表面时，波浪增阻预报精度有所提高。

瞬时湿表面； 佛汝德克雷洛夫力； 切片法； 波浪增阻

0 引 言

基于切片法计算船舶运动时，通常在船舶平均湿表面上进行积分得到佛汝德克雷洛夫(Froude-Krylo，FK)力[1]。在时域势流理论中，通常可考虑瞬时湿表面的非线性问题。例如陈京普等[2]基于Rankine源的线性时域理论在运动方程中考虑瞬时湿影响的非线性和入射波力；秦洪德[3]基于二维频域理论，通过时域步进方式得到稳定时历，进而考虑瞬时湿表面下波浪载荷的计算。频域中假设入射波和船舶运动同时为简谐的情况下，由于船体表面的非线性，1个周期内瞬时湿表面上的平均FK力与平均湿表面上的FK力有所不同。

对此，在运用切片法计算船舶运动的基础上[4-5]，进行瞬时湿表面上平均FK力的计算，得到修正的船舶运动，进而计算出波浪增阻，并与平均湿表面情况下的计算结果及试验结果进行对比。

1 计算方法

采用切片法计算船舶的升沉纵摇运动，进而考虑瞬时湿表面情况下波浪增阻的计算。

1.1 方法原理及流程

在FK基本假设下，只需考虑入射波对船体的干扰力，无需考虑船体和运动对流场的影响，这样由入射波对船体引起的干扰力称为FK力[6]。

入射波和船舶运动同时为简谐的情况下平均湿表面与一个周期内某时刻的瞬时湿表面见图1。首先在瞬时湿表面上计算平均FK力，然后进行船舶运动的计算。为方便叙述，各个量在平均湿表面情况下的下标为0，在瞬时湿表面情况下的下标为1。考虑简单瞬时湿表面时波浪增阻修正方法计算流程图见图2，首先计算平均湿表面下船舶的运动，获得船舶运动与入射波相互作用下的瞬时湿表面；然后计算FK1力；最后迭代计算船舶运动，直至前后二次运动差别满足要求。

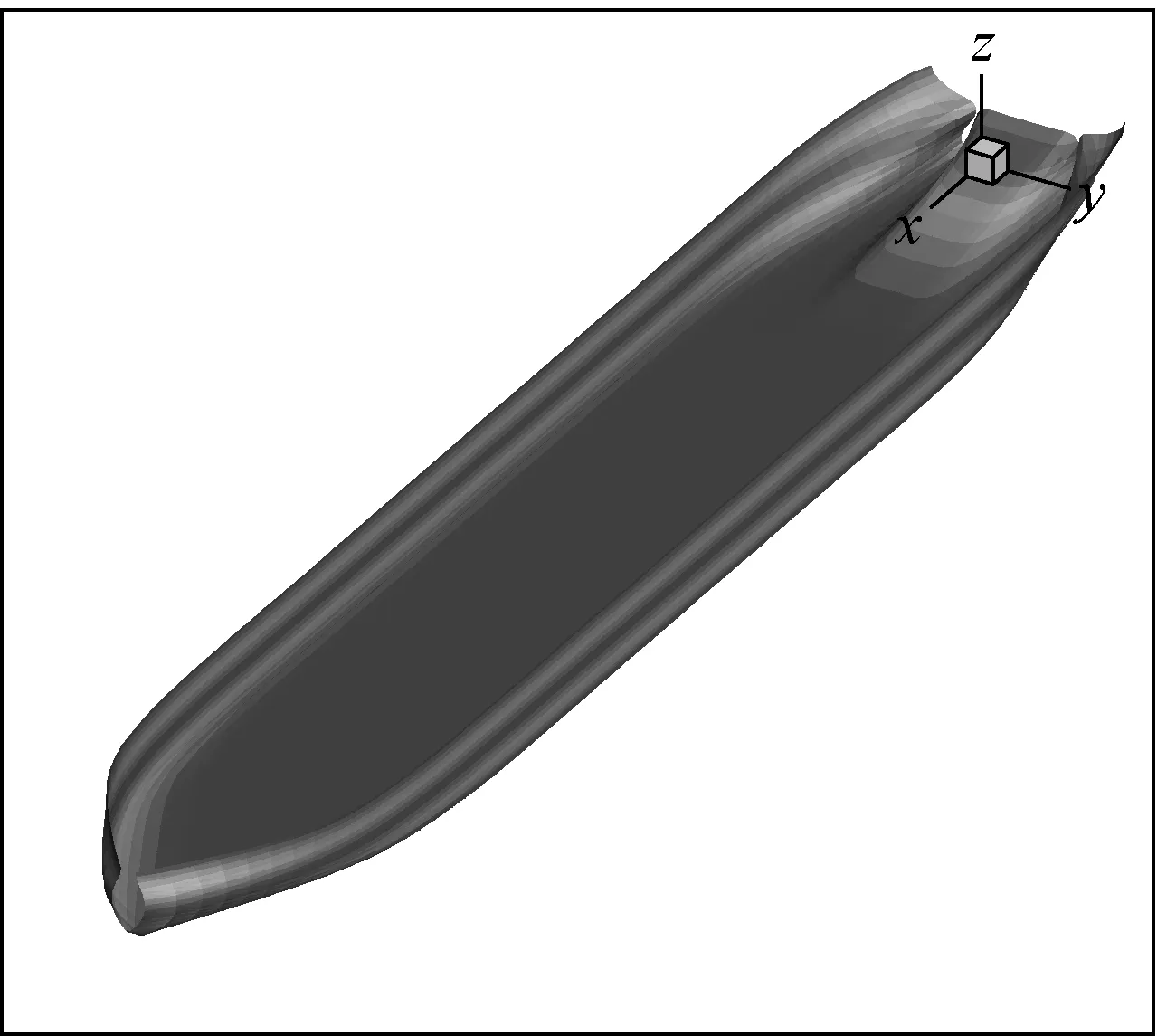
a) 平均湿表面

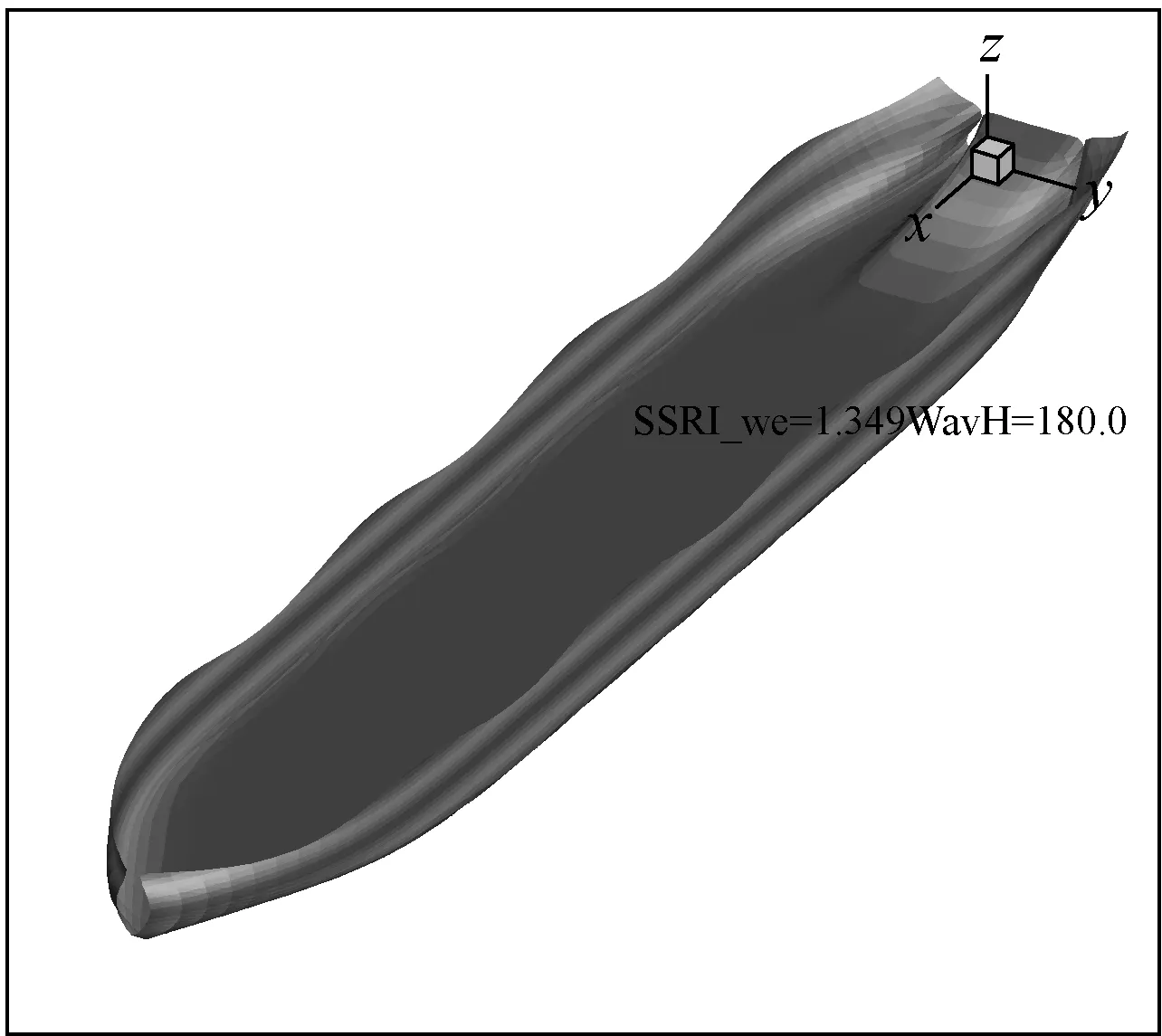
b) 某时刻瞬时湿表面

图2 考虑简单瞬时湿表面时波浪增阻修正方法计算流程图

1.2 简单湿表面处理

建立平动系O-xyz和物体系O-xbybzb，其中：平动系以船舶航速水平移动，z轴通过重心垂直向上，x轴指向船首，右手坐标系，y轴指向左舷；物体系固定在船体上，船体静水时物体系与平动系重合(见图3)。

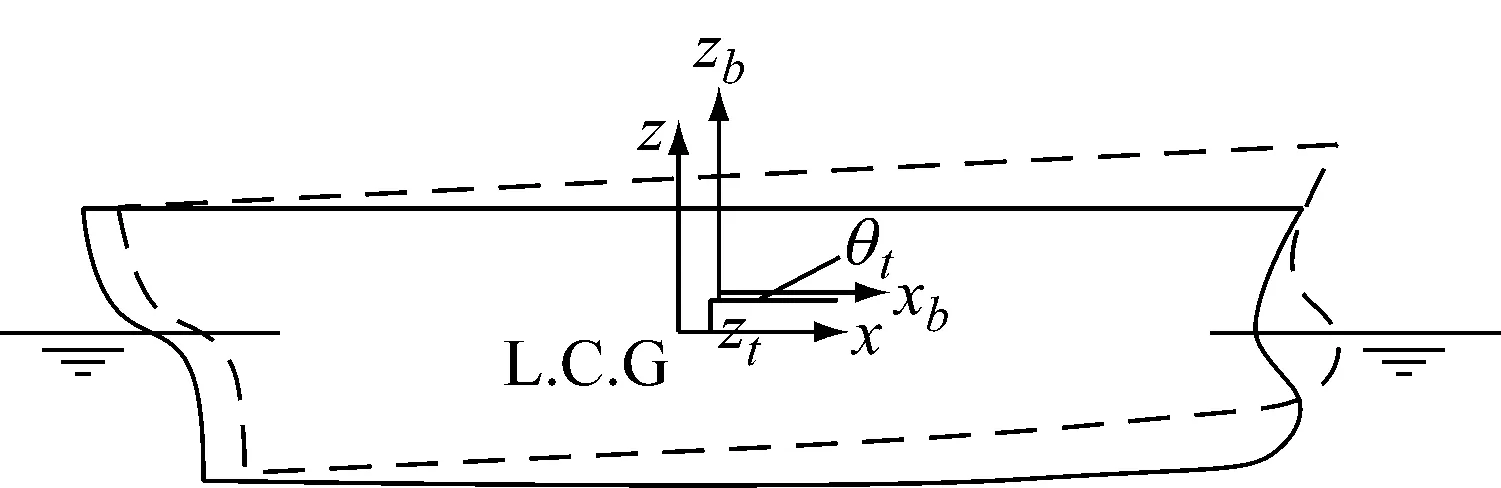
图3 坐标系统(平动系与物体系)

入射波为

ζt=ζacos(kxcosβ+kysinβ-kx)

(1)

则一个周期内某个时刻x处横剖面上波浪升沉可表示为

(2)

仅考虑船舶升沉纵摇运动对湿表面的影响，一个周期内某时刻x处横剖面的垂向变化为

(3)

式(3)中：Za和εz为升沉幅值及相位；θa和εθ为纵摇幅值及相位。

由此，瞬时湿表面上缘位置可由横剖面型值点(Yb,Zb)、横剖面的垂向变化ZH及波浪瞬时高度ζtj来确定(见图4)。同一时刻，分别对全船各横剖面进行计算获得船体与波浪瞬时交点位置，可得到整船的瞬时湿表面(如图1b所示)。

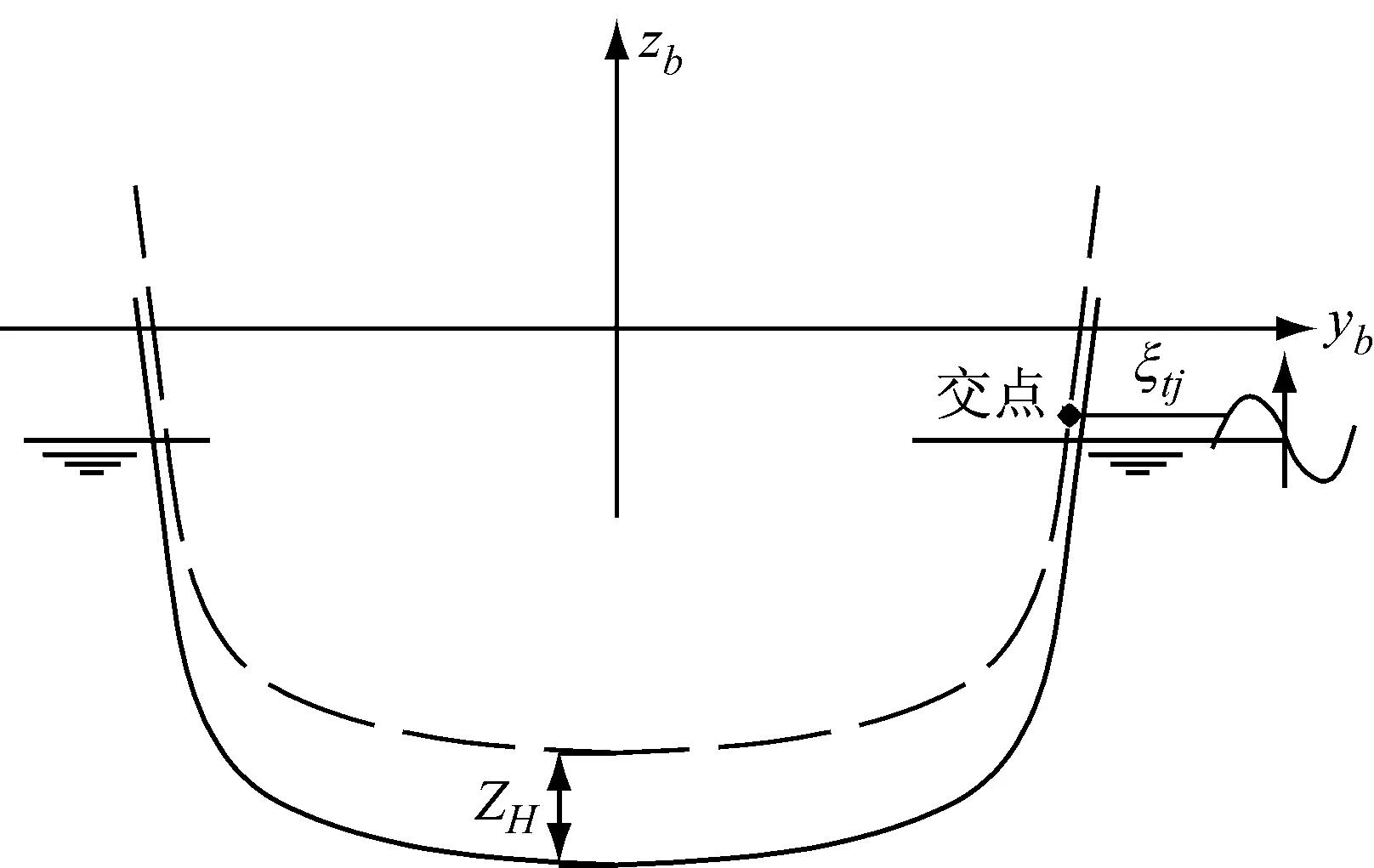
图4 船体与波浪瞬时交点位置

横截面上的FK力定义为

(4)

对整个船体上的FK力沿着船长进行积分得

(5)

(6)

式(5)和式(6)中：ρ为水密度；g为重力加速度；N3为截面中沿zb轴单位内法线的方向余弦；k为波数；β为浪向角(迎浪为180°)；ζa为波幅。

将一个周期分为NT个时刻，在每个时刻的瞬时湿表面上进行积分到FK1，最后取NT个平均值。

2 计算结果

将按照上述计算方法所得数值计算结果与试验结果进行对比，对比无因次波浪增阻系数为

(7)

式(7)中：RAW为规则波中波增阻；ρ为水密度；g为重力加速度；B为船模宽度；LPP为船模垂线间长；ζa为实际测得波高。

试验在上海船舶运输科学研究所拖曳水池中进行，水池尺寸为192 m(长)×10 m(宽)×4.5 m(水深)，耐波性试验所用造波机为电液伺服摇板式造波机，最大波高为0.3 m，频率范围为0.25～2.0 Hz。

图5中给出试验值、平均湿表面下的计算值及瞬时湿表面下的计算值的对比。从图5中可看出，考虑瞬

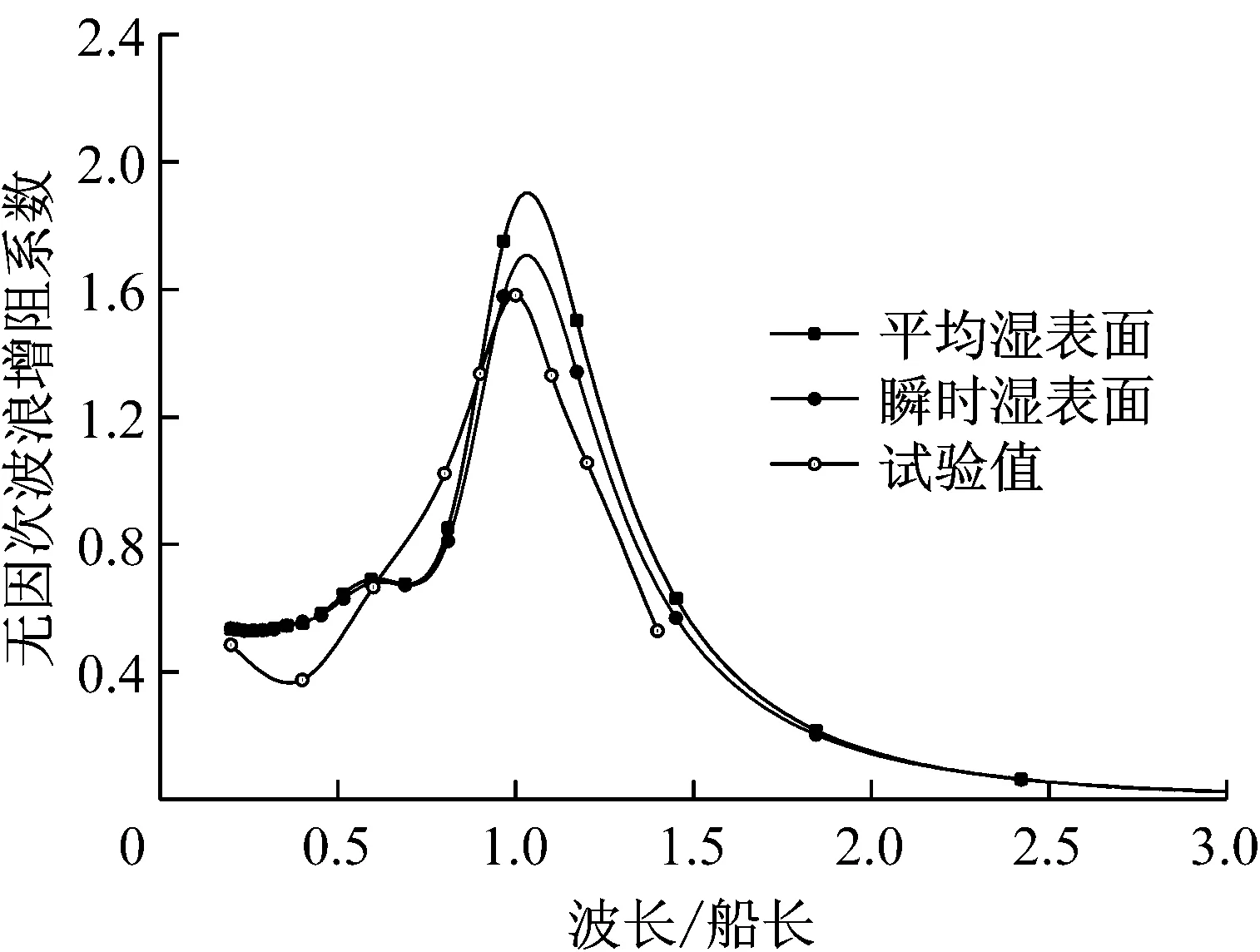
a) 航速Vs=10.5 kn, 迎浪

b) 航速Vs=12.0 kn, 迎浪

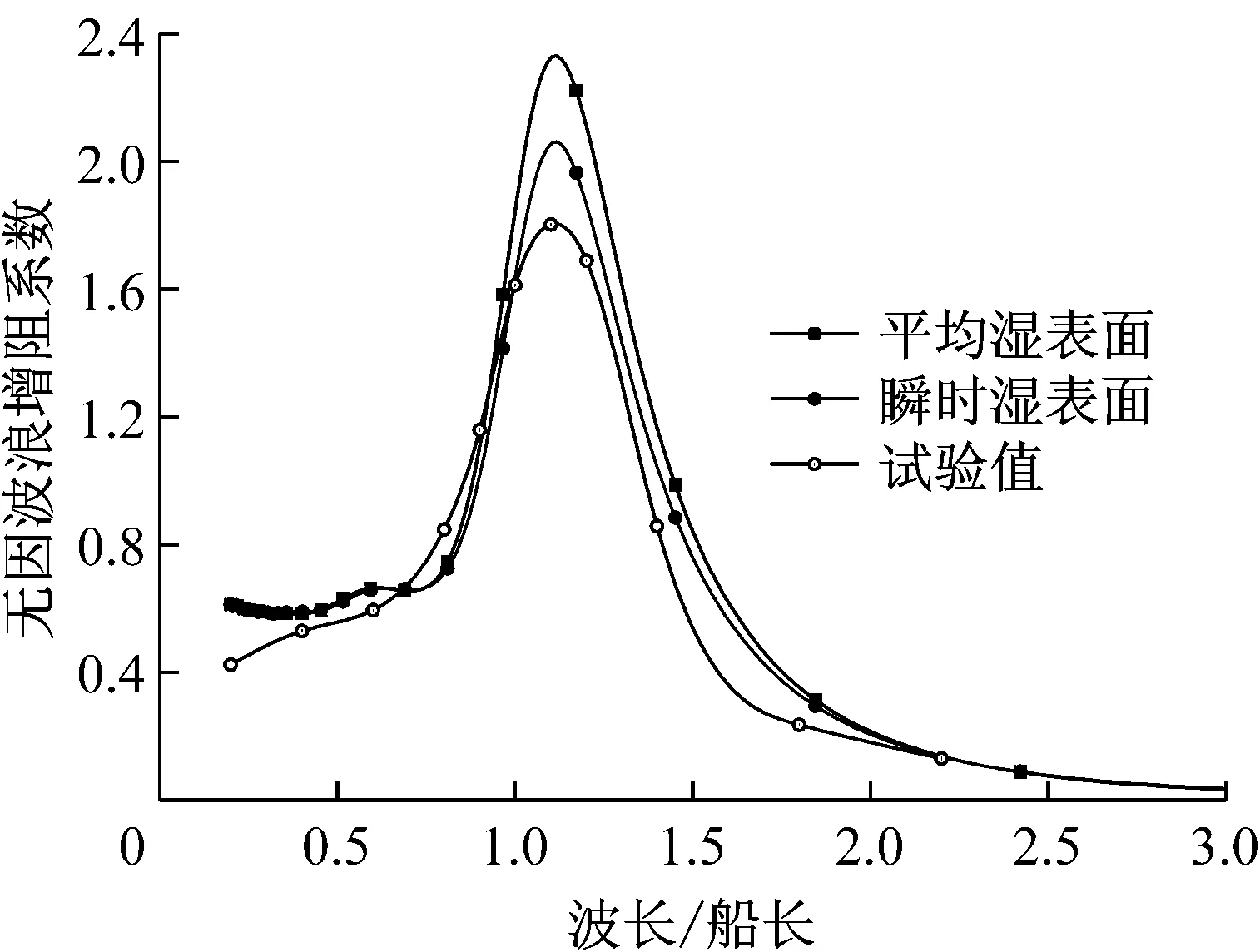
c) 航速Vs=13.5 kn, 迎浪

时湿表面时，波浪增阻与试验值较为接近，特别是峰值处计算值与试验值更为接近。表1中给出不规则波中瞬时湿表面及平均湿表面计算结果与试验结果差异。

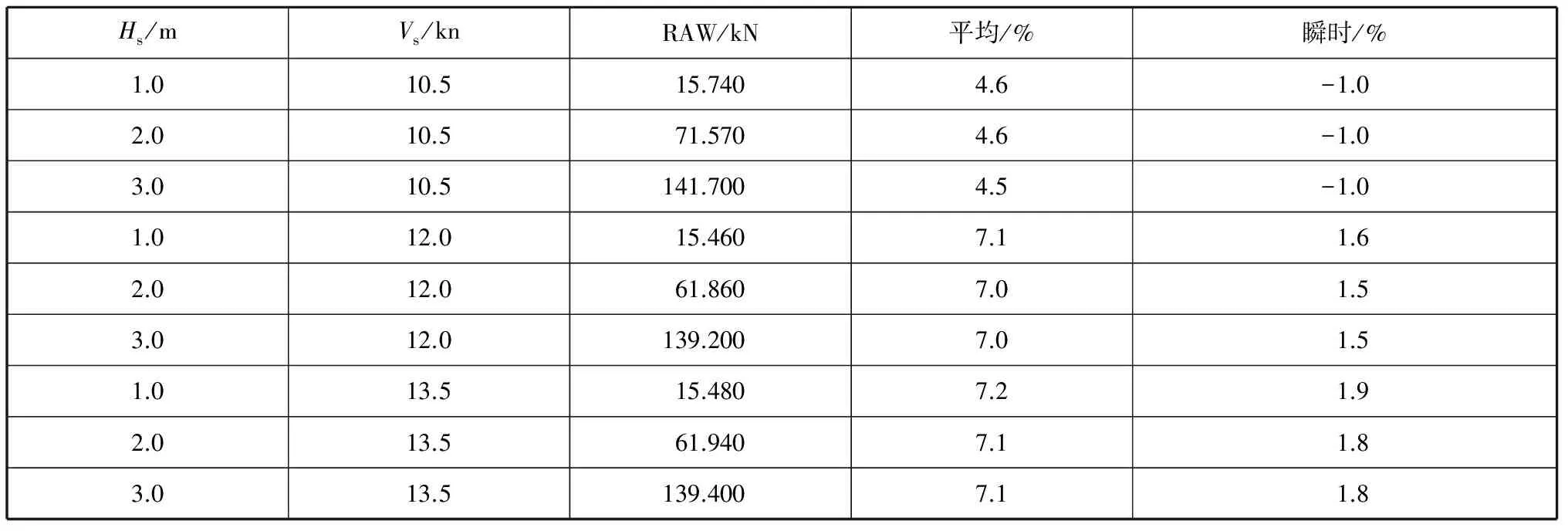
表1 不规则波中瞬时湿表面及平均湿表面计算结果与试验结果差异

3 结 语

在瞬时湿表面下计算平均FK力，得到修正的船舶运动，进而计算波浪增阻，并与平均湿表面情况下的计算结果及试验结果进行对比发现，考虑瞬时湿表面时波浪增阻预报精度有所提高。

[1] SALVESEN N, TUCK E O, FALTINSEN O. Ship Motions and Sea Loads[C]. SNAME, 1970(6):1-30.

[2] 陈京普，朱德祥. 船舶在波浪中运动的非线性时域数值模拟[J].水动力学研究与进展(A辑)，2010，25(6):830-836.

[3] 秦洪德.船舶运动与波浪载荷计算的非线性方法研究[D].哈尔滨:哈尔滨工程大学，2003.

[4] 李传庆. EEDI背景下船舶波浪增阻研究[D].哈尔滨:哈尔滨工程大学，2013.

[5] DUAN W Y, LI C Q. Estimation of Added Resistance for large Blunt Ship in Waves[J]. Journal of Marine Science and Application, 2013, 12(1):1-12.

[6] 李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社，2007.

Correction for the Instantaneous Wetted Hull in Calculating Wave Caused Added Resistance

LIChuanqing,GAOYuling,DONGGuoxiang
(State Key Laboratory of Navigation and Safety Technology,Shanghai Ship & Shipping Research Institute, Shanghai 200135, China)

When both incident waves and ship motion are harmonic, the mean Froude-Krylo(FK) forces obtained on instantaneous wetted hull and that obtained on the mean wetted hull are different due to nonlinear ship hull. This paper presents calculation results of FK forces on instantaneous wetted hull with STF method. And then added resistances due to waves are calculated after ship motion modified. The calculation results given instantaneous wetted hull and mean wetted hull compared with the experimental results. The comparison shows that the accuracy of added resistance calculation is improved by considering the Instantaneous Wetted Hull.

instantaneous wetted hull； Froude-Krylo force； STF method； added resistance

2016-07-26

国家科技支撑计划项目(2014BAG04B01)

李传庆(1987—)，男，安徽宿州人，助理研究员，硕士，主要从事波浪中船舶运动、波浪增阻数值预报及模型试验研究。

1674-5949(2016)04-0001-03

U661.1

A