炸药在空气中爆炸冲击波的地面反射超压实验研究

段晓瑜， 崔庆忠， 郭学永， 焦清介

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

炸药在空气中爆炸冲击波的地面反射超压实验研究

段晓瑜， 崔庆忠， 郭学永， 焦清介

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

为进一步研究炸药在空气中爆炸的冲击波参数，对梯恩梯(TNT)、HL0(黑索今(RDX)95%+石蜡(Wax)5%)和HL15(RDX 80%+Wax 5%+Al 15%)3种炸药不同距离处的冲击波反射超压进行了测试。实验结果表明：相比HL0和TNT，HL15在距爆炸中心3 m、4 m和5 m处的峰值超压最大；随着距离的增加，在7 m、9 m和12 m处，3种炸药的冲击波峰值超压越来越接近。采用幂指数公式对3种炸药的冲击波超压与对比距离之间的关系进行拟合后发现：在距离R≤2.6 m时，3种炸药的峰值超压大小顺序为HL0≥HL15>TNT；当2.6 m HL0 >TNT；对于指前因子k值，HL0>HL15>TNT；对于衰减系数α值，HL0>TNT>HL15；k值和α值共同决定着冲击波反射超压大小；幂指数拟合公式在取对数后为线性关系，在外推时得到的数据更接近实验值，因此可以作为研究炸药在空气中爆炸的地面反射超压经验公式。

兵器科学与技术； 空中爆炸； 冲击波反射超压； 相似关系； 幂指数拟合

0 引言

高能炸药设计是弹药威力设计的核心，提高战斗部的爆破能力主要是通过装填高能炸药来实现。炸药在空气中爆炸冲击波参数是评价战斗部毁伤威力的一个重要参数。通常认为爆炸冲击波参数是对比距离的函数[1]。Brode[2]用有限差分法计算了无限大理想气体中梯恩梯(TNT)的爆炸冲击波超压,并拟合成对比距离的多项式形式表达式；Henrych[3]根据TNT在自由场空气中爆炸冲击波峰值超压实验测试结果，也拟合出多项式形式的表达式；周南等[4]理论上推导了冲击波参数的普适公式，计算了1 000 t和1 000 kg TNT的爆炸参数，并与相应条件下的数值解和拟合公式进行了比较；童晓[5]研究了地面反射超压的测试及其影响因素，并测试了8 kg级TNT空中爆炸地面冲击波参数；仲倩等[6]提出了描述TNT冲击波超压峰值与比例距离关系的改进经验公式。以上均为对TNT冲击波超压的相关研究，冯晓军等[7]对1 kg 5种梯铝炸药的冲击波参数进行了研究，并分别拟合成多项式形式经验公式，但当量较小。

在冲击波参数的实际测试中，由于爆炸的破坏作用等原因，要测定大当量的自由场超压很困难，测试反射超压比直接测试自由场超压更容易实现；通常情况下冲击波反射参数代表着结构的爆炸载荷的上限[8]，如果能得到反射超压,对毁伤评估也是非常有参考价值的。由于存在马赫反射导致反射超压难于准确估算[9]。尽管地表反射超压经验公式已经存在并得到应用[10]，然而其计算较为繁琐，存在一些多次引用不准确的现象。含铝炸药作为一种典型的非理想炸药，现有地面反射超压公式的适用性尚未得到证明。本文拟探讨一种新的幂指数形式的经验公式。

为此，本文对TNT、HL0(黑索今(RDX)95%+石蜡(Wax)5%)和HL15(RDX 80%+Wax 5%+Al 15%)3种炸药的裸药柱在同一实验条件下的不同距离处的冲击波反射超压进行了测量，依据实验结果对3种炸药的超压公式进行了拟合，对照文献[12]结果对含铝炸药超压拟合公式的适用性进行了分析，同时对3种炸药冲击波参数的传输衰减特性进行了研究。

1 实验条件

1.1 实验炸药

由于含铝炸药是一种典型的非理想炸药，其非理想特性受装药量的影响较大，只有大当量装药的测试才能较为准确地描述其非理想特性。因此本实验采用的炸药装药量为10 kg/发，药柱长径比为2∶1.

1.2 测试条件

根据文献[7]，只有在满足对比炸高(爆炸高度/装药质量1/3)大于0.35 m/kg1/3时才可以忽略界面反射的影响，本实验选择炸高为1 m，可以忽略界面反射的影响。

测试场地选在开阔平坦的硬质土壤。在以爆炸中心为圆心的两条夹角为60°的圆半径上布置左路、右路两路空气壁面传感器，传感器距爆炸中心水平距离R分别为3 m、4 m、5 m、7 m、9 m和12 m. 传感器固定在直径300 mm 的钢制基座上，并保证传感器作用敏感面与地面平齐，以准确测试反射超压。传感器布置如图1所示。

图1 场地布置示意图Fig.1 Schematic diagram of site layout

1.3 测试仪器

采用量程为50 lb/in2、100 lb/in2及200 lb/in2的Kistler211B型压电压力传感器，传感器的谐振频率为300 kHz，灵敏度为50～100 mV/(lb·in-2)，记录仪采用了VXI-12047B高速数据采集仪。采样频率为10 MHz，记录时间为800 ms.

2 实验结果及数据处理

为保证数据的有效性，对波形与典型爆炸空气冲击波相差较远的数据予以剔除。图2为TNT爆炸距爆炸中心4 m处的超压曲线，波形虽然出现了干扰，但由于干扰位于第一个波峰之后，对于读取超压和冲量影响不大，故可以正常读数。同时对其他有类似波形和扰动的曲线依然采取这种方式鉴别和读数。

图2 TNT在空气中爆炸距爆炸中心4 m处的超压与时间曲线Fig.2 Pressure-time curve of TNT explosion at 4 m from the center of explosion

图3为实测TNT爆炸距爆炸中心3 m处的左路、右路超压时间曲线，两路测得反射超压曲线重复性好，其余实验距离处也可以观测到类似的几乎重叠曲线。

图3 TNT在空气中爆炸实验测试左路与右路的超压与时间曲线Fig.3 Pressure-time curves of TNT explosion at left and right locations

由于在测量自由场入射超压的过程中很难准确估计其三波点的高度，测试结果中难以区分入射波或马赫波，要想得到入射波只能通过提高自由场传感器的安装位置来实现[11-13]，同时由于实际毁伤目标时大多为反射超压的作用，测量其入射超压与实际应用不符，因此本文认为测量地面反射超压更具有比较性和实用意义，由于其测试重复性好，可以成为威力评估的一个重要方式。

图4为TNT爆炸后在不同距离处实测反射超压曲线，爆炸冲击波在传播过程中，冲击波的波形将不断发生变化，体现为压力和正压区冲量不断降低，正压作用时间不断加长。理想炸药爆炸形成的冲击波可以看作是简单的衰减演化过程。

图4 TNT在空气中爆炸在不同距离处实测的反射超压与时间曲线Fig.4 Reflected pressure-time curves of TNT explosion at different distances

对于含铝炸药，铝粉与爆轰产物发生反应放出能量，通常认为这部分能量不能用来支持爆轰波的传播，但会延缓冲击波过后介质压力的衰减，所以含铝炸药的冲击波在传输过程中不再是一个简单的衰减演化过程，而是一个释放能量和衰减的综合过程。

目前国内许多学者以及相关军用标准多采用最小二乘法拟合超压与距离的定量公式，这类公式一般在特定的范围内适用，但由于含铝炸药有着明显的尺寸效应，准确预测爆炸场内的冲击波参数需对各种量级的炸药进行精确测量，再拟合相关公式，具有相当大的难度。因此，有必要研究一种在更大范围内有效的拟合方式和公式来描述爆炸场的冲击波反射超压。

3 实验结果分析

3.1 冲击波超压实测值

图5为3种炸药在距爆炸中心5 m处的实测电压波形。

图5 3种炸药在距爆炸中心5 m处的实测电压波形Fig.5 Voltage curves of the three explosives at 5 m

TNT、HL0和HL15在不同距离处的冲击波峰值超压的实测平均值如表1所示，HL15在不同距离的超压测试值与平均值如图6所示，图7为3种炸药在不同距离处的平均峰值超压。

由表1可知，3种炸药在7 m、9 m和12 m处的冲击波超压的多次实验数据更为接近，这主要是由于在7 m、9 m和12 m处，测点与爆炸中心相距较远，震动对测试的干扰弱，测试系统的响应速度能准确捕捉到冲击波超压[14]。

HL15在3 m、4 m和5 m距离处4次测试超压值跳动很大(见图6)，多是由于测试技术和测试系统误差所引起。对于冲击波参数的测试，虽然一次实验的结果可能不太符合相似律，但多次实验值取平均值，依然可以表达为相似律关系，并推导出其公式。

根据图7可知，相比HL0和TNT，HL15在3 m、4 m和5 m处的峰值超压最大，随着距离的增加，在7 m、9 m和12 m处，3种炸药的冲击波峰值超压越来越接近。

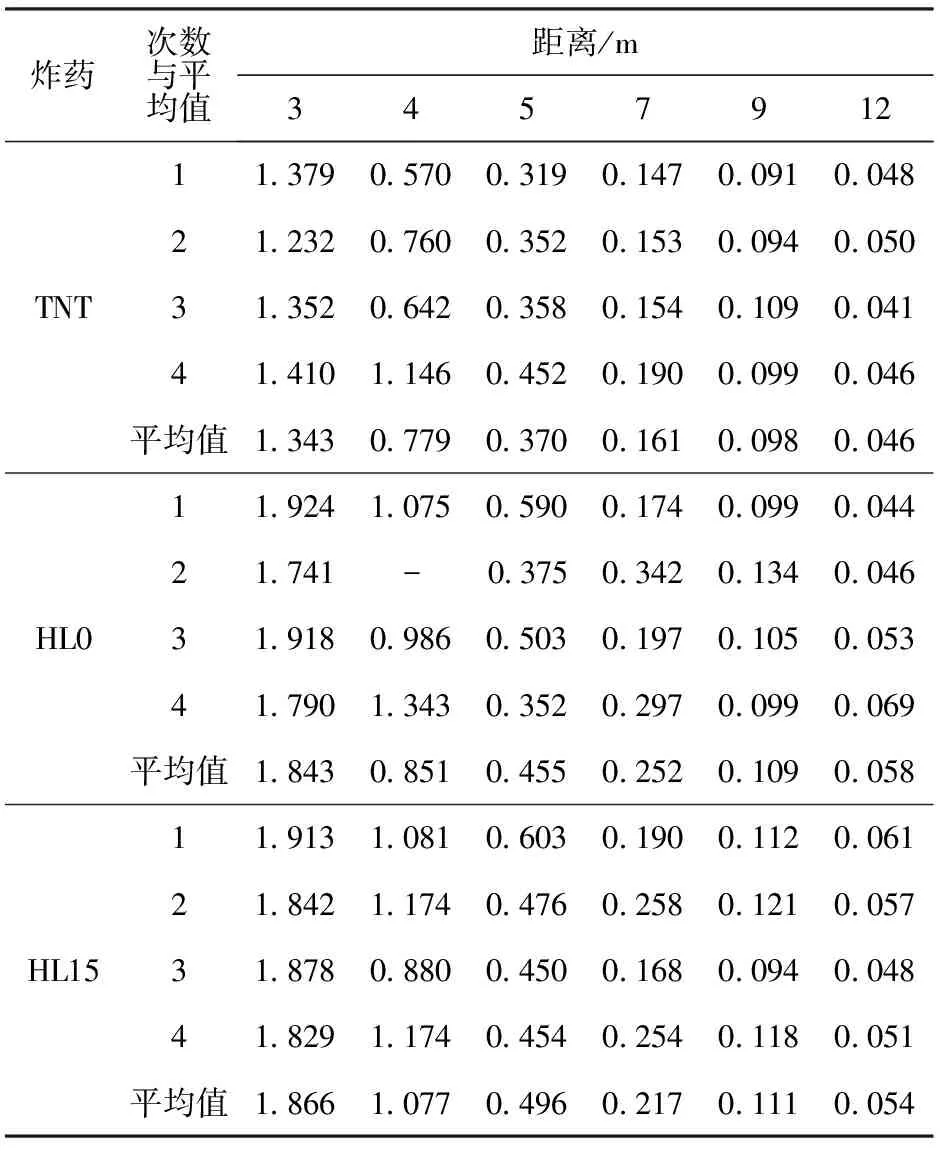
表1 3种炸药不同距离处超压测试值与平均值Tab.1 Test and average overpressures of the three explosives at different locations V

图6 HL15在空气中爆炸在不同距离处的超压测试值与平均值Fig.6 Average and test overpressure values of HL15

图7 3种炸药在空气中爆炸在不同距离处的峰值超压平均值Fig.7 Average overpressure values of the three explosives

3.2 冲击波超压的相似关系

(1)

式中：各待定系数a0,a1, …,an等，需要通过大量的实验数据加以处理才能得到[15]。常用计算TNT在空气中爆炸的冲击波峰值超压公式有Henrych和Brode公式，通常计算其他炸药的爆炸冲击波参数时，利用其TNT当量值进行估算。

通常水中爆炸冲击波参数的相似律公式表达为幂指数形式。国内外也有一些学者对一些炸药在空气中爆炸的冲击波超压采取幂指数拟合，但其多是针对理想炸药，而且多为小药量实验[16-19]。由于幂指数形式只有两个拟合参数，以及取对数后的关系式为线性关系式，利于外推和计算。本文分别对本次实验值和文献[12]中超压测试值进行了幂指数形式拟合：

(2)

式中：k为指前因子；α为衰减系数。

图8～图10列出了不同炸药在空气中爆炸的冲击波峰值超压实验测试结果，同时，将不同距离处的测试结果平均值按照幂指数形式拟合成了对比距离的函数关系，并标定了拟合相关系数。

图8 TNT冲击波峰值超压随距离变化Fig.8 Overpressure vs. distance of TNT

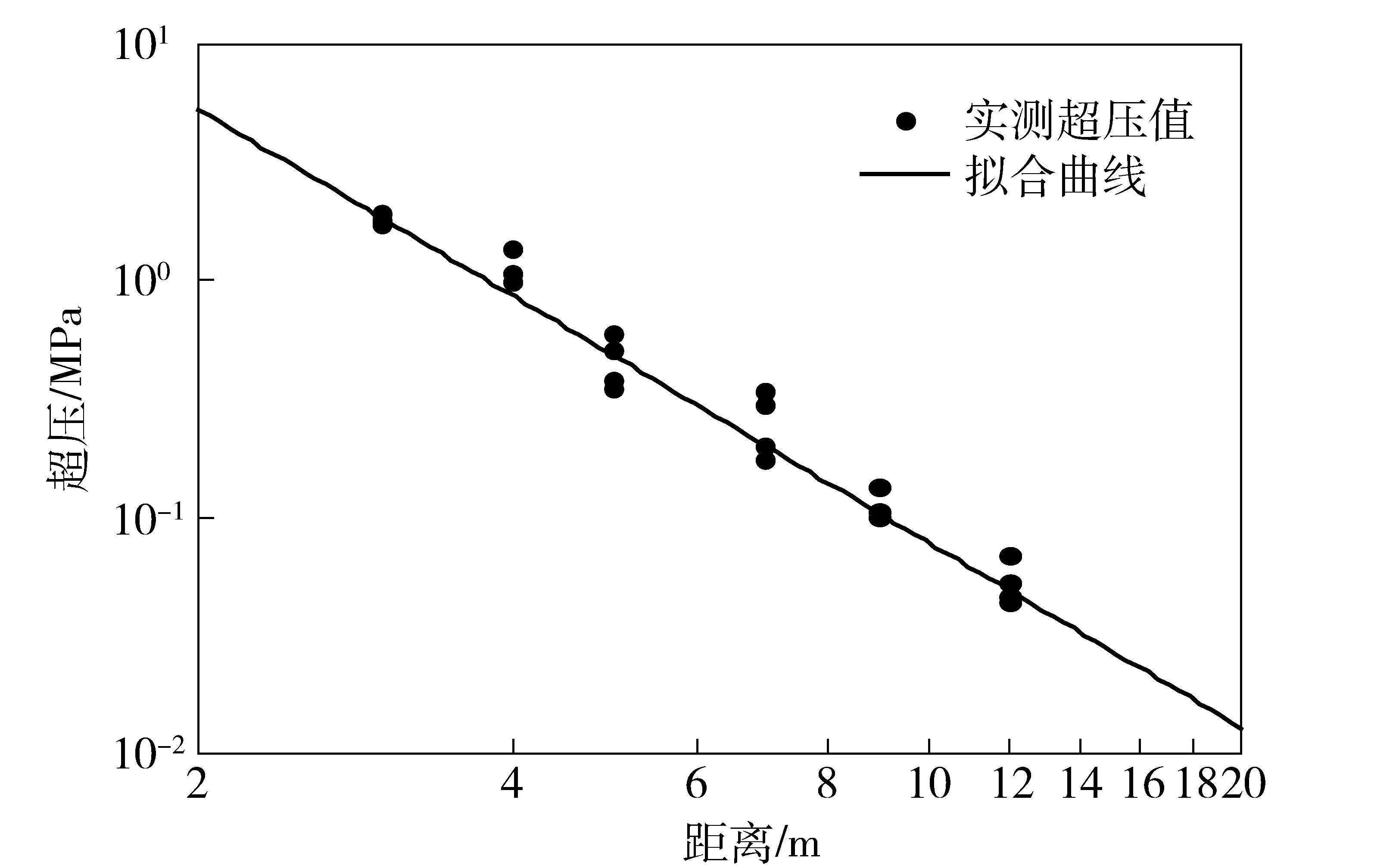
图9 HL0炸药冲击波峰值超压随距离变化Fig.9 Overpressure vs. distance of HL0

图10 HL15炸药冲击波峰值超压随距离变化Fig.10 Overpressure vs. distance of HL15

TNT冲击波超压拟合公式：

HL0冲击波超压拟合公式：

HL15冲击波超压拟合公式：

此外，在本文所选的6个测点中，若省去3 m处的超压值后，依据4 m、5 m、7 m、9 m、12 m处的实测超压拟合成多项式公式和幂指数公式，再分别计算3 m处的超压，拟合公式计算值和实验值对比如表2所示。

根据表2可知，在依据实验部分结果拟合成的多项式形式公式和幂指数形式公式时，可能由于测试系统不够稳定以及测试数据不够充分，导致二者计算误差较大，尽管这样，也还是幂指数拟合形式计算值相对误差更小，对于3种炸药其相对误差均小于10%. 通过对文献[5]和文献[7]给出的实验结果进行拟合以及计算，也可以得出如上结论。

表2 除3 m外测点的超压拟合公式及其对3 m处超压的计算值与实测值Tab.2 Calculated and test overpressure values

以往人们依据实验结果拟合的经验公式，一般只在原测试范围内有效，这就导致了对近爆炸中心处的冲击波压力场分布的经验公式计算值与数值模拟结果[20]、实验结果[1]差异较大，而幂指数形式拟合公式的计算值与实测值差异相对较小。

图11为拟合得到的3种炸药的地面反射超压距离曲线。由图11可知，HL0和HL15炸药的峰值超压值均大于TNT炸药。其中：当R≤2.6 m时，3种炸药的峰值超压HL0≥HL15>TNT；当2.6 mHL0>TNT.

图11 3种炸药的峰值超压与距离曲线Fig.11 Overpressure-distance curves of three explosives

在能量输出演化过程中，铝粉的加入导致HL15的初始冲击波强度比HL0小，表现为指前因子k的大小。在近场处(R≤2.6 m)的冲击波超压值小于HL0，随着铝粉燃烧对冲击波的支持作用，使得HL15的衰减系数更小，而HL0的衰减系数是三者之间最大，导致了HL0的峰值超压衰减较快，在2.6 m

4 结论

1)测量炸药在空气中爆炸的冲击波超压时，采用测量反射超压的办法更为简便，测试重复性好，可以用来比较炸药威力；单次实验与相似律关系符合差，但通过对多次实验取平均值后依然可以表达为相似律关系。

2)由于幂指数形式的拟合公式取对数后为线性表达式，冲击波超压的相似关系采用幂指数公式更为合适，尤其是测试点较少时更为准确。

3)依据幂指数公式拟合的超压时间曲线可以看出：当R≤2.6 m时，3种炸药的峰值超压HL0≥HL15>TNT；当2.6 mHL0>TNT.

4)在对3种炸药冲击波超压相似关系进行幂指数拟合后，对于指前因子k值，HL0>HL15>TNT；对于衰减系数α值，HL0>TNT>HL15；k值和α值共同决定冲击波反射超压的大小。

References)

[1] Swisdak M M. Explosion effects and properties: part I-explosion effects in air, A018544[R]. New York: Naval Surface Weapons Center, 1975:10-16.

[2] Brode H L. Numerical solutions of spherical blast wave[J]. Journal of Applied Physics, 1955, 26(6):766-775.

[3] Henrych J. The dynamics of explosion and its use[M]. Amsterdam, NL: Elsevier, 1979:204-207.

[4] 周南, 田宙. 爆炸冲击波参数计算的普适公式[J]. 兵工学报, 1995, 16(3):23-27. ZHOU Nan, TIAN Zhou. A universal formula for the prediction of air-shock wave parameters during explosion[J]. Acta Armamentarii, 1995, 16(3):23-27. (in Chinese)

[5] 童晓. 爆炸场冲击波压力测量及数据处理方法研究[D].南京:南京理工大学, 2015:74-80. TONG Xiao. The research of the measurements of shock wave and the method of data treatments[D]. Nanjing: Nanjing University of Science and Technology, 2015:74-80. (in Chinese)

[6] 仲倩, 王伯良, 黄菊, 等. TNT空中爆炸超压的相似律[J]. 火炸药学报, 2010, 33(4):32-35. ZHONG Qing, WANG Bo-liang, HUANG Ju, et al. Study on the similarity law of TNT explosion overpressure in air[J]. Chinese Journal of Explosives & Propellants, 2010, 33(4): 32-35.(in Chinese)

[7] 冯晓军, 王晓峰, 黄亚峰, 等. 铝粉含量对梯铝炸药爆压和冲击波参数的影响[J]. 火炸药学报, 2009, 32(5): 1-4. FENG Xiao-jun, WANG Xiao-feng, HUANG Ya-feng, et al. Effect of aluminium content on the detonation pressure and shock wave parameters of TNT/Al explosives[J]. Chinese Journal of Explosives & Propellants, 2009, 32(5):1-4 (in Chinese)

[8] Baker W E. Explosions in air[M]. Austin, TX, US: University of Texas Press, 1973.

[9] 北京工业学院八系. 爆炸及其作用：下册[M]. 北京:国防工业出版社, 1979:15-25. The Eighth Department of Beijing Institute of Technology. Explosions and effects: Volume II[M]. Beijing:National Defense Industry Press, 1979:15-25. (in Chinese)

[10] 孙业斌. 军用混合炸药[M]. 北京:国防工业出版社, 1969:364-369. SUN Ya-bin. Military mixing explosives[M]. Beijing: National Defense Industry Press,1969:364-369.(in Chinese)

[11] 郭炜, 俞统昌, 金朋刚. 三波点的测量与实验技术研究[J]. 火炸药学报, 2007, 30(4):55-61. GUO Wei, YU Tong-chang, JIN Peng-gang. Test of triple point and study on its test technology[J]. Chinese Journal of Explosives & Propellants, 2007, 30(4):55-61.(in Chinese)

[12] 王建灵, 郭炜, 冯晓军. TNT_PBX和Hexel空中爆炸冲击波参数的实验研究[J]. 火炸药学报, 2008, 31(6):42-44,68. WANG Ji-ling, GUO Wei, FENG Xiao-jun. Experimental research on the a ir explosion shock wave parameters of TNT, PBX and Hexel[J]. Chinese Journal of Explosives & Propellants, 2008, 31(6):42-44,68. (in Chinese)

[13] 赵赫. 温压炸药爆炸毁伤效能评估实验研究[D]. 北京：北京理工大学, 2008:36-40. ZHAO He. Experimental study of the damage effectiveness evaluation of thermobaric explosive[D]. Beijing:Beijing Institute of Technology, 2008:36-40.(in Chinese)

[14] 黄正平. 爆炸与冲击电测技术[M]. 北京:国防工业出版社, 2006:38-52. HUANG Zheng-ping. Explosion and shock measuring technology[M]. Beijing: National Defense Industry Press, 2006:38-52. (in chinese)

[15] 谭庆明. 量纲分析[M]. 合肥:中国科学技术大学出版社, 2005:99-102. TAN Qing-m. Dimensional analysis[M]. Hefei: University of Science and Technology of China Press, 2005:99-102. (in chinese)

[16] Zhou Z Q, Nie J X, Ou Z C, et al. Effects of the aluminum content on the shock wave pressure and the acceleration ability of RDX-based aluminized explosives[J]. Journal of Applied Physics, 2014, 116(14):144901-144907.

[17] Gran J K, Ehrgott J J Q, Cargile J D, et al. Cavity expansion experiments with spherical explosive charges in concrete, ERDC/GSL-SR-09-4[R]. Vicksburg MS:Engineer Research and Development Center, Geotechnical and Structures Lab, 2009:1-38.

[18] Vadhe P P, Pawar R B, Sinha R K, et al. Cast aluminized explosives (review)[J]. Combustion Explosion & Shock Waves, 2008, 44(4):461-475.

[19] Fowles R, Williams R F. Plane stress wave propagation in solids[J]. Journal of Applied Physics, 1970, 41(1):360-363.

[20] 辛春亮, 徐更光, 刘科种, 等. 考虑后燃烧效应的TNT空气中爆炸的数值模拟[J]. 含能材料, 2008, 16(2):160-163. XIN Chun-liang, XU Geng-guang, LIU Ke-zhong, et al. Numerical simulation of TNT explosion with post-detonation burning effect in air[J]. Chinese Journal of Energetic Materials, 2008, 16(2):160-163. (in Chinese)

Experimental Investigation of Ground Reflected Overpressure of Shock Wave in Air Blast

DUAN Xiao-yu, CUI Qing-zhong, GUO Xue-yong, JIAO Qing-jie

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

In order to investigate the parameters of shock wave in air blast, the ground reflected overpressures of TNT, HL0(RDX 95%+Wax 5%)and HL15(RDX 80%+Wax 5%+Al 15%) at different locations were tested. Test resultes show that the peak overpressures of HL15 are maximal at 3 m, 4 m and 5 m from the center of explosion compared with TNT and HL0. The peak overpressures of three explosives get closer to each other at 7 m, 9 m and 12 m from the center of explosion with the increase in distance. Power exponential formulas are used to fit the relationship between peak overpressure and scaled distance. The fitting results show that the magnitude order of peak overpressures is HL0≥HL15>TNT forR≤2.6 m; the magnitude order of peak overpressures is HL15> HL0 >TNT for 2.6 m

ordnance science and technology; air blast； reflected overpressure； similarity relationship； power exponential fitting

2016-01-20

国家国防科技工业局预先研究项目(00402010301)

段晓瑜(1990—), 女, 博士研究生。E-mail: dxy900401@163.com； 崔庆忠(1969—)，男，副研究员，硕士生导师。E-mail:cqz1969@bit.edu.cn

O384

A

1000-1093(2016)12-2277-07

10.3969/j.issn.1000-1093.2016.12.013