直线参数方程在高中数学中的应用
江苏省苏州高等幼儿专科学校 刘 艳
直线参数方程在高中数学中的应用
江苏省苏州高等幼儿专科学校 刘 艳
数学本是较难的科目,但其对于学生的综合分数起着重要作用。直线参数方程是数学知识体系中的重要组成部分,对于解析几何相关问题的求解有着重要的应用价值。然而,其对于学生而言,不仅在理解上有较大难度,在实际解题应用中也存在着巨大的困难。学生无法结合题目的主要条件进行有效分析,且在解题应用中缺乏灵活性,导致解题过程陷入僵局。本文重点从最值求解题、定值类数学题和轨迹问题三个方面入手,探讨直线参数方程在数学中的实际应用。
直线参数方程;数学;应用
随着新课改的不断深化,基于对高中文科学生学习能力和状况的研究,并为了有效平衡数学教材的教学内容,目前直线参数方程内容的比例已经有了显著减少,在实际教学当中教师也进行了教学重心的偏移。然而,作为数学体系的重要组成部分,其在实际解题应用当中,尤其是一些灵活性和深刻性要求较高的数学习题当中,能发挥极佳的应用优势。为了保证高中数学知识结构体系的完整性,提高其数学素养和解题能力,应当对直线参数方程在数学解题中的有效应用进行系统讲解和分析。
一、直线参数方程应用于最值求解题
高中几何图形中最值问题解析是重点和难点,尤其对学生来说,由于数学基础扎实程度不够,且在解题和答题中的灵活性不强,无法充分应用所学的数学知识进行辨证式解题,很容易陷入到解题过程当中。由于不能明确已知条件的实际映出,且无法抓住题目的重点,往往选择以自身所掌握的单一化解题方式进行剖析和解答,不仅耗时较长,且最终答案难以保证正确率。
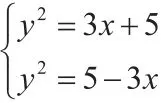
对本题的解题过程进行分析,应用直线参数方程进行解题,不仅解题过程思路清晰明确,且快速高效,以图形和已知条件作为推导元素,便能很快获得问题答案。由此总结出,学生应当有意识加强相关题目的解题训练,以有效掌握此种解题方法,提高解题过程的效率。
二、直线参数方程应用于定值类数学题
定值类数学题同样是高中数学中的重点和难点,学生在面对相应题目时往往找不到解题方向,缺乏具体的着眼点,导致数学学习自信心的逐渐弱化。对于此类题目的解题而言,单纯利用已知条件,即题目变量并不能明确点的横纵坐标亦或是由点构成的直线,且点属于未知元,直接进行解题很难找出一条快速有效的解题道路。而利用直线参数方程知识,将原有条件转化为一个参变元,则解题过程清晰和简单。
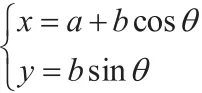
证明题是高中数学习题中的重要题型,对于学生逻辑思维能力和推导能力的训练和提升有着重要意义。教师在进行教学时,应当引导学生充分利用已知条件,首先完成参数方程设置,进而一步步推导出题目要求。
三、直线参数方程应用于轨迹问题
对于轨迹问题的解答,往往需要借助已知条件进行画图,在图形观察过程中找出解题的突破口,最后得到所需答案。文科生由于图形构建和理解能力上的欠缺,往往在面对轨迹问题时难以下手,这就要求教师在进行相应知识点的讲解时,一步步引导学生掌握高效的解题推导方法。
以圆曲线方程问题为例,题目通常给出圆的方程,并给出相关已知条件,让学生求出动点关于圆曲线的方程。此类问题有着很强的数形结合特色,需要学生在解题过程中充分结合几何图形知识和方程知识,利用直线参数方程求出关于圆曲线的方程。在解题过程中,学生应首先明确题目所给条件,并将已知条件进行有效整理,以已知条件作为基础,设定出过原点直线的方程组。其后,以已知条件为基础画出相应图形,在数形的配合下,明确动点方程组,并实现动点方程组向已知量的转化。最后,以已知量作为补充,解答出轨迹问题的答案。
从数学出题结构来看,此类题型往往为数学考试卷后部的推导解答题,不仅解题过程相对复杂,且难度较大,需要花费一定时间。如学生没有扎实的数学基础,且无法充分应用直线参数方程作为解题参考,则解题过程漫长且艰难,浪费其大量的考试时间。因此,学生应在平时多进行相关习题的训练,以打牢基础为解题提供充足准备。若在考试当中应用直线参数方程进行解题仍无法解答,则应选择挪后或跳过,保证整体其他题目充足的答题时间。
总之,直线参数方程在高中数学知识体系中有重要地位,这就要求教师在日常教学当中,依据教学实际情况,将其与其他知识点进行串联讲解,使学生在学习过程中进行知识的融会贯通,确保其知识体系的完整性。学生应当充分重视对数学科目的学习,并着重于直线参数方程知识点的学习,将直线参数方程与其他知识点结合起来,并在解题过程中应用多种解题方案,着重应用直线参数方程完成最值求解题、定值类数学题和轨迹问题的求解。
[1]邱波.巧用直线的参数方程处理线段长度问题[J].数学通讯,2014(Z1):36-39.
[2]吴燕.直线的参数方程在解题中的应用[J].考试周刊,2014,11:51-52.
[3]周晓林.如何用直线的参数方程来优化解题[J].中学生数理化(学研版),2015(04):33-34.
[4]王爽.浅谈直线的参数方程[J].吉林教育,2011(26):62.

