等腰三角形中悟分类思想

江苏省海门市海南中学 龚 杰

等腰三角形中悟分类思想

江苏省海门市海南中学 龚 杰

分类思想是初中阶段的核心数学思想，也是中考的必考点。正确进行分类讨论的关键是弄清楚分类的依据。对于初二学生而言，代数的分类经历过绝对值的分类、方程无解的分类，几何上遇到的分类情况就更少了，遇到分类讨论比较多的就是等腰三角形这一特殊的三角形。等腰三角形中有很多涉及分类思想的题目，遇到这类题目，常犯的错误就是“漏解”，怎么才能避免这种情况的产生呢？如何从对等腰三角形的分类有进一步的理解后对分类思想有进一步的思考？本文从分类的依据入手，谈谈如何把握等腰三角形的分类点，从而正确做到“不重不漏”，避免“漏解”情况的发生。

三角形的基本构成元素就是边和角，还有三条重要的线段。下面我们就这几点来讨论一下等腰三角形的分类情况。

一、遇边要分为“腰”和“底”

例1 等腰三角形两条边的长度分别为7和8，则它的周长为_____ 。

分析：题目的已知条件中提到等腰三角形的两条边长，但是并没有指明边长7和8中，哪条长度是腰长，哪条长度是底边的长，所以我们就要分类。当等腰三角形的腰长是7时，这个等腰三角形的底边长就是8，则此时等腰三角形三条边的长度分别为7，7，8，它的周长就是7+7+8=22；当等腰三角形的腰长是8时，这个等腰三角形的底边长就是7，则此时等腰三角形三条边的长度分别为7，8，8，周长就是7+8+8=23。然后我们考虑一下三角形的三边关系，发现都可以。故这个等腰三角形的周长等于22或23。

例2 等腰三角形两条边长分别为4和8，则它的周长为_____ 。

分析：同例1一样，题目的已知条件中提到等腰三角形的两条边长，但是并没有指明边长7和8中，哪条长度是腰长，哪条长度是底边的长，所以我们仍然要分类。当等腰三角形的腰长是4时，这个等腰三角形的底边长就是8，则此时等腰三角形三条边的长度分别为4，4，8，它的周长就是4+4+8=16；当等腰三角形的腰长是8时，这个等腰三角形的底边长就是4，则此时等腰三角形三条边的长度分别为4，8，8，周长就是4+8+8=20。但是考虑到三边组成三角形要满足三角形的三边关系，因为4+4=8，所以这种情况不成立。故这个等腰三角形的周长等于20。

归纳：在等腰三角形的题目中，若条件中涉及到等腰三角形的边长，没有图又没有明确哪条是底边长，哪条是腰长时，应该在符合三角形三边关系的前提下分类讨论。

二、遇角要分为“顶”和“底”

例3 已知等腰三角形的一个内角的度数是70°，则它的三个内角的度数分别是_____。

分析：题目的已知条件中提到等腰三角形的一个内角的度数，但是并没有指明70°是顶角还是底角，所以我们就要分类。当等腰三角形的顶角是70°时，这个等腰三角形的底角度数就是（180°-70°）=55°，则此时等腰三角形的三个内角的度数分别为70°，55°，55°；当等腰三角形的底角是70°时，这个等腰三角形的顶角度数就是180°-2×70°=40°，则此时等腰三角形的三个内角的度数分别为70°，70°，40°。

例4 已知等腰三角形的一个内角是110°，则它的三个内角的度数分别是_______。

分析：同例3一样，题目的已知条件中提到等腰三角形的一个内角的度数，但是并没有指明110°是顶角还是底角，所以我们就要分类。当等腰三角形的顶角是110°时，这个等腰三角形的底角度数就是（180°-110°）=35°，则此时等腰三角形的三个内角的度数分别为110°，35°，35°；当等腰三角形的底角是110°时，这个等腰三角形的顶角度数就是180°-2×110°=-40°，而三角形的内角不可能是负数，所以这种情况舍去。

归纳：在等腰三角形的题目中，若条件中涉及到等腰三角形的角的度数，没有图又没有明确哪个角是顶角，哪个角是底角时，应该在符合三角形内角和是180°的前提下分类讨论。顶角的取值范围0°～180°，底角的取值范围0°～90°。

例5 平面直角坐标系中有点A（3，-3），在x轴上确定一点P，使△AOP是等腰三角形，这样的点P有______个。

分析：△AOP是等腰三角形，三角形中三个顶点A，O，P中点A，点O已确定，我们只要寻找点P即可。三角形的三条边中边AO已经确定，但是AO是腰还是底边还不知道，这就需要分类讨论了。

首先我们认为AO是腰，腰有两个端点，谁是顶点还不确定，所以我们需要再次分类。

（1）AO为腰，A为顶点，那就说明AO=AP，所以我们只要以A为圆心，AO长为半径，画圆，与x轴的交点有2个，一个与O重合，另一个就是我们要找的第一个P点；

（2）AO为腰，O为顶点，那就说明OA=OP，所以我们只要以O为圆心，OA长为半径，画圆，与x轴的交点有2个，两个都是我们要找的P点；这样我们就找到了3个P点。

其次就是AO是底，底有两个端点，都不是顶点，所以我们不需要分类。

（3）AO为底边，P就是顶点，那就说明PA=PO，所以我们需要找一个P点到AO两端点的距离相等，所以P在AO的垂直平分线上，我们画线段AO的垂直平分线与x轴有1个交点，这就是我们腰找的第4个点P。

综上所述，这样的P点一共有4个。

归纳：对于寻找等腰三角形可以按照逐步分类的方法来思考，这样就能不重不漏地找到了，而且不管题目如何变，在x轴上找，还是在y轴上找，用这个方法都能逐步解决。

三、遇高要分为“内”和“外”

例6 已知等腰三角形一腰上的高与另一腰的夹角为45°，则顶角的度数为_________ 。

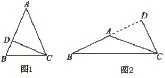
分析：三角形的高一般分为三种，锐角三角形的三条高都在形内，直角三角形的两高在边上，一条在形内，钝角三角形的两条高在形外，一条在形内。因为无图，所以不知道顶角是锐角，直角还是钝角，所以要分类讨论。高在边上不能形成夹角，所以直角舍去。我们可以画出图形进行解决问题。

由图1可知顶角为45°，由图2可知顶角为135°。

归纳：对于等腰三角形的中出现高，如果无图就要分类讨论，得出两个结论，而且这两个角是互补的。

通过以上对等腰三角形中分类思想的讨论，我们应该对于分类思想有了基本的认识，在今后的几何学习和代数学习中首先要弄清楚每一个知识点，才能在遇到分类情况时能够又快又准地找到分类依据，从而就能不重不漏地进行解答。