聚焦思维生成，构建灵动数学课堂

江苏省海门市第一中学 黄乃云

聚焦思维生成，构建灵动数学课堂

江苏省海门市第一中学 黄乃云

在新课改背景下，高中数学课堂教学中，教师应注意尊重学生的主体地位，聚焦学生思维生成，结合学生学情和学科特点，优选有效策略，引导学生善于观察，勤于思考，乐于探究，敢于质疑。本文对此进行了分析研究。

思维；生成；灵动；数学；课堂

思维是一切发明创造活动的重要基础。数学是思维的体操，然而在数学教学中，受传统教育思想的束缚，许多教师过于偏重知识传授和技能操练，忽略了学生思维的生成和培养，影响了学生思维品质的发展，导致课堂模式化，缺乏灵动性，教学效率低下。对此，笔者结合教学实践，就如何在高中数学教学中聚焦学生思维生成,构建灵动数学课堂提出了自己的几点建议，以期抛砖引玉。

一、展示概念背景，丰富表象，调动学生思维主动性

思维主动性是指学生在学习过程中能够积极主动思考，自主获取知识，体验成功的喜悦感。数学概念是构造数学知识的重要基础，是数学思维的主要依据。在以往数学概念教学中，许多教师往往倾向于将一连串的数学概念直接抛给学生，忽略了学生思维的主动性，学生机械被动地接受概念，导致学生概念理解不到位。每个数学概念的形成都蕴含着丰富的知识背景，在数学概念教学中，教师要注意展示概念背景，借助多媒体教学手段，揭示概念的产生过程，从而激发学生主动思维，帮助学生建立丰富的表象。

比如，学习“异面直线的夹角”时，在新课伊始阶段，笔者首先通过多媒体课件向学生展示熟悉的正方体模型，然后在此基础上引导学生对空间两条直线的位置关系进行回顾和总结，接着让学生仔细观察课件中出示的几对异面直线，并思考探究：“从位置关系上分析，同为异面直线，他们的相对位置是否存在不同？”学生异口同声地回答道：“肯定存在不同。”笔者继续追问：“既然存在不同，那么则意味着仅用‘异面’是难以全面描述出异面直线间的相对位置，怎样才能全面准确地刻画出异面直线间的相对位置呢？”这样的新课导入，给学生以直观感知，通过揭示“异面直线所成的角”这一数学概念的背景，让学生带着疑问去学习新知，自主探究新知，调动了学生思维积极性和主动性，点燃了学生思维之火。

二、创设探究活动，探索实践，培养学生思维创造性

《数学课程标准》提出：在教学过程中，教师应从学生已有知识经验出发，创设一定的教学活动，引导学生自主、合作、探究学习。探究活动是培养学生思维深刻性和创造性的重要途径。在高中数学教学中，教师应结合学生学情和认知实际，以教材知识点为依托，精心设计富有开放性、探究性以及挑战性的学习活动，引导学生主动参与、积极思维、实践探究、合作交流，从而培养学生创造性思维，提升学生实践探究、自主分析问题和解决问题的能力。

譬如，讲解“直线与平面垂直的判定”时，笔者设计了如下实验探究活动：请同学们拿出一张三角形的纸片，自主翻折，并将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触），使得折痕与桌面所在平面能够垂直。学生经过自主翻转后，得出了两种不同的图形，如图1、图2所示。接着，笔者在此基础上提出问题：①如何翻折，才能得到图1中的折痕AD和图2中的折痕DE？②图1和图2两种翻折方法都能使折痕与桌面所在平面垂直，这说明图1和图2两者之间必然存在一定的联系，有着共同的本质特征，那么你认为图1和图2中两者的必然联系和共同的本质特征是什么？引导学生积极思维，自主探究，合作交流，共同研讨，主动概括出直线与平面垂直的判定定理。这样，通过实验探究，不仅提高了学生思维性和创造性，而且点燃了学生探究热情，增强学生自主探究学习能力。

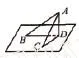
图1

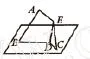
图2

三、鼓励一题多解，发散思维，训练学生思维灵活性

一题多解，即引导学生转换思维视角，多方位、多层次地思考和分析问题，探求出最佳的解题途径。在平时数学教学中，教师要注意关注学生思维的动态生成，鼓励学生一题多解，引导学生多向思考，训练学生思维的变通性和灵活性，提升学生举一反三、触类旁通的能力。

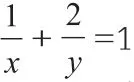
分析：该题看似简单，实际蕴含着多种解题思路，是一道值得探究的习题。

解法一（利用基本不等式进行求解）：

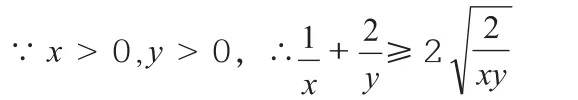
【点评1】开门见山，直接利用基本不等式法得出xy的不等关系，然后再通过化简即可使问题迎刃而解。

解法二（利用均值换元法进行求解）：

【点评2】均值换元法是解不等式、函数、方程等问题至关重要的解题方法之一。通过巧妙换元，可以使数学问题化难为易，化繁为简，得以快速有效解决。

解法三（巧用“1”进行求解）：

【点评3】巧借“1”的妙用，将分式转化为整式，然后探求出有关xy的不等关系，再化简即可求出。

总之，在新课改背景下，高中数学课堂教学中，教师应注意尊重学生的主体地位，聚焦学生思维生成，结合学生学情和学科特点，优选有效策略，引导学生善于观察，勤于思考，乐于探究，敢于质疑，勇于创新，不断迸发数学思维和智慧的火花，从而构建精彩、灵动、高效的数学课堂。

[1]向镒湄.高中生数学提问水平与问题意识和学习策略的关系研究[D].首都师范大学，2012.

[2]郑锵锵.高中生数学问题提出能力及其影响因素的研究[D].东北师范大学，2010.

[3]王甲.关于高中生问题提出能力的调查研究[D].华东师范大学，2009.

[4]罗洁.让素质教育走进数学课堂[J].北京教育，1994（10）.

[5]杨吉成,赵菊生.谈数学教学中“化归”能力的培养[J].北京教育，1994（10）.