利用不对称三线摆测量不规则物体的转动惯量

陈少华 刘艳敏 冷文秀 张国林

(中国石油大学(北京)理学院，油气光学探测技术北京市重点实验室，北京 102249)



利用不对称三线摆测量不规则物体的转动惯量

陈少华 刘艳敏 冷文秀 张国林

(中国石油大学(北京)理学院，油气光学探测技术北京市重点实验室，北京 102249)

工程中常用对称三线摆来测量不规则物体的转动惯量.测量前需预先调整3条摆线严格对称，并保证待测物体和上、下两盘三者的质心严格共线，而三质心共线在实验过程较难严格实现.为此，本文设计并制作了一种不对称三线摆，即将待测物体直接作为下盘，用3根摆线悬挂在上盘上即可.无论3个悬挂点是否对称，也无论摆线是否等长，只要保证3条摆线与质心轴平行，即可测得该物体绕质心轴的转动惯量.实验结果与理论值误差在±5%内的概率为77.78%，表明不对称三线摆可以用于一般刚体的转动惯量测量.

不对称；三线摆；转动惯量

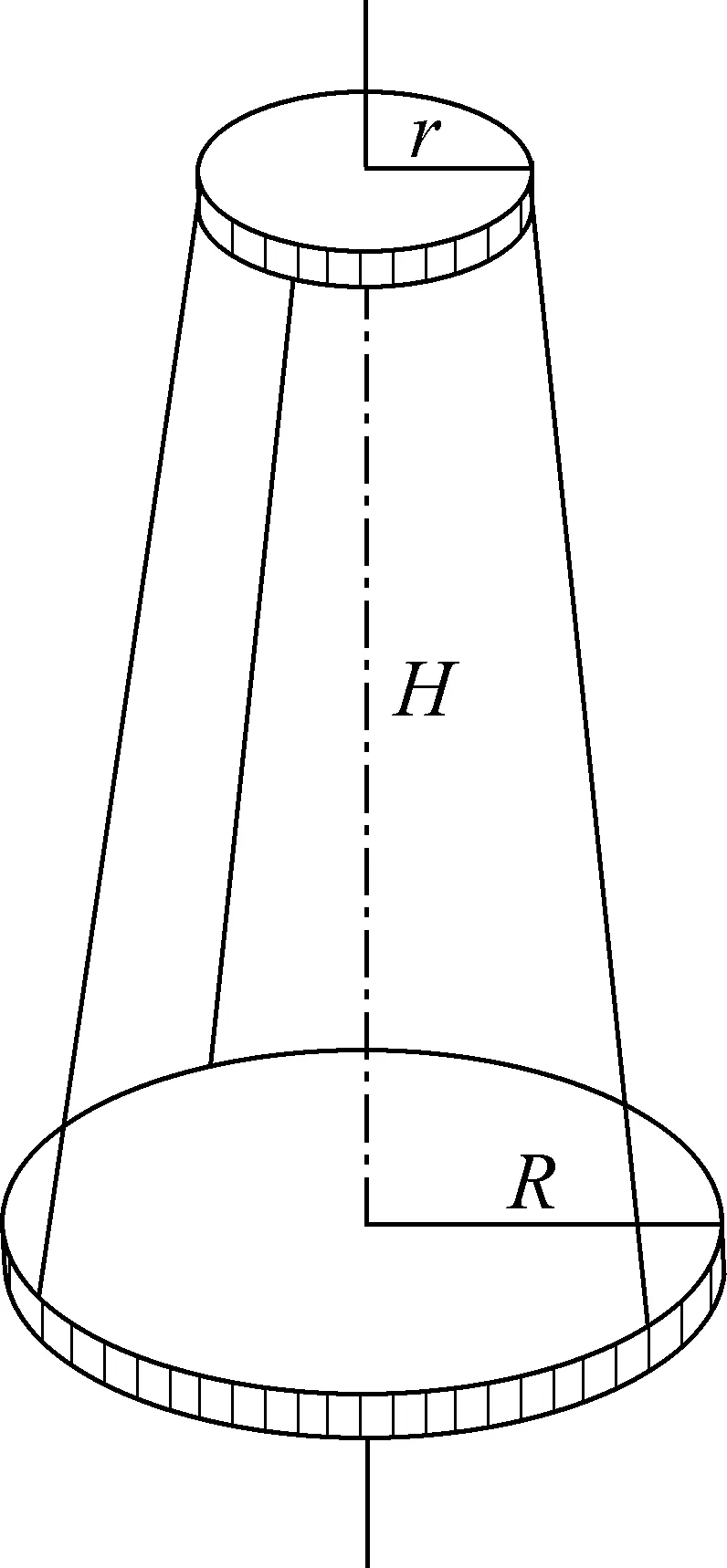
图1 常用对称 三线摆结构图

在工程应用中的许多场合，经常需要测量不规则物体的转动惯量.复摆法[1]、扭摆法[2,3]、三线摆法[4]都是常用的测量方法.由于具有结构简单、直观等优点，三线摆法成为了最为常用的方法，其结构如图1所示[5,6].图1中，该结构用三条等长的细线将一均质大圆盘对称地悬挂在上方小圆盘下.由于悬挂点位置需严格对称，本文中将其称为对称三线摆.测量时，需将待测物体固定在下摆盘上，并保证其质心通过三线摆的竖直质心转轴.而调整上下盘和待测物体三者质心共线是比较困难的.为此，我们设计并制作了一种不对称三线摆，它由3根摆线直接将待测物体悬挂在上盘下方构成.无论3个悬挂点是否对称，也无论摆线是否等长，只要保证3条摆线与系统的质心轴平行，即可直接测量该物体的转动惯量.本文给出了其测量原理，制作了相关的三线摆结构，并成功用于了转动惯量的测量.

1 测量装置及原理

一种不对称三线摆结构，由待测物体直接悬挂在一个托盘上组成，其原理示意图如图2所示.图中O和O′分别为待测物体和上托盘的质心，它们的连线作为旋转轴，并设为z轴，同时在待测物体上建立xOy平面.将3条摆线的长度分别用L1、L2、L3表示，这里的摆线均为不可伸长的轻质细线.另外，托盘和待测物体均可以具有任意的形状.为了方便，图中将其画成了平面.

图2中，待测物体表面的3个吊挂点分别定义为A、B、C，它们至Z轴的水平距离(称为悬距)分别为R1、R2、R3；质心O与3个吊挂点A、B、C在水平面投影两两之间的夹角(称为悬角)分别为φ1、φ2、φ3.若对待测物体施加水平力偶矩，使其偏离平衡位置φ角，之后撤去该力偶矩，则该物体将绕z轴做往复摆动.与图1中的对称三线摆不同，图2中的三线摆只需保证3条摆线与系统质心轴平行即可，而L1、L2和L3，R1、R2和R3和φ1、φ2和φ3均可以取相等或不等的数值，故将其定义为不对称三线摆[5]，显然这种三线摆的设计更加灵活.

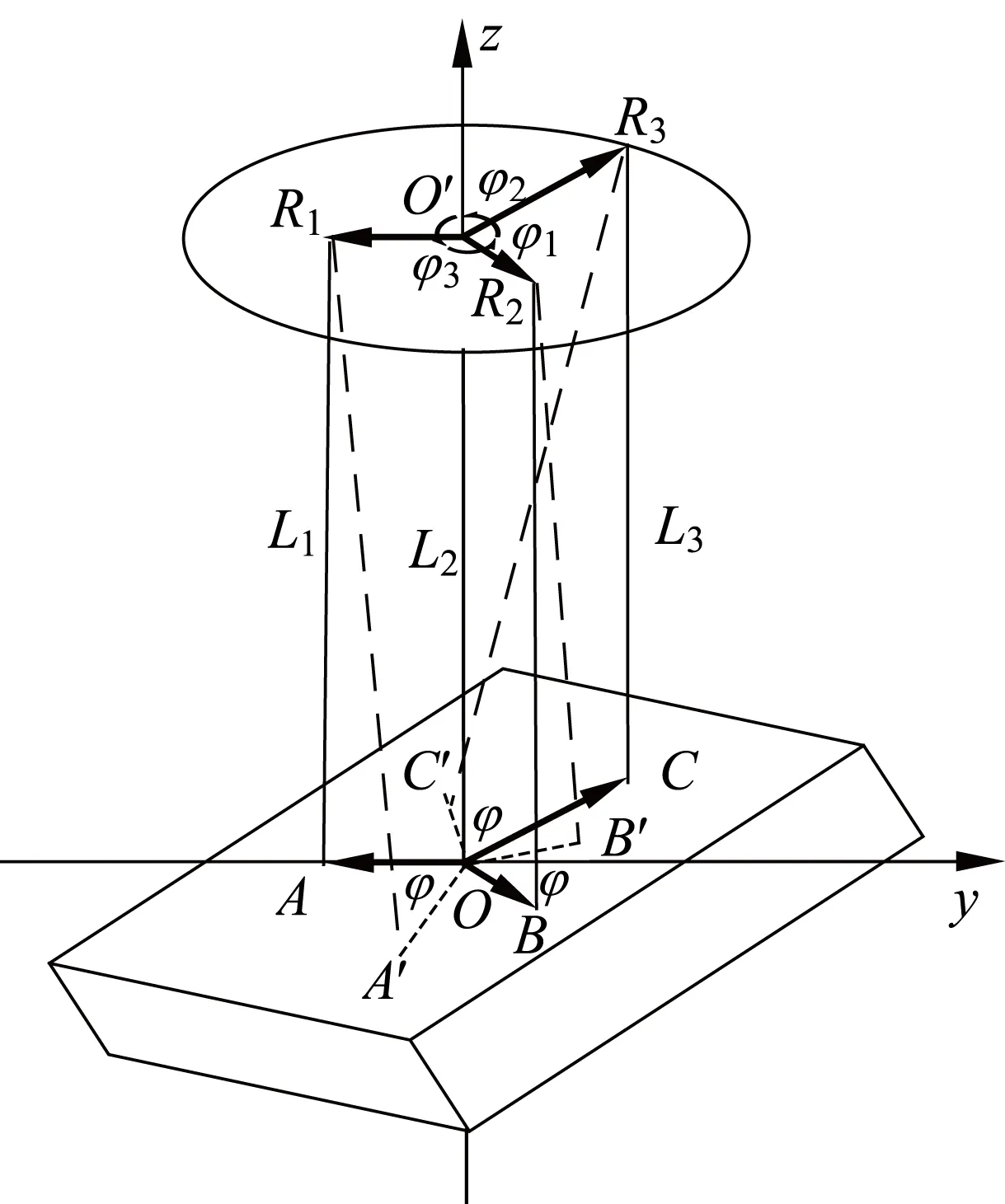
图2 不对称三线摆原理示意图

选用合适的摆线长度，并使最短的摆线长度大于最大悬距20倍，即Lmin> 20Rmax，同时保证摆角φ不是很大，一般小于40°，可以证明，不对称三线摆将做类似复摆的简谐振动.其遵循的一般运动学方程为

(1)

式中，I为三线摆绕z轴旋转的转动惯量，M为定轴转动的合外力矩.

采用定轴转动的动量矩定理和图2中的几何三角关系，可以证明[7]：

式中，m为待测物体的质量,T为摆动周期.

若引入比例系数K

K=

则I可以表示为

I=KmgT2

(3)

2 实验过程与数据处理

待测物体由底座和小齿轮构成，其外观三维图如图3所示.其中，底座为自行设计制作的含5个均匀分布小孔的碳纤维圆盘(圆盘的厚度为4mm)，小齿轮(材料为20CrMn，合金钢)为空心圆柱体结构，如图3中的中间突起部分所示.固定时直接用环氧树脂胶粘贴在碳纤维底座上.实验过程中共采用了直径相同，厚度分别为10mm，12mm，15mm的3个小齿轮.

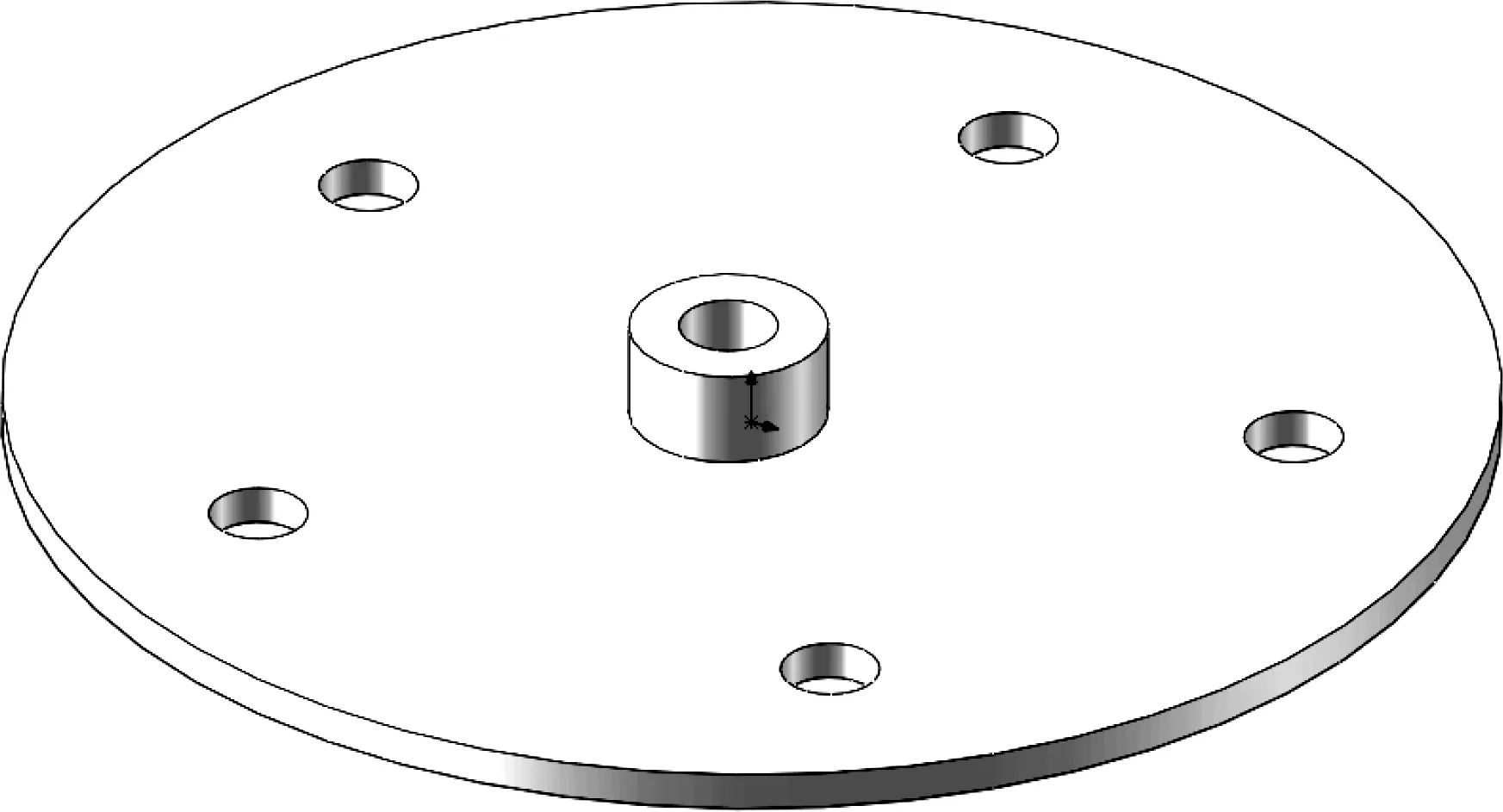
图3 底座和小齿轮的三维结构图

图3中，由于5个小孔和底座质量均为均匀分布，故底座质心即为几何中心.为了表征待测物体质量分布的不规则性，选择固定位置时，特意避开了底座质心，选择在其偏下方某个位置粘贴小齿轮，粘贴后的具体尺寸如图4 (单位：mm) 所示.图中的第1，3，4这3个小孔分别对应其中图2中A、B和C这3个吊挂点的位置，中心的圆孔对应小齿轮.根据图4中的参数，计算了各悬距和悬角的大小并列在表1中.

表1 不对称三线摆的悬距和悬角

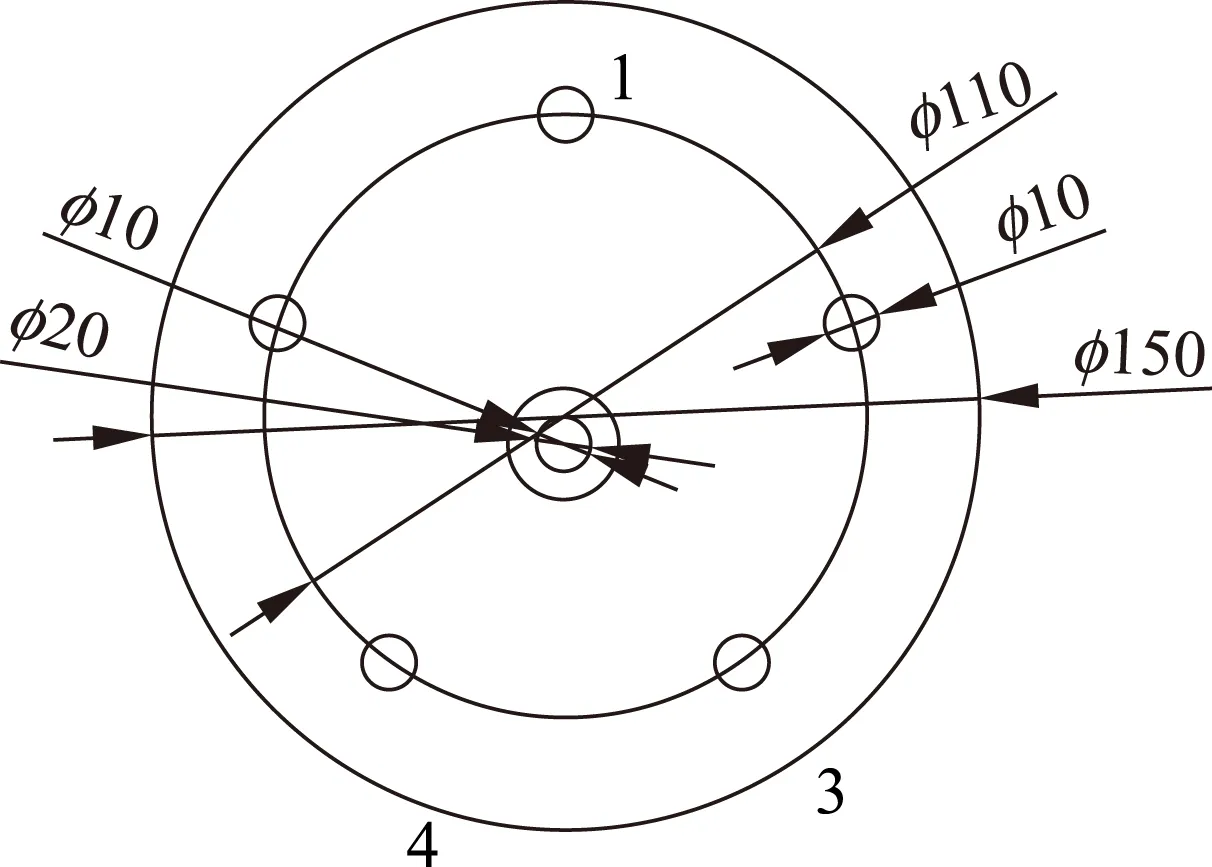
图4 底座和小齿轮的尺寸图

测量过程如下：

(1) 测定待测物体上3个悬挂线的长度L1、L2、L3，若L1=L2=L3，则3个吊挂点组成的三角形恰好位于xOy平面内.若L1≠L2≠L3，用勾股定理可算出3个吊挂点在xOy面上的正投影三角形的各边边长，并画出正投影三角形；

(2) 通过余弦定理求得并标出正投影三角形上待测物体质心投影的位置，用量具在投影三角形上测出R1、R2、R3、φ1、φ2、φ3.

(3) 用计时器——秒表测出摆动周期T，并根据摆角的大小求出相应的K值，同时将得出的悬距、悬角与相关物理量代入公式(2)，便可求得绕质心轴的转动惯量.

为了减小误差，本文中取3条摆线长度相等，同时实验过程中，特别注意对待测物体施加平行的力偶矩，表2为实验结果.

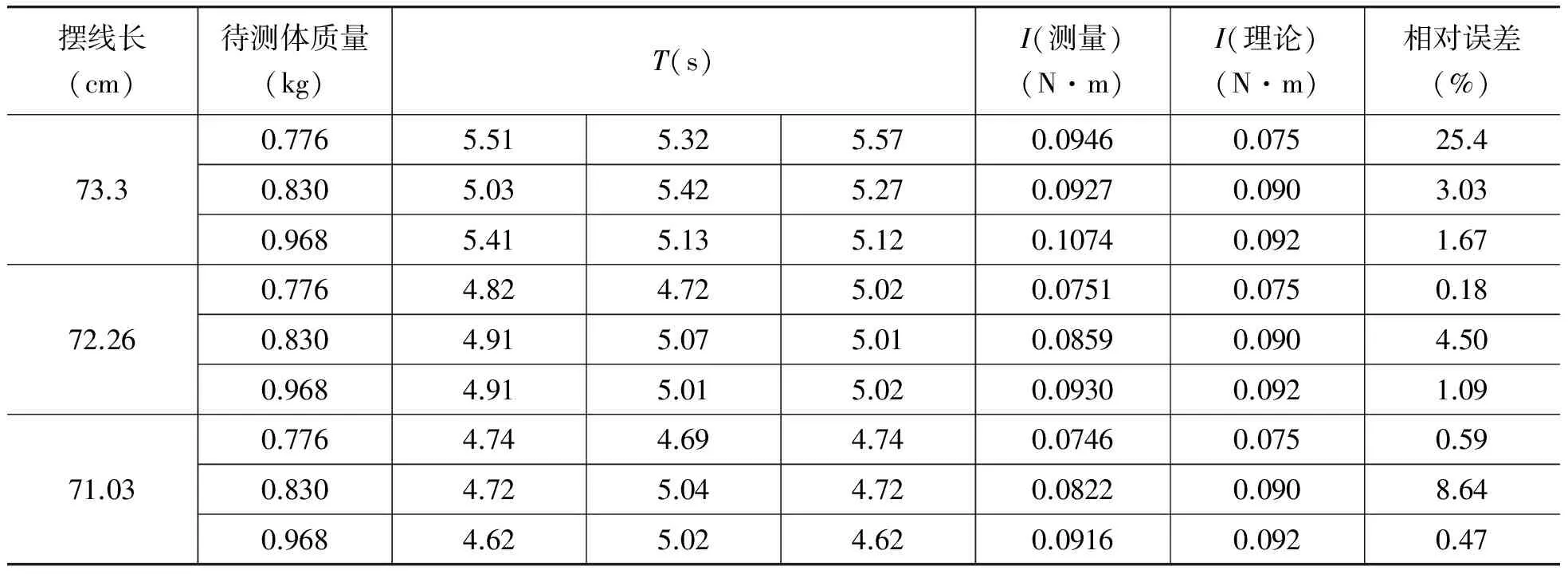
表2 不同摆线长度时待测物体的转动惯量

由表2可以看出，有两次测量的误差较大，而其他7次与理论值的误差均在±5%以内，即实验准确度概率为77.78%，故可以认为，本文设计的三线摆结构可以较为可靠的测量物体的转动惯量.

3 误差分析

通过分析转动惯量I的表达式，可知实验的系统误差主要来源于以下几方面：

(1)R1、R2、R3和φ1、φ2、φ3的测量误差：若3条摆线L1≠L2≠L3；则确定上述6个参数比较繁琐，同时确定过程中也容易引起一些测量误差，故上述实验中我们取L1=L2=L3.

(2) 周期T的误差：由不确定度传递原理可知，仅考虑周期T引起的I的误差为

即I的相对误差会比T大一倍.所以本实验中准确测量振动周期是非常重要的.实验过程中，利用秒表进行了5次等精度测量，并取其平均值作为周期来进行数据处理.如果需要进一步提高测量精度，还可以采用光电开关计时器来测量周期.

(3) 质量的测量误差：由测量天平决定.

(4) 对待测物体施加力偶矩的过程，通常是人为施加的，为了保证三线摆的振动是严格绕着质心轴转动的简谐振动，所以两个力一定要平行且对称施加.表2中有两次测量的实验误差稍大，主要就是施加在待测物体的两个力不对称所致，这也是本装置最主要的误差来源.

(5) 在选定三线摆的质心轴时，需要标定待测物体的质心，一般通过悬挂法确定.同时考虑到摆动的稳定性，建议选择质量分布尽量均匀的物体作为三线摆的下盘，但这并不影响本装置的普适性.

(6) 本实验原理公式成立的前提是长摆线和小角度摆动的情况，即最短的摆线长度大于最大悬距20倍，即Lmin>20Rmax，且摆角一般小于40°，如果摆线长度较短或摆角过大，原理公式将不再成立，测量误差也将比较大.

4 结论

本文利用3根平行摆线将不规则的待测物体悬挂在上托盘的下方，制成了一种测量物体转动惯量的三线摆装置，测量了绕质心轴转动的转动惯量，并与理论值进行了对比，实验与理论误差控制在±5%以内的概率达到了77.78%.最后通过分析实验的误差来源，给出了减小误差的措施.分析表明，只要保证加在待测物体上的力偶矩使其严格绕着系统的质心轴旋转，则这种装置可以快速、准确的进行转动惯量的无损测量.

最后，需要指出的是，本文的测量方法对于对称三线摆测量转动惯量也有一定的借鉴作用.当待测物体固定在下摆盘时，只需找到二者的共同质心，并和上盘的质心一起作为整体的质心轴，也可以进行转动惯量测量.

感谢中国石油大学(北京)优秀青年教师研究项目(2462015YQ0603)和校级教改项目对本文的资助.

[1] 张心明，王凌云，刘建河，等. 复摆法测量箭弹转动惯量和质偏及其误差分析[J].兵工学报，2008，29(4)：450-453. Zhang X M, Wang L Y, Liu J H, et al. The measurement of inertia moment and centroidal deviation of rocket projectile with compound pendulum method and its error analysis[J]. Acta Armamentarii, 2008, 29(4): 450-453.

[2] 唐文彦，李慧鹏，张春富. 扭摆法测量飞行体转动惯量[J].南京理工大学学报，2008，32(1)：69-72. Tang W Y, Li H P, Zhang C F. Measurement of flight object’s moment of inertia using torsion pendulum[J]. Journal of Nanjing University of Science and Technology (Natural Science) 2008, 32(1): 69-72.

[3] 刘振东，郑桂梅，孙兴川. 基于扭摆法的转动惯量测量[J].河南科学，2008，26(10)：1181-1185. Liu Z D, Zheng G M, Sun X C. Rotational inertia measurement using torsion pendulum[J]. Henan Science, 2008, 26(10): 1181-1185.

[4] 姚建安.用三线摆测量转动惯量的研究[J].合肥工业大学学报：自然科学版，1991(4)：74-79. Yao J A. The research of inertia by of measuring three-string the moment pendulum[J]. Journal of Hefei University of Technology, 1991, 14(4): 74-79.

[5] 黄佳峰，赵楠，夏雪琴. 基于三线摆法和Origin7.0软件测定重力加速度新方法的研究[J]. 科技信息，2012(33)：522-524. Huang J F, Zhao N, Xia X Q. Based on three-line pendulum method research on new method for the determination of the gravitational acceleration and origin7.0 software[J]. Science & Technology Information, 2012(33)： 522-524.

[6] 周风琴，李述全，于金华.用三线摆测物体转动惯量的误差分析[J].沈阳大学学报自然科学版，1998(2)：72-74. Zhou F Q, Li S Q, Yu J H. Error analysis of the object inertia with three-line pendulum[J]. Journal of Shenyang University (Natural Science Edition), 1998(2)： 72-74.

[7] 于治会.不规则物体转动惯量的测量方法[J].计量学报，1992，13(1)：45-52. Yu Z H. The measurements of moment of inertia for irregular bodies[J]. Acta Metrology Sinica, 1992, 13(1)： 45-52.

■

MEASUREMENT OF THE ROTARY INERTIA OF AN ARBITRARY OBJECT BASED ON THE IRREGULAR THREE-LINE PENDULUM

Chen Shaohua Liu Yanmin Leng Wenxiu Zhang Guolin

(Science College; Beijing Key Laboratory of Optical Detection Technology for Oil and Gas,China University of Petroleum, Beijing 102249)

To measure the rotary inertia of the object especially in irregular shape, the three-line pendulum is one of the most common candidates in the engineering. In the system, three lines should be symmetrically distributed, while the mass centers of the object and two discs should be pre-adjusted coaxially, which is difficult to realize. So an unsymmetrical three-line pendulum is proposed and manufactured in the article, where the object is suspended to a circular disc with three lines. Whether the three lines are of the same length or not, and whether three hanging positions are symmetrically distributed, if only the three lines are parallel to the centroid axis of the whole system, the rotary inertia of the object could be measured. The probability of the error within 5 percent between the experimental and theoretical rotary inertias would be as high as 77.78 percent, which means the unsymmetrical three-line pendulum is suitable to detect the rotary inertia of the arbitrary object.

unsymmetical; three-line pendulum; rotary inertia

2016-03-07

陈少华，女，副教授，主要从事大学物理教学科研工作，研究方向为光纤传感.shchen@cup.edu.cn

冷文秀，女，讲师，主要从事大学物理教学科研工作，研究方向为太赫兹技术.lengwenxiu@126.com

陈少华，刘艳敏，冷文秀，等. 利用不对称三线摆测量不规则物体的转动惯量[J]. 物理与工程，2016，26(6)：57-60.