圆柱刚体滚动的动力学分析
董焱章 李 鑫 曾红燕
(汽车动力传动与电子控制湖北省重点实验室,湖北汽车工业学院汽车工程系,湖北 十堰 442002)
圆柱刚体滚动的动力学分析
董焱章 李 鑫 曾红燕
(汽车动力传动与电子控制湖北省重点实验室,湖北汽车工业学院汽车工程系,湖北 十堰 442002)
刚体滚动是理论力学中常见的问题,其摩擦力的分析一直受到研究者关注.笔者对圆柱刚体滚子受到任意集中力作用下的运动情况进行了分析,事实上只要圆柱刚体未离开支撑面,起实质作用的只有平行于支撑面的集中力分量,进而得到了相应情形下滚子的角加速度和质心加速度表达式,并研究了滚子角加速度和质心加速度的极值问题,从而提出了摩擦类型判别函数式;并对无摩擦条件下圆柱刚体的滚动状态进行了探讨;最后对滚子静止不动、原地打滑、纯滑动等特殊运动情况作了讨论.
圆柱;刚体滚动;摩擦力;角加速度;质心加速度
Hubei University of Automotive Technology, Shiyan, Hubei 442002)
刚体滚动问题分析一直是理论力学平面运动教学的一个难点.圆柱刚体在运动过程中,存在滑动和滚动两种基本的运动形式,其中摩擦力的分析是关键.摩擦力又分为静摩擦力和动摩擦力.对于圆柱刚体滚动来说,圆柱纯滚动时通常受到静摩擦力的作用,而静摩擦力的方向往往难以直观判断,不少学者对其展开了分析[1-7];圆柱刚体又滚又滑时所受的摩擦力为滑动摩擦力,其方向与接触点处的相对运动方向相反,此时不同于纯滚动时的静摩擦力分析[8-11];此外,研究者还对摩擦力做功[12-15]、侧向摩擦力[16]、支撑面滚动摩阻[17-19]甚至柱面曲率[20]等情形进行了探索.在圆柱刚体滚动的动力学分析中,主动力的大小、方向、作用点都是影响刚体滚动状态的重要因素,研究者对此分析相对较少,本文将从理论力学基本理论[21]出发,分别按照纯滚动和又滚又滑两种运动情形,对圆柱刚体滚子在一般力作用下的动力学问题进行系统分析.
1 问题介绍
如图1所示,初始时刻一质量为m、半径为r的刚性圆柱静止于水平地面上,现施加一力F1作用于A点,使其在地面上发生滚动,已知该力方向与水平方向的夹角为θ,且作用点A与圆柱质心C点的距离为e,圆柱的回转半径为ρ,又圆柱与地面间动、静摩擦因数相等fd=fs=f.试分析圆柱的角加速度α和质心加速度aC.

图1 纯滚动时圆柱的受力分析和运动分析(横截面图)
分析圆柱刚体滚动的角加速度和质心加速度的关键是滚子所受摩擦力方向的判定,下面将按照纯滚动和又滚又滑两种运动情形,系统分析圆柱刚体滚子在任意集中力作用下的动力学问题.
2 圆柱刚体纯滚动情形的动力学分析
如图1所示,此时静摩擦力Fs方向可任设(此处不妨设与F1水平方向分量反向).由刚体平面运动的动力学方程可得
(1)
(2)
(3)
若mg小于F1sinθ,则圆柱会离开地面,而这与其在地面上发生滚动的前提不符,因此圆柱在地面作纯滚动需保证mg大于F1sinθ,此时地面对圆柱有支撑力作用,即FN>0;此时起实质作用的只有平行于地面的集中力水平分量(F1cosθ).
又纯滚动存在运动学关系为
(4)
联立可得圆柱角加速度为
(5)
相应的圆柱质心加速度为
(6)
式(6)表明,θ与e为可分离的因变量,分离后α和aC关于θ为三角函数,而关于e是线性函数.由简单的函数单调性分析可知,当e=r(F1作用于圆柱最高点)且θ=0°(F1水平方向施加)时α(aC)取最大值(θ=180°时,取反向最大值),此时
(7)
特别地,当e=-r(F1作用于B点)或θ=90°(F1竖直方向施加)时,aC=0,α=0,又圆柱初始状态静止,故该条件下圆柱静止不动!
而在e≠-r且θ≠90°时,α方向均取决于θ:θ<90°时,α沿顺时针(图1假设方向);θ>90°时,α沿逆时针;相应的aC方向与集中力水平分量同向.此时由式(5)结合式(3)可得静摩擦力为
(8)
又由|Fs|≤fFN可得圆柱做纯滚动的摩擦条件
(9)
式中,Ψ(θ,e)为摩擦类型判别函数.
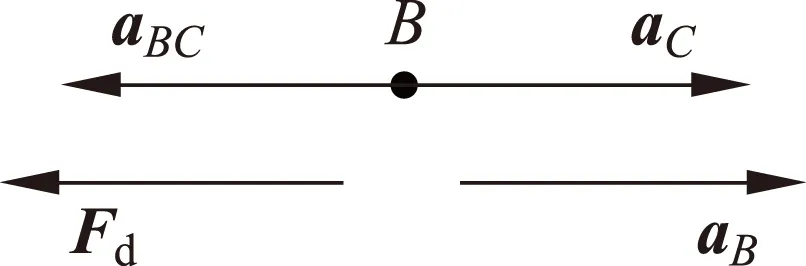
由式(8)可推知:当-r 这里需要对3类特殊情况的动力学分析进行讨论: (1)θ=0°(F1水平方向施加)此时前述结论式可退化为 (10) (11) 相应的参数特征与文献相关阐述[21]保持一致. (2)e=0(F1作用于圆柱质心)此时相应结论式可退化为 (12) (13) 此时α、aC、Fs均关于θ为余弦函数. (3)f=0(地面光滑)此时刚体平面运动的动力学方程退化为 (14) (15) 进而可直接求得 (16) 可知,当且仅当e=ρ2/r时,才能满足圆柱作纯滚动的运动学关系式aC=rα,这恰好是纯滚动摩擦条件(9)的特例. 圆柱又滚又滑时受到滑动摩擦力,而滑动摩擦力是以绝对值出现在动力学方程中,因此需要分左、右两种情形预设滑动摩擦力的方向. 3.1 滑动摩擦力方向向左(如图2所示) 图2 又滚又滑时圆柱的受力分析和运动分析 (滑动摩擦力向左) (17) 同样地,要使圆柱在地面上又滚又滑,也需保证mg大于F1sinθ,即FN>0;对于又滚又滑,也存在库伦定律 Fd=fFN (20) 联立可得,圆柱的角加速度为 (21) 圆柱的质心加速度为 (22) 令α=0,得 (23) 令aC=0,得 (24) (1) 若α=0,aC=0,又圆柱初始状态静止,此时圆柱静止不动; (2) 若α≠0,aC=0,此时圆柱原地打滑,有 (25) (3) 若α=0,aC≠0,此时圆柱纯滑动(平动),有 (26) 将式(22)对θ求一阶导,得 (27) 令式(27)等于零,可得, (28) 又aC关于θ的三角函数关系如图3所示,可知当θ=arctanf时,aC取正向最大值,有 (29) 图3 质心加速度aC随θ变化的函数图 而当θ=π+arctanf时,aC取反向最大值,有 (30) 类似式(6)的分析,由式(21)可知,α在(0°,r)及(180°,-r)处均取最大值,即 (31) 由前提条件(圆柱受到向左的滑动摩擦力),加之圆柱初始时刻速度为零,因此地面接触点B有向右滑动的趋势,如图4所示,aB=aC+aBC方向向右为 (32) 从而可得圆柱受到向左的滑动摩擦力条件为 (33) 动摩擦因数f为非负值,因此式(33)右边需要保证为正,即θ≠90°、e≠ρ2/r且当0°≤θ<90°时,-r ≤e <ρ2/r,当90°<θ ≤180°时,ρ2/r 图4 B点加速度矢量合成图 同样地,这里也对3类特殊情况的动力学分析展开讨论: (1) θ=0°(F1水平方向施加)此时相应地前述结论式可退化为 (34) (35) (2) e=0(F1作用于圆柱质心)此时相应地前述结论式可退化为 (36) (37) (3) f=0(地面光滑)此时刚体平面运动的动力学方程退化为 (38) 最后的情形(3),若e=0,则α=0,aC≠0,即圆柱作纯滑动(平动)! 3.2 滑动摩擦力方向向右(如图5所示) 图5 又滚又滑时圆柱的受力分析和运动分析 (滑动摩擦力向右) 与滑动摩擦力Fd方向向左情形相比,摩擦力方向向右的情形需要对涉及Fd的平衡方程相应项作反号处理,故情形3.1含有“f”的结论只需做同样的反号处理即可适应于情形3.2,此时,保证圆柱刚体受到向右滑动摩擦力的条件为 (39) 初始静止在地面的圆柱刚体,在任意集中力作用下滚动,若已知刚体所受主动力的大小(F1)、方向(θ)、作用点(e)及其自身相关物理参数(m、r、ρ)时,通过比较摩擦因素f与摩擦类型判别函数Ψ(θ,e)的大小关系,即可快速判定圆柱所受摩擦力的情形,进而确定圆柱刚体滚动的动力学运动量(质心加速度和角加速度): (1) 当f≥|Ψ(θ,e)|时,圆柱作纯滚动,一般存在静摩擦力,其方向取决于作用点的位置、圆柱体半径及惯性矩等因素,但静摩擦力的存在并不是圆柱作纯滚动运动的必要条件,在光滑地面上,满足条件(e=ρ2/r)的圆柱刚体依旧可作纯滚动; (2) 当f<Ψ(θ,e)时,圆柱作又滚又滑,动摩擦力方向与主动力的水平分量同向,并得到了圆柱刚体静止不动、原地打滑、纯滑动等特殊情况的摩擦条件; (3) 当f<-Ψ(θ,e)时,圆柱作又滚又滑,动摩擦力方向与主动力的水平分量反向,此时与情形(2)类似,相应的公式中摩擦因数f反号. [1] 屠广霖.关于滚动问题中的静摩擦力[J].物理通报,1964(4):183-185.TuGL.Thestaticfrictionforceontherollingproblem[J].PhysicsBulletin, 1964(4): 183-185. [2] 刘涛,程富华.滚动物体所受静摩擦力的方向问题[J].物理教学,1979(3):1-3.LiuT,ChengFH.Directionofstaticfrictionofrollingobjects[J].WuLiJiaoXue, 1979(3): 1-3. [3] 卢国生.保持滚动无滑动的条件[J].大学物理,1983(9):17-22.LuGS.Conditionsforkeeprollingwithoutsliding[J].CollegePhysics, 1983(9): 17-22. [4] 陈景鵰.浅析滚动问题中的静摩擦力[J].江西农业大学学报,1992,14(2):186-188.ChenJD.Briefanalysisofstaticfrictioninrollingsituation[J].ActaAgriculturaeUniversitatisJiangxincnsis, 1992, 14(2): 186-188. [5] 梁志强. 刚体纯滚动时静摩擦力方向的判据[J].物理通报,1997(12):10-11.LiangZQ.Criterionofstaticfrictionforceinpurerolling[J].PhysicsBulletin, 1997(12): 10-11. [6] 李惠玲,郭志俊.纯滚动刚体所受静摩擦力的方向[J].山西师大学报(自然科学版),1998,12(1):43-45.LiHL,GuoZJ.Thedirectionofstaticfractionalforceexertedtopurerollingrigidbody[J].JournalofShanxiTeachers’University, 1998, 12(1): 43-45. [7] 姜芳,赵东.纯滚动圆轮静摩擦力方向的确定[J].力学与实践,2011,33(1):86-88.JiangF,ZhaoD.Determinationofstaticfrictionforceofpureroller[J].MechanicsinEngineering, 2011, 33(1): 86-88. [8] 古月.圆环滚动中所受的摩擦力[J].蒙自师专学报,1988,5(2):60-63.GuY.Frictionintheringrolling[J].JournalofMengziTeachers’Institute, 1988, 5(2): 60-63. [9] 凌余林.刚体平面滚动摩擦力的分析[J].河池师专学报(理科版),1994,14(3):42-43.LingYL.Analysisofrollingfrictionforceofrigidbody[J].JournalofHechiTeachersCollege, 1994, 14(3): 42-43. [10] 宁雅丽.滚动问题中摩擦力的研究[J].兰州工业高等专科学校学报,2008,15(2):52-54.NingYL.Researchoffrictioninrotationproblems[J].JournalofLanzhouPolytechnicCollege, 2008, 15(2): 52-54. [11] 彭瑞东,周宏伟,黎立云.滚动问题中摩擦力的判断[J].力学与实践,2010,32(5):83-86.PengRD,ZhouHW,LiLY.Judgmentoffrictioninrolling[J].MechanicsinEngineering, 2010, 32(5): 83-86. [12] 陈晓白.对摩擦力的再认识——滚动问题中摩擦力的功[J].大庆高等专科学校学报,1994,14(4):38-39.ChenXB.Reunderstandingoffriction——Theworkoffrictioninrolling[J].JournalofDaqingCollege, 1994, 14(4): 38-39. [13] 胡辉.无滑动滚动时摩擦力的功[J].力学与实践,2001,23(4):64-65.HuH.Theworkoffrictionwithoutslidingrolling[J].MechanicsinEngineering, 2001, 23(4): 64-65. [14] 周雨青,叶兆宁,彭毅.纯滚动运动中的摩擦力做功问题[J].物理与工程,2004,14(5):31-33.ZhouYQ,YeZN,PengY.Theworkbyfrictioninpurerolling[J].PhysicsandEngineering, 2004, 14(5): 31-33. [15] 刘大为,牛福龙.纯滚动轮所受静摩擦力方向的确定[J].甘肃联合大学学报(自然科学版),2008,22(6):51-53.LiuDW,NiuFL.Thedetermineofthestaticfrictiondirectionofapurerollingwheel[J].JournalofGansuLianheUniversity(NaturalSciences), 2008, 22(6): 51-53. [16] 冯永伟.汽车转向时纯滚动轮胎侧向摩擦力分析研究[J].机械制造与自动化,2004(6):40-42.FengYW.Theresearchofthemotorturningtimepurerollingtiresidefriction[J].MachineBuildingandAutomation, 2004(6): 40-42. [17] 唐红度.滚动摩擦力计算中弹性滞后系数的确定[J].力学与实践,2003,25(5):76-77.TangHD.Determinationofelastichysteresisinrollingfrictioncalculation[J].MechanicsinEngineering, 2003, 25(5): 76-77. [18] 王嘉航.圆环滚动时摩擦力的分析[J].淮阴工学院学报,2012,21(1):28-30.WangJH.Onthefrictionofcircularringinrolling[J].JournalofHuaiyinInstituteofTechnology, 2012, 21(1): 28-30. [19] 王海军.对滚动摩擦力成因的深入思考[J].物理教学探讨,2015,33(4):43-44.WangHJ.Deepthinkingonthecauseofrollingfriction[J].JournalofPhysicsTeaching. 2015, 33(4): 43-44. [20] 周国全.凸柱体表面缠绕软绳的横向摩擦力的曲率无关性[J].物理与工程,2015,25(3):38-40.ZhouGQ.CurvatureIndependenceofthetransversefrictionbetweenasoftropeandthesurfaceofaconvexcolumn[J].PhysicsandEngineering, 2015, 25(3): 38-40. [21] 胡运康,景荣春.理论力学[M].北京:高等教育出版社,2006. 审稿人意见摘录: 1. 作者对圆柱刚体滚子受到任意集中力作用下的运动分情况进行了完整讨论,对该内容教学有一定的意义; 2. 两个参量e和θ是可分离因素,而且分离之后对e是线性函数,对θ是三角函数;这两者的极值都无需要求导。这样分析的数学成本就低多了,文字也会简洁一些; 3. 只要圆柱没离支撑面,应该起作用的是力平行于支撑面的分量在起作用; 4. 其他见批注稿(请仔细斟酌). ■ DYNAMIC ANALYSIS FOR THE ROLLING OF CYLINDRICAL RIGID BODY Dong Yanzhang Li Xin Zeng Hongyan (Hubei Key Laboratory of Automotive Power Train and Electronic Control, Department of Automobile Engineering, Rolling of rigid body is a common problem in theoretical mechanics, and the analysis of friction has attracted researchers. In this paper, a cylindrical rigid roller under an arbitrary concentrated load is analyzed according to different cases. In fact, as long as the cylindrical rigid roller is not away from its support, only the parallel component of the concentrated load plays an essential role. Then the angular acceleration and the acceleration of mass center of the roller are derived, and their extreme value results are obtained. Sequentially the general form of friction discrimination function is proposed. Rolling state of cylindrical rigid body under the frictionless case is also explored. Finally, statics, in-situ slipping, pure sliding and other special movement cases are discussed. cylinder; rigid body rolling; friction force; angular acceleration; acceleration of mass center 2016-03-16 国家自然科学基金青年科学基金(11502075),湖北省自然科学基金(2014CFB629),湖北汽车工业学院博士科研启动基金(BK201501)资助项目. 董焱章,男,讲师,主要从事工程力学、结构与多学科优化、超材料设计等方面的研究.dongyz@huat.edu.cn 董焱章,李鑫,曾红燕. 圆柱刚体滚动的动力学分析[J]. 物理与工程,2016,26(6):34-38.3 圆柱刚体又滚又滑情形的动力学分析




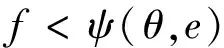

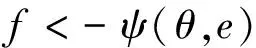
4 结语

