复杂轨道高程误差下钢箱梁滑移受力敏感性研究

袁鹏，李德建，陆尧，李传习

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 长沙理工大学 土木与建筑学院，湖南 长沙 410076)

复杂轨道高程误差下钢箱梁滑移受力敏感性研究

袁鹏1，李德建1，陆尧1，李传习2

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 长沙理工大学 土木与建筑学院，湖南 长沙 410076)

为了获得钢箱梁复杂轨道滑移过程中各种极端情况下结构受力及变形敏感性结果，运用有限元软件ANSYS，建立考虑面-面接触效应的钢箱梁和轨道有限元模型，对嘉绍大桥无索区钢箱梁复杂轨道滑移过程中的2个最不利工况进行结构受力及变形敏感性分析并讨论各工况下的误差控制标准。研究结果表明：在钢箱梁复杂轨道滑移过程中，滑块支反力、结构变形及应力对轨道底约束方式和轨道高程误差比较敏感；滑块处轨道底约束方式相同时，轨道架设对角高程误差不应超过5 mm，极限误差不能超过8 mm；滑块处轨道底约束方式不同时，轨道高程误差不应超过2 mm，极限误差不能超过4 mm；轨道底约束刚度越大支反力对高程误差越敏感、强约束处的支反力分配比较大、支反力增长率较快，且容易发生面外屈曲。

桥梁工程；复杂轨道；敏感性分析；轨道高程误差；应力变化幅值

结构施工过程中，不可避免地造成各种施工误差。国内外学者对结构施工误差进行了大量研究[1-6]，并将现代控制论与工程实践相结合，先后提出了较为成熟的误差控制理论[7-8]。但对于临时支架结构误差作用下结构受力性能的研究较少[9-10]，规范[11]仅对临时支架结构最大变形允许值做了规定。实际结构施工中，临时支架结构误差对其使用阶段内力、应力和变形等的影响也是一个非常值得关注的问题。

1 工程概况

嘉绍大桥主航道桥是世界上首座六塔四索面分幅式独柱钢箱梁斜拉桥(如图1)，其无索区钢箱梁采用满堂支架施工。支架上部分别采用双拼HM588型钢及单层5组贝雷片作为横移和纵移轨道主梁，钢管桩桩顶与轨道底固结，使支架和轨道系统具有足够的刚度和整体稳定性。轨道顶设3×I25a工字钢作为移梁滑道并涂上润滑剂，以保证箱梁顺利滑移(如图2～3)。

钢箱梁通过桥面吊机起吊置于两对滑块上，滑块与钢箱梁横隔板相对应(如图3)。采用钢绞线牵引箱梁使其与滑块一起在轨道上缓慢滑移到位。移梁过程中存在如钢箱梁梁底与滑块支座接触存在时差、滑块处轨道底有无钢管桩约束等滑移不利情况。可能导致移梁轨道梁变形过大或局部应力超过材料强度设计值、滑块脱空或滑移过程中脱轨的现象以及滑块处钢箱梁局部失稳等。所以钢箱梁滑移中钢箱梁底板和轨道各接触对之间的应力大小及变化幅值、结构变形量、各滑块支反力等的研究对保证安全施工具有重要意义。

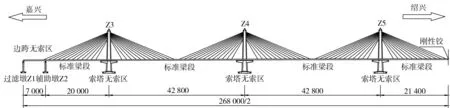
单位：cm图1 嘉绍大桥斜拉桥纵向1/2立面布置图Fig.1 Elevation of Jiashao Cable-stayed bridge 1/2

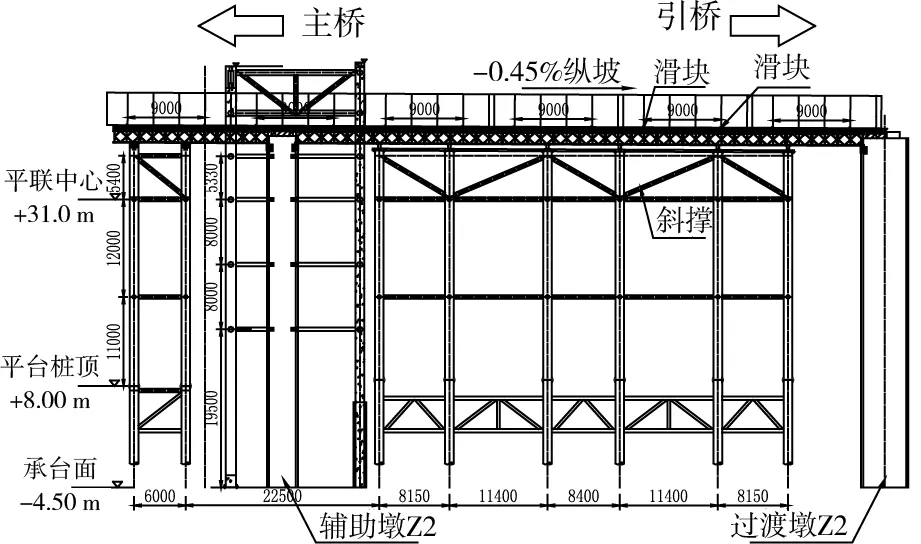
单位：mm图2 边跨无索区支架及移梁轨道立面布置图Fig.2 Elevation of side span non-stayed cable segment and shifting the beam orbit

单位：mm图3 边跨无索区支架及移梁轨道平面布置图Fig.3 Plan of side span non-stayed cable segment and shifting the beam orbit plane

2 空间有限元模型

2.1 最不利工况选取

选取滑移过程中最不利的2种工况对结构进行受力敏感性研究(如图4)。工况1(轨道对角高程误差工况)：轨道底相同约束方式下的移梁工况，取2和3号滑块处轨道高程低于1和4号滑块处轨道高程分别为-5，-8和-10 mm进行结构受力敏感性分析；工况2(强约束高程误差工况)：轨道底不同约束方式下的移梁工况，将2和4号滑块置于钢管桩桩顶轨道上，1和3号滑块处轨道底悬空，并取2号滑块处轨道顶面高程误差分别为0，-2和-4 mm进行结构受力敏感性分析。

2.2 模型建立

采用ANSYS中壳单元SHELL181建立边跨无索区B1梁段和移梁轨道段有限元模型，钢箱梁底板处接触面采用conta173模拟，轨道处目标面采用targe170模拟，且假定接触对之间为理想粗糙接触，法向接触刚度取为1.0，接触对自动闭合初始间隙[12-13]。支架系统具有足够的刚度和整体稳定性且完成了预压，故不计支架体系变形对滑移造成的影响。通过约束钢管桩上方轨道底面3个平动自由度，来拟轨道底支架刚体系统(如图4)。2个计算工况中仅对钢箱梁一端粱端UZ(纵桥向)，UX(横桥向)位移，另一端粱端UX位移进行约束，以保证结构计算方程正定(如图5)。

图4 移梁轨道有限元模型Fig.4 Finite element model of shifting the beam orbit

图5 B1梁段有限元模型Fig.5 Finite element model of B1 beam

3 轨道对角高程误差结果分析

3.1 滑块支反力结果及分析

图6为支反力敏感性计算结果，可知：各滑块支反力分配对对角高程误差较敏感，对角滑块支反力增长率与递减率基本相同；当高程误差为5 mm时，各滑块支反力稍不均匀，当高程误差为8 mm时，轨道接近于2点受力(1和4号滑块支反力占钢箱梁总重的88.8%)，当高程误差为10 mm时，2和3号滑块与箱梁底板已脱空。故轨道底相同约束方式下滑块支反力控制对角高程误差应取为5 mm，极限对角高程误差为8 mm，箱梁与滑块脱空对角高程误差为10 mm。

图6 滑块支反力变化Fig.6 Change chart of slide support reaction

3.2 变形结果及分析

为了分析轨道挤压变形(轨道侵入量)[14-15]，假定：轨道侵入量=接触对目标面位移-轨道挠曲位移。

图7～8为变形敏感性计算结果，可知：各接触对竖向位移、目标面对角位移差对对角高程误差较敏感，当误差为5 mm时，接触对目标面位移值均在7～9 mm范围，最大侵入量也相差不大；当误差为8 mm时，1和4号接触对侵入量远大于2和3接触对，挤压变形也更明显，钢箱梁难以完成滑移工作；当误差达10 mm时，2和3号接触对已经脱空，已不能完成钢箱梁滑移工况。故轨道底相同约束方式下轨道变形及侵入量控制对角高程误差应取为5 mm，极限对角高程误差为8 mm，箱梁与滑块脱空对角高程误差为10 mm。

图7 目标面位移变化Fig.7 Change chart of target surface displacement

图8 接触面侵入量变化Fig.8 Change chart of interface penetration

3.3 局部稳定及强度分析

表1和图9为对角高程变化时结构应力敏感性计算结果(仅列出8 mm对角高程误差计算结果)，可知：钢箱梁底板和轨道接触对处结构应力对高程误差较敏感；随着高程误差的增大，1和4号

接触对应力幅值逐渐增加，挤压变形增大，2和3号接触对应力幅值逐渐减小，滑块逐渐脱空。当误差为5 mm时，结构应力均在材料强度允许值范围内，且所占面积较小；当误差为8 mm时，结构应力已超过了轨道材料强度设计值，1和4号接触对处结构应力最大值分别为217 MPa和215 MPa，且所占面积较大；当误差为10 mm时，结构应力已超过了材料强度设计值，1和4号接触对处结构应力最大值分别为238 MPa，239 MPa，变形较大，第1阶屈曲发生在1和4号滑块对应的钢箱梁横隔板处，为平面外屈曲，屈曲系数为6.531[16]；故轨道底不同约束方式下轨道材料强度控制对角高程误差应取为5 mm，极限对角高程误差为8 mm，箱梁与滑块脱空对角高程误差为10 mm。

表1 8 mm对角高程误差接触对应力值Table 1 Contact pairs stress of 8 mm diagonal elevation error MPa

注：表中应力指应力幅值,比例指代最大值所占百分比

(a)钢箱梁底板应力云图；(b)轨道应力云图图9 8 mm轨道对角高程误差结构应力云图Fig.9 Structrue stress nephogram of 8 mm

4 强约束高程误差结果分析

4.1 滑块支反力结果及分析

由图10可知：各2滑块支反力对高程误差很敏感，1号、4号滑块支反力增长率均大于3号滑块，4号滑块支反力增长幅值最大，3号滑块支反力增长幅值最小，2号滑块支反力迅速减小直至脱空形成3点受力；当无轨道高程误差时，各滑块支反力为1∶1.82∶1.06∶1.7，滑块支反力稍不均匀；当轨道高程误差为2 mm时，2号滑块支反力迅速减小，4号滑块支反力是2号滑块支反力的2.92倍，各支反力分配较不均匀，但仍能完成钢箱梁滑移；当高程误差增至4 mm时，2号滑块已与箱梁脱空，形成3点受力，其中1和4号支反力占箱梁总重的75.6%。故轨道底约束越强支反力对高程误差越敏感、强约束滑块支反力分配比越大、支反力增长率越大，轨道底不同约束方式下滑块支反力控制高程误差应取为2 mm，箱梁与滑块脱空的轨道极限高程差为4 mm。

图10 滑块支反力变化Fig.10 Change chart of slide support reaction

4.2 变形结果及分析

图11～13为变形敏感性计算结果(截取工况2所在钢管桩间轨道段)，可知：随着高程误差的增大，2号接触对轨道侵入量逐渐减小即发生轨道支反力卸载过程，1，3和4号接触对侵入量逐渐增加，其中1和4号接触对侵入量增长率大于3号接触对，且接触对侵入量均大于3号；当误差为2 mm时无滑块脱空、侵入量相差不大，接触良好，当误差达到4 mm时，2和4号接触对侵入量差达0.77 mm，此时2号滑块卸载完成形成3点受力，若仍进行移梁施工可能发生滑块脱轨、钢箱梁倾覆等事故。由变形云图13可知：1和3号接触对处轨道顶面变形比较大(含轨道挠曲变形)，4号接触对处箱梁底板变形比较大。由2 mm高程误差屈曲计算结果知。故轨道底不同约束方式下：强约束处箱梁底变形比较大，侵入量小，弱约束处轨道变形比较大；轨道变形及侵入量控制对角高程误差应取为2 mm，轨道与滑块侵入量极限高程差应取为4 mm。

图11 目标面位移变化Fig.11 Change chart of target surface displacement

图12 接触面侵入量变化Fig.12 Change chart of interface penetration

(a)钢箱梁底板变形云图；(b)轨道变形云图图13 变形云图Fig.13 Deformation stress nephogram

4.3 局部稳定及强度分析

表2和图14为高程变化时接触对应力及结构应力云图计算结果(仅列出2 mm高程误差计算结果)，可知：对于钢箱梁底板，随着高程误差的增加，最大应力逐渐增大，最大应力分别为107，123和140 MPa，但均没有超过Q345钢材的材料强度设计值，最大应力位置由2号接触对处的底边U肋直板转移到4号接触对处的底边U肋直板处，所占面积很小，结构安全；对于轨道，随着高程误差的增加，最大应力逐渐增大，分别为117，136和155 MPa，且均没有超过Q235钢材的材料强度设计值，位于4号滑块对应轨道处的轨道顶板与腹板处，所占面积逐渐增大但仍较小、结构安全，移梁仍能顺利进行；对于接触对，随着高程误差的增加，1，3和4号接触对应力变化幅值逐渐增大，最大应力所占比例也越大并向3点接触过度。当误差为4 mm时，2号接触对已大部分脱空，箱梁已不能在轨道上滑移，第1阶屈曲发生在2号滑块对应的钢箱梁横隔板处，且为平面外屈曲，屈曲系数为4.032，移梁不安全。故轨道底不同约束方式下轨道材料强度控制高程误差应取为2 mm，极限高程差应取为4 mm。

表2 2 mm高程误差接触对应力值Table 2 Contact pairs stress of 2 mm elevation error MPa

注：表中应力指应力幅值,比例指代最大值所占百分比

(a)钢箱梁底板应力云图;(b)轨道应力云图图14 2 mm轨道高程误差结构应力云图Fig.14 Structrue stress nephogram of 2 mm track elevation error

5 结论

1)轨道底相同约束方式下轨道架设对角高程控制误差应在5 mm以内，极限对角高程误差应取为8 mm，轨道与滑块脱空的对角高程差为10 mm，当对角高程误差达到10 mm时，低高程处滑块已脱空，接触对应力已超出材料强度设计值，且最大应力所占面积较大，结构安全施工已没有保证；

2)轨道底不同约束方式下轨道架设高程控制误差应取为2 mm、极限高程差应取为4 mm，当高程误差达到4 mm时，低高程处滑块已脱空，移梁施工已不能完成；

3)轨道底约束越强支反力对高程误差越敏感，且强约束处支反力分配比例大、支反力增长率大；

4)轨道底不同约束方式下，强约束处箱梁底变形比较大，弱约束处轨道变形比较大，且均容易发生面外屈曲；

5)对于钢箱梁复杂轨道滑移对轨道高程误差精度要求较高，施工中应严格控制放样精度，同时采用多点自平衡同步滑移液压系统纠正误差。

[1] 郝超. 大跨度钢斜拉桥施工误差调整方法研究[J]. 浙江大学学报(工学版),2003,37(3):54-57. HAO Chao. Study on construction error adjustment method of long-span steel cable-stayed bridge [J]. Journal of Zhejiang University (Engineering Science), 2003,37(3):54-57.

[2] Sim J, Lee K, Kim H, et al. Structural assessment for high concrete pier with a vertical construction error and suggestion of the improvement measurement[C]// 6th International Conference on Bridge Maintenance, Safety and Management (IABMAS), Stresa, Italy, 2012.

[3] 杜迎东, 王起才, 张戎令, 等. 系杆拱桥拱肋内混凝土非对称浇筑量化影响分析[J]. 铁道科学与工程学报,2015,12(6):1394-1400. DU Yingdong, WANG Qicai, ZHANG Rongling, et al. Quantitative analysis on asymmetrical pouring of concrete in the arch rib of tied arch bridge[J]. Journal of Railway Science and Engineering, 2015,12(6):1394-1400.

[4] 田广宇, 郭彦林, 张博浩, 等. 宝安体育场车辐式屋盖结构施工误差敏感性试验及误差限值控制方法研究[J]. 建筑结构学报,2011,32(3):11-18. TIAN Guangyu, GUO Yanlin, ZHANG Bohao,et al. Experiment on sensitivity to construction tolerance and research on tolerance control criteria in spoke structural roof of Bao’an Stadium [J]. Journal of Building Structures, 2011,32(3):11-18.

[5] 杜闯, 丁红岩, 张浦阳, 等. 斜跨曲线异形拱桥施工过程应力和挠度分析[J]. 铁道科学与工程学报,2015,12(5):1130-1135. DU Chuang, DING Hongyan, ZHANG Puyang, et al. Analysis of the stress and deflection of diagonal-span curve special shaped arch bridge during[J]. Journal of Railway Science and Engineering,2015,12(5):1130-1135.

[6] 郭彦林, 田广宇, 张博浩, 等. 基于一次二阶矩可靠度指标的车辐式结构索长误差控制限值研究[J]. 建筑科学与工程学报,2010,27(4):69-77. GUO Yanlin, TIAN Guangyu, ZHANG Bohao,et al. Research on deviation control of cable’s length in spoke structures based on first-order-second-moment reliability index[J]. Journal of Architecture and Civil Engineering, 2010,27(4):69-77.

[7] Guan H, Chen D W. Stochastic analysis of prestressed concrete cable-stayed bridges considering construction errors[C]//International Conference on Civil Engineering and Building Materials (CEBM),Kunming, 2011.

[8] 李乔, 卜一之, 张清华. 基于几何控制的全过程自适应施工控制系统研究[J]. 土木工程学报,2009,42(7):69-77. LI Qiao, BU Yizhi, ZHANG Qinghua. Whole-procedure adaptive construction control system based on geometry control method [J]. China Civil Engineering Journal, 2009,42(7):69-77.

[9] 王卫锋, 林俊锋, 马文田. 顶推施工中临时墩位置对梁体制造误差的影响[J]. 华南理工大学学报(自然科学版),2006,34(9):76-79,89. WANG Weifeng, LIN Junfeng, MA Wentian. Effect of location of temporary pier in incremental launching construction on manufacture error of girder[J]. Journal of South China University of Technology (Natural Science Edition), 2006,34(9):76-79,89.

[10] WANG Guangyue, LIU Jian, FAN Qi. Construction monitoring of long span continuous rigid frame box girder bridge[C]// International Conference on Structures and Building Materials,Guangzhou, 2011.

[11] JTG/T F50—2011,公路桥涵施工技术规范[S]. JTG/T F50—2011, Technical specifications for construction of highway bridges and culverts[S].

[12] 王满生, 周锡元, 胡聿贤. 桩土动力分析中接触模型的研究[J]. 岩土工程学报,2005,27(6):616-620. WANG Mansheng, ZHOU Xiyuan, HU Yuxian. Studies on contact model of soil-pile dynamic interaction[J]. Chinese Journal of Geotechnical Engineering, 2005,27(6):616-620.

[13] 王新敏, 李义强, 许宏伟. ANSYS结构分析单元与应用[M].北京：人民交通出版社, 2011. WANG Xinmin, LI Yiqiang, XU Hongwei. The element and application of ANSYS in structral analysis[M]. Bijing: China Communications Press, 2001.

[14] Malika Azmi, Patrick P. Three dimensional analysis of concrete dams including contraction joint non-linearily [J].Engineer ing Structure,2002,24:757-771.

[15] 何玉林, 张立刚, 韩德海, 等. 风力机轮毂和轴承螺栓联接接触分析[J]. 重庆大学学报,2009,32(7):762-765,774. HE Yulin, ZHANG Ligang, HAN Dehai, et al. Contact analysis of MW wind turbine hub and bearing bolt connection[J]. Journal of Chongqing University, 2009,32(7):762-765,774.

[16] 张玉平,袁鹏,罗超云,等. 嘉绍大桥钢箱梁施工过程中局部稳定及强度分析[J]. 公路交通科技,2014,31(2):47-53. ZHANG Yuping, YUAN Peng, LUO Chaoyun et al. Analysis on local stability and strength analysis of steel box girder in construction process of Jiaxing-Shaoxing bridge[J]. Journal of Highway and Transportation Research and Development,2014,31(2):47-53.

Sensitive reserch of orbit elevation error of steel box girder slipping in the complicated track

YUAN Peng1，LI Dejian1,LU Yao1，LI Chuanxi2

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410076, China)

Based on the slipping process research of Jiashao Bridge between steel box girder and complex track in area without stayed cable under 2 types of most unfavourable condition, a FEM model, considering the contact effects between steel box girders and tracks, was established for the sensitivity analysis of structure force and deformation in various types of extreme condition by ANSYS. The standard of error control in different working conditions were discussed. The result shows that slider bearing reaction, structure deformation and stress are sensitive to restraint conditions on track bottom and track elevation error during slipping process. If track bottom has the same restraint, diagonal elevation error of track erection shouldn’t be more than 5 mm and limit value should be 8 mm. If restraint conditions are different, diagonal elevation error shouldn’t be more than 2 mm and limit value should be 4 mm. In conclusion, the stronger restraint conditions, the more sensitive vertical error of bearing reaction, the larger distribution ratio of bearing reaction and the larger increase ratio of bearing reaction, the in-plane buckling easily.

bridge engineering；complex track；sensitivity analysis；track elevation error；stress amplitude

2016-02-23

李德建(1967-)，男，湖南邵阳人，教授，从事桥梁工程教学和研究工作；E-mail: dejianli@vip.sina.com

U448.27

A

1672-7029(2016)12-2434-07