多面体的外接（内切）球半径的求法举要

张世林+谭斌

求三视图还原而成的几何体的外接（内切）球的表面积或体积的问题在2016届各地的高考模拟题中大量出现，这是高考的重点，也是学生学习的难点.困难表现在两个方面：一是根据三视图如何准确还原几何体；二是依据画出的几何体的特征如何采用适当的方法求外接（内切）球的半径.现就此类问题的常见求法举例分析如下.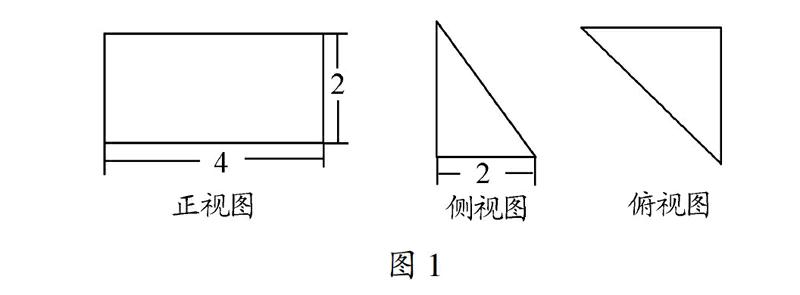

1找“墙角”

例1已知某几何体的三视图1如图所示，则该几何体的外接球的表面积为（）

图2解析如图2，还原的多面体就是三棱锥A-BCD，其外接球也是此三棱锥所在的长方体的外接球，注意：DC，DE，DF两两互相垂直，形似“墙角”，而长方体的体对角线就是其外接球的直径.故外接球的直径

2r=22+22+42=26，球的表面积S=4πr2=24π，故选C.

2寻外心

①当几何体中出现两个垂直关系，利用直角三角形斜边的中线等于斜边一半，球心为直角三角形斜边中点（即直角三角形的外心）.

②因为球心与截面圆圆心的连线垂直于截面，截面圆上的点与圆心、球心构成直角三角形，运用公式R2=r2+d2求半径.

例2已知三棱锥的四个顶点都在球O的球面上，如图3，AB⊥BC且PA=7，PB=5，PC=51，AC=10，求球O的体积.

图3解析AB⊥BC且PA=7，PB=5，PC=51，AC=10，因为72+512=102，所以知AC2=PA2+PC2，所以PA⊥PC，所以在Rt△ABC中斜边为AC，在Rt△PAC中斜边为AC，取斜边的中点O，在Rt△ABC中，OA=OB=OC，在Rt△PAC中，OP=OB=OC，所以在几何体中OP=OB=OC=OA，即O为该四面体的外接球的球心，R=12AC=5，所以该外接球的体积为V=43πR3=500π3.

例3已知三棱锥S-ABC所在顶点都在O的球面上，且SC⊥平面ABC，若SC=AB=AC=1，∠BAC=120°，则球O的表面积为.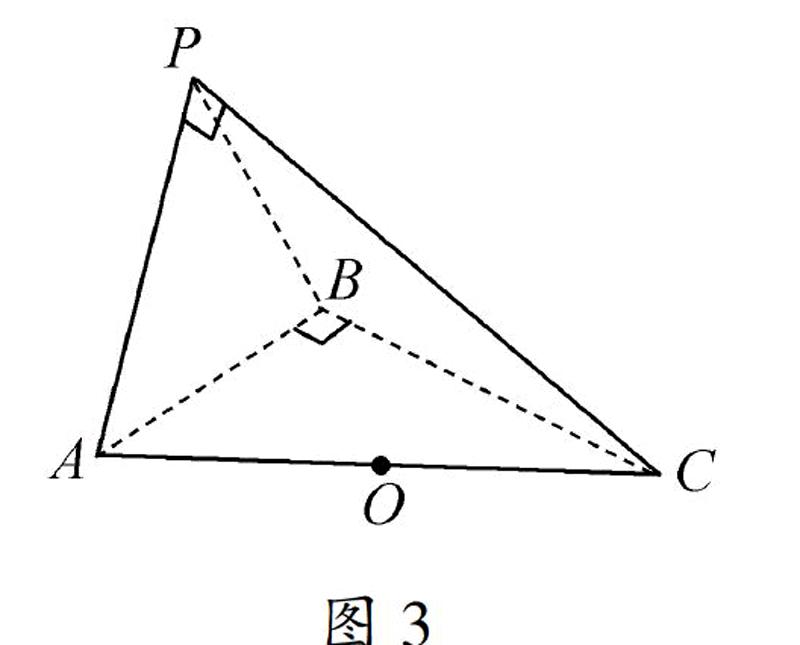

图4解析如图4，以底面三角形ABC的边AB，AC为邻边作菱形ABDC，再作OD⊥平面ABC，又因为SC⊥平面ABC，所以OD∥SC，过点D作DE⊥SC，垂足为E，在直角梯形ODCS中，OC=OS=r，所以可得OD=12，所以r=OD2+OE2=122+1=52，则球的表面积为S=4πr2=4×π×522=5π，故应填5π.

变式：一几何体的三视图如图5，则它的外接球的表面积为（ ）

图5A. 12πB. 16πC.20πD. 24π

图6解析如图6，还原的多面体就是三棱锥P-ABC，AB⊥BC，面PBC⊥面ABC，∠PBC=120°，AB=AC=2，先找出△ABC的外心即斜边AC的中点I，设球心为O，连结OA，OI，OP，显然OI⊥平面ABC，过点P作PE⊥BC交BC于E，连结IE，那么PE∥OI，过球心O作OF∥IE交PE于F，显然四边形OIEF为矩形，设OI=h，OA，OP为球半径r，EB=2cos 60°=1，PE=3，在△CEI中由余弦定理易得EI=5，因为h2+22=52+3-h2，得h=3，从而r=5，S=20π，故选C.

3作截面

通过寻找外接球的一个轴截面圆，把立体几何问题转化为平面几何问题来研究.

例3已知一几何体的三视图如图4所示，则此几何体的外接球的体积为.

图4图5解析由三视图易得，几何体为如图5所示的正四棱锥，设正四棱锥的底面中心为O1，外接球的球心为O，如图所示，由球的截面性质，可得O1O⊥平面ABCD，又SO1⊥平面ABCD，所以球心O必在SO1所在的直线上，所以△ASC的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径，在△ASC中，由SA=SC=2，AC=2，得SA2+SC2=AC2，即SA⊥SC，所以AC是△ASC的外接圆的直径，即为外接球的直径，故V=43π.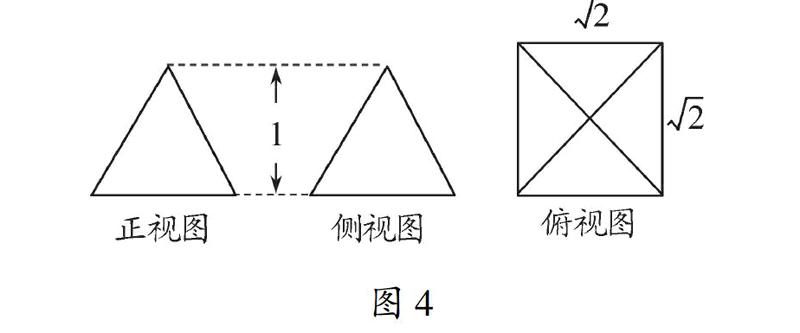

4用结论

正四面体的外接球与内切球的球心重合于正四面体的高线上一点，外接球与内切球的半径之和等于正四面体的高，外接球的半径等于内切球半径的3倍，外接球的半径等于正四面体棱长的64，内切球的半径等于正四面体棱长的612.

例4如图6所示为某几何体形状的纸盒的三视图，在此纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动，则小正四面体的棱长的最大值为（）

A.33B.13C.24D.324

解析显然由三视图还原而成的纸盒是棱长为3的正四面体，利用上述结论可得纸盒的内切球半径为24，要使小正四面体在纸盒内可以任意转动，要求小正四面体棱长的最大值，即小正四面体的外接球就是纸盒的内切球.易得小正四面体的棱长的最大值为33，故选A.

图71.如图7，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体外接球的表面积为.

2.在四面体ABCD中，共顶点的三条棱两两垂直，其长度分别为1，6，3，若该四面体的四个顶点在一个球面上，求这个球的表面积.

3.如图8是某几何体的三视图，则该几何体的体积为（）

A.83 B.43C.823 D.423

4.如图9，网格纸上小正方形的边长为2，粗线画出的是某几何体的三视图，则该几何体的体积是（ ）

A.6πB.7π C.12πD.14π

如图10，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（ ）

A.8π B.252π C.12πD.414π

答案1.41π；2.S=4πR2=16π；3.A；

4.D；5.D