递推法在概率论解题中的应用分析
江苏省张家港市张家港开放大学 陈海文
递推法在概率论解题中的应用分析
江苏省张家港市张家港开放大学 陈海文
新课改背景下,概率成为高中数学教学的新内容,鉴于概率具有重要的理论性和实际性,在教学中占据重要位置。特别是在近年的高考中,有关概率、组合、排列的问题不断增多并且问题类型不断翻新。任何问题的解决,其方法非常重要,所以针对概率论解题中递进法的实际运用进行分析,探究高效的解题方法,对于教学质量以及学习效率的提高具有积极的推动作用。本文就概率论、递推法等概念进行分析,结合实际问题研究递推法在概率论问题解决过程中的实际应用,以期为相关问题的解决提供帮助。
递推法;概率论;应用
在一些概率问题解决的过程中数学思想的方法得到了充分应用,成为知识与能力之间转换的桥梁,提高数学思想在概率解题过程中的正确运用的思想认识,同时也反映出学生学习的水平及解题能力。在数学诸多的思想方法中,递推法在各个学科领域的应用比较广泛。尤其是近年来,递推法在概率类解题中的渗透成为教学的重点,同时也是新课标与高考的基本要求,因此分析研究概率解题中递推法的实际应用,应当引起教师及学生的高度重视,更是提高解题能力与解题质量的重要手段。
一、定义解析
1.递推法的含义
递推法是以具体问题为根据,进行递推关系的构建,然后利用递推关系实现问题的求解,是将若干个可重复的简单运算应用到对复杂问题进行描述的一种方法。其中有关正整数的参变量特殊关系可通过递推关系来表示,这是个以指定的初值为出发点,然后运用递推关系进行逐步计算,最终获得需要的结果。计算机序列运算中,递推法是比较常用的一种方法。序列当中的每项的计算都是利用一定规律来实施,指定项的值是通过对位于计算机前面的项的运算得出。将庞大、复杂的计算过程变得简单化的重复运算,这种方法将计算机可无限运作与快速的优势充分发挥出来。
递推法的解题过程一般包括:按照次序对集合中的最原始、最初若干问题进行研究;按照次序对集合中存在问题之间互为转换的规律,也就是推进关系进行探寻,最终逐次转化问题为简单的、底层的,并且能够解决或者已经解决的问题。
2.概率的含义
对于随机现象的数量规律进行研究的一个数学分支称为概率。这里的随机现象泛指决定现象相对而言。而决定性现象是指一定条件下,一种结果将会必然产生的现象。比如,标准气压下,当纯水温度上升至100℃时,必然会出现沸腾现象。随机现象通常指基本条件确定的状况下,每次的观察与实验前,对于哪种现象的发展不能肯定,具有很大的偶然性。在随机试验中,事件的发生虽然具有偶然性,但是相同条件下的反复进行的大量随机试验所呈现出来的数字规律往往是非常明显的。
概率思想不仅在学科教育方面应用比较广泛,同时在其他领域也得到了部分应用。在学科教育方面,概率思想主要组成部分有计算以及证明,其中举例论证以及递推解题法的应用比较广泛,将解题过程中不能简单、快捷解决的问题,在概率解题思想的引导下,能够使计算步骤得到简化,计算次数大幅减少,节约解题时间,同时又使计算或者证明的准确性得到保障,使学生的基础知识得到巩固,解题的实际能力大大提高。
二、递推法在概率论解题中的实际应用
通过初始值的递推,继而获取必要的结果。对于离散样本,尤其是古典的概率类型的问题,都是些针对有关于自然数的事件概率而进行的研究。目前,在中小学教学阶段,有关自然数的概率问题的解决,很好地运用到了递推解题方法,能够充分体现出递推法解题具有很好简洁性,其中有些问题唯有适合用递推法给予解决。
例题一:对于有N个点组成的任意一个网络图,其中的任意一点都相连于N-1个点,从任意点A开始出发,在等概情况下,每次选择一条途径达到另一点,经过f步后返回A点的概率是多少?
方法一:从A点开始走f步共有(N-1)f次不同的路径,假设返回A点的路径有af条,那么从A点开始走f-1步的路径有(N-1)f-1条,回到A点的路径有(a)f-1条,剩下的每种在向前走一步的情况下即可到达点A,因此,则。
由此可以得出从A点出发,经过f步后返回A点的概率为
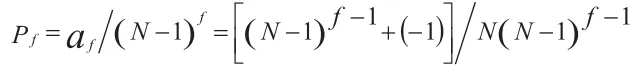
方法二:假设由A点开始经过f以后返回A点的概率为Pf,则,P0=1,P1=0,第f-1步没有在A点上,在另外的N-1个任意点有的概率,由第f步返回A点有,则

以上两种解题方法均为递推法。
例题二:将一枚硬币在连续投掷n次后,求在硬币投掷过程中,出现两次连续正面向上的概率为多少?
解题思路;针对这样的问题,如果采取直接下手解决,难度比较大。这种情况下可采用间接的解题方法进行思考,把不发生连续两次正面向上的概率设定为0,以此为突破口寻找问题解决的途径。
将不发生连续两次正面向上的概率设定为Pn,那么,当P1=1时,P2=3/4,如果n大于2,则会有以下两种情形产生。
第一,如果第一次投掷时是背面向上,那么在以后的n-1次投掷过程中,将会有Pn-1的概率不发生连续两次投掷正面向上。
第二,如果第一次投掷时是正面向上,为了避免连续两次投掷正面向上的情况发生,则第二次投掷则必须是反面向上,剩下的n-2次投掷将会有Pn-2的概率不发生连续两次正面向上。
例题三:甲、乙两人玩掷骰子游戏,游戏要求为:当所投掷的骰子点数是3的倍数,掷骰子的一方可以继续投掷;如果所投掷的骰子点数非3的倍数,则由另一人开始投掷,假如第一次甲开始投掷,求在第n次时仍旧由甲投掷的概率为多少?
连续两次投掷骰子,其点数的和是3的倍数时,其概率P值是12/36=1/3,在点数和不是3的倍数时的概率是1-1/3=2/3,就针对第n次投掷由甲来操作,其中包括甲投掷的第n-1次投掷。而甲继续在第n次投掷以及乙投掷第n-1次,甲投掷第n-1次这一事件,两个事件的关系是相互驳斥的,甲投掷第n次的概率是Pn-1,乙投掷概率则是1-Pn-1,因此,……显而易见,P1=1,由上面的式子可得,因此,,进而可得,(n≥1,且n≤N)。
总之,递推法在概率论教学实践中的应用地位非常重要,由上述例子的解题过程不难看出,推进法能够将概率论思想刻画地更加直观,实现概率问题和直观解题之间互为转化,实现抽象与形象思维的有效融合;递推法的应用,使数量关系与空间的实际形式进行结合,来寻找、创新心的解题思路,确保问题的顺利解决。只有对概率课的特性进行充分把握,有效实施递推教学方法,最终促进教学效率,提高学生高效学习的效果。
[1]刘建波.“递推思想”在数学解题中的应用举例[J].科学咨询:教育科研,2010(4).
[2]刘国军.“递推法”在解答高中物理试题中的运用[J].中学物理:高中版,2015(11):72-73.
[3]沈春林.递推思想在概率问题中的有趣应用[J].数学通讯,2013(10).

