一题多解，挖掘问题的本质——彰显数学的魅力

西安交通大学附属中学分校 熊 敏

一题多解，挖掘问题的本质
——彰显数学的魅力

西安交通大学附属中学分校 熊 敏

我们在中考复习的过程中，教师常常会引导学生一题多解。笔者认为作为教师要让学生有展示的机会，并且要对学生的不同解法做出有层次的评价，挖掘出问题的本质，这样对学生学习能力的发展能起到很好的推动作用。下面，我要从一道中考真题的一题多解谈谈如何进行一题多解教学。

2013年陕西中考第10题：

已知两点A（－5，y1）、B（3，y2）均在抛物线y=ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点，若y1＞y2≥y0，则x0的取值范围是（）

A.x0＞－5 B.x0＞－1 C.－5＜x0＜－1 D.－2＜x0＜3

生甲：老师，我的解法是：

将A（－5，y1）、B（3，y2）代入y=ax2+bx+c（a≠0）得，

生乙：老师，我在甲同学的方法的基础上稍有改动，我的解法是：

由y1＞y2得：25a-5b+c＞9a+3b+c，

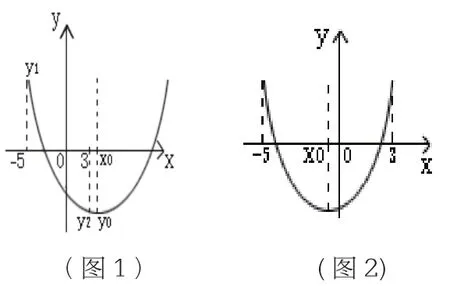
生丙：老师，我与前面两位同学的方法完全不同，不用计算，只要画图像就可以得到答案。

由y1＞y2≥y0得a＞0。

（1）当A、B在对称轴的同侧，如图1，则x0≥-3，（2）当A、B在对称轴的异侧，如图2，假设y1=y2，则x0=-1，但y1＞y2，∴-1＜x0＜3，综上x0＞-1。

生丁：老师，我在丙的基础上，不用分情况也能说理清楚：

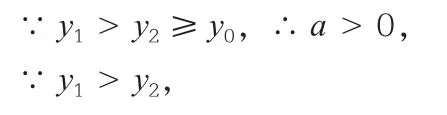
两边平方，化简得x0＞-1。

教师点评：

甲、乙两生是同一种方法，均为代数方法，在解y1＞y2不等式的过程中，甲生用到了代入消元的思想，减少参数的个数才使得x0的范围柳暗花明；乙生用到了分析法，要求x的范围，只要求-

0的范围即可，从结论出发找原因，是今后我们分析问题常用的方法。

丙生用了图像法，非常形象直观的帮助我们找到了x0的范围，但同学们应用这种方法时容易忽视二次函数有两段单调区间，忘记分类讨论，以偏概全。这也是出题人抓住了考生的心理，设下的陷阱。

丁生的解法由于抓住了比较二次函数两个函数值大小的本质，二次函数的增减性由开口方向和对称轴共同确定，由题可知，抛物线开口向上，A、B两点谁离对称轴近谁对应的函数值就小。

同学们在经历了与甲、乙两位同学的代数方法的比较，与丙生分类讨论，图像法的铺垫，一致认为，我们在解决此类问题时，丁生把数与形结合起来的方法，更为简洁易懂。所以，让学生在比较、讨论、争论中，找出最简便的解法和独特的富有新意的解题思路，有利于加深学生对多种解题方法的认识，从而更熟练地把握一类题目的解决方法。

引导学生自己找出最简便的解法，在学生求得多种解题方法之后，让他们自己去分析比较，可以相互讨论，在分析比较、相互讨论的过程中感受最简便的解题方法。这一过程就是一个继续思考的过程，也是对一类题的各种解法的再认识的过程。只有经历了这样的过程，才能真正把握一类题的最简便的解题方法，才能进一步提高解决问题的能力和效率。