双差/非差解算模式对定位精度的影响分析

吴 波 ，党亚民，杨 强，宋传峰，王丹萍

(1.江苏省测绘工程院，江苏 南京 210013；2.中国测绘科学研究院，北京 100830；3.江苏省苏测信息科技有限公司，江苏 南京 21111)



双差/非差解算模式对定位精度的影响分析

吴 波1，党亚民2，杨 强2，宋传峰2，王丹萍3

(1.江苏省测绘工程院，江苏 南京 210013；2.中国测绘科学研究院，北京 100830；3.江苏省苏测信息科技有限公司，江苏 南京 21111)

针对目前高精度数据处理中双差网解与非差PPP解2种解算模式间精度差异的问题，进行了相同的观测数据在上述2种解算模式下的定位精度分析：首先分别阐述了双差非差数学模型，然后使用地中海周边若干IGS站观测数据进行实验。结果表明：双差、非差解坐标分量差值在1～2 cm左右；双差、非差解算模式下，基线较短时基线长度差异较小，最大约为1 cm；随着基线长度的增加，基线长度差异表现出明显的累积性；综合比较坐标分量和基线长度差异可知，双差解算模式适用于精度要求较高的国家CORS网数据处理，非差处理模式适用于精度相对较低的省级CORS站框架维护。

双差模式；非差模式；定位精度；基线

0 引言

高频全球定位系统(global positioning system，GPS)数据处理方法主要有双差和非差2种模式[1]。数据处理时在载波相位观测值一次求差的基础上继续求差所获得的虚拟观测值结果，称为双差。双差观测消去了卫星钟差和接收机相对钟差的影响。此外在站点相距不远的情况下，双差可消除大多数电离层和对流层效应[2]。双差处理模式是目前全球卫星导航系统(global navigation satellite system，GNSS)数据处理中的主流方式。

非差处理模式目前典型的应用是精密单点定位(precise point positioning，PPP)技术。利用国际GNSS服务(international GNSS service，IGS)提供的卫星精密轨道和钟差产品，外加一台GPS双频接收机即可解算出测站三维坐标、接收机钟差、卫星钟差、电离层和对流层延迟改正信息等参数。PPP模式采用单站进行作业，具有定位方式灵活、各测站的解算相互独立、不受基线长度影响、解算速度快的优点[3]。

已有文献[4-5]得出网解和非差解等价的结论；但对于对点位精度有严格要求的国家基准高精度框架维护，非差解算模式的精度能否达到与双差解算模式同等精度水平则一直引人关注。本文采用实测数据在双差和非差模式下进行解算，量化2种解算模式之间解算精度的差异。

1 双差和非差模型比较

GPS精密定位从观测值角度可分为非差定位模式和双差定位模式，本节从误差源角度给出2种定位模式的具体优势。

1.1 双差模型

载波相位双差数学模型由图1可得，测站1、2对卫星j、k的载波相位观测方程[6]为

(1)

图1 相对定位图示

在测站间求单差，再在卫星间求双差，即可得出双差观测方程为

ΔNk。

(2)

式中：

Δφk(t)=Δφk(t)-Δφj(t)；

(3)

ΔNk=ΔNk-ΔNj；

(4)

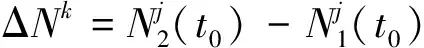
(5)

其中：Δφk(t)表示测站间的载波相位观测量之差；ΔNk表示2测站观测同一颗卫星整周模糊度差值。

从双差观测方程可以看出：双差最重要的特点是完全消除了卫星钟差和接收机钟差的影响。此外，双差可消除大多数电离层和对流层效应，特别是测站之间距离不远的情况[2，7]。

1.2 非差模型

PPP采用双频观测值进行定位时，通常采用无电离层组合观测值，其基本观测方程[8-9]为：

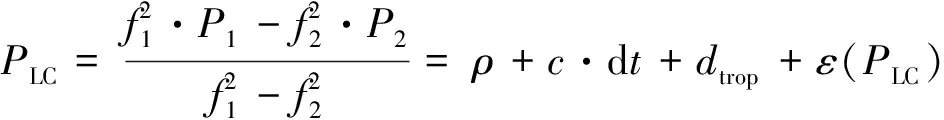
(6)

dtrop+Nλ+ε(ΦLC)。

(7)

式中：Pi为伪距观测值；Φi为载波相位观测值；dt为接收机钟差；dtrop为天定对流层延迟；fi为载波Li频率；N为无电离层组合模糊度；ε为随机噪声和多路径误差；ρ为卫星和接收机之间的几何距离即

(8)

在精密单点定位中使用非差观测值，没有组成差分而是采用精密星历消除卫星轨道误差项；利用卫星精密钟差估计值消去卫星钟差项；采用双频观载波测值消除了电离层一阶项的影响，忽略电离层高阶项的影响；采用Hopfield模型、Saastamonien模型，NMF、CMF投影函数进行对流层延迟改正；采用IGS发布的卫星和接收机天线相位中心改正模型进行天线相位中心偏差改正；将接收机钟差作为一个未知参数进行估计，与其他参数一起解算；通常情况下，非差精密定位数学模型中，多路径误差没有采用模型进行改正，也没有作为未知数进行估计，因此定位结果中会包含多路径误差的影响[7]。

2 双差网解和非差PPP解的结果比较

为了比较双差解和非差解实际结果的差异，综合考虑短(<50 km)、中(50～200 km)、长(>200 km) 3种基线类型，选取地中海沿岸7个IGS站作为待求站，全球均匀选取52个IGS核心站作为公共起算站，站点分布见图2。公共站的坐标采用强约束，其他站完全放松。待求站数据处理分别采用GAMIT/GLOBK软件和BERNESE软件进行：GAMIT软件是目前非常具有代表性的采用双差模式的高精度数据处理软件；BERNESE软件包含了PPP解功能，对应采用非差解算模式。采用GAMIT软件进行解算时，解算策略的主要参数设置如表1所示[10]，其他参数采用默认值。PPP的计算利用IGS发布的精密钟差和最终轨道，连续地处理所有待求IGS站的数据；数据处理的基本设置如同GAMIT软件，站坐标参数完全放松。从站点坐标分量和基线长2方面对实验结果进行比较。

图2 基准站及待求站分布图

处理参数设置处理参数设置处理模式RELAX潮汐改正不使用观测值的选取LC⁃HELP约束站ARTU等对流层误差模型SAASTAMONIEN其他100100100光压模型BERNE固定坐标参考框架ITRF2005数据筛选AUTCLN截止高度角10°大地水准面模型EGM96采样间隔30s

2.1 站坐标绝对值比较

本文选取了2013年年积日328～334连续7 d的观测数据，图3显示了部分待求站双差解和非差解的坐标值在X、Y、Z方向的差值。根据坐标分量的残差量级可以发现，双差和非差解差异在2 cm以内，在实际数据处理中，不能得出双差解与非差解完全等价的结论。

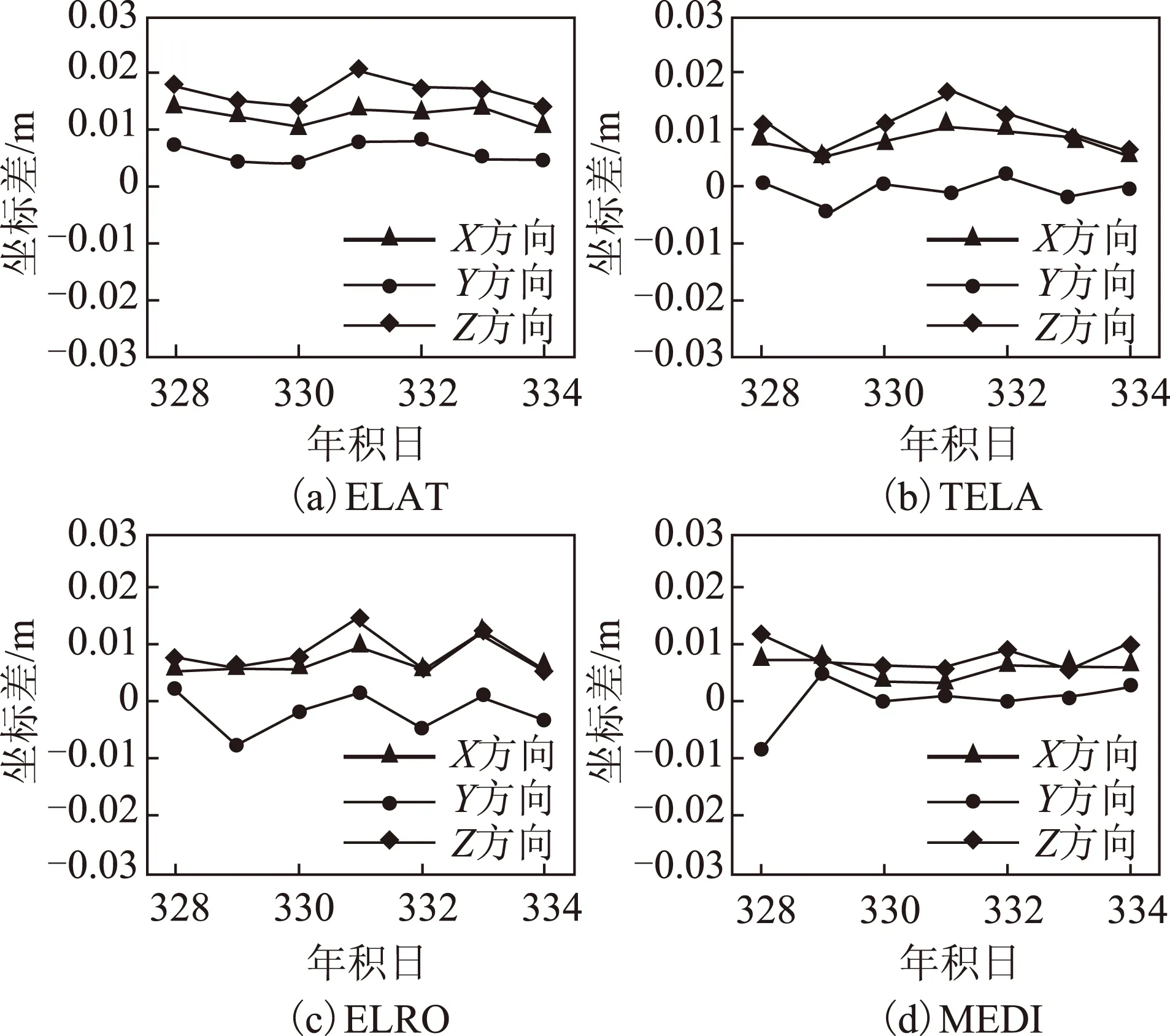
图3 双差解和非差解的坐标值比较

2.2 不同模式下基线长度的比较

除坐标外，还比较了2种解算模式下基线长度之间的差异。将经GLOBK平差后站点坐标作为参考值计算所有基线长度，分别与2种解算模式下对应基线长度进行比较，具体差异数值见表2，对应的差值分布如图4所示。可以发现：非差解算模式下基线长度变化较大；双差解算模式下基线长度变化较小。当基线较短时，种解算模式下基线长度相差较小，最大约为1 cm。随着基线长度的增加，2种解算模式下基线长度的差异越发明显。

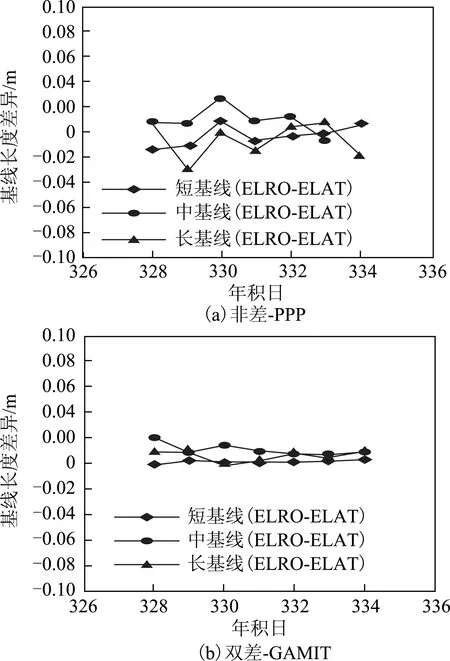
图4 双差解和非差解对应不同基线长度比较

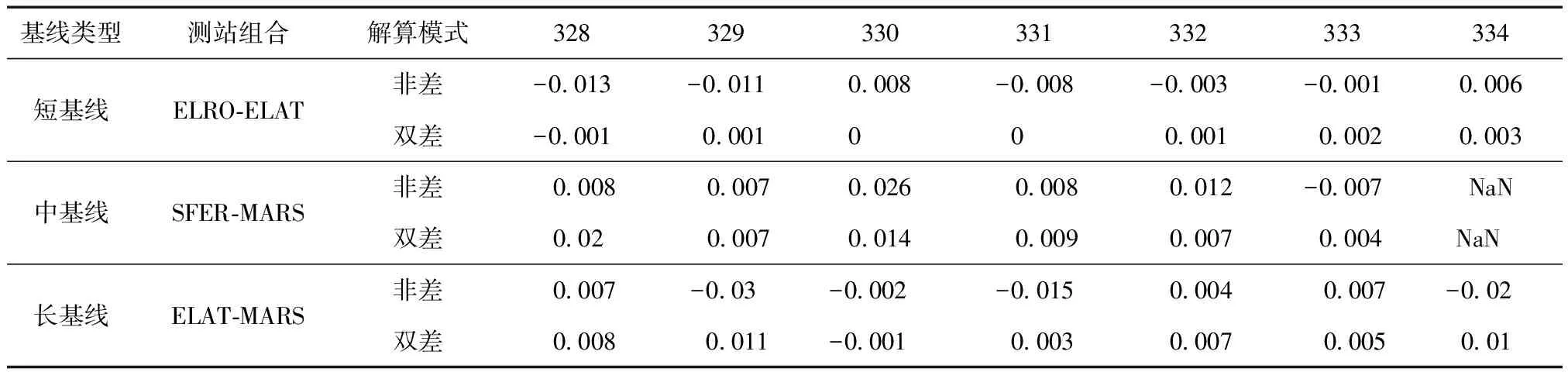
表2 双差解和非差解对应基线差异数值 m

注：“NaN”表示由于SFER站年积日334 d没有数据。

3 结束语

双差解和非差PPP解是当前GPS数据处理中的2种方式。本文通过随机选取的7个IGS站在2种解算模式下2013年年积日328～334共7 d的坐标分量，经计算、分析得出以下结论：

1)双差、非差单天解坐标分量的差值在2 cm以内。

2)非差解算模式下计算得出的基线长度变化较大，而双差解算模式下得出的基线长度变化平稳。

3)基线较短时，双差、非差解算模式下，基线长度差异较小，最大约为1 cm。

4)随着基线长度的增加，基线长度的差异表现出明显的累积性。

对于解算精度要求达到mm级的国家连续运行参考站(continuously operating reference stations，CORS)系统网数据处理，双差解以其解算精度高的优越性成为其数据处理的主流手段。而对于精度要求在1～2 cm的省级CORS站框架维护，非差解算模式能够快速完成数据处理，并能够满足解算精度，因而成为其数据处理的首选。

[1] 吴继忠，吴文坛.利用高频GPS进行地震动态变形分析及地震定位[J].大地测量与地球动力学，2012，32(2)：20-23.

[2] 许国昌.GPS理论、算法与应用[M].李强，刘广军，于海亮，等译.2版.北京：清华大学出版社，2011：151-151.

[3] 党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用[M].北京：测绘出版社，2007：78-79.

[4] 刘焱雄，彭琳，周兴华，等.网解和PPP解的等价性[J].武汉大学学报·信息科学版，2005，30(8)：736-738.

[5] 韩保民，欧吉坤.基于GPS非差观测值进行精密单点定位研究[J].武汉大学学报·信息科学版，2003，28(4)：409-412.

[6] 王俪霏，李博峰，张兴福.北斗与GPS随机模型对比分析[J].测绘工程，2014，23(10)：9-13.

[7] 崔阳.大规模测量平差分布式计算技术及应用研究[D].郑州：信息工程大学，2013： 63-64.

[8] 方荣新，施闯.高采样率GPS数据非差精密处理方法及其在地震学中的应用研究[D].武汉：武汉大学，2010：30-32.

[9] 辜声峰.多频GNSS非差非组合精密数据处理理论及其应用[D].武汉：武汉大学，2013：138-140.

[10]王超，郭际明，周命端，等.高精度GPS数据处理中GAMIT批处理方法与实现[J].测绘信息与工程，2012，37(2)：10-12.

Influence analysis of double differential and un-differential calculating mode on positioning accuracy

WU Bo1，DANG Yamin2，YANG Qiang2，SONG Chuanfeng2，WANG Danping3

(1.Jiangsu Province Surveying & Mapping Engineering Institute，Nanjing，Jiangsu 210013，China;2.Chinese Academy of Surveying and Mapping，Beijing 100830，China;3.Jiangsu Province Suce Information Technology Co.，Ltd，Nanjing，Jiangsu 211111，China)

Aiming at the problem of the precision difference between double differential network solution mode and un-differential PPP solution mode in high precision data processing，the paper analyzed the positioning accuracy of the same observation data with above-mentioned two modes：the mathematical models of the two modes were elaborated，and an experiment was conducted by using the data of IGS stations around Mediterranean Sea finally.Result showed that the coordinate component difference between the two modes would be about 1～2 cm；when the baseline was short，the baseline length difference in above two modes would be small，the biggest could be about 1 cm，and with the increase of baseline length，the length of baseline differences would show obvious cumulativity；through synthetically comparing between the coordinate components and the baseline length difference，it could be indicated that double differential mode would apply to national CORS net data processing under requirement of high precision，while undifferential mode would be suitable for provincial CORS framework maintenance with the requirement of comparatively low precision.

double differential mode；un-differential mode；location accuracy；baseline

2015-07-30

国家自然科学基金项目(41474011)；中国测绘科学研究院科研业务费支持项目(7771502，7771405)。

吴波(1989—)，男，江苏盐城人，硕士研究生，研究方向为高精度GNSS数据处理。

吴波，党亚民，杨强，等.双差/非差解算模式对定位精度的影响分析[J].导航定位学报，2016，4(4)：100-103 .(WU Bo，DANG Yaming，YANG Qiang，et al.Influence analysis of double differential and un-differential calculating mode on positioning accuracy[J].Journal of Navigation and Positioning，2016，4(4)：100-103.)

10.16547/j.cnki.10-1096.20160419.

P228

A

2095-4999(2016)04-0100-04