BDS/GPS观测噪声对模糊度解算的影响分析

邱晓璐，刘根友

(1.烟台黄金职业学院，山东 招远 265400；2.中国科学院 测量与地球物理研究所，湖北 武汉 430077)



BDS/GPS观测噪声对模糊度解算的影响分析

邱晓璐1，刘根友2

(1.烟台黄金职业学院，山东 招远 265400；2.中国科学院 测量与地球物理研究所，湖北 武汉 430077)

针对观测噪声会影响模糊度正确解算的问题，提出采用观测数值仿真，从模糊度解算的正确性和模糊度识别的有效性2方面来分析BDS和GPS不同观测噪声对模糊度解算的影响。利用非差观测模型与双差观测模型的一致性，忽略电离层延迟及对流层延迟误差，选取中国大陆具有区域代表性的8个观测站进行实验，结果表明：无论从模糊度解算的正确性还是模糊度识别的有效性分析，BDS在各地区观测时长为30 min时模糊度能成功固定的最大观测噪声与GPS观测时长为5 min时相当，即与GPS相比，BDS的观测噪声较大、观测时间较短时，载波相位定位的模糊度很难成功固定。

BDS；GPS；载波相位定位；观测噪声；整周模糊度

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)一般具有伪距和载波相位2种观测量。载波相位定位技术能够实现cm甚至mm级高精度定位，但其先决条件是正确解算出整周模糊度。高精度载波相位定位在民用以及军事方面都有着广阔的应用前景，广泛地应用于大地测量、地球动力学以及精密工程测量等各个方面[1-5]。目前模糊度解算一般采用的是整数最小二乘法，通过参数浮点解、整周模糊度搜索和固定解3个步骤实现[6]。国内外学者对整周模糊度固定的方法进行了大量的研究并取得了很多成果，其中Teunissen提出并扩展了最小二乘模糊度降相关平差法(least-squares ambiguity decorrelation adjustment，LAMBDA)方法[7-9]，是目前最有效的模糊度搜索方法之一。

由于模糊度参数的存在，观测方程普遍存在病态性[10-11]，观测量间具有较强的相关性，用最小二乘法估计未知数的法方程严重病态，法方程的求逆不稳定；观测中观测值噪声不可避免，导致模糊度的浮点解与准确值的偏差较大，方差-协方差阵条件数太大：这种情况下难以正确获得模糊度的整数解。载波相位观测方程的病态性和观测值噪声都会影响整周模糊度的解算：文献[12]在我国不同地区不同时段对北斗卫星导航系统(BeiDou navigation satellite system，BDS)及全球定位系统(global positioning system，GPS)载波相位定位的病态性进行了对比分析；文献[13]从GPS以及BDS中不同的卫星轨道高度和运行角速度出发，采用条件数法对其不同长度基线解算中的病态性进行了对比研究；文献[14]基于不同轨道高度的卫星运行角速度不同，对比分析了BDS、GPS及其组合导航系统的病态性，得出BDS病态性较GPS严重，而组合导航系统会有很大的改善的结论。很多学者已从不同的角度对比分析了BDS和GPS系统的病态性；然而影响解算结果的最根本原因还是观测误差，如果没有误差，即使观测方程是病态的也能获得正确解。与其他平差方法的病态问题不同，BDS/GPS观测方程中的模糊度未知数具有整数特性，一旦模糊度固定，病态问题将不再存在。

本文主要分析观测噪声对整周模糊度固定的影响。模糊度解算是载波相位定位的关键，在病态程度一定的情况下，噪声越大，获得模糊度正确解的可靠性也会降低；检验模糊度整数解是否正确也是模糊度解算的关键内容之一[15-16]，因为整数最小二乘搜索总会得到一个整数解，但这一整数解是否正确需要判定。因此需要2个步骤：首先必须获得正确的整数值；其次是判定解是否正确。本文选取中国大陆具有地域代表性的8个地面站，采用仿真观测数据，从模糊度解算的正确性检验和模糊度识别的有效性2方面来分析BDS和GPS不同观测噪声对模糊度解算的影响。

1 差分GNSS与非差定位的一致性分析

高精度载波相位定位一般采用差分定位实现，差分定位的效果与基线长短有关。本文从观测模型出发，证明差分GNSS与非差定位是一致的，基线的长短仅表现为观测噪声的BDS与GPS系统的伪距和载波相位观测模型相同。测站r对卫星i的伪距和载波相位观测模型可以表示为：

cδti-dion+dtrop+εφ；

(1)

dion+dtrop+εR。

(2)

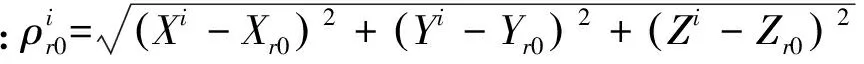
双差最重要的特点是完全消除了上述方程中的卫星轨道误差和钟差项；当测量基线较短时，对流层延迟、电离层延迟可以忽略不计[17-18]，简化的双差模型为：

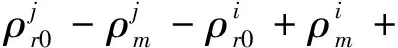
(3)

ΔεR。

(4)

2 BDS/GPS观测噪声对模糊度解算的影响分析

本文选取了我国8个具有代表性的地面站，分别是长春、乌鲁木齐、北京、西安、上海、武汉、拉萨以及昆明，各地面站的坐标采用WGS-84坐标系，地面站的坐标如表1所示。仿真了BDS和GPS 2个系统在我国8个地面站连续5 h(5∶00—10∶00)的观测数据，观测噪声为2 mm ～ 5 cm。从模糊度解算的正确性和模糊度解算识别的有效性2方面对比分析了BDS和GPS观测时长分别为5、30 min和1、2、5 h时不同观测噪声对整周模糊度解算的影响。

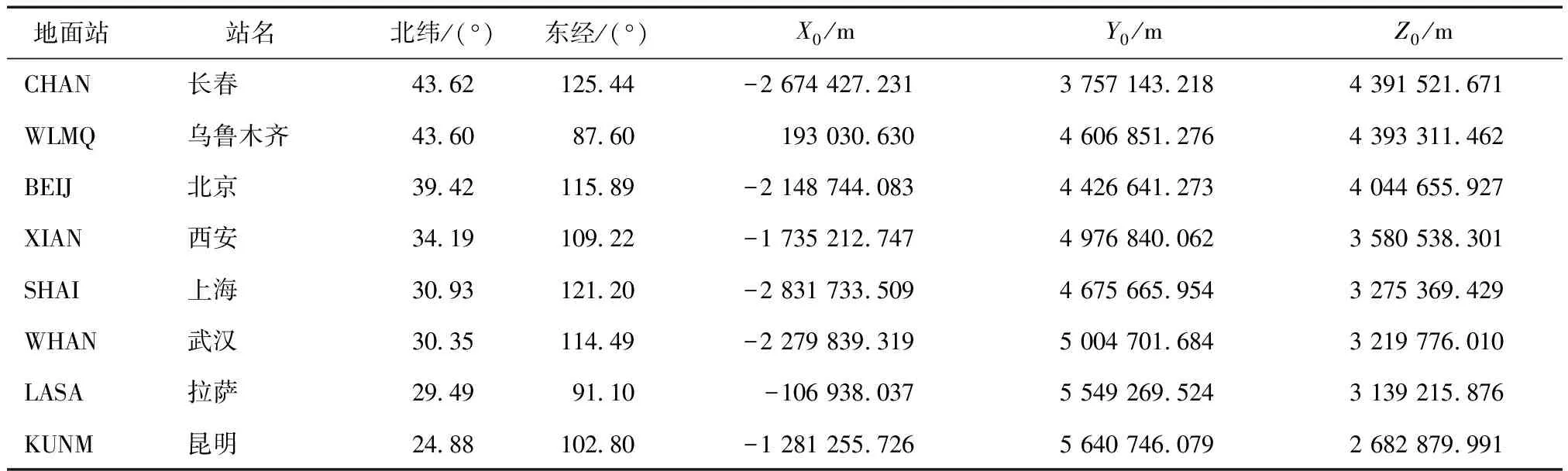
表1 地面站坐标

2.1 BDS/GPS整周模糊度解算的正确性检验

由于本文中的数据是仿真数据，在仿真观测数据时模糊度是已知的；因此整周模糊度解算值可以与已知的模糊度进行对比，首先考察整周模糊度的解算值是否正确。表2、表3列出了BDS和GPS 2个系统不同的观测噪声对整周模糊度固定的影响结果，数值1代表模糊度值正确，0代表模糊度值不正确。

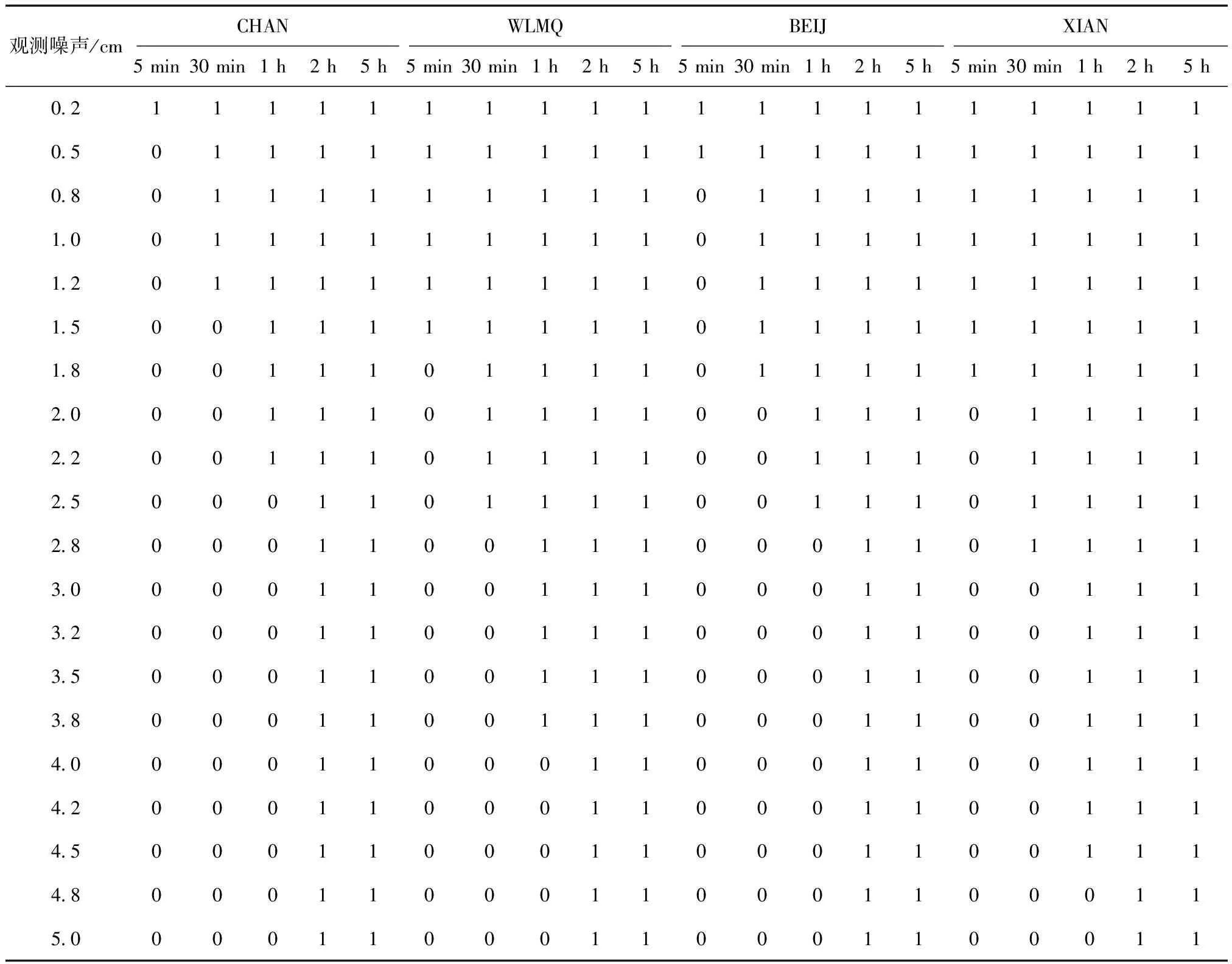
表2 BDS观测噪声对整周模糊度固定的影响

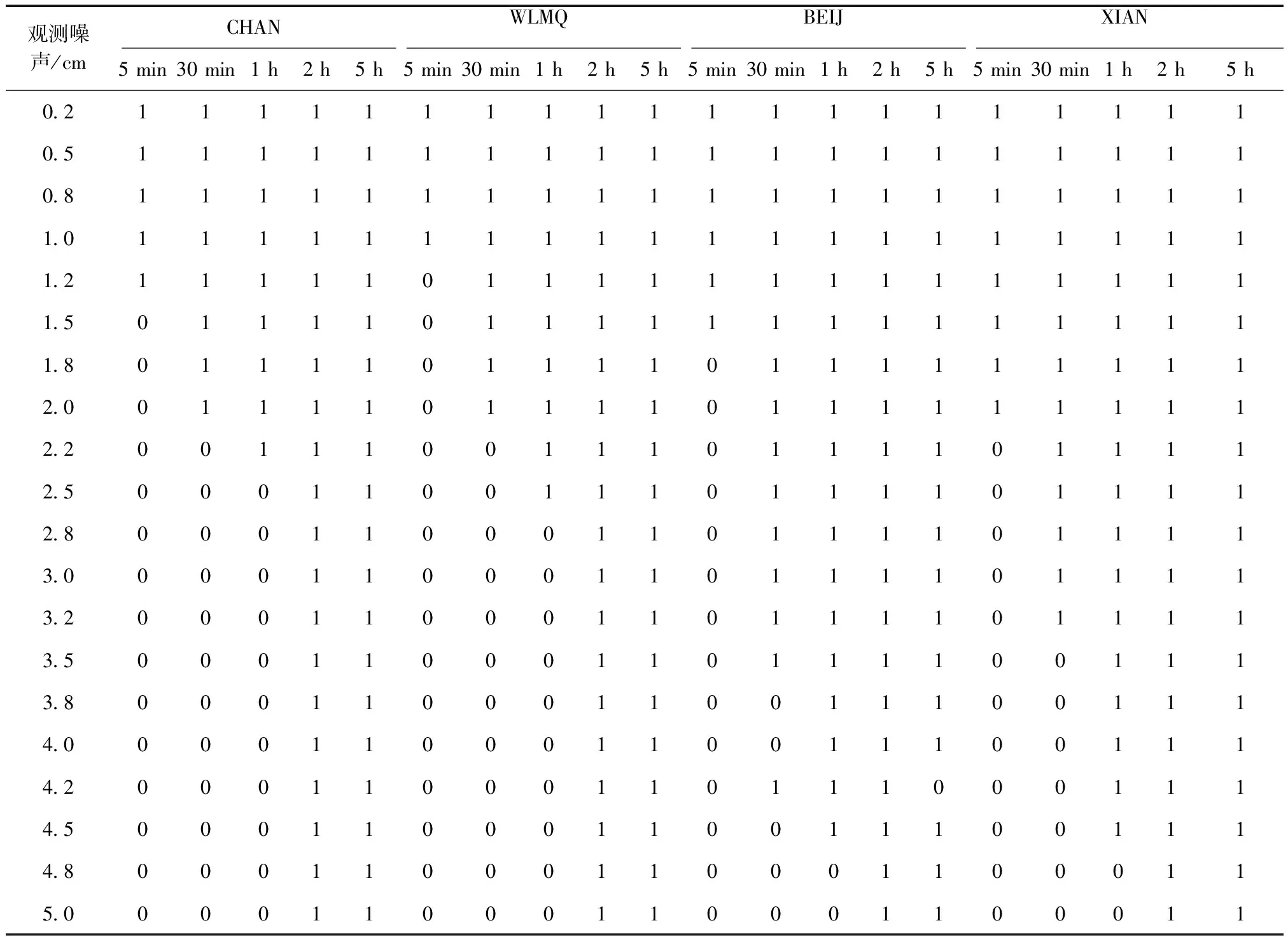
表2 续表

表3 GPS观测噪声对整周模糊度固定的影响

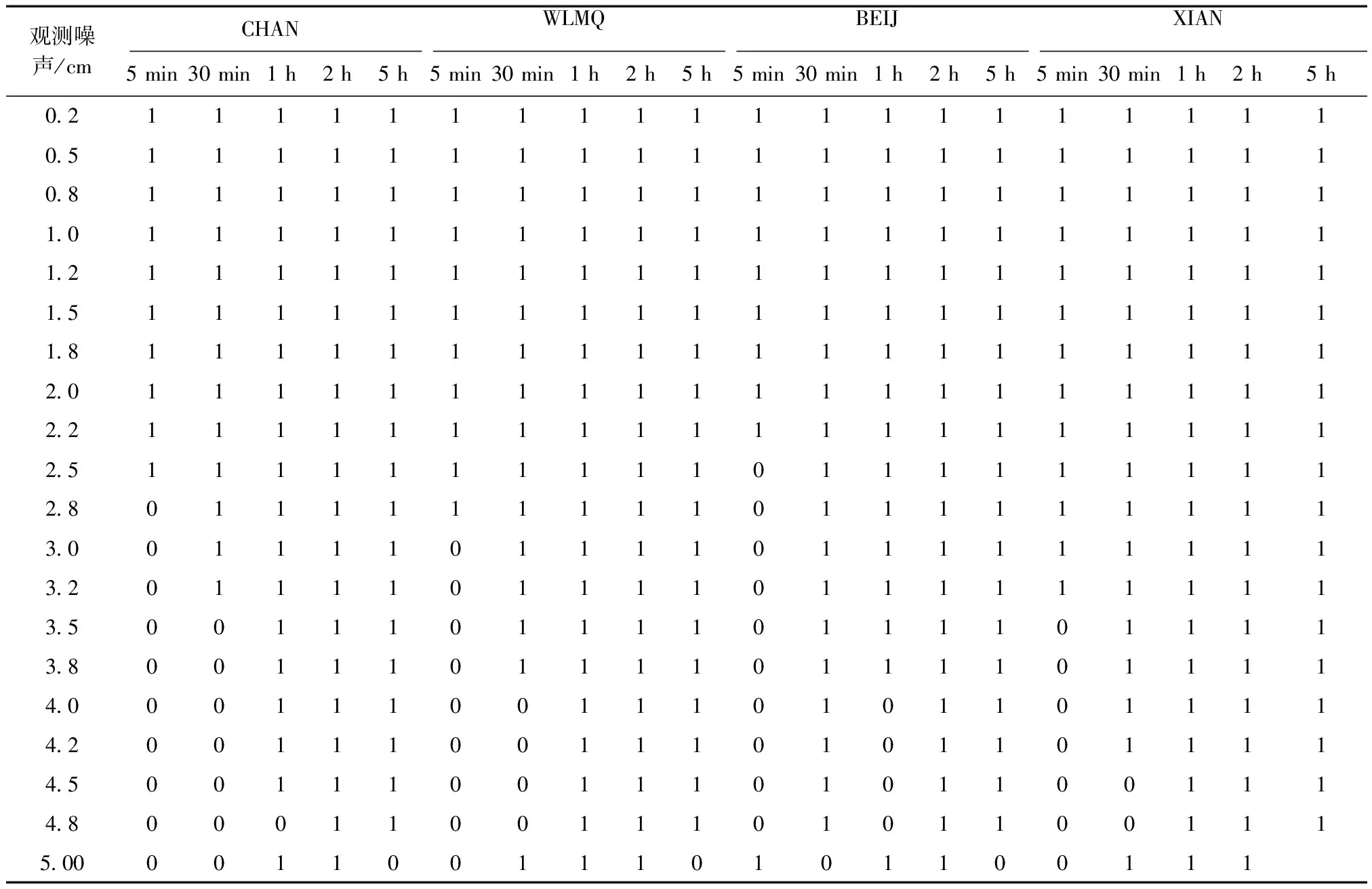
续表3

从表2、表3中可以看出，BDS系统在我国各地区观测时长为2 h以上、观测噪声在5 cm以内时，整周模糊度固定都是正确的，而GPS系统的观测时长为1 h即可；当观测时长较短时，BDS和GPS观测噪声越大，模糊度固定越不正确。

当观测时长为5 min时，在我国各地区模糊度固定正确的BDS系统的观测噪声最大为2 mm ～ 2 cm，而GPS系统的为1～ 3.2 cm，显然当观测噪声较大时，GPS系统比BDS系统更易正确固定模糊度；BDS系统观测时长为30 min、观测噪声最大为1.2～ 3.5 cm时固定的模糊度正确，与GPS观测时长为5 min时相当。

由此可见，观测噪声较大会严重影响BDS系统整周模糊度快速解算的正确性。

2.2 BDS/GPS整周模糊度解算识别的有效性

在实际观测数据处理中，整周模糊度是未知的；在模糊度固定之后，对其正确性需要通过进一步的检验确定：只有通过各项检验，才能确认模糊度的整数解是可靠的，才能回代入原方程重新解算坐标未知数。目前最常用的检验方法是Ratio值检验[20-24]，也称后验方差比检验法，是以固定解中次小和最小残差二次型之比作为检验量，即

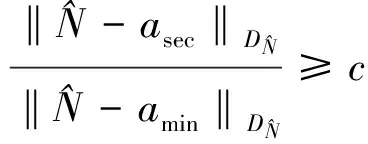
(5)

采用Ratio值检验法对比分析了BDS和GPS观测噪声对我国各地区不同的观测时长载波相位定位整周模糊度固定的影响，结果如图1、图2所示。为便于图形化表示，图中Ratio值大于10的强制设为10。从图中可以看出：在我国各地区相同的观测时长BDS和GPS 2个系统随着观测噪声的增大，Ratio值减小，当Ratio值小于8时，则认为模糊度固定失败；图1中可以看到当观测噪声一定时，BDS系统的Ratio值会随观测时长的增加而增大，但是当观测时长增加到一定程度时Ratio值反而会减小，特别是在我国大部分地区观测时长为5 h时Ratio值比2 h的要小，这主要是由于新星的升起导致模糊度维数增大，造成Ratio值降低；图2中可以看到GPS系统的这种现象会更加明显，GPS卫星运动角速度较快，卫星更替较快，使得大部分地区观测时长大于1 h时的Ratio值明显低于30 min时。

由图1可以看出：BDS系统观测时长为5 min时，在长春地区整周模糊度固定失败，而在其他地区观测噪声最大不超过5 mm时才能够成功固定模糊度；当观测时长为30 min时，在我国大部分地区观测噪声最大不超过1 cm时能够成功固定模糊度，只有在昆明地区观测噪声最大达到1.5 cm时仍然能够成功固定模糊度：由此可见，当观测噪声很大时，BDS系统在我国大部分地区观测时间很短、模糊度不能成功固定，严重影响了模糊度的快速解算。

由图2可以看出，GPS系统观测时长为5 min时，在我国各地区观测噪声最大不超过1 cm时能成功固定模糊度，相当于BDS系统观测时长30 min时能够成功固定模糊度的观测噪声；而GPS观测时长为30 min时，在我国各个地区观测噪声最大不超过1～ 1.5 cm时能成功固定模糊度。

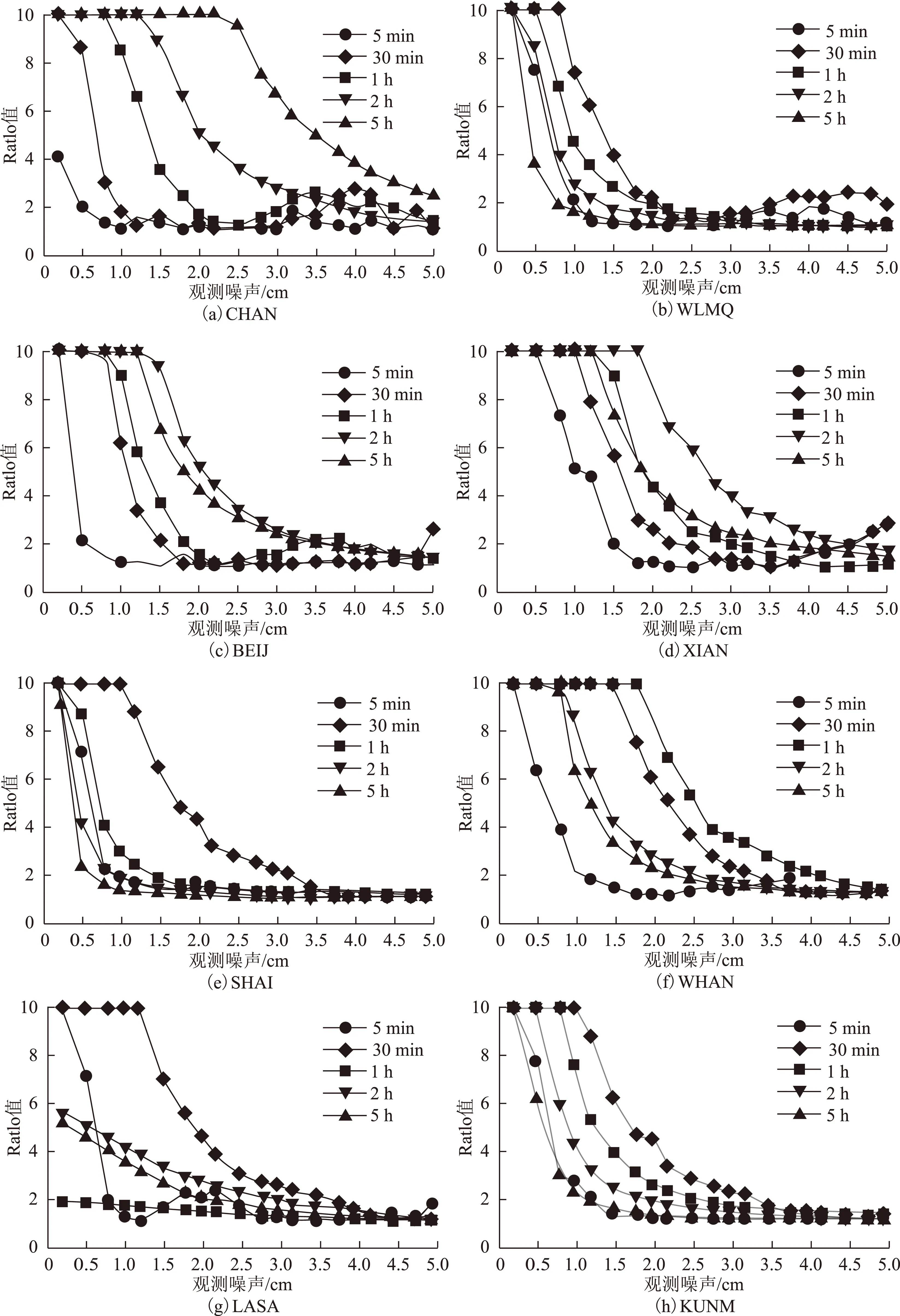
图1 BDS观测噪声对整周模糊度固定Ratio值的影响

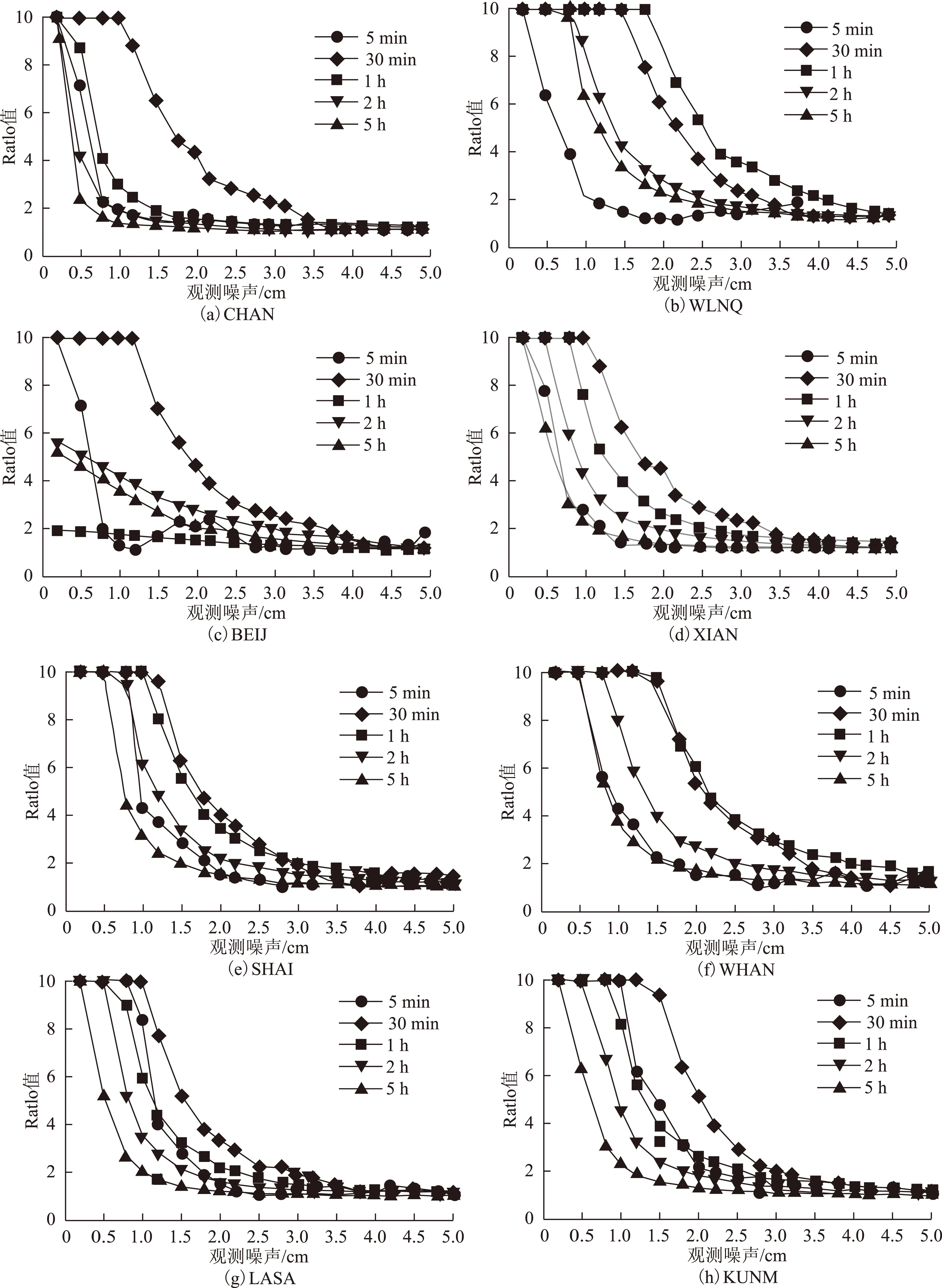
图2 GPS观测噪声对整周模糊度固定Ratio值的影响

3 结束语

本文主要从模糊度是否正确和Ratio值2个方面加以考虑，分析了BDS和GPS不同观测噪声对整周模糊度固定的影响。结果表明：从模糊度固定的正确性来看，BDS载波相位定位观测时间为30 min时，观测噪声最大为1.2～ 3.5 cm时固定的模糊度正确，而GPS观测时长为5 min时观测噪声最大为1～ 3.2 cm；从模糊度识别的有效性来分析，BDS观测时长为30 min时，在我国大部分地区观测噪声最大不超过1 cm时能够成功固定模糊度，而GPS观测时长为5 min时，在我国各地区观测噪声最大不超过1 cm时能成功固定模糊度。因此，无论从模糊度固定的正确性还是模糊度识别的有效性2方面分析，BDS系统在各地区观测时长为30 min时模糊度能成功固定的最大观测噪声与GPS观测时长为5 min时相当，即BDS观测噪声较大、观测时间较短时载波相位定位的模糊度很难成功固定，严重影响BDS系统模糊度的快速解算。

[1] HOFMANN-WELLENHOF B，LICHTENEGGER H，COLLINS J.Global positioning system：theory and practice[M].5th ed.Berlin：Springer-Verlag，2001：319-353.

[2] LEICK A，RAPOPORT L，TATARNIKOV D.GPS satellite surveying[M].3rd ed.New York：John Wiley and Sons，2015：1-10.

[3] TEUNNISSEN P J G，KLEUSBERG A.GPS for geodesy[M].2nd ed.Berlin：Springer Science & Business Media，2012：486-556.

[4] MISRA P，ENGE P.Global positioning system：signals，measurements，and performance[M].2nd ed.Lincoln，MA：Ganga-Jamuna Press，2010：3-28.

[5] HOFMANN-WELLENHOF B，LICHTENEGGER H，WASLE E.GNSS-global navigation satellite systems GPS，GLONASS，Galileo& more [M].Berlin：Springer Science & Business Media.2007：326-351.

[6] 郭秋英，胡振琪.GPS快速定位方程的病态性对整周模糊度及基线解的影响[J].测绘科学，2007，32(2)：42-43．

[7] TEUNNISSEN P J G.Least squares estimation of the integer GPS ambiguity[EB/OL].[2016-01-18].http：//www.citg.tudelft.nl/fileadmin/Faculteit/CiTG/Over-de-faculteit/Afdelingen/Afdeling-Geoscience-and-Remote-Sensing/pubs/PT-BEIJING93.PDF.

[8] TEUNNISSEN P J G.A new method for fast carrier phase ambiguity estimation[EB/OL].[2016-01-18].http：//www.academia.edu/661699/-1994-A-new-method-for-fast-carrier-phase-ambiguity-estimation.

[9] TEUNNISSEN P J G，JONGE D，TIBERIUS C.The lambda method for fast GPS surveying[EB/OL].[2016-01-18].http：//www.docin.com/p-976040446.html.

[10] HAOA W，LIB F.A new method for ill-conditioned diagnosis based on spatial analysis[J].Journal of Information&Computational Science，2010，7(9)：1846-1853.

[11] XU P，SHEN Y，FUKUDA Y，et al.Variance componentestimation in linear inverse ill-posed models[J].Journal of Geodesy，2006，80(2)：69-81.

[12] 邱晓璐，刘根友，段鹏硕，等.BDS/GPS载波相位定位病态性对比分析[J].测绘科学，2015，40(7)：24-28.

[13] 王胜利，王庆，高旺，等.GNSS多系统基线解算中的病态性分析与评价[J].东南大学学报：自然科学版，2013，43(4)：753-757.

[14] GAO Wang，GAO Chengfa，PAN Shugu，et al.Ill-Posedness analysis of ambiguity resolution using BDS-2 and its fusion with GPS[EB/OL].[2016-01-18].http：//link.springer.com/chapter/10.1007/978-3-642-54743-0-32?no-access=true.

[15] 陈永奇.一种检验GPS整周模糊度解算有效性的方法[J].武汉测绘科技大学学报，1997，22(4)：342-345.

[16] 阳仁贵，刘根友，柴艳菊.一种检验GNSS相位模糊度整周解算有效性的方法[J].全球定位系统，2011，36(1)：1-6.

[17] ODIJK D.Fast precise GPS positioning in the presence of ionospheric delays[M].Delft，The Netherlands：Netherlands Geodetic Commission，2002：33-36.

[18] LUO N，LACHAPELLE G.Relative positioning of multiple moving platforms using GPS[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39(3)：936-948.

[19] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件(2.0版)[EB/OL].(2013-12-27)[2016-02-24].http：//www.beidou.gov.cn/attach/2013/12/26/20131226 04a521b35b7f4a54b44cfbbc8abd74a8.pdf.

[20] 邓健，潘树国，赵兴旺.基于可靠性指标的Ratio检验模糊度质量方法[J].测绘科学，2013，38(3)：37-39.

[21] TEUNNISSEN P J G，VERHAGEN S.GNSS carrier phase ambiguity Resolution：challenges and open problem[EB/OL].(2015-12-10)[2016-01-18].http：//link.springer.com/chapter/10.1007/978-3-540-85426-5-90?no-access=true.

[22] TEUNNISSEN P J G，VERHAGEN S.The GNSS ambiguity ratio-testrevisited：a better way of using it[J].Survey Review，2009，41(312)：138-151.

[23] VERHAGEN S，TEUNNISSEN P J G.The ratio test for future GNSS ambiguity resolution[J].GPS Solutions，2013，17(4)：535-548.

[24] TEUNNISSEN P J G.Testing theory-an Introduction[M].Delft：Delft Academic Press，2000：5-20.

Influence analysis of BDS/GPS observation noise on ambiguity resolution

QIU Xiaolu1，LIU Genyou2

(1.Yantai Gold College，Zhaoyuan，Shandong 265400，China；2.Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan，Hubei 430077，China)

Aiming at the problem that observation noise can affect the proper ambiguity resolution，this paper presented using the simulation of observation data to analyze the influence of different observation noises from BDS and GPS respectively on ambiguity resolution from both the correctness of the ambiguity resolution and the effectiveness of ambiguity recognition.The consistency between non-difference and double-difference observation model was utilized，and the ionospheric delay and tropospheric delay errors were ignored.Finally，eight stations which have regional representative in China were selected for experiment.Results indicated that analyzing from both the correctness of ambiguity resolution and effectiveness of ambiguity recognition，the maximum observation noise with ambiguity fixed successfully when the observation time of BDS is 30 min is quite similar with that when GPS is 5 min，showing that the carrier phase positioning ambiguity would be difficult to be fixed successfully when BDS observation noise is larger and the observation time is shorter than that of GPS.

BDS；GPS；carrier phase positioning；observation noise；ambiguity

2016-02-24

国家自然科学基金项目(41321063)；大地测量与地球动力学国家重点实验室基金项目(SKLGED2013-4-1-Z)。

邱晓璐(1989—)，女，硕士，研究方向为GNSS卫星导航定位。

邱晓璐，刘根友.BDS/GPS观测噪声对模糊度解算的影响分析[J].导航定位学报，2016，4(4)：69-76.(QIU Xiaolu，LIU Genyou.Influence analysis of BDS/GPS observation noise on ambiguity resolution[J].Journal of Navigation and Positioning，2016，4(4)：69-76.)

10.16547/j.cnki.10-1096.20160414.

P228

A

2095-4999(2016)04-0069-08