基于非线性干扰观测器的高超声速飞行器离线预测控制方法①
马 宇,蔡远利
(西安交通大学 电子与信息工程学院,西安 710049)
基于非线性干扰观测器的高超声速飞行器离线预测控制方法①
马 宇,蔡远利
(西安交通大学 电子与信息工程学院,西安 710049)
针对高超声速飞行器存在参数不确定和外界强干扰的纵向非线性模型,结合非线性干扰观测器的干扰辨识能力和离线预测控制显式处理系统约束的优点,提出一种基于非线性干扰观测器的离线预测控制方法。首先针对标称情况下的纵向模型,引用多面体不变集理论,设计离线预测控制器;然后在存在干扰的情况下,采用非线性干扰观测器估计未知干扰,并设计合适的补偿增益,对离线预测控制器进行补偿,提高其鲁棒性。仿真结果表明,该控制器不仅能够有效抑制干扰,而且保证系统状态和控制输入在给定的约束范围内,实现速度和高度指令的精确跟踪。
高超声速飞行器;离线预测控制;多面体不变集;非线性干扰观测器
0 引言
高超声速飞行器因其临近空间高超声速飞行(Ma>5)的特性,成为国内外航空航天领域的研究热点。目前,以超燃冲压发动机为基础的吸气式高超声速飞行器取得突破性进展。由于其动力系统与机体一体化设计的独特气动外形,使得空气动力系统和发动机之间强非线性耦合,给高超声速飞行器的控制系统设计带来巨大挑战[1]。
近年来,针对高超声速飞行器自身强非线性和强耦合特性,以及参数不确定和外界环境的干扰影响,以其纵向动力学模型[2]作为研究对象的控制系统已经取得很大进展。许多先进的控制方法已应用到控制系统设计中,包括鲁棒控制[2-4]、自适应控制[5-6]、自适应滑模控制[7]、反演控制[8-9]、LPV鲁棒变增益[10]、拟连续积分高阶滑模[11]等控制器设计。对于复杂的飞行环境引起的较大参数不确定,许多学者以人工智能方法为基础,估计高超声速飞行器的强非线性动态和参数不确定性,提出基于神经网的控制器[12]和基于模糊系统的控制器[13]。尽管这些控制器在不同方面改进跟踪性能和对不确定参数的鲁棒性,但在面对额外强干扰时,仅以牺牲标称的控制性能为代价,通过一种相对缓慢的方式被动的反馈调节来抑制干扰。在控制器设计时,为了直接考虑干扰抑制,文献[14]引入非线性干扰观测器估计未知干扰,并设计合适的补偿增益,获得新的补偿控制量,从而达到直接干扰抑制的目的。
考虑攻角等约束的满足程度是影响超燃冲压发动机工作性能的主要因素,因此控制系统设计时,系统约束的满足至关重要。然而,上述控制方法只能通过仿真参数调节来验证系统约束的满足程度,都没有在控制器设计时直接考虑系统约束。MPC作为工业领域处理系统约束的有效方法,在控制系统设计阶段就可以考虑可能的约束限制,在保证系统约束的同时,可获得良好的控制性能。为了克服其在线优化计算量大的问题,文献[15]基于鲁棒约束模型预测控制[16],利用椭圆不变集渐近稳定的性质,将在线优化转为离线,在线插值获得相应的控制量,极大地减少了计算量。文献[17]采用多面体不变集设计离线预测控制方法,避免了椭圆不变集处理不等式约束的保守性,不仅可以处理不对称约束,且扩大了初始可行域。该方法是基于标称系统的,单纯依靠控制方法本身的鲁棒性来保证干扰系统的稳定是很困难的,尤其是在受到强干扰情况下,系统往往不能够保持稳定。
本文基于多面体不变集的离线预测控制,引入非线性干扰观测器[14],设计复合控制器,增强干扰抑制能力。首先,通过小扰动线性化获得标称模型,并设计离线预测控制器。然后,针对存在强干扰的非线性系统的仿射模型,设计干扰观测器估计未知干扰,并设计合适的补偿增益,获得补偿控制量,构成新的复合控制器。最后,理论证明新的复合控制器使系统闭环稳定,并仿真验证其有效性。
1 模型及问题描述
1.1 高超声速飞行器运动模型
本文以文献[2]的高超声速飞行器纵向动力学模型作为研究对象,该模型是由 NASA兰利研究中心(LaRC)研发并对外公布的,采用关于飞行速度V、航迹角γ、高度h、攻角α和俯仰角速率q的五阶非线性微分方程来描述纵向动力学模型,即
(1)
其中,di(i=1,…,5)为额外未知的干扰(理论上,d3=0,d4=0);T、L、D、Myy、r分别为推力、升力、阻力、气动力力矩和飞行器离地心的距离,其相关定义如下:
(2)
式中CL、CD、CT分别为升力、阻力及推力系数;CM(α)、CM(δe)和CM(q)分别为与攻角、升降舵偏转角、俯仰角速率相关的力矩系数。
本文针对高超声速飞行器在巡航段设计控制器,空气动力系数在巡航段平衡点(M=15,V=4 590.3 m/s,h=33 528 m,γ=0(°)/s,q=0(°)/s)可简化为
(3)
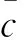
1.2 问题描述
本文主要针对标称模型(无干扰)设计离线预测控制器,通过非线性干扰观测器对系统的未知干扰估计,添加干扰补偿项,达到对未知干扰的抑制效果。为了使控制器设计过程简洁,本文将高超声速飞行器的非线性纵向动力学模型(1)重新描述为一个MIMO的非线性系统,即
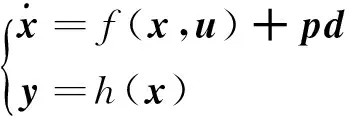
(4)
其中,x=[V,γ,h,α,q]T∈Rn为状态向量,n=5;u=[β,δe]T∈Rm为控制输入向量,m=2;d=[d1,d2,d3,d4,d5]T为干扰向量;p为I5×5;h(x)=[V,h]T;f(x,u)为关于x和u的光滑函数,且连续可微。
(5)
首先设计离线预测控制器,不考虑系统未知干扰,非线性模型为
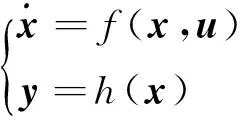
(6)

以一阶Taylor展开为理论基础,可获得平衡点附近邻域内的小扰动线性模型,即
(8)
其中,[At,Bt]为Jacobian矩阵[∂f/∂x,∂f/∂u]在平衡点处的值。
(9)
(10)
由于离线预测控制器是基于离散模型设计的,因此对线性连续模型(8)进一步离散化可得线性离散模型如下:
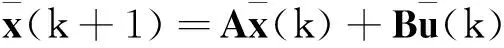
(11)
其次,为了便于干扰观测器设计,采用一阶Taylor线性化的方法获得原非线性系统(4)的仿射模型,即
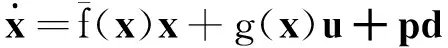
y=Cx
(12)

(13)
(14)
其中,
2 控制器设计与分析
2.1 基于多面体不变集的离线预测控制
对于标称线性离散模型(11),设计状态反馈控制律:
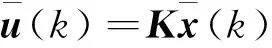
(15)
同时满足如下min-max性能指标:
(16)
其中,Θ和R为对称的权系数矩阵。状态约束和控制约束为
(17)
文献[15]利用椭圆不变集渐近稳定的性质,选择一系列离散的状态点,将式(16)中带有状态和控制约束的min-max优化问题转化为一组含有LMI的凸优化问题,离线获得包含离散状态点的最大椭圆不变集及其对应的状态反馈控制增益,在线凸组合当前状态相邻的两个椭圆不变集对应的控制增益获得控制律。本文借鉴文献[15]的设计思想,采用基于多面体不变集的离线预测控制方法[17]设计控制器。该方法避免了椭圆不变集处理不等式约束的保守性,不仅可处理不对称约束,而且扩大了初始可行域。为了便于该方法的研究,首先给出多面体不变集的定义。
定义1[17]对于给定集合S={x|Mx≤d},设k时刻状态x(k)∈S,如果以后任何时刻的状态都属于集合S,即x(k+i)∈S,∀i=1,2,…,∞,则称S为多面体不变集。
根据定义1,该方法离线构造一系列状态反馈控制增益对应的多面体不变集序列,在线时选择当前状态所在最小多面体不变集对应的控制增益计算控制量。
算法1
【离线计算】

(2)选择(Mi,di)的第m行(Mi,mdi,m),求解如下最优问题:
(18)
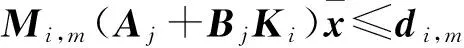
(3)令m=m+1,返回(2),直到m大于约束(Mi,di)的行数。保存反馈控制增益及对应的多面体不变集{Ki,Si}。
【在线计算】



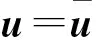
(19)
2.2 非线性干扰观测器设计
本文采用文献[18]提出的非线性干扰观测器:
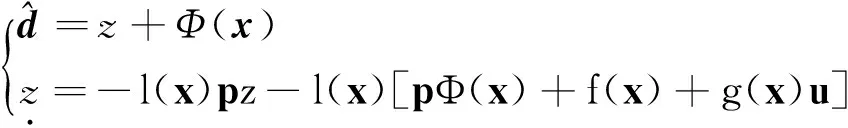
(20)
其中,z和Φ(x)分别为非线性干扰观测器的内部状态和非线性向量值函数;l(x)为非线性观测器增益,定义为
(21)

(22)
引理2[19]在假设1满足的情况下,如果选取的非线性观测器增益l(x)使
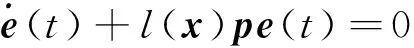
(23)
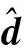
2.3 稳定性分析
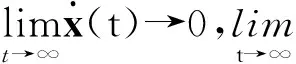
假设2 原点为标称非线性系统的平衡点,即xeq=0,ueq=0。本文提出的离线预测控制器(15)能保证系统在原点附近闭环稳定,系统状态渐近稳定于原点。
(1)满足假设1和假设2的条件;
(2)非线性观测器增益l(x)使系统(23)渐近稳定;
(3)设计补偿增益
使g(x)β(x)+p在工作点附近连续可微。
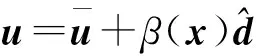

(24)
其中
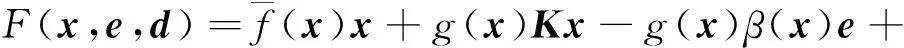
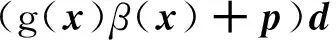
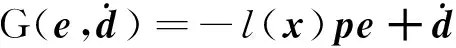


(25)
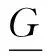
接下来,进一步证明控制器的干扰补偿项能够抑制干扰的影响,即复合控制器使干扰系统的状态趋于原点。

(26)
令C=In×n,将条件(3)中的补偿增益β(x)带入式(26)可得
(27)
3 仿真实验与分析
针对高超声速飞行器的非线性系统在参数不确定和外界未知干扰的情况下,采用本文所提出的复合控制器使速度和高度跟踪指令信号。速度的初始值为4 590.288m/s,高度的初始值为33 528m,跟踪指令信号分为2种情况。
Case1:定速、定高跟踪飞行,速度和高度的跟踪指令信号分别为4 680.288m/s,33 618m;
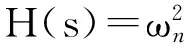
对于标称模型,离线预测控制方法采用的对称权系数矩阵分别为Θ=diag{1 0.1 1 0.1 0.1},R=diag{50 50}。因为本文主要考虑速度和高度指令信号的跟踪,所以算法1在离线构造一系列状态反馈控制增益对应的多面体不变集序列时,仅选择速度和高度2个状态量的离散状态点,即
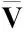
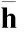
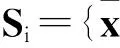
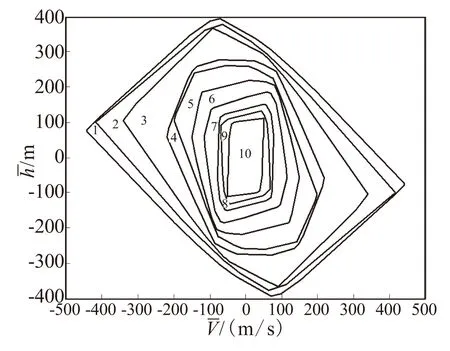
图1 算法1离线计算的多面体不变集序列在速度 和高度二维坐标平面的投影Fig.1 Projection of polyhedral invariant sets-constructedoff-line by algorithm 1 in velocity and height of2D coordinate plane
对于干扰模型,本文选取的非线性观测器增益为l(x)=10I5×5。未知外界干扰设定:当t≥20s时,d1=-10,d3=0;当t≥40s时,d2=0,d5=0.2+0.1sin(0.1πt+π)以及d4=0.05。参数不确定设定如文献[7],即
Case1:本文以Intel 奔腾双核E2200上的Matlab 2012(b)作为仿真平台,仿真步长为0.01 s,控制步长为0.01 s,采用3种方法进行对比分析。在所进行的80 s仿真时间中,自适应滑模控制方法的仿真运行时间为6.072 3 s,本文方法的仿真运行时间为4.316 1 s,离线预测控制方法的仿真运行时间为1.743 8 s。仿真结果如图 2~图 4所示,在前20 s无外加干扰的情况下,本文方法与离线预测控制方法的响应曲线基本重合,因此本文方法可获得与离线预测控制方法一致的标称控制性能。从图 2可明显看出,相比于自适应滑模控制方法,本文方法和离线预测控制方法能使高超声速飞行器更快地跟踪速度和高度的参考指令,速度和高度的超调量相对较高,但在可接受范围内,因此具有更好的跟踪性能。从图 3和图 4可看出,3种方法均能使攻角、节流阀设定值和升降舵偏转角满足给定约束,然而自适应滑模控制方法需要根据经验设定控制参数,在实际的工程应用中,为了保证状态和控制变量满足给定约束,往往需要额外地增加限幅器实现。本文方法和离线预测控制方法在设计时就考虑了状态和控制变量约束,因此无需根据人工经验设定,满足系统对约束处理的要求。对于3种方法的干扰抑制能力,从图 2可明显看出,在20 s后,系统受干扰影响,离线预测控制方法和自适应滑模控制方法不再精确跟踪参考指令,不仅存在稳态误差,而且在一定程度上已经发散。然而,本文方法具有出色的干扰抑制能力,使系统在干扰影响下,仍获得良好的速度和高度跟踪性能。

图2 速度和高度跟踪曲线Fig.2 Tracking curves of velocity and altitude
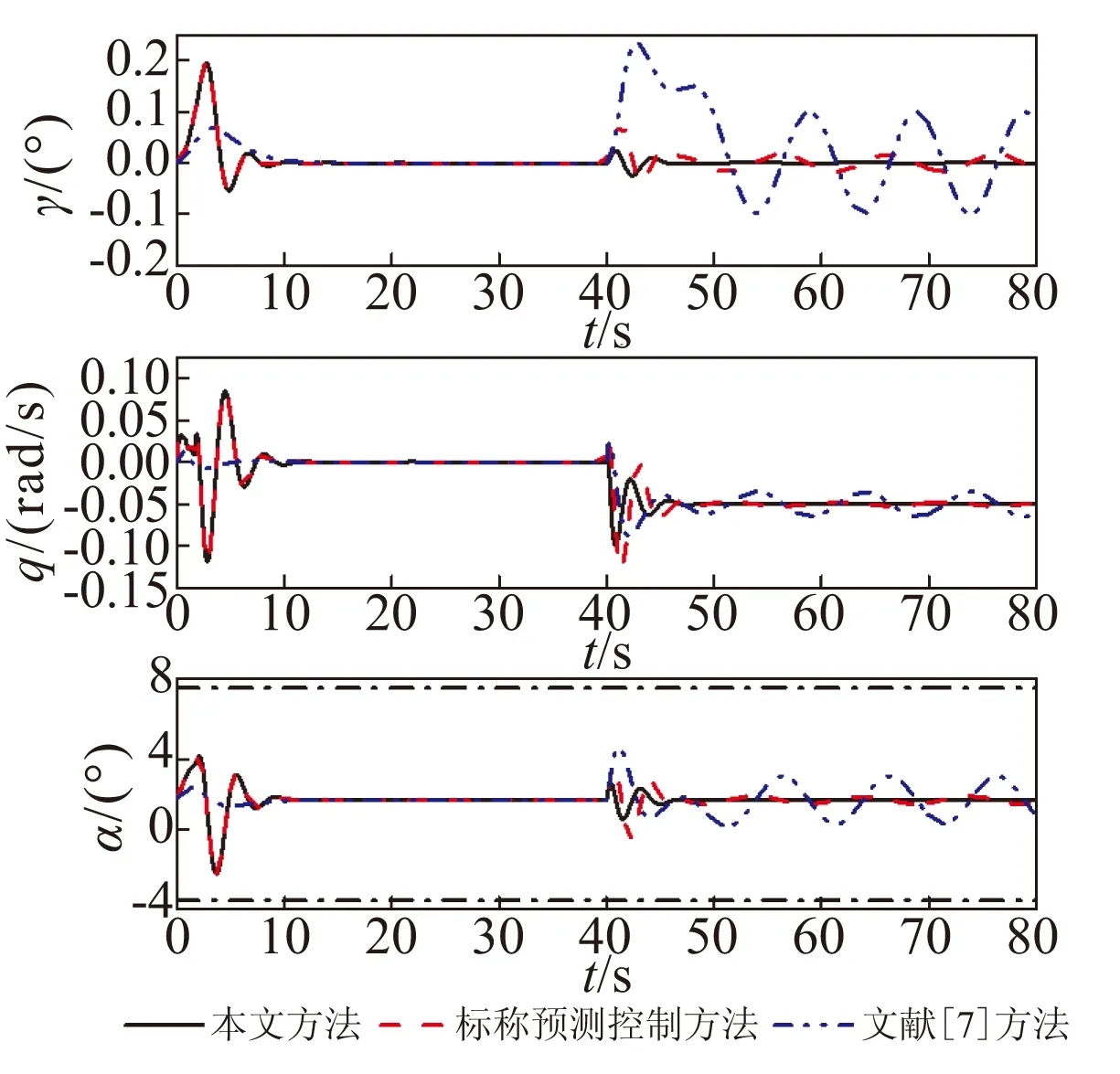
图3 航迹角、俯仰角速率及攻角响应曲线Fig.3 Response curves of flight-path angle, pitch rate and angle of attack

图4 控制输入Fig.4 Control inputs
Case2:与Case1的仿真条件一致,采用3种方法使高超声速飞行器跟踪速度和高度的动态指令信号,仿真结果如图 5和图 6。从图 5可明显看出,相比于自适应滑模控制方法,本文方法和离线预测控制方法具有更快地跟踪性能,而且本文方法比其他两种方法的抗干扰抑制能力强。如图 6所示,3种方法均能使攻角、节流阀设定值和升降舵偏转角满足给定约束。
上述仿真结果表明,本文方法在保证系统约束的情况下,具有出色的干扰抑制能力和良好的跟踪性能,且仿真运行时间少于自适应滑模控制方法,满足高超声速飞行器对控制系统的实时性要求。
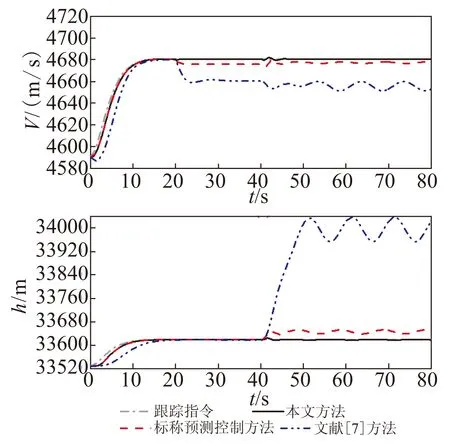
图5 速度和高度跟踪曲线Fig.5 Tracking curves of velocity and altitude
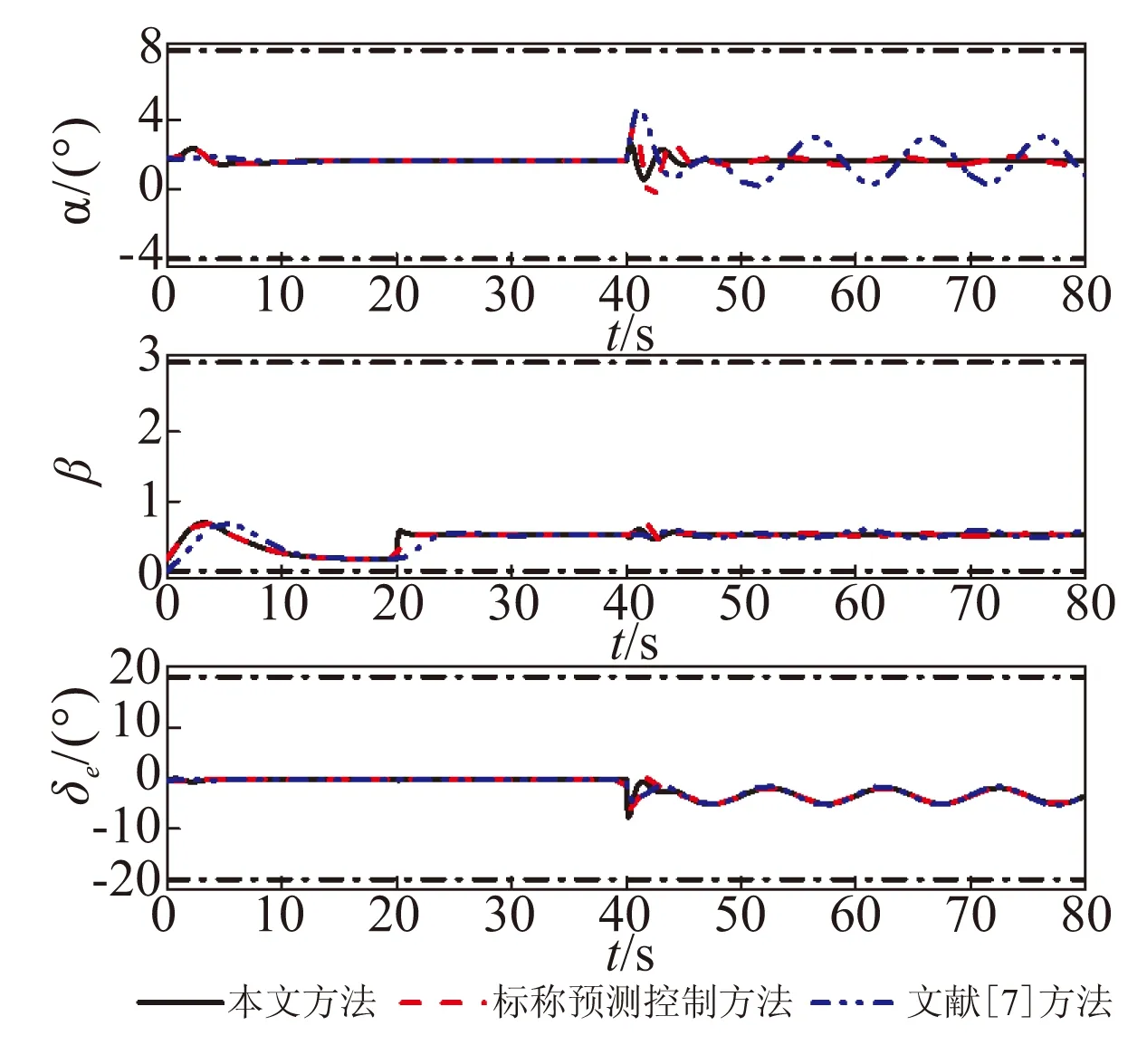
图6 攻角响应曲线及控制输入Fig.6 Response curves of angle of attack and control inputs
4 结论
(1)针对高超声速飞行器对系统状态和控制输入约束的要求,本文引用多面体不变集理论,提出了离线预测控制方法,显式地处理约束问题,无需根据人工经验进行复杂的参数设定。该方法通过离线计算一系列多面体不变集及其对应的状态反馈增益,减少在线计算量,满足高超声速飞行器对控制系统的实时性要求。
(2)对于单一的离线预测控制器鲁棒性较弱的问题,采用干扰观测器估计未知干扰,并设计合适的补偿增益,获得离线预测控制器的补偿控制量,增强干扰抑制能力。
(3)通过对高超声速飞行器跟踪速度和高度指令的仿真结果分析,验证了该复合控制器的优越性。
[1] 闫杰,于云峰,凡永华,等.吸气式高超声速飞行器控制技术 [M].西安: 西北工业大学出版社,2014.
[2] Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,2000,23(4): 577-585.
[3] Marrison C I,Stengel R F.Design of robust control systems for a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,1998,21(1): 58-63.
[4] Sigthorsson D,Jankovsky P,Serrani A,et al.Robust linear output feedback control of an airbreathing hypersonic vehicle [J].Journal of Guidance,Control,and Dynamics,2008,31(4): 1052-1066.
[5] Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J].Journal of Guidance,Control,and Dynamics,2009,32(2): 402-417.
[6] Fiorentini L,Serrani A.Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model [J].Automatica,2012,48(7): 1248-1261.
[7] Xu H,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle [J].Journal of Guidance,Control,and Dynamics,2004,27(5): 829-838.
[8] 时建明,王洁,王琨,等.吸气式高超声速飞行器纵向运动反演控制器设计 [J] .西安交通大学学报,2013,47(3): 102-107.
[9] 卜祥伟,吴晓燕,白瑞阳,等.基于滑模微分器的吸气式高超声速飞行器鲁棒反演控制 [J].固体火箭技术,2015,38(1): 12-17.
[10] 秦伟伟,郑志强,刘刚,等.高超声速飞行器的 LPV 鲁棒变增益控制 [J].系统工程与电子技术,2011,33(6): 1327-1331.
[11] Wang J,Zong Q,Tian B,et al.Flight control for hypersonic vehicle based on quasi-continuous integral high-order sliding mode [C]// 24th Chinese Control and Decision Conference (CCDC),Taiyuan,China.IEEE,2012: 2185-2190.
[12] Xu B,Gao D X,Wang S X.Adaptive neural control based on HGO for hypersonic flight vehicles [J].Science China Information Sciences,2011,54(3): 511-520.
[13] Gao D X,Sun Z Q.Fuzzy tracking control design for hypersonic vehicles via TS model [J].Science China Information Sciences,2011,54(3): 521-528.
[14] Yang J,Zhao Z,Li S,et al.Composite predictive flight control for airbreathing hypersonic vehicles [J].International Journal of Control,2014,87(9): 1970-1984.
[15] Wan Z,Kothare M V.An efficient off-line formulation of robust model predictive control using linear matrix inequalities[J].Automatica,2003,39(5): 837-846.
[16] Kothare M V,Balakrishnan V,Morari M.Robust constrained model predictive control using linear matrix inequalities [J].Automatica,1996,32(10): 1361-1379.
[17] Bumroongsri P,Kheawhom S.An off-line robust MPC algorithm for uncertain polytopic discrete-time systems using polyhedral invariant sets [J].Journal of Process Control,2012,22(6): 975-983.
[18] Chen W H,Ballance D J,Gawthrop P J,et al.A nonlinear disturbance observer for robotic manipulators[J].IEEE Transactions on Industrial Electronics,2000,47(4): 932-938.
[19] Chen W H,Guo L.Analysis of disturbance observer based control for nonlinear systems under disturbances with bounded variation [C]//Proceedings of International Conference on Control,Bath,England,2004.
[20] Khalil H K,Grizzle J W.Nonlinear systems [M].New Jersey: Prentice hall,1996.
(编辑:吕耀辉)
Nonlinear-disturbance-observer-based offline model predictive control for hypersonic vehicles
MA Yu, CAI Yuan-li
(School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710064, China)
Combining the identification capability of nonlinear disturbance observer and the advantages of offline model predictive control for handling the constraints, a nonlinear-disturbance-observer-based offline model predictive control strategy was developed for a hypersonic vehicle subject to the parameters uncertainties and external strong disturbances. Firstly, according to the theory of polyhedral invariant set, an offline model predictive controller was designed for the nominal longitudinal model. Then a nonlinear disturbance observer was introduced to estimate the unknown disturbances for the longitudinal model in the presence of strong disturbances, and the compensation gain matrix was properly designed to enhance the robustness of the offline model predictive controller. Simulation results demonstrate that the proposed controller not only obtains promising robustness and disturbance rejection performance but also realizes accurate tracking of velocity and altitude commands without the violation of the state and control constraints.
hypersonic vehicle;offline model predictive control;polyhedral invariant set;nonlinear disturbance observer
2015-09-09;
2015-11-18。
宇航动力学国家重点实验室开放基金(2011ADL-JD0202);国家自然科学基金项目(61202128;61463029)。
马宇(1988—),男,博士生,研究方向为飞行器制导与控制。E-mail:myuyu1@stu.xjtu.edu.cn
蔡远利(1963—),男,教授,博士生导师,从事现代控制理论及应用、复杂系统建模与仿真的研究。E-mail:ylicai@mail.xjtu.edu.cn
V448
A
1006-2793(2016)06-0825-08
10.7673/j.issn.1006-2793.2016.06.016

