高凝相浓度喷管两相流研究进展①
刘平安,王 良,王 璐,王 革,郜 冶
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
高凝相浓度喷管两相流研究进展①
刘平安,王 良,王 璐,王 革,郜 冶
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
为了选择合适的方法研究高金属含量发动机喷管内的高凝相浓度两相流,从理论研究和实验研究两个方面,总结了喷管两相流研究的进展,根据各种方法的研究结果,讨论了各方法对高凝相浓度喷管两相流研究的参考价值。发现实际流动介于两相平衡流和两相冻结流之间,在高凝相浓度喷管两相流中,颗粒含量高,两相间相互作用强,流动趋于等温,两相等温流模型适用于简化分析。两相流数值模型包括颗粒轨道模型和颗粒拟流体模型,两者均可用于高凝相浓度喷管两相流计算,轨道模型忽略颗粒体积,但能描述颗粒的运动变化过程,拟流体模型能得到颗粒参数在空间的分布。两相流实验研究主要用于验证数值计算的结果,并从实验获得颗粒粒径、颗粒阻力系数、Nu数等参数,以用于理论计算。采用理论和实验相结合的方法,分析颗粒或两相流场的某些局部特征,最终可推广到整个喷管内,从而大大减少实验难度。通过分析喷管两相流的研究进展,为高金属含量发动机内高凝相浓度喷管两相流的研究提供了参考。
喷管两相流;高凝相浓度;固体火箭发动机
0 引言
铝、镁等金属很早就作为燃烧剂用于固体推进剂中,提高了发动机性能[1-2]。发动机性能提升程度受金属使用量和粒径的影响,随着推进剂的发展,金属含量逐渐增加,粒径从微米级向纳米级过渡。在纳米铝冰发动机和金属燃料冲压发动机的推进剂中,金属含量达到40%~50%,其燃烧产物中凝相氧化物含量也高达94%,这类发动机被称为高金属含量发动机[3-5]。金属燃料的使用,使发动机工作效率下降,且其含量越高,效率下降越多[6-7]。发动机工作效率是由热力计算的理论性能与实测性能比较得到的,工作效率越高的发动机,理论性能预估越准确。如果用比冲效率来衡量,当发动机中金属含量低于30%时,其比冲效率大于90%,性能预估较准确[8],而金属含量为50%的铝冰发动机,实测比冲效率仅为56%~60%,性能预估不准[9]。
铝冰发动机工作效率低,性能预估不准,导致预先研究时实验屡屡失败。因此,必须研究这类发动机性能损失的成因。在所有含金属发动机中,由金属燃料带来的损失包括燃烧不完全损失和两相流损失。一般而言,金属的燃烧效率很高,燃烧不完全损失很小,如在复合推进剂发动机中,金属燃烧效率在96%以上[10];在铝冰发动机中,金属燃烧效率也大于85%[11]。另一方面,两相流损失是喷管膨胀过程的主要损失,对发动机性能影响很大,且两相流凝相浓度越大,两相流损失越大[8]。由此可见,两相流研究是含金属发动机性能损失研究的重点。在高金属含量发动机中,推进剂燃烧产物中颗粒很多,两相流凝相浓度很大。如铝冰推进剂发动机的喷管中颗粒含量可达94%[12],在金属镁水冲压发动机中,水燃比为0.5时,在喷管中颗粒含量达50%[13]。一般认为,凝相颗粒含量大于50%的喷管流动为高凝相浓度两相流,这在高金属含量发动机的喷管中很常见。高凝相浓度两相流带来较大的两相流损失,这是高金属含量发动机性能损失的主要原因。
为了合理评估高凝相浓度喷管两相流损失及其对发动机性能的影响,并最终找到准确预估发动机工作性能的方法,本文从理论和实验两方面,总结了发动机喷管两相流研究的进展。鉴于专门针对高凝相浓度喷管两相流的研究很少,在总结各个研究方法之后,还讨论了各种方法对高凝相浓度喷管两相流研究的参考价值。
1 喷管两相流理论研究的进展
为了计算发动机的理论性能,必先得到喷管两相流场参数,而求解控制方程得到流场参数的过程,即为喷管两相流理论研究。喷管两相流控制方程描述了颗粒速度up、颗粒温度Tp、气相速度ug、气相温度Tg间关系及其随时间空间的变化。
在适当的假设下,一维矢量形式的控制方程组如下[14]:
(1)
其中,U、F和S分别为待求未知量矩阵、通量矩阵和源相矩阵,形式如下:
式中ms为相间质量源相;p为压强;τv为颗粒的动量松弛时间;τv=mp/[3πμrp·f(Rep)];τT为颗粒的热松弛时间,表示为τT=mpCp/[2πrpλ]。
喷管两相流求解的入口条件为Tg=Tp=T0,ug=up=u0,p=pc,出口条件为p=pe。其中,T0为发动机燃烧室温度,u0为喷管头部的平均流速,pc为燃烧室压强,通常认为燃烧室到喷管头部压强变化很小,喷管头部压强用燃烧室压强表示,pe为喷管出口压强。确定求解条件之后,可用解析模型或数值模型,求解两相流控制方程,得到喷管两相流场参数,用于发动机性能计算。1.1 喷管两相流解析模型的研究
在早期研究中,研究人员试图通过简化假设,得到两相流控制方程的解析解。从颗粒与燃气间速度、温度的关系来看,颗粒相对燃气可能处于4个状态,分别是平衡、冻结、滞后和非平衡。“平衡”表示两相速度相等、温度相同,即ug=up,Tg=Tp;“冻结”表示燃气或颗粒的速度或温度保持入口时的值(u0、T0)不变,其中颗粒速度冻结表示计算不考虑颗粒的影响;“滞后”是颗粒温度比燃气高,速度比燃气低的现象,此处特指颗粒参数与燃气参数呈一定已知函数关系的情况;“不平衡”表示颗粒虽然滞后于燃气,但颗粒参数与燃气参数的关系不能确定,颗粒参数与燃气参数是两组独立的变量。当两相间速度或温度关系为平衡、冻结或滞后时,原本要求解的两组参数(ug和up,Tg和Tp)变成了一组参数(u,T),求解过程将被大大简化。采用这种方法,可得到两相流控制方程的解析解。
为了便于分析,定义颗粒的速度滞后数为(1-K),其中K为两相速度系数,K=up/ug;颗粒的温度滞后数为(1-L),其中L为两相温度系数,L=(T0-Tp)/(T0-Tg)。用K和L替换变量up和Tp,在适当的假设下,把颗粒参数变换为气相参数的等效形式,由此可通过理论推导得到喷管两相流的解析解。已有研究成果可按不同K和L值列为表1中的各个解析模型。表1中,Dk为扩散系数;C1、C2表示K或L为常数;“×”表示系数未定;Tg或Tp等于T0表明,燃气或颗粒温度保持不变。
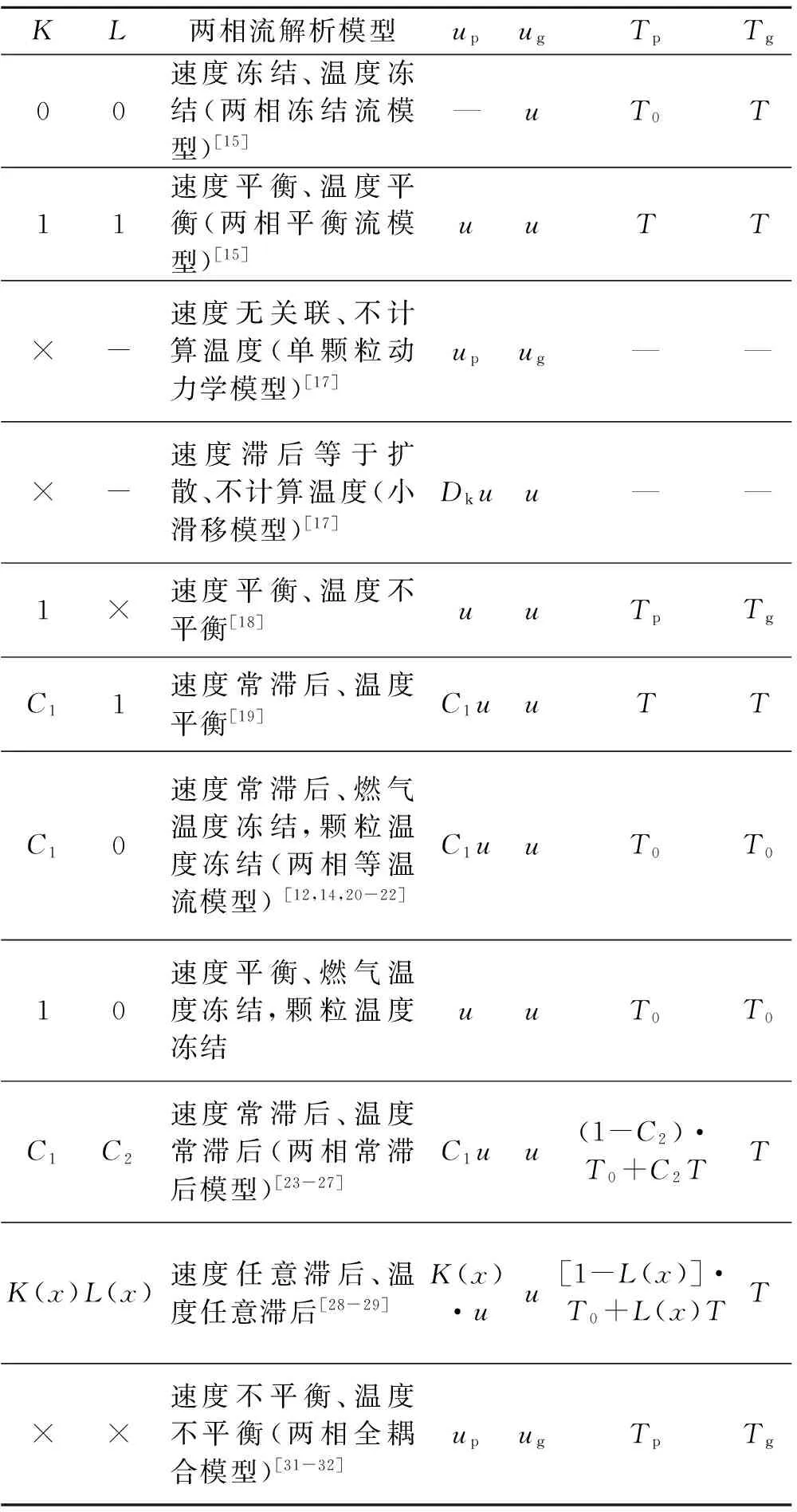
表1 喷管两相流的解析模型Table 1 Analytic models for two-phase nozzle flow
上述解析模型主要可分为4类:无滞后/冻结模型、单种滞后模型、等温流模型、全滞后模型。下面将分别进行阐述。
(1)无滞后/冻结模型
不考虑/过分考虑颗粒参数与燃气参数不相等的情况,主要包括两相冻结流模型和两相平衡流模型[15]。从表1中可看出,在这些模型下,颗粒和气相的参数变成了已知参数或一组未知参数(u、T),因此很容易求解析解。但在实际情况下,颗粒由于具有高密度和热惰性,在随燃气通过喷管的过程中,其速度和温度不可能与燃气相同。因此,这类模型存在固有的局限性。“两相平衡流模型”常用于喷管热力计算[16],可得到发动机的最大理论性能,如发动机比冲。“两相冻结流模型”假设燃气流动不受颗粒影响,由于忽略了其贡献的推力,计算得到的发动机理论性能很低。这两种模型是喷管两相流的极限情况,计算得到的发动机理论性能参数值分别为最大和最小,实际流动位于两者之间。在高凝相浓度喷管两相流中,颗粒对燃气流动影响很大,且颗粒向外排出产生推力,是发动机推力的重要来源。因此,两相冻结流模型并不适用。而当颗粒增多时,两相间耦合作用增强,两相接近平衡态,平衡流模型可用于分析高凝相浓度喷管的最大理论性能。
(2)单种滞后模型
单种滞后模型只计算速度和温度滞后中的一种,要么假定另一项平衡。相比无滞后/冻结模型,考虑了颗粒的滞后效应,主要包括单颗粒动力学模型、小滑移模型[17]、速度平衡温度不平衡模型[18]、速度常滞后温度平衡模型[19]。
在冻结流模型的基础上,“单颗粒动力学模型”用已经求得的气相流场计算颗粒沿轨道的参数。“小滑移模型”假设两相间速度滞后等于颗粒作为混合物组元的扩散。这两个模型均不考虑颗粒和燃气的温度,在喷管两相流中使用很少。为此,研究人员假定两相速度或温度平衡,仅讨论一种滞后对结果的影响。Soo[15]发现,速度滞后对发动机性能影响更大,而线性加速假设能简化非平衡情况的求解。Dillon[18]则在速度平衡假设下,对两相凝相浓度为8的喷管进行计算,提出了“速度平衡温度不平衡”模型,说明在高凝相浓度下,颗粒与燃气温度不平衡较小。于是,研究重点转向了速度不平衡。Gilbert等[19]提出了“速度常滞后温度平衡”模型,该模型采用了气相线性加速的假设。计算结果发现,颗粒粒径越大,速度滞后越大,发动机性能下降越多。这说明速度滞后对燃气在喷管中的膨胀过程影响很大。由于仅考虑了一种滞后,单种滞后模型目前已很少用,对高凝相浓度喷管两相流计算的参考价值不大。
(3)等温流模型
等温流模型是单种滞后模型的特殊情况。当喷管两相流中凝相的浓度很大时,由于颗粒多,两相间热交换量大,燃气和颗粒的温度可能保持平衡,且在流动过程中保持不变,即燃气和颗粒的温度均被“冻结”,这种现象称为喷管的“等温膨胀”。在温度冻结假设下,研究模型包括速度常滞后且燃气颗粒温度均冻结模型(速度常滞后等温流模型)、速度平衡且燃气颗粒温度均冻结模型(速度平衡等温流模型)。
其中,“速度常滞后等温流模型”最常用于喷管中,由Rudinger[20-21]提出,迟伟等[12,14,22]用其解决了实际喷管流动问题。该模型求解方法简单,凝相浓度较大(η=0.1~17)时,能得到准确的计算结果,适用于喷管两相流的简化计算。当凝相浓度更大时,需要考虑颗粒体积的影响。另外,研究发现凝相浓度越大,两相速度越接近平衡,因此提出“速度平衡等温流模型”。在高凝相浓度喷管两相流计算中,应以等温流为前提,颗粒速度滞后与速度平衡的等温流模型均可采用。对于铝冰发动机的喷管,由于两相流凝相浓度高达17,应采用速度平衡的等温流模型。
(4)全滞后模型
全滞后模型完整地考虑了颗粒速度和温度滞后,包括两相常滞后模型、两相任意滞后模型和两相全耦合模型。“两相常滞后模型”假定两相间温度和速度滞后数为常数,即K=C1,L=C2[23-27];“两相任意滞后模型”假定滞后数为喷管轴向坐标x的特定函数,即K=K(x),L=L(x),采用逆解法求解[28-29]。这2个模型均把两相控制方程简化为等效单一流体方程求解,但都需指定K和L,模型被过分简化,计算结果与实际有较大偏差。因此,在实际计算中应用很少[30]。“两相全耦合”模型不需指定K或L,而采用变量替换和迭代法直接求解控制方程,得到燃气和颗粒各自参数[31-33]。因此,其与实际更接近,应用更多。计算发现,颗粒尺寸对两相滞后影响很大,在喷管喉部处,颗粒滞后最大。对高凝相浓度喷管两相流,常滞后和任意滞后模型的结果与实际偏差较大,且很难通过模型改进来提高计算精度。因此,这两个模型参考价值不大。但全耦合模型假设少、计算精度高,可用于高凝相浓度喷管两相流计算。
喷管两相流本身很复杂,两相流控制方程中包含的两相相互作用、传热等,使方程求解很困难。因此,解析模型往往不能很好描述实际流动情况,在高精度求解时,需用数值模型代替。
1.2 喷管两相流数值模型的研究
数值模型采用数值方法直接求解两相流控制方程。因此,能完整考虑颗粒的速度和温度滞后,计算结果更准确,但计算量更大。数值模型的使用主要分为三步:(1)在喷管物理模型上,建立适合求解的两相流控制方程、(2)选用合适的数值计算方法、(3)设置合理的求解条件,以进行计算并输出结果。其中,控制方程的建立和计算方法的选定是喷管两相流计算的核心和难点。根据描述颗粒参数的控制方程和求解方法不同,数值模型主要可分为颗粒轨道模型(欧拉-拉格朗日模型)和颗粒拟流体模型(欧拉-欧拉模型)[34]。
1.2.1 颗粒轨道模型
颗粒轨道模型用拉格朗日表达方法描述喷管中的颗粒,并沿颗粒轨道求解其参数,用欧拉方法求解喷管中燃气的参数。
(1)模型方程的处理方法
早期的颗粒轨道模型未考虑颗粒质量、动量及能量的湍流输运,并把模型方程写为欧拉坐标系下的表达式[17]。稳态模型控制方程组在喷管的跨音速段是奇异的,直接求解很困难。为此,研究者们按照方程维度不同进行了许多探索[21,35]。
在一维模型方程下,消除方程奇异性的方法主要有3种:变量置换法、指定压力法和时间相关法[36]。“变量置换法”通过变量替换消除方程的奇异性,“指定压力法”通过选取合适的压强,以减少未知量的个数,从而消除方程的奇异性,并根据流道面积,判断是否收敛[34-35]。一维控制方程求解时,需把喷管分为亚音速段、跨音速段和超音速段,上述两种方法仅限于跨音速段的求解。“时间相关法”在稳态控制方程中引入非稳态项,以消除方程的奇异性,并用准稳态的思想求得稳态喷管两相流场[37-38]。该方法不需对喷管分段,而是对整个喷管求解,相比变量置换法,方程更简单;由于不需反复选取参数,相比指定压力法,计算更容易。因此,在在一维喷管两相流求解中被广泛应用,也被推广到多维问题的求解上。
二维轴对称和三维模型更符合物理实际,应用更多,消除方程奇异性的方法主要有常滞后假设法、数值迭代松弛法、相容条件法和时间相关法。“常滞后假设法”使用常滞后假设,简化求解喷管跨音速段的流场。因此,避免了方程的奇异问题。经实验证明,在该区域使用常滞后模型是合适的[21,39-42]。但由于计算精度低,该方法仅适用于小曲率喷管。“数值迭代松弛法”首先用两相平衡流模型,计算得到喷管初始流场;然后,假定燃气参数不变,计算颗粒参数,再用新的颗粒参数计算新的气相流场,反复迭代直至收敛[43]。该方法也仅用于喷管跨音速段的求解,没有考虑方程的混合型性质。因此,也没有真正让两相全耦合,计算精度很低。“相容条件法”通过引入相容性条件,消除了方程的奇异性,在由流线及其法线所组成的坐标系中,求解控制方程组,假设燃气的流线由初场确定,且不受颗粒的影响[44]。因此,改进了迭代松弛方法,提高了计算精度。上述数值方法由于在每次迭代时,仅计算燃气或颗粒的参数,都是两相非耦合方法。“时间相关法”能消除方程的奇异性,并实现两相全耦合,最早由Chang[37,45]应用在二维轴对称喷管求解上。由于两相耦合程度高,相比前几种方法,其计算精度大大提高,因此应用更广。该方法可对整个喷管和发动机内流场直接求解,且能用于边界复杂的喷管。
由上述讨论可见,“时间相关法”适用于喷管稳态两相流场计算。为了提高计算准确度,还需考虑颗粒湍流对流场的影响。因此,在模型方程中,应包含湍流项。考虑湍流会增加计算的难度,但求解方法不需改变太大。根据方程形式及湍流处理方法不同,轨道模型可分为(有湍流影响的)确定轨道模型和随机轨道模型[17]。
“确定轨道模型”求解的是时均拉格朗日形式的颗粒控制方程,并从拟流体假设中,引入颗粒的漂移速度和漂移力的概念,以考虑湍流扩散对颗粒轨道的影响。“随机轨道模型”直接求解轨道拉格朗日形式的颗粒瞬时控制方程,沿颗粒轨道计算颗粒的湍流参数。
(2)数值计算方法
控制方程的形式确定后,需使用合适的方法求解。在一维模型方程下,时间相关法最终得到一阶非线性常微分方程组,可采用Rugge-Kutta法求解。但二维轴对称和三维模型方程很复杂,只能采用数值积分法求解。气相的数值积分方法与单流体相同,而颗粒的数值方程是拉格朗日形式的控制方程,除颗粒参数外,还需求解颗粒轨道。因此,一般用Rugge-Kutta积分法和线性近似法计算,而在随机轨道模型下,需使用Monte-Carlo法[46-54]。另外,边界条件和数值积分格式对结果准确性的影响也很大。其中,数值格式直接影响计算的精度,研究人员进行了大量的研究[55-56]。
颗粒轨道模型计算量小,能模拟有复杂经历的颗粒,没有伪扩散,但不易考虑颗粒的湍流扩散过程,在复杂流场下,难以给出连续的颗粒参数分布。因此,很难和实验对照。在喷管中,颗粒会经历相变、变形、成长、团聚、破碎、碰撞、沉积、辐射和化学反应等各种情况,用颗粒轨道模型计算时,能清楚反映颗粒变化过程[13,56,57-63]。对高凝相浓度喷管两相流,喷管中颗粒很多,颗粒间会相互干扰,颗粒运动受湍流影响很大,应采用随机轨道模型进行模拟。
1.2.2 颗粒拟流体模型
拟流体模型假设颗粒为拟流体(具有粘性、导热和扩散等流体属性,与气相相互渗透,且占有一定体积分数[64]),模型方程是欧拉形式的颗粒方程和气相方程,能完整考虑滑移、相间耦合和湍流扩散,最终得到连续的颗粒参数分布。
(1)模型方程的处理方法
颗粒拟流体模型求解湍流两相流时均守恒方程组,相比颗粒轨道模型,更完整更严格地模拟气相湍流和颗粒湍流,仍采用时间相关法分析和计算。颗粒湍流在拟流体模型研究中是一个重要概念,包括颗粒与流体的湍流相互作用、颗粒自身的湍流输运(湍流粘性、扩散和导热等)、颗粒间碰撞引起的湍流输运、颗粒质量扩散引起的湍流输运等[17]。拟流体模型中湍流的描述方法来源于单流体湍流模型,后者常用的有两种:涡粘性模型中的双方程模型(如k-ε模型)、雷诺应力模型中的代数应力模型。在拟流体模型研究过程中,以时间相关法为基础,逐步发展了层流气相-层流颗粒的、湍流气相-层流颗粒的以及湍流气相-湍流颗粒的拟流体模型,这些模型曾被用于喷管两相流计算中,但随着计算技术的进步,已逐渐被淘汰[65-73]。最新研究是完整考虑湍流影响的颗粒拟流体模型,最常见的是k-ε-kp-εp四方程湍流模型[73],其他模型也在研究中。这些模型方程应采用合适的数值计算方法求解。
(2)数值计算方法
颗粒拟流体模型方程采用数值积分法求解,可沿用并改进单相流的求解方法,如SIMPLE算法。方程离散方法主要有有限差分法(FDM)、有限体积法(FVM)和有限元法(FEM)。其中,有限体积法以有限差分法为基础,目前大部分数值积分方法都是在有限体积法的基础上发展出来的,这些方法[55]包括用黎曼精确解或近似解求解界面通量的Godunov方法、通过方程中通量的变形而衍生的通量求解方法(如通量分裂求解的Van leer方法和Steger-Warming方法),还有基于流动基本规律的一些积分方法(如总变差不增TVD格式)。在多维模型方程中,界面通量求解很困难,常用矢通量分裂法得到各方向上的一维黎曼算子,用Godunov法求解该方向上的黎曼近似解,最终组合为整个流场的解[56]。合适的数值积分格式能保证计算的完成,目前常用的数值格式包括一阶/二阶迎风格式、混合格式、乘方格式、HLL、AUSM、MUSCL、Lax-Wendroff、NND格式等,近年来有许多数值格式的研究,新的高精度格式不断出现。数值格式在选取时,需保证稳定性、守恒性等法则,应根据实际情况选取。拟流体模型方程的求解需使用TDMA算法、低松弛迭代、源相线性化等手段,与单相流类似。
用时间相关法及合适的数值格式求解控制方程时,需要满足CFL条件:Δt≤Δx/(ug+c),计算才能收敛。为提高计算速度,侯晓等[74]用“隐式近似因子分解法”,在差分格式上做了一些改变,减弱了该条件的影响,当喷管中颗粒较小(Dp<1 μm)时,该方法较适用。另外,喷管流场的边界条件对数值计算结果影响也很大,为了确定合适的喷管入口边界条件,方丁酉提出用虚拟喷管法确定两相混合物的入口速度[36]。
颗粒拟流体模型完整考虑了颗粒的湍流输运,能得到颗粒在流场中连续的速度、温度、体积分数和湍流参数的分布,还能考虑颗粒碰撞引起的颗粒参数的变化,结果易于与实验对照。但该模型不能描述单个颗粒的运动和变化情况,存在伪扩散,当颗粒分组较多时计算量大。对于高凝相浓度喷管两相流,由于颗粒含量高,碰撞可能性大,受湍流影响也很大,要重点考虑这些因素的影响时,用拟流体模型较合适。
上述理论模型都是从不同角度对真实过程进行的简化和近似,两相平衡流模型是较大的简化。实际中,常用的是颗粒轨道模型和颗粒拟流体模型。两者侧重点不同,颗粒轨道模型适用于描述颗粒的详细运动和变化过程,颗粒拟流体模型适用于描述颗粒参数的空间分布。对于高凝相浓度喷管两相流,应按照研究侧重点不同,选择合适的计算方法。
2 喷管两相流实验研究的进展
同一喷管流动过程在不同理论模型或计算方法下得到的结果可能不同,甚至互相矛盾[75]。两相流实验研究的主要目的是验证理论计算结果,用以辅助工程设计。实验研究的手段包括喷管两相流场参数测量、两相相互作用测量、颗粒粒径测量和颗粒动力学特性测量等。随着测量技术的进步,两相流实验研究发展很快。
2.1 喷管两相流场参数的测量
两相流场参数测量实验包括冷流模拟实验和发动机实验两种,前者由于和实际情况差别很大,难以模拟真实的流动状态,而后者对测量技术的要求很高,常规测量方法在高温高速的气固两相喷管流动环境中往往失效。在发动机实验(包括简化或缩比的喷管流动特性实验)中,喷管流场参数的测量方法主要是非接触测量法[76]。该方法以摄影、射线、激光和图像处理技术为基础,包括X射线高速实时荧屏分析(RTR)、粒子图像测速(PIV)、激光多普勒测速(LDV)、高速摄影和重曝摄影等。通常可测得颗粒的分布规律、颗粒速度和轨迹,这些测量结果与理论计算结果比较,可用于验证模型的准确性。
早期研究从两相不平衡角度出发,用消光测量法(Light Extinction Measurements)和钠D-线反转技术(Sodium D-line Reversal Technique),测量了颗粒的速度滞后和温度滞后,证明了滞后效应的存在,并得到了与一维解析模型吻合的结果[77-78]。后来,Neilson等[79]为了验证非耦合模型的计算结果,用重曝摄影法分析了颗粒运动速度,发现非耦合模型仅在颗粒凝相浓度很小时适用。20世纪70~80年代以来,喷管两相流理论计算以颗粒轨道模型和颗粒拟流体模型为主,喷管两相流实验研究主要用于观察扩张段是否存在无颗粒区、颗粒轨迹是否会越过喷管轴线、颗粒运动受重力影响的程度等问题[75-80]。在所有测试方法中,RTR技术不需使用可视喷管,应用最广。对于高凝相浓度喷管两相流,目前理论研究还很不完善,须用合适的实验方法,验证其计算结果。
2.2 两相相互作用实验研究
喷管中颗粒和燃气间相互作用主要是作用力和传热,其中作用力包括颗粒的气动阻力、升力、体积力等,一般情况以阻力为主;两相传热则包括热传导、对流换热和辐射,以对流和辐射为主。为便于计算,在控制方程中用阻力系数CD计算作用力,用Nu数计算对流传热。在均匀无粘低速两相流中,可仅考虑气动阻力和导热,通过理论推导得到CD=24/Re,Nu=2,这2个值又被称为斯托克斯阻力系数和传热系数,用CDs和Nus表示[34]。实际情况比这一情况复杂得多,只能通过实验测量得到CD和Nu数的经验计算式。
(1)两相阻力系数CD的实验测量
标准阻力曲线是测量不可压无限大流场中刚性球体的受力得到的,可用式(2)拟合:
(2)
在实际情况下,阻力系数受许多因素的影响。Bailey等[81]在Ma=0.1~20、Re=0.2~106的参数范围内,测量了颗粒阻力,并得到如下计算式:
(3)
式中 阻力系数的各个修正项依次为雷诺数函数、湍流效应、气相稀薄效应、可压缩性、颗粒非球形修正和温差效应修正。
式(3)考虑得比较全面,但公式形式复杂。目前,在喷管两相流计算中,最常用的是标准阻力曲线,以及Carlson等[82]的经验公式:
(4)
另外,也常使用Hermsen[83]的经验公式:
(5)
其中,CD,inc为由标准阻力曲线拟合的阻力系数,G(Re)和h(Ma)分别为Re数和Ma数的函数。
除了上述公式外,还有许多用于喷管两相流研究的阻力系数计算经验公式,迟鸿伟[14]比较了各个公式,结果发现,Hermsen的公式是可靠的。
对高凝相浓度喷管两相流,颗粒间空隙小,大尺度湍流被分割,气相稀薄效应影响大,阻力系数变大,CD计算式中应引入颗粒浓度影响[84]。另外,颗粒形状不规则,其变化过程也会对阻力系数产生影响[62]。在实验中,完全量化这些因素的影响很困难,Koike等[85-86]用PIV和LDV方法,实验测量了颗粒的运动速度,并分析了颗粒受力,与理论结果比较,对阻力系数经验公式进行了修正。这一方法可推广到高凝相浓度喷管两相流中。
(2)两相传热Nu数的实验测量
在不可压流中的球形颗粒,相间温差较小时,两相传热以对流换热为主,实验测量得到Nu数平均值的经验公式如下:
Nu0=2+0.459Re0.55Pr1/3
(6)
其中,1 为了考虑湍流或稀薄效应的影响,Kavanau等[87]通过实验得到如下经验公式: (7) 该公式在颗粒较多,克努森数Kn≤0.1时适用。 另外,Koshmarov等[88]在整个喷管中得到了Nu数计算公式,Nelson等[89]在高温喷管流动情况下,验证了上述两个经验公式的正确性。 (3)两相辐射的实验测量 在喷管两相流中,辐射传热以颗粒辐射为主,包括颗粒对壁面、燃气的辐射和颗粒间辐射。该问题的求解需要积分光谱辐射传输方程(spectral radiative transfer equation),常用的积分方法是有限体积法[90]。颗粒离散相的辐射特性参数的确定是两相流辐射问题的难点,这些参数很难通过理论分析得到,往往需要通过实验测量,并结合辐射反问题模型反演求解[91]。颗粒辐射特性参数一般是指颗粒的光学常数(复折射率),该参数与温度相关,通过实验和理论求得。实验方法可分为测反射率法、测方向散射率法和测单色透射率光谱法,每种方法的实验结果均可结合相应的理论模型反演计算,最终可求得颗粒复折射率。 发动机喷管中颗粒的温度很高,一般是颗粒对外辐射散热。目前,没有直接测量喷管内高温颗粒辐射的研究,大部分是在炉膛内测得。最初的研究采用傅立叶红外光谱仪(FTIR)和KBr吸收渣片等实验手段,测量了煤粉或炉灰颗粒在高温下的复折射率[92]。齐宏[91]设计并搭建了高温粒子辐射特性测试综合实验平台,通过测量自然状态下Al2O3颗粒的光谱等效透射比,反演得到了颗粒的复折射率。Al2O3颗粒的复折射率与其温度、粒径、浓度等参数相关。在齐宏的实验中,颗粒浓度为6.563×10-5,而在铝冰发动机喷管中,颗粒凝相浓度为17时,浓度约为5.6×10-3。可见,现有实验结果与高凝相浓度喷管两相流实际情况相差仍较大,在求解精度要求不高时,可用于近似计算。 2.3 颗粒粒径的实验测定 颗粒粒径直接影响喷管两相流动状态,并最终影响发动机性能,只能通过实验测得。颗粒团聚和破碎会对粒径产生影响,在不破坏颗粒原本状态的情况下,实验测得的粒径包括单个颗粒的粒径和颗粒团聚物的粒径,统称颗粒粒径。 在简单喷管两相流计算中,颗粒粒径往往采用平均粒径[93],一般用如下经验公式计算[8]: (8) 式中p为喷管头部压强;ξ为颗粒含量;L*为发动机内流场特征长度;Dt为喷管喉径。 实际情况是粒径呈一定规律分布,大小粒径同时存在,仅用平均粒径不足以描述两相流动的实际情况。测量粒径分布的实验方法分为接触测量法和非接触测量法。接触测量法先收集颗粒然后用粒度测定仪、颗粒计数器、电镜观察计数等方法得到粒径分布[94]。颗粒收集方法包括: (1)把收敛喷管和装有惰性冷却液的容器相连,从而收集通过喷管喉部的颗粒[95]。 (2)用冷却容器或冷却喷流法收集喷管出口羽流中的颗粒[94,96-97]。 (3)发动机工作完成后,从喷管壁面残留物中收集颗粒[8]。 前2种方法应用较多,Sehgal[94]系统地研究了推进剂中金属含量及粒径、燃烧室温度、压强、喷管型面、颗粒驻留时间等对喷管出口处颗粒粒径的影响,发现压强是颗粒粒径的主要影响因素。娄永春等[95,98-99]通过改进的颗粒收集装置测量发现,颗粒聚集程度越大,颗粒粒径越大;压强越大,颗粒粒径越大;聚集情况下颗粒粒径分布范围较宽,往往呈双峰或多峰分布,主峰所占比重很大。在高凝相浓度喷管两相流中,颗粒含量高,在整个喷管流动范围内都可称为“颗粒聚集”的状态,上述颗粒粒径分析结果可用于高凝相浓度喷管两相流研究。 非接触测量法用RTR技术、高速摄影、激光衍射等方法,直接获取喷管内或喷管出口的两相流图像/数据,再用计数法、光谱分析等统计方法,分析图像或光谱数据,得到粒径分布情况[100-102]。Koo等[100]总结了各种测量方法的优缺点,把非接触测量法分为无图技术(nonimaging techniques)和有图技术(imaging techniques),有图技术包括摄影、全息摄影和自动图像处理技术,无图技术包括单粒子计数器和光衍射的集成粒径测量技术(Ensemble Particle Sizing Technique)。后者精度更高,适合用于喷管尾流中颗粒粒径的分析。张宏安等[101]用激光全息光学方法,测量了喷管出口颗粒粒径分布曲线,发现喷管出口颗粒粒径比原始金属粒径小,颗粒破碎速率大于团聚速率,颗粒粒径随铝含量增高而增大。Youngborg等[102]用光衍射法和高速摄影法,测量了开窗的端燃发动机喷管入口和出口处颗粒粒径,发现在喷管收敛段内,凝相粒径是以15~19 μm为中心的单峰分布。在喷管出口,颗粒粒径变小,呈多峰分布。非接触测量法目前仍未用于喷管高凝相浓度两相流中颗粒的测量,该方法不影响流场,采用RTR技术能得到喷管内任意位置颗粒粒径,值得进一步研究。 2.4 颗粒动力学特性的研究 在带潜入喷管的发动机中,颗粒会进入喷管背壁区沉积,并形成残渣,极大程度地影响发动机的正常工作,这是两相流研究的重点。用RTR技术可测量颗粒沉积的过程,但分辨率不高,而用冷流模拟可近似地描述颗粒的运动过程。韩新波[103]用冷流模拟和相位多普勒粒子分析仪(PDPA)测速技术,分析了潜入喷管和其背壁区内的两相流动,验证了双流体数值模型。 在有过载的发动机中,颗粒会定向运动,在发动机或喷管局部形成高凝相浓度两相流,最终造成燃烧室或喷管材料的烧蚀。娄永春[95]用收敛喷管聚集形成高浓度两相流,对多层复合材料进行了烧蚀实验,实验后发现,高强度石墨喷管被烧蚀。陈剑等[104]研究了发动机正常工作和过载状态下喷管的烧蚀,验证了颗粒随机轨道模型用于预测喷管烧蚀现象的准确性。在长尾喷管中,颗粒滞留时间长,也很容易造成喷管烧蚀[59]。另一方面,由于难烧蚀喷管喉衬材料的使用,两相流更可能导致颗粒在喷管壁面和喉部的沉积,导致发动机工作性能改变。贾林祥等[105-106]通过总结喷管颗粒沉积层厚度的数据,分析了沉积速率,讨论了颗粒沉积对发动机性能的影响。 在喷管中,颗粒的相变、碰撞、破碎、团聚等过程不仅会影响颗粒粒径和运动状态,也会对气相流动产生影响,最终影响发动机性能。刘丛林[62]研究了氧化铝形成和非稳态相变凝结过程,发现燃烧室内有20%的Al2O3会在铝颗粒表面凝结形成大颗粒,剩余的80%凝结为小液滴(烟雾)。目前,尚未在实验中观察到气态的Al2O3,而一般推进剂的燃烧温度不高于Al2O3的沸点(3 800 K,常压)。因此,可认为喷管内是由惰性燃气和Al2O3颗粒、小液滴组成的两相流。通过喷管时,小液滴由于布朗运动和惯性运动的作用,会向大颗粒表面凝结,这实际上是小颗粒与大颗粒的碰撞。夏胜勇[107]详细研究了氧化铝颗粒的碰撞过程,并指出氧化铝液滴属于高粘度、高表面张力系数的液滴,直接研究颗粒在喷管中的碰撞过程很困难。Averin等[108]用激光诊断方法,对发动机喷管内氧化铝颗粒的碰撞团聚过程进行了测量,验证了其颗粒碰撞模型的正确性。 本文综述了喷管内两相流理论和实验研究的进展,讨论了各种研究方法和研究结果对高凝相浓度喷管两相流研究的参考价值。 理论研究包括解析模型研究和数值模型研究,解析模型中,两相平衡流模型能够用于计算喷管的最大理论工作性能,等温流模型是对高凝相浓度喷管两相流的一种假设,可用于工程计算。数值模型包括颗粒轨道模型和拟流体模型,能完整地考虑两相速度、温度滞后,并计算湍流对两相流动的影响,这2种模型都能用于计算高凝相浓度喷管两相流,并得到较好结果。理论研究是从不同角度对真实两相流动过程的近似和简化,目前仍不完善,还需用实验验证。 喷管两相流的实验研究主要用于理论模型的验证,并可由实验观察得到的一些规律反演出新的理论模型。从目前研究结果看,实验能很好地验证数值计算结果。理论计算所需的颗粒参数,如颗粒粒径、阻力系数和传热等,都是从实验测量得到。因此,实验与理论密不可分。 总之,高凝相浓度喷管两相流研究还很不完善,还需要进一步研究。 [1] 庞维强,樊学忠.金属燃料在固体推进剂中的应用进展[J].化学推进剂与高分子材料,2009,7(2):1-5;14. [2] 庞爱民,黎小平.固体推进剂技术的创新与发展规律[J].含能材料,2015,23(1):3-6. [3] Risha G A,Connell Jr T L.Novel energetic materials for space propulsion[R].Nasa:DTIC Document:A546818,2011. [4] 刘巍.固体燃料冲压发动机燃烧组织技术研究[D].长沙:国防科技大学,2010. [5] Hu J X,Han C.Experimental investigation on combustion of high-metal magnesium-based hydroreactive fuels[J].Journal of Propulsion and Power,2013,29(3):692-698. [6] Farrow D D.A theoretical and experimental comparison of aluminum as an energetic additive in solid rocket motors with thrust stand design[D].University of Tennessee,2011. [7] Geisler R L,Kinkead S A.The relationship between solid propellant formulation variables and motor performance[C〗//11th Propulsion Conference,AIAA 75-1199. [8] Coats D E,Nickerson G R.A computer program for the prediction of solid propellant rocket motor performance[R].CA:Edwards Air Force Base,1981. [9] Wood T D.Feasibility study and demonstration of an aluminum and ice solid propellant[D].Purdue University,2010:227. [10] 张胜敏,胡春波.固体火箭发动机燃烧室凝相颗粒燃烧特性分析[J].固体火箭技术,2010,33(3):256-259. [11] Risha G A,Sabourin J L.Combustion and conversion efficiency of nanoaluminum-water mixtures[J].Combustion Science and Technology,2008,180(12):2127-2142. [12] 杨寒.铝冰固体火箭发动机气固两相流喷管参数研究[D].哈尔滨:哈尔滨工程大学,2013. [13] 胡凡.镁基燃料水冲压发动机理论分析与试验研究[D].长沙:国防科技大学,2008. [14] 迟鸿伟.大负载比气固两相流喷管参数研究及通道形状优化[D].哈尔滨:哈尔滨工程大学,2011. [15] Soo S L.Gas dynamic processes involving suspended solids[J].AIChE Journal,1961,7(3):384-391. [16] Gordon S,Mcbride B J.Computer program for calculation of complex chemical equilibrium compositions and applications[R].Nasa,Cleveland,OH,United States:NASA Lewis Research Center,1994:58. [17] 周力行.湍流两相流动与燃烧的数值模拟[M]. 北京:清华大学出版社,1991:81-164. [18] Dillon P L P.Heat transfer between solid particles and gas in a rocket nozzle[J].Journal of Jet Propulsion,1956,26(12):1091-1097. [19] Gilbert M,Davis L.Velocity lag of particles in linearly accelerated combustion gases[J].Journal of Jet Propulsion,1955,25(1):26-30. [20] Rudinger G.Gas-particle flow in convergent nozzles at high loading ratios[J].AIAA Journal,1970,8(7):1288-1294. [21] Rudinger G.Fundamentals of gas particle flow[M].Elsevier,2012. [22] 王天祥,何利民.气液两相喷嘴等温流动模型[J].机械工程学报,2008,44(1):121-125. [23] Kliegel J R.One dimensional flow of a gas particle system[R].DTIC Document,1959. [24] Kliegel J R.Gas particle nozzle flows[C]//Symposium (International) on Combustion,1963:811-826,0782- 0784. [25] Bailey W S,Nilson E N.Gas particle flow in an axisymmetric nozzle[J].ARS Journal,1961,31(6):793-798. [26] 常显奇.固体火箭发动机燃烧室一维两相常滞后流动[J].宇航学报,1983,4(4):40-52. [27] 常显奇.颗粒尺寸对颗粒速度滞后数的影响[J].推进技术,1985,6(2):1-6. [28] Hassan H A.Exact solutions of gas-particle nozzle flows[J].AIAA Journal,1964,2(2):395-396. [29] Dellinger T C,Hassan H A.Analysis of gas-particle flows in rocket nozzles[J].Journal of Spacecraft and Rockets,1966,3(4):601-603. [30] Ma Y C,Fendell F.Constant-fractional-lag model for axisymmetric two-phase flow[J].Journal of Propulsion and Power,1991,7(5):700-707. [31] Hultberg J A,Soo S L.Metallized propellant and gas-solid suspension flow through nozzle in high energy systems[J].Astronautica Acta,1965,11(3):207-216. [32] 王慧玉,张远君.全耦合的一维两相喷管流的数值解[J].航空动力学报,1986,1(1):53-58;93. [33] Rannie W D.Perturbation analysis of one-dimensional heterogeneous flow in rocket nozzles[M].Progress in Astronautics and Rocketry.1962:117-144. [34] 方丁酉.两相流动力学[M]. 长沙:国防科技大学出版社,1988:187;545. [35] 左罗克,霍夫曼.气体动力学 下册[M]. 北京:国防工业出版社,1984. [36] 方丁酉.一维两相喷管流动[J].宇航学报,1982,3(3):25-40. [37] Chang I S.One-and two-phase nozzle flows[J].AIAA Journal,1980,18(12):1455-1461. [38] Forde M.Quasi-one-dimensional gas/particle nozzle flows with shock[J].AIAA Journal,1986,24(7):1196-1199. [39] Hoffman J D,Conway C C.Analysis of the flow of gas-particle mixtures in two-dimensional and axisymmetric nozzles[R].Dtic:DTIC Document,1962. [40] Kliegel J R,Nickerson G R.Flow of gas-particle mixtures in axially symmetric nozzles[M].Detonation and Two-Phase Flow,1962:173-194. [41] Hoffman J D,Lorenc S A.A parametric study of gas-particle flows in conical nozzles[J].AIAA Journal,1965,3(1):103-106. [42] Kliegel J R,Nickerson G R.Axisymmetric two-phase perfect gas performance program[R].NASA:MSC- 11774,1968. [43] Regan J F,Thompson H D.Two-dimensional analysis of transonic gas-particle flows in axisymmetric nozzles[J].Journal of Spacecraft and Rockets,1971,8(4):346-351. [44] Jacques L J,Seguin J a M.Two dimensional transonic two-phase flow in axisymmetric nozzles[C]//10th Propulsion Conference,1974. [45] Sharma M P,Crowe C T.A novel physico-computational model for quasi one-dimensional gas-particle flows[J].Journal of Fluids Engineering,1978,100(3):343-349. [46] Crowe C T,Sharma M P.The particle-source-in cell (PSI-CELL) model for gas-droplet flows[J].Journal of Fluids Engineering,1977,99(2):325-332. [47] 方丁酉.两相喷管流动研究进展[J].推进技术,1982,3(1):33-42. [48] 方丁酉.两相跨音速喷管流动[J].宇航学报,1987,8(3):43-51. [49] Hayashi A K,Matsuda M.Numerical study on gas-solid two-phase nozzle and jet flows[J].Memoirs of the Faculty of Engineering,Nagoya University,1988,40(2):351-362. [50] 侯晓,何洪庆.固体火箭喷管颗粒尺寸分级两相跨音速流场计算[J].推进技术,1991,12(1):1-8. [51] 侯晓,何洪庆.固体火箭喷管两相粘性跨音速流场计算[J].推进技术,1991,12(2):9-15;25. [52] 陈林泉.固体火箭发动机喷管两相流动计算[J].固体火箭技术,1994,17(1):27-33. [53] 何洪庆,侯晓.在两相粘性跨音速喷管流动中簿层方程的一种隐式求解方法[J].应用数学和力学,1994,15(4):303-312. [54] Hwang C J,Chang G C.Numerical study of gas-particle flow in a solid rocket nozzle[J].AIAA Journal,1988,26(6):682-689. [55] 傅德薰,马延文.计算流体力学[M]. 北京:高等教育出版社,2002. [56] 顾璇.喷管内气粒两相流场的数值模拟[D].哈尔滨:哈尔滨工程大学,2004. [57] Ciucci A,Iaccarino G.Numerical investigation of 3D two-phase turbulent flows in solid rocket motors[C]//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,1998. [58] 昌泽舟,Berlemont A.考虑颗粒间碰撞的气固两相流拉格朗日模拟[J].计算力学学报,2001,18(4):388- 392. [59] 淡林鹏,张振鹏.长尾喷管中粒子运动轨迹的数值模拟[J].航空动力学报,2003,18(2):258-263. [60] 于勇,刘淑艳.固体火箭发动机喷管气固两相流动的数值模拟[J].航空动力学报,2009,24(4):931-937. [61] 杨丹.固体火箭发动机气-固两相流的数值模拟[D].哈尔滨:哈尔滨工程大学,2006. [62] 刘丛林.金属颗粒在气固多相热流场的动力学特性研究[D].哈尔滨:哈尔滨工程大学,2012. [63] 韩超.高金属含量镁基燃料水冲压发动机稳态燃烧机理研究[D].长沙:国防科技大学,2011. [64] Rudinger G.Some effects of finite particle volume on the dynamics of gas-particle mixtures[J].AIAA Journal,1965,3(7):1217-1222. [65] 于勇,张夏.用双流体模型模拟超声速气固两相流动[J].航空动力学报,2010,25(4):800-807. [66] Di Giacinto M,Sabetta F.Two-way coupling effects in dilute gas-particle flows[C]//ASME Winter Annual Meeting 1982,1982:ASME,New York,NY,USA. [67] Coakley T J,Champney J M.Numerical simulation of compressible,turbulent,two-phase flow[C]//18th Fluid Dynamics and Plasmadynamics and Lasers Conference,1985. [68] Mehta R C,Jayachandran T.A fast algorithm to solve viscous two-phase flow in an axisymmetric rocket nozzle[J].International Journal for Numerical Methods in Fluids,1998,26(5):501-517. [69] Perrell E.Two-phase CFD calculations with continuous distributions of particle sizes[C]//34th AIAA/ASME/ SAE/ASEE Joint Propulsion Conference and Exhibit,1998. [70] 高波,叶定友.旋转条件下固体火箭发动机燃烧室气-固两相湍流流动数值模拟[J].固体火箭技术,1999,22(3):6-10. [71] 曾卓雄,姜培正.可压稀相两相流场的数值模拟[J].推进技术,2002,23(2):154-157. [72] Mirzaei M,Shadaram A.Numerical simulation of supersonic gas-particle flow using eulerian-eulerian approach[C]//14th AIAA/AHI International Space Planes and Hypersonics Systems Technologies Conference,November 6,2006:382-389. [73] 王运良,徐忠.气固两相流k-ε-kp-εp双流体模型及应用[J].航空动力学报,1994,9(3):82-84;111. [74] 侯晓,何洪庆.粘性跨音速喷管流场计算[J].推进技术,1990,11(5):11-16;67. [75] 李江,肖育民.固体火箭发动机燃烧室两相流粒子运动轨迹的实验研究[J].西北工业大学学报,1999,17(1):15-18. [76] 肖育民,何国强.用RTR技术研究固体发动机燃烧室中粒子运动轨迹[J].推进技术,1997,15(5):36-45. [77] Carlson D J.Experimental determination of thermal lag in gas-particle nozzle flow[J].AIAA Journal,1962,32(7):1107-1109. [78] Carlson D J.Experimental determination of velocity lag in gas-particle nozzle flows[J].AIAA Journal,1965,3(2):354-357. [79] Neilson J H,Gilchrist A.An analytical and experimental investigation of the velocities of particles entrained by the gas flow in nozzles[J].Journal of Fluid Mechanics,1968,33(1):131-149. [80] 孙敏,方丁酉.二维喷管两相流动实验理论研究[J].航空学报,1988,9(11):572-576. [81] Bailey A B,Hiatt J.Sphere drag coefficients for a broad range of Mach and Reynolds numbers[J].AIAA Journal,1972,10(11):1436-1440. [82] Carlson D J,Hoglund R F.Particle drag and heat transfer in rocket nozzles[J].AIAA Journal,1964,2(11):1980-1984. [83] Hermsen R W.Review of particle drag models[C]//JANAF Performance Standardization Subcommittee 12th Meeting Minutes,1979:113. [84] 周彦煌,孙兴长.气-固两相流中颗粒群的稠密度及粒度对阻力系数影响的研究[J].兵工学报,1984,5(4):11-15. [85] Xiao Y M,Amano R S.Aluminized composite solid propellant particle path in the combustion chamber of a solid rocket motor[C]//Sixth International Conference on Advances in Fluid Mechanics,2006:153-164. [86] Koike S,Takahashi H.Correction method for particle velocimetry data based on the stokes drag law[J].AIAA Journal,2007,45(11):2770-2777. [87] Kavanau L L,Drake Jr R M.Heat transfer from spheres to a rarefied gas in subsonic flow[R].DTIC Report:AD-1911,1953. [88] Koshmarov Y A,Svirshevskii S B.Heat transfer from a sphere in the intermediate dynamics region of a rarefied gas[J].Fluid Dynamics,1972,7(2):343-346. [89] Nelson H F,Fields J C.Heat transfer in two-phase solid-rocket plumes[J].Journal of Spacecraft and Rockets,1996,33(4):494-500. [90] Jung J Y,Brewster M Q.Radiative heat transfer analysis with molten Al2O3dispersion in solid rocket motors[J].Journal of Spacecraft and Rockets,2008,45(5):1021-1030. [91] 齐宏.弥散颗粒辐射反问题的理论与实验研究[D].哈尔滨:哈尔滨工业大学,2008. [92] 李剑云,柳朝晖.求解微粒吸收指数的改进算法[J].工程热物理学报,1996,17(1):116-120. [93] Hermsen R W.Aluminum oxide particle size for solid rocket motor performance prediction[C]//19th Aerospace Sciences Meeting,1981. [94] Sehgal R.An experimental investigation of a gas-particle system[R].DTIC Document,1962. [95] 娄永春.高温稠密两相流冲刷条件下绝热层烧蚀实验研究[D].西安:西北工业大学,2005. [96] 张超才,孙绪全.含铝固体复合推进剂燃气中Al2O3颗粒收集与测量的实验研究[J].推进技术,1986,7(4):56-60. [97] 张胜敏,胡春波.固体火箭发动机喷管喉部凝相颗粒粒度分布实验[J].推进技术,2012,33(2):245-248. [98] 刘洋,何国强.聚集状态下凝相颗粒的收集与测量[J].推进技术,2005,26(5):477-480. [99] 李江,娄永春.聚集状态对固体火箭发动机颗粒粒度分布的影响[J].固体火箭技术,2005,28(4):265-267. [100] Koo J H,Hirleman E D.Review of principles of optical techniques for particle size measurements,in:Progress in Astronautics and Aeronautics[M].AIAA,1996. [101] 张宏安,叶定友.固体发动机喷管出口凝相微粒粒度分布研究[J].固体火箭技术,2001,24(3):14-18. [102] Youngborg E D,Pruitt T E.Light-diffraction particle size measurements in small solid-propellant rockets[J].Journal of Propulsion and Power,1990,6(3):243-249. [103] 韩新波.固体火箭发动机潜入喷管背壁区流动研究[D].西安:西北工业大学,2002. [104] 陈剑,魏祥庚.固体火箭发动机长尾喷管烧蚀实验研究[J].固体火箭技术,2010,33(1):34-35;40. [105] 贾林祥.含铝固体推进剂火箭发动机喷管沉积的实验与传热分析[J].推进技术,1985,6(1):1-10. [106] 赵湘恒,方丁酉.三氧化二铝颗粒在喷管内的沉积[J].固体火箭技术,1988,11(4):55-65. [107] 夏盛勇.三氧化二铝液滴碰撞机理及模型研究[D].西安:西北工业大学,2015. [108] Averin V S,Arkhipov V A.Effect of a sudden change in cross-sectional area of the solid rocket motor duct on coagulation of condensed particles[J].Combustion,Explosion and Shock Waves,2003,39(3):316-322. (编辑:崔贤彬) Research on the high solid concentration two-phase nozzle flow LIU Ping-an,WANG Liang,WANG Lu,WANG Ge,GAO Ye (College of Aerospace and Civil Engineering,Harbin Engineering University,Ha'erbin 150001,China) In order to select proper methods to study the high solid concentration two phase nozzle flow in highly metalized Solid Rocket Motor(SRM),the research advance of two phase flow in rocket nozzles was summarized in two aspects:the theoretical research and the experimental research.Their results and reference value for the high solid concentration nozzle flow research was discussed.It is noticed that the actual two phase nozzle flow lies between the two phase equilibrium flow and the two phase frozen flow.The iso-thermal method is suitable for the primary analysis of the high concentration two phase nozzle flow,as high particle content strengthens the interactions between the particle and the exhaust gas.The numerical methods can be generally categorized in two models:the trajectory model and the pseudo-fluid model,they are both suitable for the simulation of the high solid concentration nozzle flow.The experimental research are mainly used to verify the numerical results,and acquire relevant data for theoretical calculation,such as the particle size distribution,the drag coefficient,and the Nusselt number.The experiment can be greatly simplified if we only study some local features of the particle or the two phase nozzle flow-field,then the results can be expanded to the whole nozzle.By analyzing the research advance of the two phase nozzle flow,the reference for the high solid concentration nozzle flow research was provided. nozzle two phase flow;high solid concentration;solid rocket motor 2016-07-12; 2016-10-09。 中央高校基本科研基金(HEUCFD1404);(HEUCFD1502)。 刘平安( 1980—) ,男,副教授,研究方向为金属燃料发动机。E-mail:liupingan631@126.com V438 A 1006-2793(2016)06-0735-11 10.7673/j.issn.1006-2793.2016.06.0013 结束语

