无线传感器网络中一种改进的加权质心定位算法研究

张 丹, 董雷刚, 李 梓

(大庆师范学院 计算机科学与信息技术学院，黑龙江 大庆 163712)

无线传感器网络中一种改进的加权质心定位算法研究

张 丹, 董雷刚, 李 梓

(大庆师范学院 计算机科学与信息技术学院，黑龙江 大庆 163712)

在无线传感器网络的应用中节点的定位信息是非常重要的。本论文提出一种改进的加权质心算法，该算法是基于平面多边形定点凹凸性原理进行实现的，算法中选择自由传播模型和对数距离路径分布模型来计算无线电波传播过程。改进的质心算法能够提高定位的精度，仿真实验验证了该算法的平均定位误差，仿真实验结果表明，在相同的条件下，该算法的定位精度高于加权质心算法。

无线传感器网络；加权质心定位；节点定位；顶点凹凸性

0 引言

随着微电子技术的迅猛发展，WSN(Wireless Sensor Networks)即无线传感器网络技术得到了很大的增长。它对人们的生产、生活都产生了很大的影响，而且广泛应用在环境、军事、健康医疗、农业、家庭、交通运输和其它商业领域。无线传感器网络中有大量的传感器节点，这些节点体积小、价格低、计算能力低、有限的能源资源，它们被随机地部署在监测区域中。这些传感器节点的位置信息在无线传感器网络中起到了关键的作用，在无线传感器网络中没有位置信息的节点是没有任何意义的。GPS(Global Positioning System) 即全球定位系统是传感器节点获得定位信息的一种非常有效的方法，但是由于GPS的成本高、体积和重量大，如果为每一个传感器节点都配备GPS是不可行的。与此同时，它会使节点的成本大大增加、体积也随之增大。因此近些年，无线传感器网络中节点的定位问题得到了广泛的关注。根据在定位的过程中是否需要测量网络中节点之间的距离将定位算法分为两种，分别是距离相关的定位算法和距离无关的定位算法两种。

根据无线传感器网络中的节点是否知道自身位置分为信标节点和未知节点，信标节点一般是通过人工部署或者GPS定位来获取位置信息的，这种节点在无线传感器网络中的比例较少，它们的作用是帮助未知节点获得位置信息的。未知节点一般是随机部署的，它们的位置信息是未知的，通过信标节点来计算自身的位置信息。计算未知节点位置信息中的距离相关的定位算法通过获得节点之间的距离或者角度信息来进行，这些算法主要有TDOA(Time Difference of Arrival)到达时间差法[1]、AOA(Angle of Arrival)到达角度法[2]、RIPS(Radio Interferometry Positioning System)无线电干涉定位系统和RSSI(Received Signal Strength Indication)接收信号强度指示定位系统。这些算法具有很高的定位精度，但是需要额外的硬件支持来进行精确地测量。距离无关的定位算法不需要知道节点间的绝对距离和角度信息，根据节点之间的连通性信息来实现自身信息的计算。距离无关的定位算法主要有APIT(Approximate Point-in-Triangulation test algorithm)近似三角形内点测试法[3]、DV-Hop算法[4]、Amorphous算法、质心算法。由于基于距离的定位算法的费用高，因此距离无关的定位算法得到广泛的应用。在距离无关的定位算法中，质心算法简单、开销低、易于实现，因此应用比较广泛。然而质心算法的邻居信标节点的密度、一致性和连通度对未知节点的定位精度有很大的影响，因此在本论文中提出一种改进的质心定位算法，该算法无需额外的硬件，可以提高定位的精度。

1 质心定位算法原理

1.1 质心定位算法

质心定位算法是在2000年由N. Bulusu和J. Heidemann提出的，质心定位算法中的未知节点的位置信息是通过网络中的信标节点的位置信息进行计算的。这种算法的过程包括三个阶段，首先无线传感器网络中的未知节点向邻居节点广播定位请求。然后接收到这个请求的信标节点将它们的id以及接收的信号强度发送给未知节点，未知节点根据接收到的信号强度模型，每个节点计算出与邻居节点的距离。最后当未知节点接收道德信息超过3个则可以计算出它自身的未知。

未知节点的坐标通过公式(1)进行计算。

(1)

其中(xestyest)为未知节点的坐标。假设有n个信标节点，它们的坐标分别为(xi，yi)(i=1，2，…，n)，它们分布在未知节点的周围。

质心算法的基本原理图如图1所示。图中黑色圆点为信标节点，白色圆点为未知节点。显而易见，质心算法的原理比较简单，而且比较容易计算。然而当无线传感器网络中节点的连通度低，未知节点周围的信标节点的密度低时，质心算法的定位精度将大大降低。

图1 质心算法原理图

1.2 测距原理

信号在传播的过程中，其强度是随着距离的改变发生变化的，根据这个变化就可以得出信号强度的衰减与传播距离的关系。目前在无线传感器网络中比较常用的模型是传播损耗模型。在无线传感器网络中，节点被分散在开放的空间，所以本文选择自由传播模型和对数距离路径分布模型来计算电波传播过程。自由空间传播损耗模型方程如下：

PL(d0)=32.44+10nlg(d0)+10nlg(f)

(2)

在方程(2)中，d0为参考距离，f为接收信号强度指示系统的信号强度，PL(d0)为距离为d0的接收信号强度损耗，n为损耗因子。由于周围的环境因素，自由空间传播损耗模型将受到建筑、传输公里和障碍物的高度等的影响。因此，对数距离分布模型更具有实用性。对数距离分布模型方程如方程(3)所示。

PL(d)[dB]=PL(d0)+10nlog(d0)+X0

(3)

在方程(3)中，PL(d)指的传播距离为d米的传播损耗；X0为一个平均值为0的高斯随机变量。未知节点接收到的信号强度如方程(4)所示。

RSSI=Psend+Pamplify-PL(d)

(4)

在方程(4)中，Psend为传输功率，Pamplify为天线增益。

2 改进的质心算法

2.1 加权质心定位算法原理

为了提高质心定位算法的定位精度，加权质心定位算法被提出，它的原理如方程(5)所示。

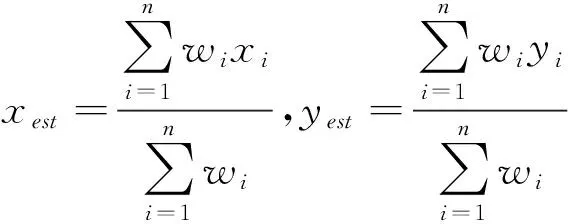
(5)

其中wi为权值，它的值一般可以用方程(6)表示。d是发送者和接收者之间的距离[5]。

(6)

在质心算法中，当未知节点周围的信标节点分布不均匀，定位精度将下降。在本文针对在未知节点周围的邻居信标节点所组成的图形是凸的或者凹的多边形这两种情况，提出了改进的加权质心算法。

2.2 平面多边形定点凹凸性判别

在无线传感器网络中，未知节点周围通信半径内都存在一些信标节点，它们被称为邻居信标节点，这些信标节点通常会构成一个简单的多边形，下面将描述平面多边形顶点凸凹性的原理。

假设未知节点接收到n个信标节点的坐标信息，它们分别是：V1(X1，Y1)，V2(X2，Y2)，…Vn(Xn，Yn)。VA(XA，YA)为距离未知节点最远的邻居信标节点，这个点必然是这些信标节点所组成的多边形的一个凸点。对其余顶点凸凹性的判断可以采用以下原则。取顶点Vi(Xi，Yi)的两个相邻顶点分别为Vi-1，Vi+1，连接点Vi-1和点Vi+1，判断点Vi和A是否在Vi-1Vi+1的同一侧，如果他们是在Vi-1Vi+1的同一个侧面则Vi(Xi，Yi)是凹点，否则是凸点。可以利用表达式(7)判断顶点的凹凸性。

(7)

△>0，A和Vi在Vi-1Vi+1的同一侧，Vi为凹点。△<0，A和Vi不在Vi-1Vi+1的同一侧，Vi为凸点。△=0，A和Vi在Vi-1Vi+1上。

2.3 改进的质心定位算法

假设传感器节点被部署在一个二维平面上，而且所有的节点都是静止的。整个改进质心算法的流程如图2所示。

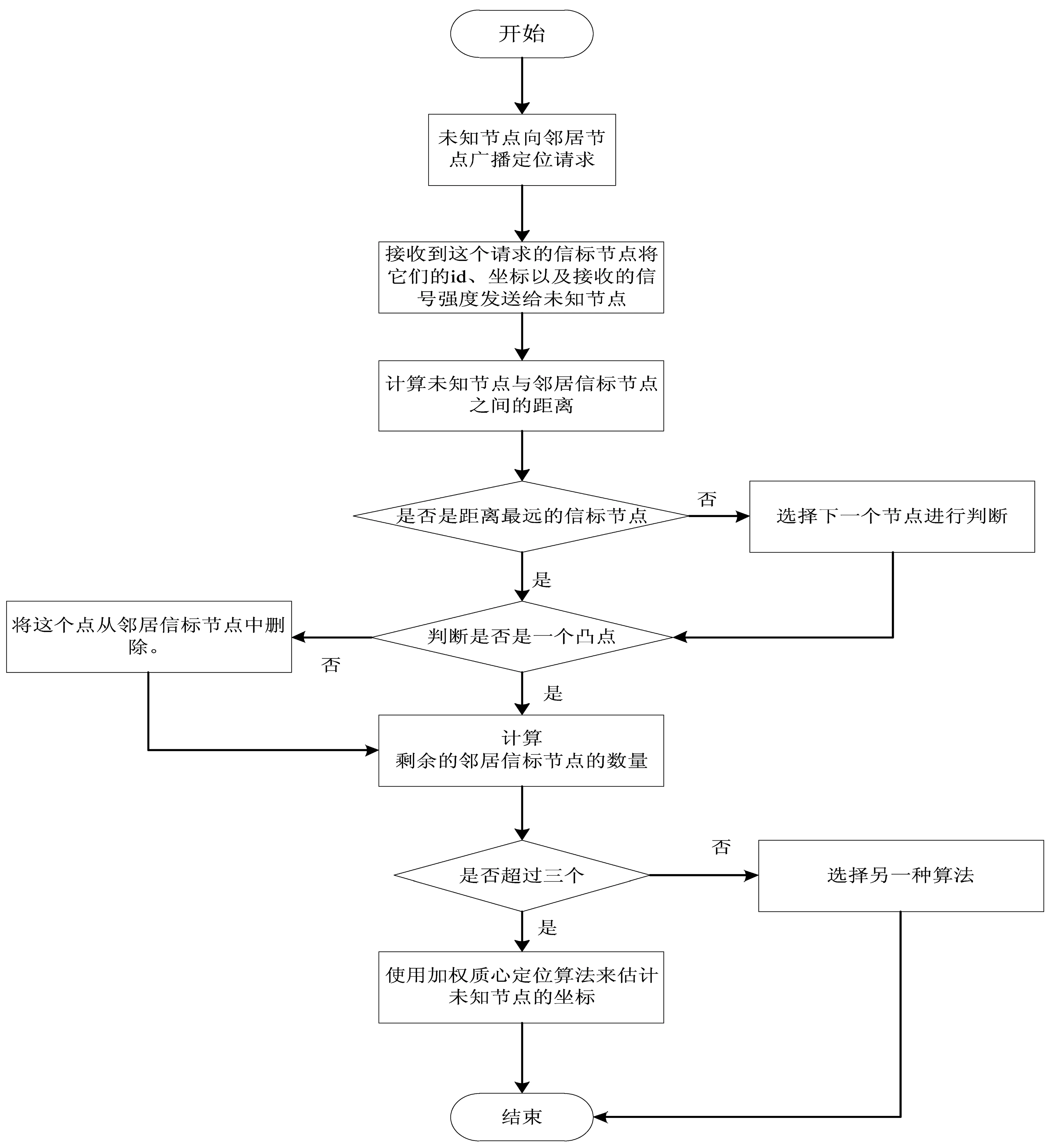
图2 改进质心算法的流程图

无线传感器网络中的未知节点向邻居节点广播定位请求。然后接收到这个请求的信标节点将它们的id、坐标以及接收的信号强度发送给未知节点。计算未知节点与邻居信标节点之间的距离，选择距离未知节点最远的信标节点，该点一定是一个凸点。依次判断每一点是否是一个凸点。如果它是一个凹点，将这个点从邻居信标节点中删除。如果剩余的邻居信标节点的数量超过三个，则使用加权质心定位算法来估计未知节点的坐标。否则，将选择另一种算法。

3 算法仿真实验结论

为了比较改进的质心算法和加权质心算法的效率，进行了仿真，并对实验结果进行了分析。假定有100个传感器节点随机分布在100米×100米的区域，信标节点的比例可根据网络通信连通性进行调整。仿真是在MATLAB 2012中进行的，实验中说明了当信标节点密度为5%和10%两种情况下节点的定位精度，信标节点密度为5%时节点的定位精度小于信标节点密度为10%的定位精度。但是当信标节点密度相同时，本文提出的加权质心定位算法的定位精度明显高于传统的质心定位算法，改进的质心定位算法比加权质心定位算法更精确、更有效。这两种算法的定位精度与网络中的信标节点密度密切相关。当信标定密度增大时，两种算法的定位误差都会减小。因此，本文所提出的定位算法具有一定的实用意义。

4 结 语

在本文中，提出了一种改进的加权质心定位算法，此算法是基于无线传感器网络的平面多边形顶点凹凸性原理进行实现的。在分析无线电波传播损耗模型的基础上，选择自由传播模型和对数距离路径分布模型来计算无线电波传播过程。定位精度通过由未知节点周围的邻居信标节点组成的平面多边形的顶点凸凹性的原则来改进质心算法。仿真实验验证了该算法的平均定位误差的效果，仿真结果表明，改进后的算法比加权质心定位算法更有效。而且网络中的信标节点的密度越高，定位误差越小。

[1] Ergut S，Rao R R，Dural O，et al．Localization via TDOA in a UWB Sensor Network using Neural Networks[J]．IEEE International Conference on Communications，2008：2398- 2403．

[2] Lee YS，Park JW，Barolli L．A localization algorithm based on AOA for ad-hoc sensor networks[J]．Mobile Information Systems，2012，8(8)：61-72．

[3] Yong Zhou，Xin Ao，Shixiong Xia．An Improved APIT Node Self-localization Algorithm in WSN[J]．World Congress on Intelligent Control & Automation，2008：7582-7586．

[4] Tomic S，Mezei I．Improved DV-Hop localization algorithm for wireless sensor networks[J]．IEEE Jubilee International Symposium on Intelligent Systems and Informatics．2012，62(6) ：389-394．

[5] Dong Q，Xu X．A Novel Weighted Centroid Localization Algorithm Based on RSSI for an Outdoor Environment[J]．Journal of Communications，2014，9(9)：279-285．

[责任编辑：崔海瑛]

(英文摘要略)

Research on an improved weighted centroid localization algorithm in wireless sensor networks

Zhang Dan, Dong Lei-gang, Li Zi

(Computer Science and Information Technology DepartmentDaqing Normal University, Daqing 163712, China)

张丹(1979-)，女，黑龙江大庆人，副教授，从事嵌入式系统设计方向研究。

大庆师范学院青年基金项目“基于互联网+人脸识别技术的学生身份认定系统”(15ZR07)。

TP302.1

A

2095-0063(2016)06-0033-04

2016-07-14

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.06.009