解绝对值方程的广义信赖域算法
盛 洲,袁功林,冀祥麟
(广西大学数学与信息科学学院, 广西南宁530004)
解绝对值方程的广义信赖域算法
盛 洲,袁功林,冀祥麟
(广西大学数学与信息科学学院, 广西南宁530004)

绝对值方程;信赖域算法;广义Jacobian矩阵;全局收敛性
0 引 言
考虑具有如下形式的一类绝对值方程(absolute value equations, AVE):

(1)
其中
且A,b为给定的已知常量矩阵或向量。
一般地,式(1)按照矩阵的计算原则化简,可得到:
其中,n为分量的个数,fi(x1,x2,…,xn)为化简后矩阵的分量,i=1,2,…,n。即绝对值方程等价于下列形式的非线性方程组:

(2)
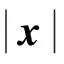
g(x)=diag(sign(x)),

绝对值方程是由Rohn在文献[3]中首次提出的,并且讨论了式(1)的解的存在性和唯一性[4],随后有许多学者对该问题进行了研究。Mangasarian在文献[5]中证明了AVE的求解是一个不可微的NP-hard的优化问题。在文献[6]中,Mangasarian证明了式(1)与线性互补问题等价,线性互补问题是应用科学和工程中一类重要的问题。陈玥琪[7]提出的用光滑牛顿算法求解绝对值方程;Wang等[8]提出的求解绝对值方程的区间算法;雍龙泉等[9]的拟牛顿算法求解绝对值方程;Mangasarian在文献[10]和文献[11]分别提出广义牛顿法和通过凹极小化优化求解绝对值方程;Yong[12]提出了一个迭代算法,通过有限次迭代得到绝对值方程的近似解;Zhang等[13]证明了求解绝对值方程的广义牛顿法的全局收敛性;在文献[14]中,Caccetta等提出了一个具有全局收敛性和二次收敛速率的光滑牛顿法求解绝对值方程。更多求解绝对值方程的方法参见文献[15]~文献[19]。
信赖域方法最早由Powell[20]提出,由于其具有强收敛性和稳定性等优点,在求解非线性优化问题中已经被证明是十分有效的方法之一。对于求解非线性方程组问题,Yuan[21]证明了信赖域算法具有全局收敛性,信赖域算法在非线性方程组问题中应用分析见文献[22]~文献[25]。贯穿全文,‖·‖表示欧几里得范数。
1 信赖域算法
首先,根据文献[6]中性质3和性质4,给出一些绝对值方程的基本结论。
引理1 ①若A∈Rn×Rn,且A的所有奇异值都大于1,则对任意的b∈Rn,绝对值方程存在唯一解;
②若A∈Rn×Rn,且‖A-1‖<1,则对任意的b∈Rn,绝对值方程存在唯一解。
引理2 若A∈Rn×Rn,且A的所有奇异值都大于1,那么对于任意的对角元素是1或-1或0的g,A-g都是可逆的。
对于非线性方程组问题(2),将其转化为一个与之等价的无约束优化问题来求解,即:
(3)
对于信赖域方法,在每个迭代点xk,通过求解下列信赖域子问题得到试探步dk:
(4)
其中Fk=F(xk),Jk=J(xk),Δk是信赖域半径。
若dk由信赖域子问题(4)确定,定义实际下降量和预测下降量分别为:
aredk:=φ(xk)-φ(xk+dk),
(5)
predk:=mk(0)-mk(dk),
(6)
其比值为:
(7)
现在,给出求解非线性方程组问题(2)的广义信赖域算法:
Step 1: 设定初始值,x0∈Rn,0 Step 3: 求解信赖域子问题(4)得到dk; Step 4: 通过式(5)~式(7)分别求出aredk,predk,rk,通过下列准则更新信赖域半径: Step 5: 若rk≥c1,则xk+1:=xk+dk,返回到step 2,令k:=k+1;否则,令xk+1:=xk,返回至step 3,令k:=k+1。 广义信赖域算法的适定性证明类似于文献[26]的定理29及推论3,此处省略不证。 引理3 设{xk}是广义信赖域算法产生的迭代序列,dk是信赖域子问题(4)的解,则{φk}是单调非增的且算法是适定的。 本文做如下假设分析广义信赖域算法的收敛性。 假设1F(x)的所有广义Jacobian矩阵是一致有界的,即∃M>0满足: ‖Jk‖≤M, ∀k∈N+. 假设2 若x*是广义信赖域算法产生点列{xk}的聚点,J(x*)是非退化的。 引理4 若假设1成立,则: 定理1 若假设1和假设2成立,点列{xk}是算法1产生的。那么,算法1经过有限次迭代终止或: (8) 成立。 证明 注意到引理2,假设1和假设2,若: (9) 为了证明式(9)成立,本文采用反证法。假设广义信赖域算法不能有限终止且式(9)不成立,则存在ε>0和无穷多个k满足: (10) (11) 因此: (12)式(12)表明,当k充分大时,有Δk+1≥Δk。这与式(11)矛盾,由此说明式(10)不成立,定理的结论成立。 本文在引理1的前提下,随机生成绝对值方程问题,测试本文广义Jacobian信赖域方法对求解绝对值方程的有效性。本节实验的所有代码都在CPU为Intel Pentium(R) Dual-Core E5800 3.20 GHz, SDRAM为2.00G bytes的Windows7的操作系统下,使用Matlab R2010b运行测试。实验中,算法1中的参数选择为c1=0.1,c2=0.9,α1=0.25,α2=3,ε=10-10和Δ0=1,初始迭代点x0=rand(n,1),其中n为问题维数。 实验中,采用文献[27]随机生成绝对值方程的代码生成n维的随机算例。实验的终止条件为‖F(x)‖≤ε或k≥20(n+1),其中k为算法1的迭代次数。对于信赖域子问题,本文使用Steihaug-Toint方法[28]获得广义信赖域每次迭代信赖域子问题的试探步dk。在实验中,随机生成并测试了维数分别n=100,300,500,800,1 000,1 500,2 000的绝对值方程。实验结果见表1,表1中n表示问题维数;k表示广义信赖域算法求解问题所需的迭代次数;cput表示求解问题所需时间;tfinal表示求解问题的最优值。 从表1中可以看出,广义信赖域算法可以成功地求解绝对值方程维数n≤2 000的问题,所需的迭代次数都比较小,得到的最优值也十分接近于0。但同时,也不难发现,对于维数n≥500的绝对值方程问题,广义信赖域算法成功求解问题所耗费的时间是比较大的,这是由于在求解信赖域子问题(4)时,需要用到广义Jacobian矩阵的信息,然而广义Jacobian矩阵是n×n维,因此会耗费更多的CPU时间。图1给出了对于表1中不同维数的7个绝对值方程问题的φ(x)的值随迭代次数变化的折线图。总之,由表1和图1可知,对于求解绝对值方程问题,广义信赖域算法是合适的。 表1 数值结果 nkcputtfinal1001088921e-0135698e-133001135303e+0132477e-125001119912e+0277233e-128001199799e+0275561e-1110001127542e+0322458e-1115001214441e+0485761e-1120001458004e+0494748e-11 图1φ(x)的值随迭代次数k的变化图 (责任编辑 梁碧芬) A generalized trust region algorithm for absolute value equations SHENG Zhou,YUAN Gong-lin,JI Xiang-lin (College of Mathematics and Information Science, Guangxi University, Nanning 530004, China) Absolute value equations is a non-differentiable NP-hard problem. In this paper, a trust region algorithm with generalized Jacobian matrix of |x| based on a subgradient is proposed. Under mild conditions, the well-definedness and global convergence of the presented algorithm are proved. The numerical results indicate that the proposed algorithm is very effective for solving absolute value equations (with a maximum dimension of 2 000). absolute value equations; trust region algorithm; generalized Jacobian matrix; global convergence 2016-05-20; 2016-07-22 国家自然科学基金资助项目(11261006);广西杰出青年科学基金资助项目(2015GXNSFGA139001) 袁功林(1976—), 男,河南商丘人,广西大学教授,博士生导师;E-mail:yuangl0417@126.com。 盛洲,袁功林,冀祥麟.解绝对值方程的广义信赖域算法[J].广西大学学报(自然科学版),2016,41(6):2078-2083. 10.13624/j.cnki.issn.1001-7445.2016.2078 O224 A 1001-7445(2016)06-2078-062 广义信赖域算法收敛性


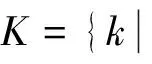


3 数值实验
Tab.1 Numerical results

Fig.1 Values ofφ(x) with the number of iterations4 结 语



