高精度多通信半径DV-Hop定位算法*

孟雯雯，赵建平，马淑丽

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

高精度多通信半径DV-Hop定位算法*

孟雯雯，赵建平，马淑丽

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

无线传感器网络（WSN）中，DV-Hop算法一般应用于粗精度定位。为了进一步减小基于无需测距DV-Hop算法的定位误差，从三个方面依次提出三种呈现递进改进关系的基于多通信半径的高精度DV-Hop改进算法。第一种，通过改变计算跳数值方式，改进多通信半径DV-Hop算法；第二种，在改进的多通信半径算法基础上，改进计算锚节点平均每跳距离的公式；第三种，基于第二种算法，对锚节点平均每一跳距离进行加权处理，使校正值的大小受锚节点与未知节点间的距离影响。MATLAB仿真实验表明，改进的三种算法可以大大提升DV-Hop算法的定位精度。

WSN;节点定位;多通信半径DV-Hop;加权DV-Hop

0 引 言

无线传感器网络（Wireless Sensor Network）中分布着许多微型传感器[1]，每个传感器可以进行信息采集、计算、传输和存储等。在一些军事应用[2]、森林防火、核辐射监测等人类不会长久滞留的地方，传感器节点是由飞机或导弹随机向监测区域抛撒布置的。在一些需要有跟踪服务的应用中，需要知道节点的位置坐标。可见，节点定位技术非常关键[3]。然而，由于成本等原因，只有少数传感器节点装备有GPS或者北斗导航设备[3]。这类节点可以知道自身位置，称为锚节点。大多数节点不知道自身位置，要依靠锚节点的信息计算自己的位置，这类节点称为未知节点。

目前，节点定位技术分为两大类[1,4-5]。一类是基于测距的定位技术，其定位精度高是以牺牲额外的硬件成本为代价的，从而保证未知节点和锚节点之间的距离或角度[5]是精确的，如RSSI定位技术[6]。另一类是基于无需测距的节点定位技术，即只是依靠锚节点的位置信息和节点之间的跳数信息等获得未知节点的坐标，定位精度低，传感器节点不需要额外的硬件设备。在一些粗精度定位中，定位精度满足0.4以下即可。所以，基于无需测距的定位广泛应用在粗精度定位中[6]。其中，DV-Hop算法是典型的基于无需测距的节点定位算法。由于其实现简单方便，所以应用广泛[2]。

只利用节点间传输信息和跳数值计算坐标[7]，DV-Hop算法定位的坐标误差比较大。通信半径、锚节点平均每跳距离、未知节点校正值的选取、锚节点部署方式等条件都能影响节点的定位精度。本文主要从三个方面改进算法，提出三种新的高定位精度DV-Hop算法。三种方法的定位精度呈现递升关系。第一种方法是改进的多通信半径DV-Hop算法，用NRDV-Hop表示。第二种方法是在NRDVHop算法基础上，改进锚节点计算平均每跳距离的公式，用Best-NRDV-Hop表示。第三种方法在Best-NRDV-Hop算法基础上，使用加权概念，在未知节点选择和计算校正值时，对锚节点平均每一跳距离进行加权处理，然后累加得到校正值。第三种方法比前两种方法可进一步减小定位坐标的误差，也是本文最终的高精度定位算法。

本文的结构安排如下。第一部分，定位技术的基础概述，包括DV-Hop算法实现步骤、误差分析及其他文献提出的改进方法介绍。第二部分，本文改进的DV-Hop三种算法，包括改进的多通信半径DV-Hop算法、改进的基于最佳指数的多通信半径DV-Hop算法、改进的基于最佳指数加权的高精度多通信半径DV-Hop定位算法。第三部分，试验验证和分析，共分五个小结验证本文算法的优越性。第一小结仿真和验证本文改进的多通信半径DVHop算法；第二小节求本文改进的高精度算法的最佳指数值；第三小节，实验验证本文改进算法在一定的锚节点覆盖率下，不同的通信半径下的定位优越性；第四小结，验证本文改进算法在不同的锚节点覆盖率、不同通信半径下定位的优越性；第五小节，实验仿真本文算法定位精度的规律与通信半径个数的关系。最后总结文章主旨。

1 基础概述

1.1 DV-Hop算法

DV-Hop定位算法是D. Niculescu 和B. Nath等人提出的六种分布式算法之一[3,8-9]。

假设前提：网络中锚节点与未知节点都随机分布，且有相同的通信半径；通信范围是以自身为圆点的圆；节点间可以互相通信，即具有接收和发送信息的功能；每个节点还具有计算、存储功能。

DV-Hop算法包括以下六个步骤[2-3,10-11]：

（1）锚节点以泛洪的模式向网络发送包含自身坐标信息和初始跳数值0的数据包。

（2）节点接收数据包并保存，将跳数值加1后转发。多次转发过程中，接收节点只接受同一个锚节点较小的跳数值。最终，网络中所有节点已知与其他节点间的跳数值和锚节点位置。

（3）锚节点根据其他锚节点坐标，可以得出与其他锚节点间的距离。然后，根据保存的与其他锚节点间的最小跳数值，计算平均跳距，并作为校正值，向网络第二次泛洪广播。

一般，平均跳距根据无偏估计准则计算，需满足：

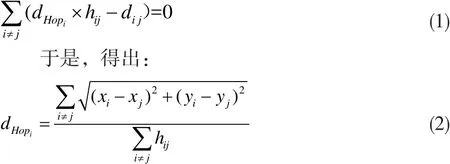
（4）未知节点接收并保存离自己最近的锚节点校正值，即只接收第一个送达的锚节点校正值。

（5）未知节点根据保存的与锚节点间的最小跳数值和接收到的平均每一跳距离（校正值），计算出与每个锚节点的估算距离，见式（3）。

（6）获得至少3个锚节点的计算距离时，用极大似然法、最小二乘法、多边测量法等方法估算自身坐标。

以最小二乘法为例。为了使节点定位误差降到最低，需满足下式：

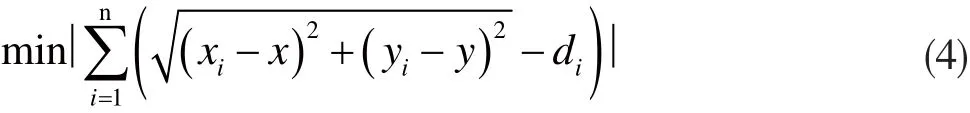
式中，n是锚节点个数，x、y是未知节点真实坐标值，di是未知节点与锚节点i间的估算距离。根据以下式子，利用最小二乘法最终估算出未知节点坐标：

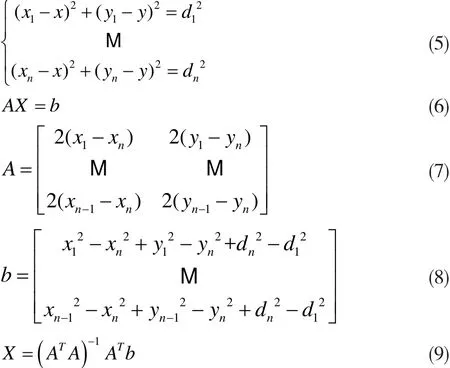
其中，di是定位节点与锚节点i间的计算距离，n是锚节点个数，x、y是定位节点的坐标。

1.2 DV-Hop算法误差分析

只是利用锚节点坐标信息和信息传输的跳数值定位，节点真实坐标与定位坐标之间误差很大[12]。

如图1所示[13]，无线传感器网络部署有三个锚节点A、B、C，其他节点为需要定位的未知节点。用上文公式计算，得为锚节点B的平均每跳距离。可见，得到的锚节点B的平均每跳距离要小于实际的平均跳距[14]，误差较大。此外，锚节点B到锚节点A、C的每一跳距离长短不一，每两跳段间都有角度（非180度），所以用直线距离代替折段距离，求得校正值，误差很大。未知节点用校正值乘以最小跳数值估算与锚节点间的距离，导致估算距离误差大，最终影响定位结果的精确度。

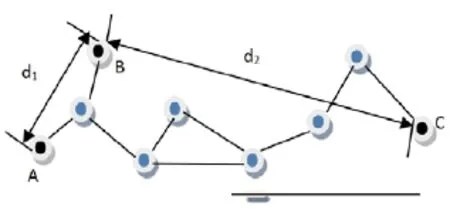
图1 网络结构

1.3 其他文献的改进方法

许多文献从改进锚节点计算平均每一跳公式和锚节点部署方式等改进算法[5,15]，本节主要简单介绍和分析文献[16-19]提出的改进方法。

为了得到更精确的跳数值，文献[16-17]提出在计算平均每一跳距离时可以考虑锚节点用多个通信半径。以2通信半径为例，如图2所示。D、E、F为锚节点，a、b、c、d、e为未知节点，通信半径为R。锚节点D与未知节点a、b的距离分别为R、0.5R，锚节点E与未知节点b、c的距离都为0.5R。如果用一般的DV-Hop算法，锚节点D向未知节点a、b发送信息时，跳数值都加1。锚节点E向未知节点b、c发信息时跳数值是1。假如锚节点有两个通信半径分别为R、R/2，则当使用R/2通信半径时，节点D与b间的跳数值可以为0.5，节点E与b、c间跳数值可以为0.5。这样基于2通信半径的DV-Hop算法得到的跳数值更精确。

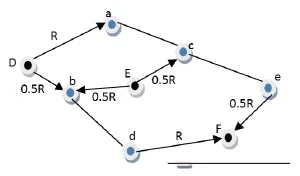
图2 网络结构

然而，文献[16-17]提出的多通信半径算法存在缺陷：在第二次及以后的泛洪中，若发送节点为未知节点，接收节点为锚节点，则未知节点到其一跳范围内的锚节点间的跳数值记为1。如果未知节点到锚节点的距离为R/2范围内，跳数值仍记1，则导致计算平均每一跳距离时的误差很大。如图2所示，未知节点d、e向锚节点F发送信息，跳数值都加1，而未知节点d、e与锚节点F间距离分别为R、R/2。所以，文献[16-17]算法只是将第一次泛洪时锚节点到未知节点的跳数值记为0.5或1，没有考虑转播过程中的精化跳数值。

文献[18-19]证明利用最小均方差准则比利用无偏估计准则定位的坐标误差要高，提出可以考虑用基于最小均方误差准则计算平均跳距，但需满足：

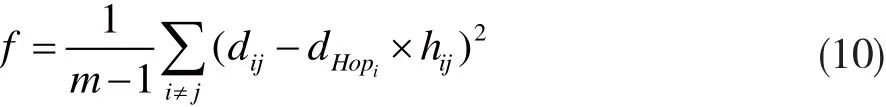
m为锚节点个数，对上式求偏导（对dHopi），然后取零，得：

文献[18-19]只是利用与未知节点最近的锚节点平均每一跳距离作为校正值，却没有考虑其他锚节点的平均每一跳距离，且计算的锚节点平均每跳距离仍然有一定的误差。

以上改进的DV-Hop算法虽然都有缺点，但是比DV-Hop算法都大大提高了定位精度。本文结合上述文献做进一步改进。

2 基于最佳指数加权多通信半径DV-Hop算法

基于1.3节中描述的改进DV-Hop算法，这里将做进一步改进。提出三种改进算法，分别命名为NRDV-Hop算法、Best-NRDV-Hop算法、Weight-Best-NRDV-Hop算法。

2.1 NRDV-Hop算法

NRDV-Hop算法即本文提出的改进的多通信半径DV-Hop算法。多通信半径是指锚节点在每个固定的时间段使用不同的通信半径，通过延时发送信息[20]。多通信半径的DV-Hop算法的前提条件：锚节点可以有多个通信半径值，具有延时功能；网络中未知节点通信半径值只有一个且相同；所有的传感器节点具有接收和发送信息功能。

一般，锚节点最大通信半径与未知节点的通信半径相同，多个通信半径DV-Hop算法在第一步到第n步间，锚节点发送的跳数值ei和通信半径Ri根据式（12）得到。

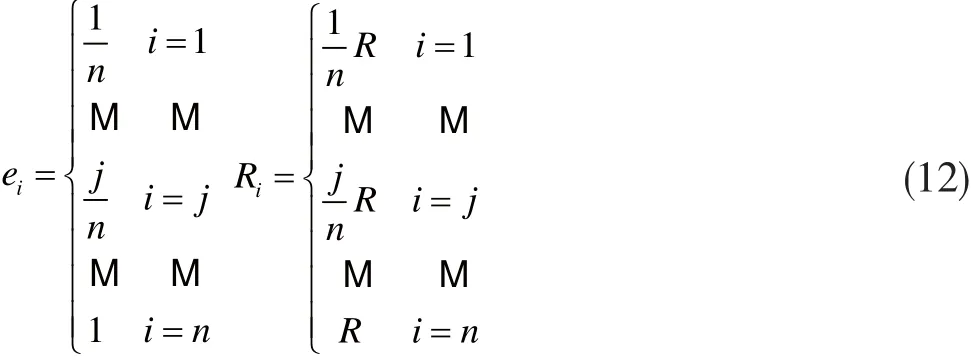
n通信半径的DV-Hop定位算法步骤：

第一步：计时开始，锚节点以通信半径1R向网络广播数据包，内容包括锚节点坐标、编号、跳数等信息。接收节点保留数据包，并单独记录与自己R/n距离内的锚节点的编号，不转发。

第二步：锚节点传输信息和接收节点保留信息所需要的时间假设为t。计时t后清零，重新计时，网络第二次广播数据包，此次广播的跳数值用e2表示，通信半径用R2表示。如果接收节点在第一步中没有接收到任何信息，则保留此次数据并不转发信息，并单独记录与自己2R/n距离内的锚节点的编号。如果第一步已经接收了某锚节点的信息，则抛弃。

接下来，第三步、第四步、…、第(n-1)步都和第一步、第二步相似。在第j次泛洪中，接收节点如果在前几步都没有接收信息，则保留并不转发信息，同时单独记录与自己j×R/n距离内的锚节点的编号；如果在前几步已经接收了某锚节点的信息，则抛弃。经过前(n-1)步，锚节点不同时间段向网络分别以通信半径R1、R2、…、R1-n广播信息，跳数值分别用e1、e2、…、e1-n表示。

第n步：结束计时，最后一次锚节点向网络泛洪广播信息，跳数值取1，通信半径取R。如果接收节点在前(n-1)步已经接收，则抛弃某锚节点信息；否则，接收保留，并将跳数值加1后，向其他节点以通信半径R转发。转播过程中，在第j次泛洪接收节点转播信息时，将锚节点的编号信息也转播。如果接收节点为编号对应的锚节点，该锚节点转播信息时，将跳数值加后转播。最后，网络中全部节点间的最小跳数公开已知，锚节点间也相互知道各自的坐标。

第n+1步：用式（2）计算锚节点的平均每一跳距离，并将其广播出去。离未知节点最近的锚节点平均跳距才能被接受，并作为未知节点的校正值。

最后一步：利用式（3），根据校正值和最小跳数，求未知节点到每个锚节点间的距离。当得到超过三个以上锚节点距离时，未知节点可执行三边测量法、最小二乘等，计算自身坐标。

2.2 Best-NRDV-Hop算法

在NRDV-Hop算法基础上，提出本文第二种改进算法。其他的定位步骤与NRDV-Hop算法一样，但是在求锚节点的平均每一跳距离时，本文在最佳指数值α下求锚节点求平均每一跳距离，以降低误差、提高定位精高度。改进的平均每一跳距离公式如式（13）所示。

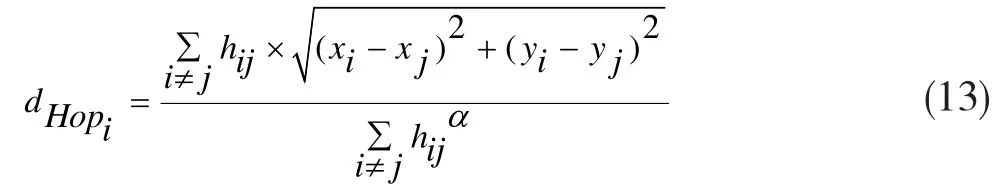
经多次仿真实验发现，α取值为2时，平均每一跳距离的误差不是最小；当精确到0.01时，可以有更佳的α值。多次试验发现，不同的通信半径和锚节点覆盖率等，都会影响最佳α的取值，但是一般α的取值范围不会超出1.88～2.10。

2.3 Weight-Best-NRDV-Hop算法

一般文献选择校正值是将离未知节点最近的锚节点的平均跳距作为校正值。文献[1-2]用未知节点周围所有锚节点平均跳距的平均值作为校正值，但是提升的定位精度并不显然。文献[16]提出基于多通信半径的加权DV-Hop算法。本文结合上述文献的创新思想，将本文Best-NRDV-Hop算法进一步改进，提出第三种改进算法，用Weight-Best-NRDV-Hop表示（基于最佳指数加权的多通信半径DV-Hop）。

其他定位步骤与Best-NRDV-Hop算法一样，只在未知节点选择和计算校正值时，改进未知节点选择校正值的方法。求节点i的校正值时，首先通过式（13）求得锚节点p的平均跳距，接着将跳距乘以一个加权系数XSip。这个系数如式（14），可以体现出未知节点i与锚节点p间的跳数值大小。

将全部被加权的锚节点平均跳距累加[21]，如式（15），未知节点将累加值选作自己的校正值JZi。

最后如式（16），求未知节点i与其他锚节点间的估算距离：将未知节点i的校正值乘以与其他锚节点间的跳数值。

3 MATLAB实验验证

绝对误差[22-23]，即节点的定位误差，指未知节点i的定位坐标(xi,yi)与实际坐标(x0i,y0i)的距离，如式（17）所示。

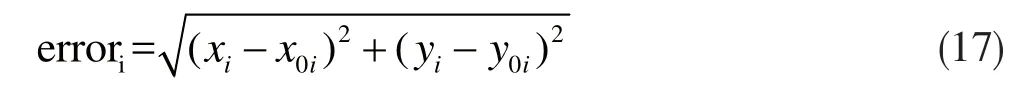
定位精度[22]（Accuracy），计算如式（18）所示，指网络中全部节点（N个）的平均定位误差与节点通信半径R的比值。值越小，说明定位精度越高。

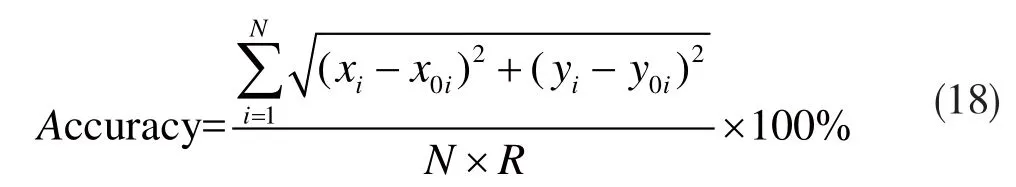
这里，（xi,yi）、（x0i,y0i）分别指未知节点i的定位坐标与实际坐标。

假设网络区域为100 m变长的正方形，随机部署100个节点，如图3所示。为了方便仿真，首先仿真基于2、3通信半径的改进算法，最后仿真基于多通信半径改进算法，即Weight-Best-NRDVHop 算法（N=2,3,4,5,6）。由于节点分布随机性，每个程序仿真100次。

图3 锚节点和未知节点分布图m=9

3.1 2RDV-Hop算法和3RDV-Hop算法

通信半径取20、30、40、50 m，锚节点覆盖率4%～49%，仿真一般DV-Hop算法、一般2、3通信半径DV-Hop算法，并与本文2RDV-Hop算法和3RDV-Hop算法对比，结果如图4所示。

在不同锚节点覆盖率和通信半径下，本文2RDV-Hop算法、3RDV-Hop算法比其他算法占优势。通信半径为30 m、锚节点覆盖率为16%时，本文2RDV-Hop算法和3RDV-Hop算法比DVHop算法分别提高定位精度10.35%、13.5%，本文2RDV-Hop算法比一般2RDV-Hop算法定位精度提高1.22%。本文3RDV-Hop算法比一般3DV-Hop算法定位精度提高1.41%

3.2 求最佳指数值

取通信半径为20、25、30、35、40、45、50 m，锚节点覆盖率9%。将Best-2RDV-Hop算法和Best-3RDV-Hop算法用式（15）求锚节点平均每一跳距离。取不同的α值，找出使Best-2RDVHop算法和Best-3RDV-Hop算法的定位精度最高时的α（此值作为最佳值）值。相同的通信半径条件下，随着指数值从1.9到2.1逐渐增大，定位精度的变化是先提升后降低，如图5（a）、图5（b）所示。Best-2RDV-Hop算法对应的通信半径最佳指数分别为2.01、2.01、2.00、1.99、1.98、1.96、1.95。Best-3RDV-Hop算法对应的通信半径最佳指数分别为2.02、2.02、2.01、2.01、2.00、2.00、1.98。

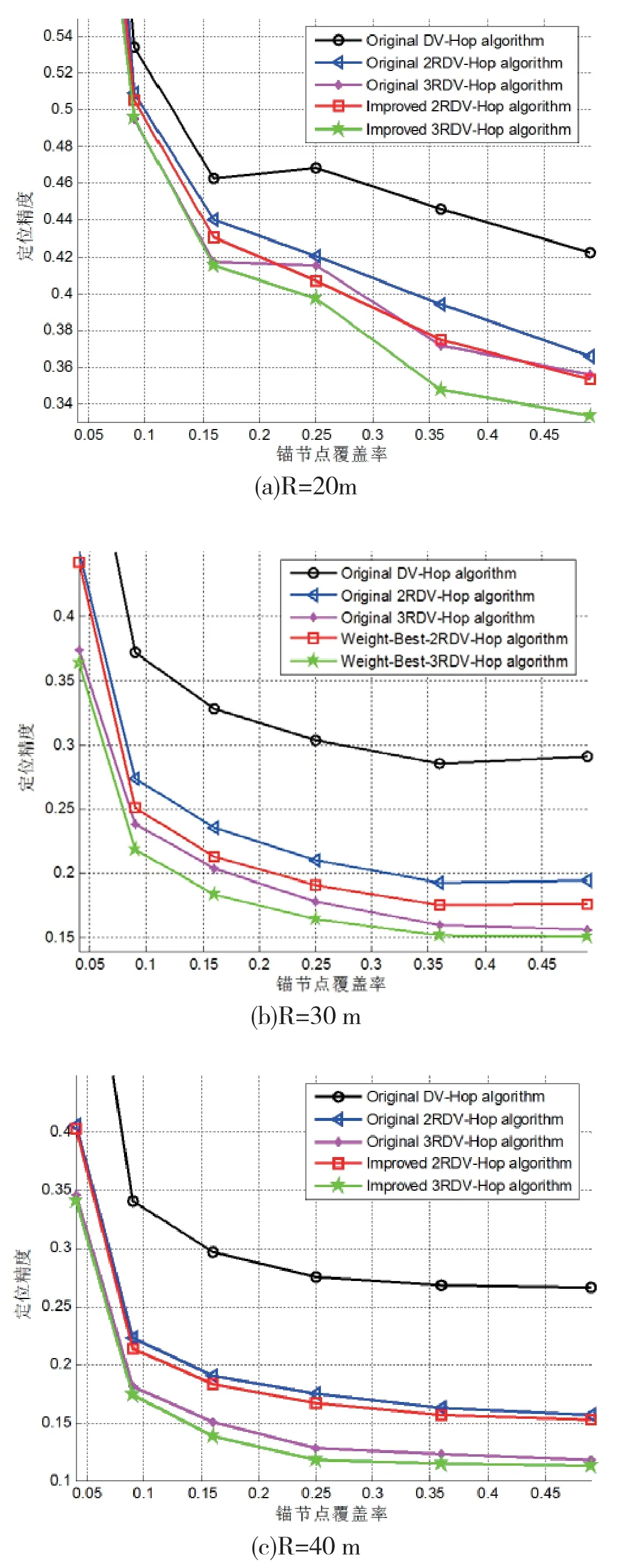
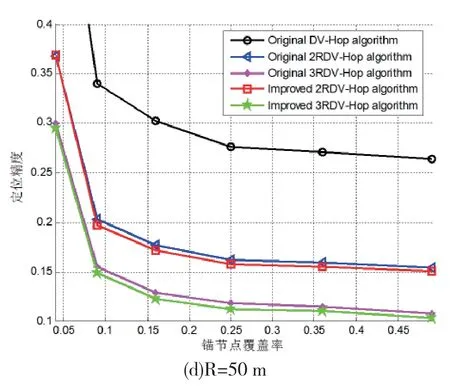
图4 五种算法对比

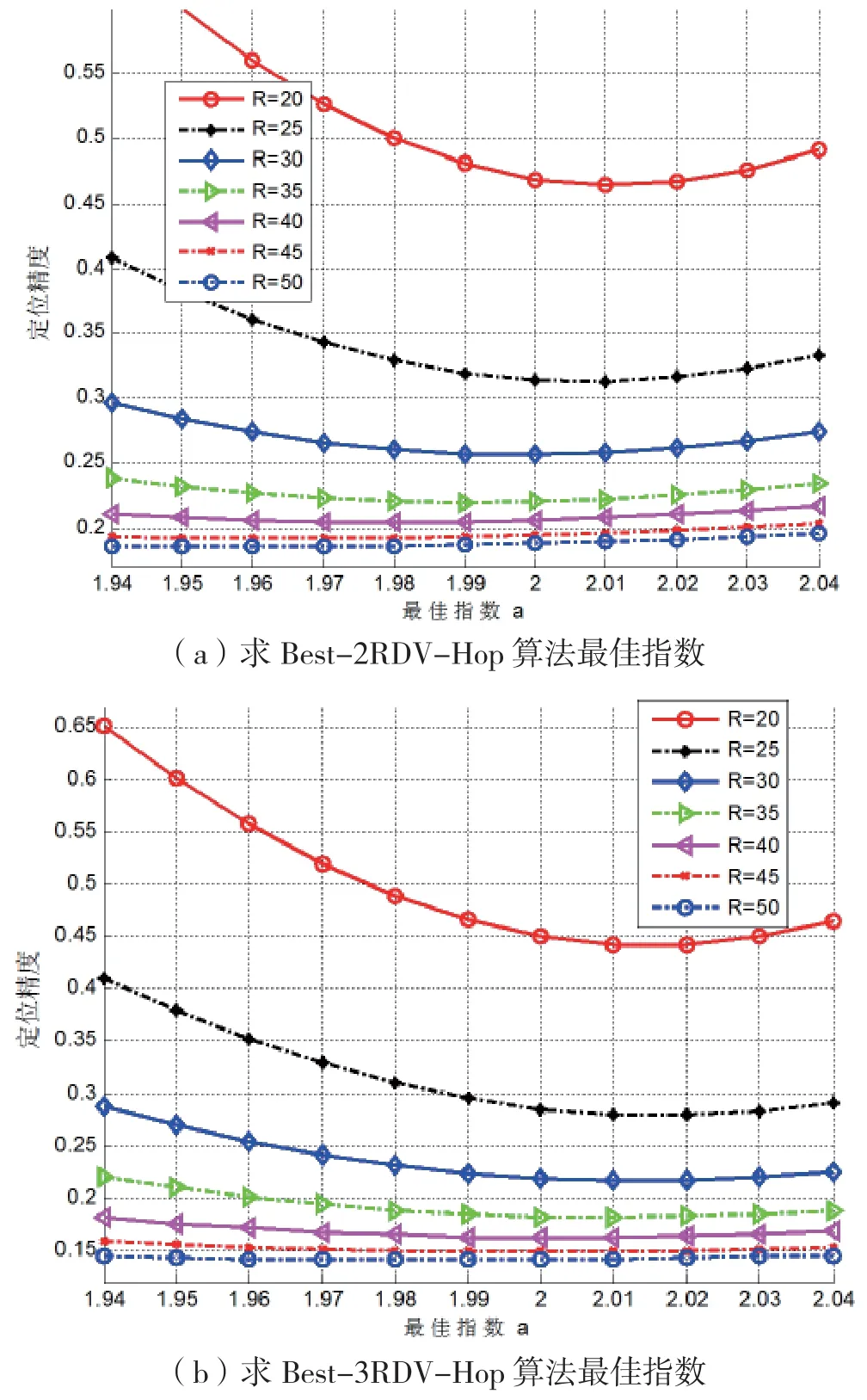
图5 求最佳指数值

在最佳指数值下，仿真本文Best-2RDVHop算法和Best-3RDV-Hop算法，并与本文2RDV-Hop算法和3RDV-Hop算法对比，结果如图6所示。

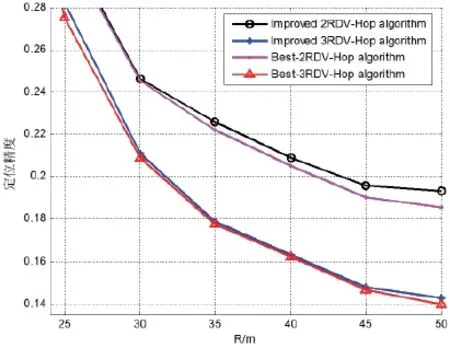
图6 本文两种算法对比

锚节点覆盖率9%、通信半径为50 m时，本文Best-2RDV-Hop算法和Best-3RDV-Hop算法分别比本文2RDV-Hop算法和3RDV-Hop算法提高定位精度约0.85%、0.35%。

3.3 Weight-Best-NRDV-Hop算法

本节仿真验证本文第三种改进算法，即性能最好的高精度最佳指数加权多通信半径DV-Hop定位算法，用Weight-Best-NRDV-Hop算法表示。

取通信半径为20、25、30、35、40、45、50 m，锚节点覆盖率9%。求Weight-Best-2RDV-Hop算法和Weight-Best-3RDV-Hop算法的最佳指数值，如图7所示。Weight-Best-2RDV-Hop算法对应的通信半径最佳指数分别为2.01、2.00、1.99、1.98、1.97、1.95、1.93。Weight-Best-3RDV-Hop算法对应的通信半径最佳指数分别为2.02、2.01、2.01、2.00、2.00、1.98、1.97。

在最佳指数值下，仿真本文Weight-Best-2RDV-Hop算法和Weight-Best-3RDV-Hop算法，并与本文Best-2RDV-Hop算法和Best-3RDV-Hop算法对比，结果如图8所示。

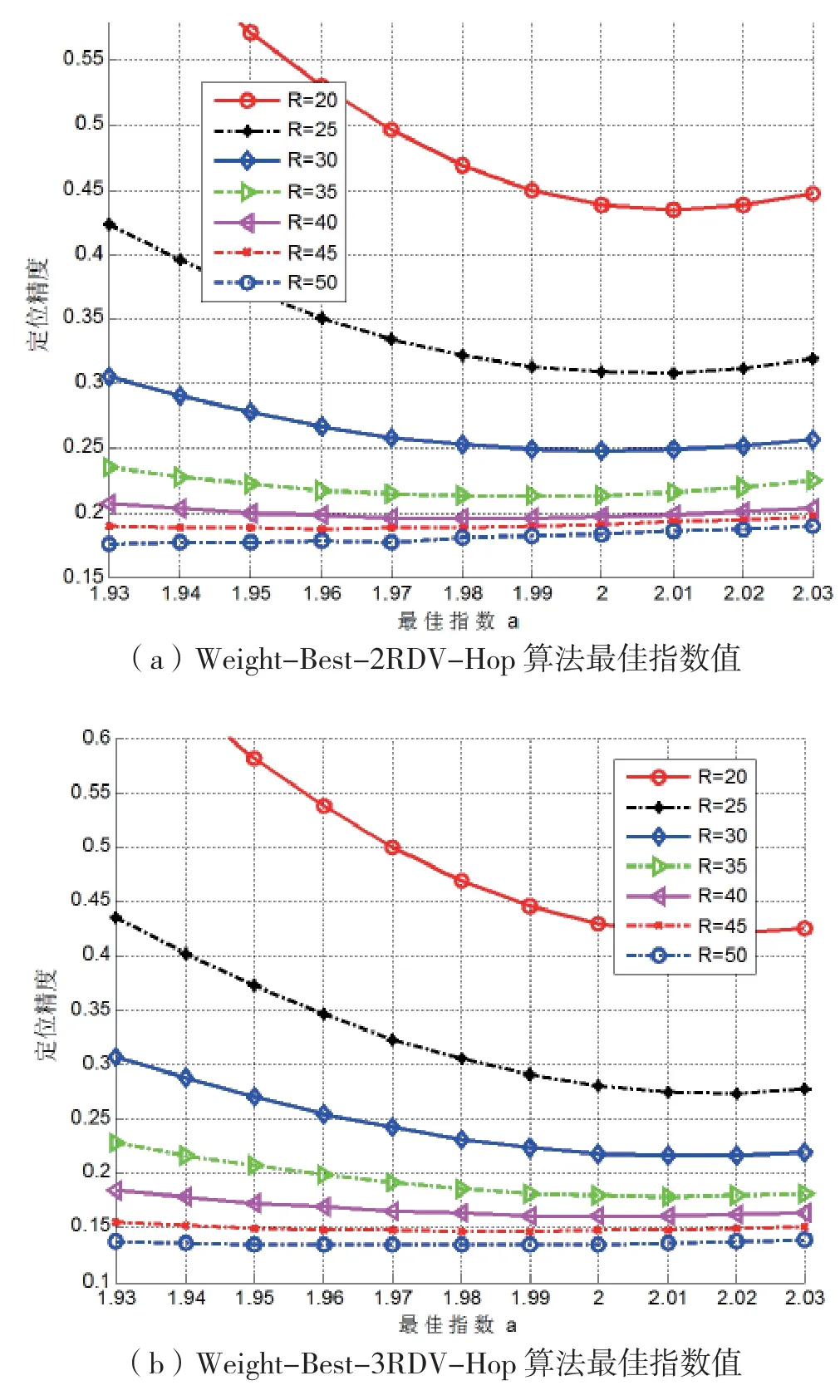
图7 求最佳指数值

图8 两种算法对比

锚节点覆盖率9%、通信半径为30 m时，本文Best-2RDV-Hop算法和Best-3RDV-Hop算法分别比本文2RDV-Hop算法和3RDV-Hop算法提高定位精度约0.81%、0.33%。

3.4 不同通信半径和锚节点覆盖率下，2、3通信半径的本文算法

取不同的通信半径和锚节点覆盖率，仿真本文Weight-Best-2RDV-Hop算 法 和Weight-Best-3RDV-Hop算法，并与DV-Hop算法（用original DV-Hop algorithm表示）、文献[18]双通信半径算法（用original 2RDV-Hop algorithm表示）、文献[18]方法下的三通信半径算法（用original 3RDV-Hop algorithm表示）对比，结果依次如图9（a）、图9（b）、图9（c）、图9（d）所示。

在不同锚节点覆盖率和通信半径下，本文Weight-Best-2RDV-Hop算法、Weight-Best-3RDVHop算法比其他算法占优势。通信半径为30 m、锚节点覆盖率为16%时，本文Weight-Best-2RDVHop算法和Weight-Best-3RDV-Hop算法比DVHop算法分别提高定位精度10.53%、13.94%，本文Weight-Best-2RDV-Hop算法比一般2RDV-Hop算法定位精度提高1.87%。本文Weight-Best-3RDVHop算法比一般3DV-Hop算法定位精度提高1.78%。

3.5 通信半径越多，定位精度越高

为研究本文Weight-Best-NRDV-Hop算法的定位规律与锚节点拥有的通信半径个数（N）的关系，取N为2,3,4,5,6，仿真定位规律。锚节点覆盖率16%，通信半径取值20～50，结果如图10所示。

通信半径N的个数越多，Weight-Best-NRDVHop算法的定位精度越高。锚节点的通信半径个数越多，网络节点泛洪次数越多节点能耗越大。

本文定位算法能大大提高节点定位精度，减小定位误差。通信半径40 m、锚节点覆盖率16%时，如图11所示，四种算法平均定位误差分别为11.9 m、5.9 m、4.7 m、3.4 m。本文Weight-Best-2RDV-Hop、Weight-Best-3RDV-Hop、Weight-Best-6RDV-Hop分别比Original DV-Hop algorithm减小定位误差6 m、7.2 m、8.5 m。所以，本文改进的无需测距DV-Hop算法能够应用在一些高精度定位中。

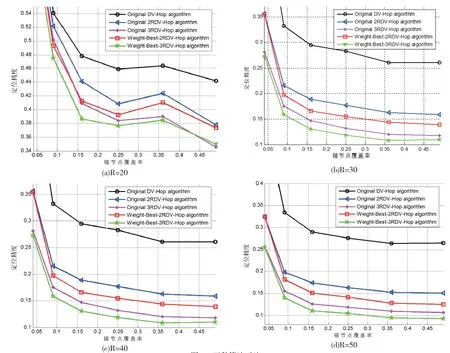
图9 五种算法对比

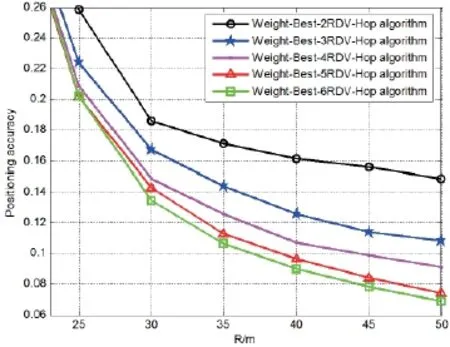
图10 不同通信半径下算法对比

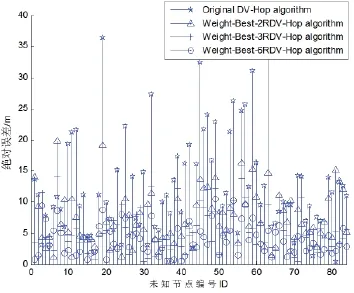
图11 四种算法对比

4 结 语

本文首先对DV-Hop算法及其改进算法进行定位误差分析，然后提出了三种高精度多通信半径DV-Hop定位算法。第一种是改进一般多通信半径的DV-Hop。第二种是在第一种改进算法基础上，改进锚节点求平均媒体跳距离的公式。第三种方法是对未知节点的校正值加权，并以前两种方法为基础。实验阶段，仿真证明三种改进的算法大大提升了DV-Hop算法的定位精度。第三种改进算法在一定条件下比DV-Hop算法能提高约23.5%的定位精度，将无需测距定位算法的定位误差限定在3 m以内。

[1] WU Hua-rui,GAO Rong-hua.An Improved Method of DV-Hop Localization Algorithm[J]. J o u r n a l o f C o m p u t a t i o n a l I n f o r m a t i o n Systems,2011,7(07):2293-2298.

[2] JIANG Ming,LI Yun-fei,GE Yuan.An Advanced DV-hop Localization Algorithm in Wireless Sensor Network[J].International Journal of Control and Automation,2015,8(03):405-422.

[3] HU Yu,LI Xue-mei.An Improvement of DV-Hop Localization Algorithm for Wireless Sensor Networks[J]. Telecommun Systems,2013,53(01):13-18.

[4] 嵇玮玮,刘中.DV-Hop定位算法在随机传感器网络中的应用研究[J].电子与信息学报,2008,30(04):970-974. JI Wei-wei,LIU Zhong.Study on the Application of DV-Hop Localization Algorithms to Random Sensor Networks[J].Journal of Electronics & Information Technology,2008,30(04):970-974.

[5] GUI Lin-qing,Thierry Val,Anne Wei.Improvement of Range-free Localization Technology By A Novel DV-hop Protocol in Wireless Sensor Networks [J].Ad Hoc Networks,2015,24(Part B):55-73.

[6] CHEN Hong-yang,Kaoru Sezaki,DENG Ping,et. al.An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks[C].International Conference on Wireless Communications Networking and Mobile Computing,2010,9(06):2232-2236.

[7] WANG Bang,WU Guang,WANG Shu,Laurence T.Yang. Localization Based on Adaptive Regulated Neighborhood Distance for Wireless Sensor Networks With A General Radio Propagation Model [J].Sensors Journal,2014,14(11):3754-3762.

[8] D. Niculescu,B. Nath.DV Based Positioning in Ad Hoc Networks[J].Journal of Telecommunication Systems,2003,22(14):267-280. D Niculescu,B Nath.Ad-Hoc Positioning System(APS)[J].IEEE Global Telecommunicatio ns,2001,5(06):2926-2931.

[9] NJculescu D,Nath B.Ad Hoc Positioning System(APS) Using AoA[C].San Franciso:IEEE INFOCOM,2003(03):1734-1743.

[10] DING Jian-ning,ZHANG Li,CHENG Guanggui,et. al.Study on DV-Hop Algorithm Based on Modifying Hop Count for Wireless Sensor Networks[J]. IJCSET,2012,2(10):1452-1456.

[11] WANG Guo,JUAN Wei.Optimization Research of the DV-Hop Localization Algorithm[J].Telkomnia Indonesian Journal of Electrical Engineering,2014,12(04):2735-2742.

[12] QIAN Qing-ji,SHEN Xuan-jing,CHEN Haipeng. An Improved Node Localization Algorithm Based on DV-Hop for Wireless Sensor Networks[J]. ComSIS,2011,8(04):953-972.

[13] Fawzi Yassine,Haidar Safa.A Hybrid DV-Hop for Localization in Large Scale Wireless Sensor Networks[C]. International Conference on Mobile Technology,New York:ACM,2009:1-6.

[14] Shrawan Kumar,D. K. Lobiyal.An Advanced DV-Hop Localization Algorithm for Wireless Sensor Networks[J]. Wireless Personal Communications An International Journal,2015,57(02):1365-1385.

[15] WU Ling-fei,Max Q.H. Meng,DONG Zhen-zhong,LIANG Hua-wei.An Empirical Study of DV-Hop Localization Algorithm in Random Sensor Networks[C].International Conference on Intelligent Computation Technology and Automation Washington,USA,DC,2009(04):41-44.

[16] 刘士兴,黄俊杰,刘宏银等.基于多通信半径的加权DV-Hop定位算法[J].传感技术学报,2015,28(06):883-887. LIU Shi-xing,HUANG Jun-jie,LIU Hong-yin,et. al.An Improving DV-Hop Algorithm Based on Multi Communication Radius[J].CHINESE JOURNAL OF SENSORS AND ACTUATORS,2015,28(06):883-887.

[17] 李娟,刘禹,钱志鸿.基于双通信半径的传感器网DV-Hop定位算法[J].吉林大学学报:工学版,2014,44(02)：502-507. LI Juan,LIU Yu,QIAN Zhi-hong.Improved DV-Hop Localization Algorithm Based on Two Communication Ranges for Wireless Sensor Network[J].Journal of Jilin University(Engineering and Technology Edition),2014,44(02):502-507.

[18] 魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法[J].西安交通大学学报,2014,48(06):1-6. WEI Quan-rui,LIU Jun,HAN Jiu-qiang.An Improved DV-hop Node Localization Algorithm Based on Unbiased Estimation for Wireless Sensor Networks[J].Journal Of Xi'an Jiaotong Unibersity,2014,48(06):1-6.

[19] 赵建平,马淑丽.基于双通信半径的DV-Hop改进算法[J].通信技术,2015,48(12):1406-1410. ZHAO Jian-ping,MA Shu-li.DV-Hop Modified Algorithm Based on Double Communication Radius[J]. Chinese Journal of Communications Technolo gy,2015,48(12):1406-1410.

[20] 马淑丽,赵建平.WSN中基于最佳指数的加权DVHop算法[J].通信技术,2015,48(10):1147-1151. MA Shu-li,ZHAO Jian-ping.Weighted DV-Hop Algorithm Based on Optimal Index in WSN[J]. Chinese Journal of Communications Technolo gy,2015,48(10):1147-1151.

[21] WANG Ying,FANG Zhiyi,CHEN Lin.A New Type of Weighted DV-Hop Algorithm Based on Correction Factor in WSNs[J].Journal of Communicatio ns,2014,9(09):699-705.

[22] Hichem Sassi,Tawfik Najeh,Noureddine Liouane. A Selective 3-Anchor DV-Hop Algorithm Based On the Nearest Anchor for Wireless Sensor Network[J]. International Scholarly and Scientific Research & Innova tion,2014,8(10):1667-1671.

孟雯雯（1990—），女，硕士研究生，主要研究方向为无线传感器网络；

赵建平（1964—），男，学士，教授，主要研究方向为无线通信技术；

马淑丽（1989—），女，硕士研究生，主要研究方向为无线传感器网络、无线通信技术。

High precision multi-communication radius Dv-hop localization algorithm

MENG Wen-wen,ZHAO Jian-ping,MA Shu-li
（College of Physics Engineering,Qufu Normal University,Qufu Shandon 273165,China）

In wireless sensor networks, DV-Hop algorithm is generally used in the low-precision positioning applications. In order to further reduce the localization error based on the DV-Ho algorithm, we put forward three kinds of high precision DV-Hop improved algorithm form three aspects based on multi communication radius. The first one, by changing the calculation of the jump numerical method, to improve the multi communication radius DV-Hop algorithm; Second, we improve the formula for calculating the average hop distance of anchor nodes based on the improved multi communication radius algorithm; Third, based on the second algorithms, the average hop distance of anchor node will be weighted, so that the size of the correction value is affected by the distance between the anchor nodes and the unknown nodes. Simulation experiments show that the improved algorithm can greatly improve the positioning accuracy of the DV-Hop algorithm.

WSN;Node localization;Multi-communication radius DV-Hop;Weighted DV-Hop

TP393

：A

：1002-0802(2016)-06-0701-10

10.3969/j.issn.1002-0802.2016.06.011

2016-02-11;

：2016-05-09 Received date:2016-02-11;Revised date:2016-05-09

国家自然科学基金资助项目（No.11404185）；山东省高等学校科技计划项目资助（No.J12LN08）；曲阜师范大学技术开发项目（No.hxkj2015017）

Foundation Item: National Natural Science Foundation of China(No.11404185); Supported by the Science and Technology Project of Higher Education of Shandong Province(No.J12LN08); Qufu Normal University Technology Development Project（No.hxkj2015017）