基于机器视觉的销钉边缘高精度定位

王章锋，孙建军

（天津工业大学 机械工程学院，天津 300387）

基于机器视觉的销钉边缘高精度定位

王章锋，孙建军

（天津工业大学 机械工程学院，天津 300387）

针对传统的高斯插值算法运用在图像检测上定位不准确，对高斯插值亚像素边缘检测算法进行了优化。首先，通过Canny算法对图像进行粗处理，再对其边缘点进行Hough变换，得到图像边缘的斜率和在插值方向的相应边缘点，通过坐标变换将梯度方向旋转至与插值方向一致；然后，对变换后的图像进行高斯插值计算。结果表明：优化后的算法能得到更高的定位精度，且具有方向不变性。将该算法运用于销钉边缘提取能满足精度要求。

高斯插值算法；图像处理；边缘高精度提取

0 引言

随着机电一体化的发展，零件大批量的生产要求不断提高。对于体积较小的销钉，限制其生产率提高的主要因素是尺寸的测量与合格品的筛选。因此，基于图像处理对销钉进行非接触检测筛选的技术研究非常重要。目前传统的边缘检测算法主要有：Robert、Sobel、Canny、Prewitt算子[1-5]这些传统算子在边缘检测过程中容易受到噪声、尺寸范围变化、灰度差异等实际情况的干扰，并且定位精度只能精确到像素级，无法满足对尺寸有较高精度要求的销钉进行精确的边缘定位[6]。为此，又提出了亚像素边缘检测算法，是基于传统边缘检测算法发展而来。在使用亚像素边缘检测算法时，常常先用传统边缘就爱内侧算法进行像素级别上的粗定位，再进一步进行更精确的定位。现有的亚像素边缘检测算法主要分为三大类：矩方法[7]，拟合法[8]，插值法[9]。传统的二次插值算法对被检边缘的方向性要求较高，方向发生变化后往往会影响插值精度，无法适应复杂的工况要求。本文通过对传统高斯亚像素插值算法进行优化来精确的提取销钉的边缘位置。实验表明，此算法应用在销钉的筛选能达到实际生产的精度要求。

销钉的生产效率很高，制约生产效率提高的一个因素就是对销钉的尺寸测量，即对销钉合格产品的筛选，而销钉本身具有多个尺寸需要测量，如图1所示。本文针对销钉的结构特征，对其边缘的定位算法进行插值方向变换优化，从而实现对销钉边缘的精确快速定位。

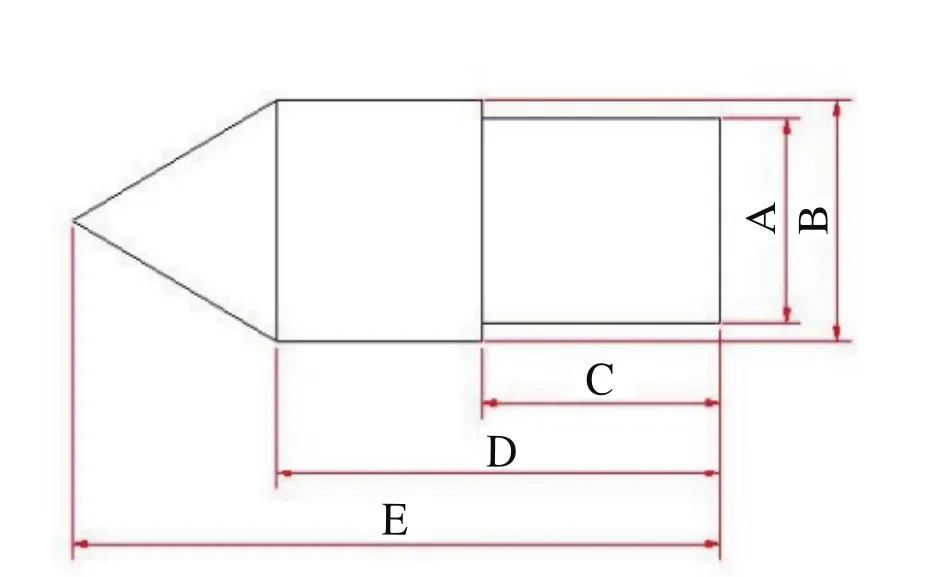
图1 销钉结构尺寸图

1 基础算法选择

由于光学元器件的卷积作用和光学衍射作用，以及光学系统的相差，导致灰度值剧变的边缘处经光学成像成为渐变式。根据方形控采样定理，在固定的时间间隔内光学元件以固定的面积对投射在其感光面上的光强进行积分，输出结果就是图像的灰度值。由于积分时间和积分面积是相对固定的，所以他的输出灰度值至于它感光面上的光强分布有关[10]。

灰度值输出表示为：

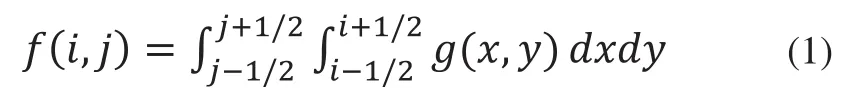
式中：f(i,j)为像素灰度值；g(x,y)为连续图像的光强分布。

实际图像边缘灰度值的分布如图2所示，可以看出阶跃边缘的变化经光学成像处理后是一个非线性的离散变化过程。对图2中所有的灰度值进行差分得到如图3所示的分布图。

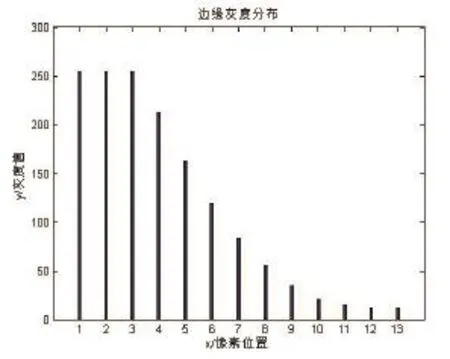
图2 边缘灰度值分布图

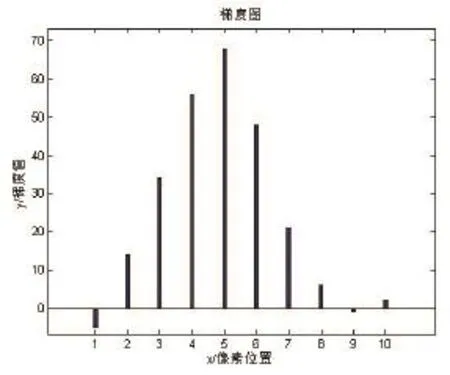
图3 边缘梯度值分布图

由上述分析可以看出，像素灰度值的输出时光学元器件上综合光强作用的结果，符合方形孔采样定理[11]。同时根据中心极限定理，从理论上讲边缘的灰度变化应当高斯分布，如图4所示，曲线的中电为边缘的精确位置。

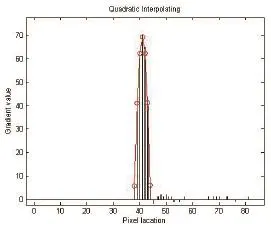
图4 边缘梯度值分布图

高斯曲线的表达式为：

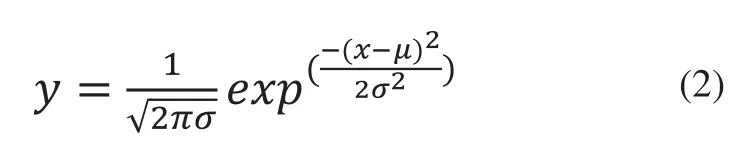
可以看出是一个典型的二次曲线，因此设方程：

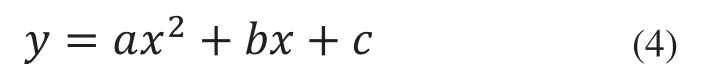
实际边缘的角度任意性，边缘灰度梯度分布不规律，较小角度的边缘灰度梯度分布无法满足插值要求，不同角度边缘的灰度值分布与灰度梯度值分布如图所示，图示小角度的边缘灰度梯度值分布并不符合插值要求。在进行二次插值过程中，式(4)只能对水平，竖直，对角线方向的梯度变化进行准确的边缘定位[7]，在实际生产过程中和图像检测领域无法实现实际边缘的检测。这一缺陷将不可避免的造成高斯插值的精度降低，无法满足实际应用当中的精度要求。因此，要对传统的高斯插值算法进行优化。

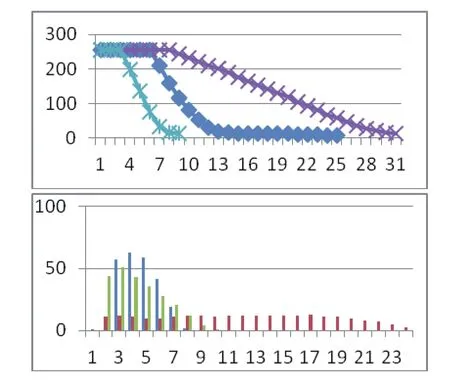
图5 不同角度边缘梯度值分布图

2 算法优化

2.1 插值方向优化

根据本课题检测对象的特征，本文将先用经典的边缘提取算法Canny算法，对图像边缘进行粗定位，对边缘线进行Hough变换[12]后从而可以对待测边缘的倾角进行初步的测量，根据实际的倾斜角度对边缘进行坐标变换，变换角度使边缘倾角更接近垂直位置，以便能得到准确的亚像素位置。

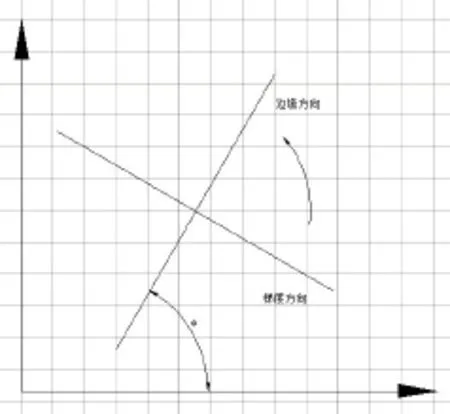
图6 沿梯度方向插值示意图

角度变换方程如下：

为了保留图像的原始灰度信息，变换过程只改变像素的坐标位置，其灰度值分布不发生变化。对变换后的图像边缘位置进行定位，定位后的精确边缘位置再经过相同的角度变换，还原至原始位置。

2.2 插值算法优化

该算法的计算精度和速度取决于插值函数的选择，综合考虑本文检测图像的特点和复杂程度，为了提高算法的运算速度，本文将传统的高斯亚像素插值定位算法进行改进，插值方程如下：

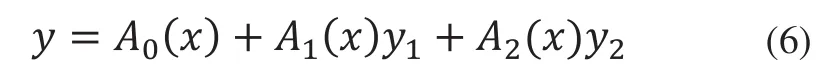
根据Hough变换后的图像边缘，提取像素点的准确坐标位置，对坐标点坐标进行式(7)～式(9)运算，可以精确的得出插值方程(6)的系数，从而根据所得二次插值函数的中心线计算公式(10)可以得出精确的边缘位置重点。

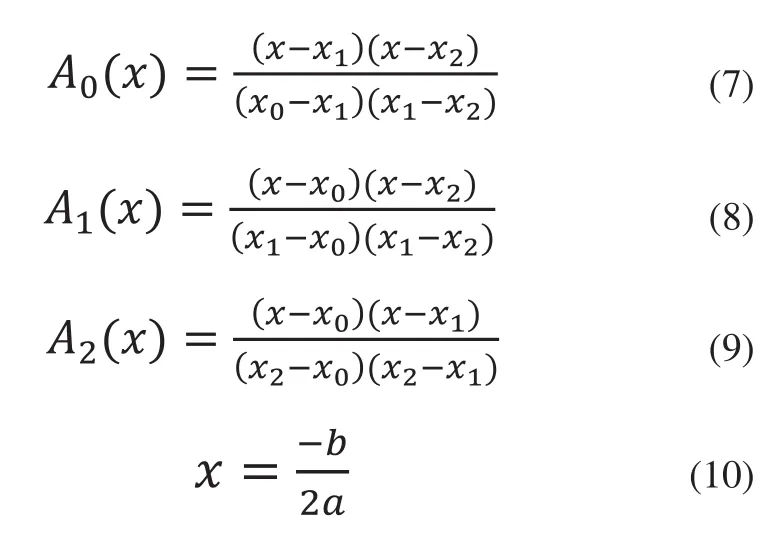
在新坐标系中经过每次插值运算的边缘点位置即为(x,y)。

3 算法验证

3.1 拟合对比试验

为了分析优化前后算法的稳定性，本算法基于MATLAB语言编写环境，分别对10°、21°、40°倾斜直线进行检测。

根据对角度测量的准确性，来判断对边缘直线定位的精准程度。

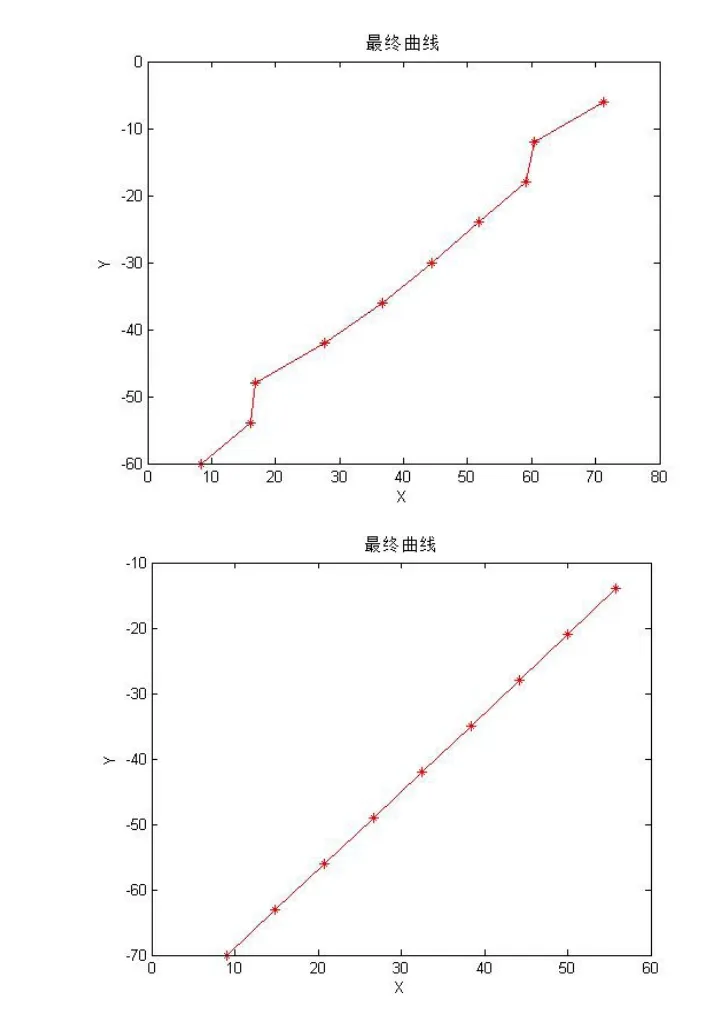
图7 优化前后相同角度直线选取

3.2 角度测量实验

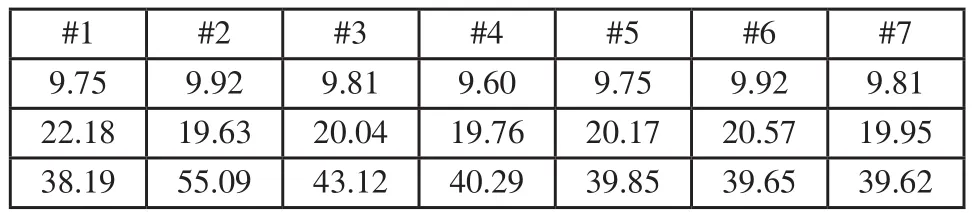
表1 原始插值方法角度检测结果

表2 优化后插值方法角度检测结果

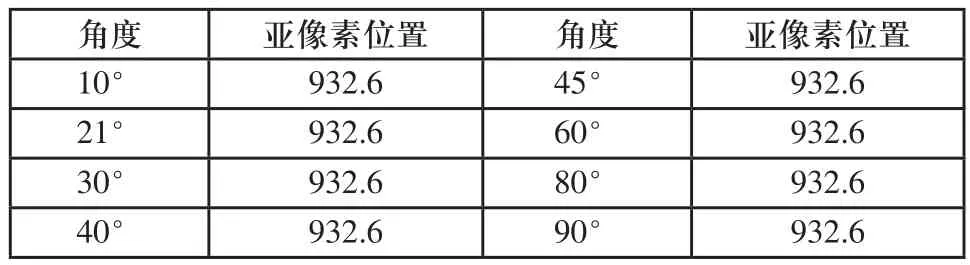
表3 不同角度直线得到的亚像素值

【】【】

根据不同倾斜角度直线的角度测试结果，表1、表2数据可以说明优化后算法在针对小角度倾斜直线测量时有更好的稳定性，而且随着角度的变换，表3数据可以说明亚像素检测精度没有发生明显的变化，因此本算法不会因检测角度的不同而影响检测精度。

根据本课题的销钉轮廓特征，优化后算法能够准确的确定直线位置，计算得到的直线位置误差在销钉的公差带要求之内，因此本算法在销钉的外轮廓尺寸测量中能够符合生产要求。

4 结论

针对销钉的外轮廓特征，通过改变高斯亚像素插值算法的插值方向，将该算法在MATLAB编译环境下对销钉图像进行验证，实验结果表明能精确的定位销钉轮廓的边缘线，可检测精度达到0.06个像素，检测精度高。该算法运在刀具尺寸检测、钢材表面缺陷、钢管内径尺寸检测等，可以实现高精度的边缘定位和尺寸测量。

[1] 赵芳,栾晓明,孙越.数字图像几种边缘检测算子检测比较分析[J].通信与信息处理,2009,28(3):68-72.

[2] 王植,贺赛先.一种基于Canny理论的自适应边缘检测方法[J].中国图象图形学报.2004,9(8):957-962.

[3] Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence.1986.

[4] O. R.Vincent,O.Folorunso.A Descriptive Algorithm for Sobel Image Edge Detection[A].Proceedings of Informing Science & IT Education Conference (InSITE)[C].2009.

[5] FRANK Y S,CHENG S.Extracting faces and facial features from color images[J].International Journal of Pattern Recognition and Artificial Intelligence.2008.

[6] Rafael C.Gonzalez,Richard E. Woods, Steven L. Eddins. Digital Image Processing Using MATLAB[M].2nd Edition.

[7] 凌远焕,徐杜,将永平,等.基于局部区域灰度矩图像边缘定位方法的研究[J].光学与光电技术,2009,7(3):60-63.

[8] 许光,明吴昭,周春兰,等.基于视觉的零件尺寸测量[J].工业控制计算机,2015,28(4):111-113.

[9] 祁晓玲,赵霞霞,靳伍银.基于机器视觉的轴类零件几何尺寸测量[J].组合机床与自动化加工技术,2013(01):65-73.

[10] 来跃深,陈琛,田军委,程钢.高斯插值亚像素边缘检测算法的优化[J].西安工业大学学报,2012(10):811-816.

[11] 吕继武,于伟,郑伟.一种基于改进的HOUGH变换的车轮检测方法[J/OL].电子技术与软件工程,2014(13).

High precision edge extraction of pin base on machine vision

WANG Zhang-feng, SUN Jian-jun

TP3-0

A

1009-0134(2016)12-0023-04

2016-08-07

王章锋（1991 -），男，河北人，硕士，研究方向为机器视觉。