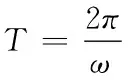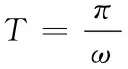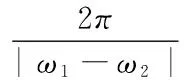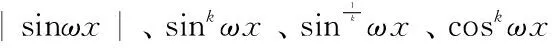最小公倍数法求最小正周期适用定理探索
陈洁,韩光松
(1.湖北工业大学理学院,湖北 武汉 430068;2.华中科技大学,湖北 武汉 430074)
最小公倍数法求最小正周期适用定理探索
陈洁1,韩光松2
(1.湖北工业大学理学院,湖北 武汉 430068;2.华中科技大学,湖北 武汉 430074)
本文主要针对最小公倍数法求和函数周期时存在的不足,基于周期函数的傅里叶级数展开式,分析了最小公倍数法求最小正周期时的不足,给出了最小公倍数法的适用定理;然后,从频谱数的角度给出了两个推论,并讨论了三种正余弦函数的周期。
最小公倍数法;最小正周期;傅里叶级数
1 引言
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)叫做周期函数,非零常数T叫做这个函数的周期。对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。常见的求解函数最小正周期的方法有定义法、公式法、图像法、检验法、求导法[1]、积分法[2]等。
当函数为多个函数和的形式时,最小公倍数法已经被大家广泛地采用,然而,文献[3-5]通过反例指出了最小公倍数法求出的周期不一定是最小正周期。到目前为止,还没有资料清楚地阐述最小公倍数法的适用条件。本文通过周期函数的傅里叶级数展开式详细地讨论了最小公倍数法的适用条件,给出了两个判据。
2 三个引理
引理1[6]设f(x)和g(x)为定义在实数域上的任意两个连续且非常值的周期函数,T1和T2分别为它们的最小正周期,则f(x)+g(x)为周期函数的充要条件是T1/T2为有理数。

3 最小公倍数法适用定理
三角函数y=Asin(ωx+φ)+k的周期仅与角频率ω有关,下面的讨论不考虑振幅A、初相φ和参数k。另外,假设讨论的正余弦函数的角频率为有理数,根据引理1,和函数的周期存在。
定理1 设周期函数f1(x)、f2(x)的傅里叶级数展开式中各正余弦函数的周期集合分别为A、B,f1(x)与f2(x)傅里叶级数展开式的和式中各正余弦函数周期的集合为C,记G{·}表示集合的最小公倍数,则 G{A∪B}≥G{C}
当且仅当等号成立时最小公倍数法适用于求和函数的周期。
证明:设周期函数f1(x)和f2(x)满足收敛定理,其周期分别为T1=2l1和T2=2l2,其傅里叶级数展开式为
根据引理2
求周期函数f1(x)与f2(x)的和时,分下面两种情况:
(1)傅里叶级数没有出现“角频率消失”现象,根据引理2,f1(x)+f2(x)的周期为
故G{A∪B}=G{C},因此,可以使用最小公倍数法。
(2)傅里叶级数出现“角频率消失”现象,不妨设存在pi和qi(i=1,2,…,r),使得
api+cqi=0,bpi+dqi=0,qil1=pil2
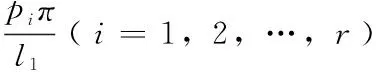
G{C}=G{A∪B-D}≤G{A∪B}=G{T1,T2}
因此,使用最小公倍数法求得的周期可能大于实际的最小正周期,当且仅当等号成立时最小公倍数法适用于求和函数的周期。
适用定理需要求周期函数的傅里叶级数,应用不是很方便,为此,根据周期函数傅里叶级数展开式中角频率数量的不同,将周期函数分为无限频周期函数和有限频周期函数,基于上面的适用定理,给出下面两个推论。
推论1 设f1(x)和f2(x)均为无限频或有限频周期函数,f1(x)+f2(x)可能出现“角频率消失”,导致G{C} 推论2 设f1(x)为无限频周期函数,f2(x)为有限频周期函数,即使f1(x)+f2(x)时出现“角频率消失”,由于该现象仅发生在有限的角频率点,仍有G(A∪B)=G(C),可以使用最小公倍数法。 为方便大家使用最小公倍数法适用定理,给出常见的无限频周期函数和有限频周期函数。 无限频周期函数 有限频周期函数 基于最小公倍数法适用定理,下面讨论三种常用正余弦函数的周期。 (1)复合函数的周期 结论:当f(x)为连续偶函数时,函数f(sinωx)+f(cosωx)中存在“角频率消失”。 (2)求f(x)=sinω1xsinω2x、sinω1xcosω2x或cosω1xcosω2x的周期,其中ω1>0和ω2>0。 由积化和差公式有 由最小公倍数法有下面的结论: 这种情况较为复杂,为简单起见,这里通过一个例题进行说明。 例1 求f(x)=sin43xcos5x的最小正周期。 解 存在常数ci(i=0,1,2),使得sin43x=c0+c1cos6x+c2cos12x,于是 f(x)=c0cos5x+c1cos6xcos5x+c2cos12xcos5x [1] 李世杰.周期函数和周期数列[M].浙江大学出版社,2008,7. [2] 李和逊.用定积分给出函数周期的一种方法[J].重庆职业技术学院学报,2002,1. [3] 孙亦器.关于两周期函数之和的最小正周期问题[J].中学数学月刊,2005,2. [4] 韦存军,封云.用最小公倍数法求周期函数的周期[J].中学数学杂志,2006,1. [5] 朱威军.从两道错题谈周期函数[J].科技资讯,2011,17. [6] 张严选.论任二周期函数和差积商的周期性[J].江苏广播电视大学学报,1997,2. 陈洁(1976-),女,湖北工业大学理学院,博士,讲师。 韩光松(1984-),男,华中科技大学,博士。 G623.5 A 1671-1602(2016)22-0229-024 正余弦函数的周期